양자화(신호처리)

양자화(quantization)는 수학 및 디지털 신호 처리에서 큰 집합(종종 연속 집합)의 입력 값을 종종 유한한 수의 요소를 가진 작은 집합의 출력 값으로 매핑하는 과정입니다.반올림 및 절단은 양자화 프로세스의 전형적인 예입니다.디지털 형태로 신호를 표현하는 과정은 일반적으로 반올림을 포함하므로 양자화는 거의 모든 디지털 신호 처리에서 어느 정도 관여한다.양자화는 기본적으로 모든 손실 압축 알고리즘의 핵심을 형성합니다.

입력값과 그 양자화된 값의 차이(반올림 오류 등)를 양자화 오류라고 합니다.양자화를 실행하는 장치 또는 알고리즘 함수를 양자화기라고 합니다.아날로그-디지털 변환기는 양자화기의 한 예입니다.

예

예를 들어, $실수{\displaystyle }$x(\$style$ x$)$를 가장 가까운 정수 값으로 반올림하면 매우 기본적인 유형의 정량자(균일한 수량자)가 형성됩니다.양자화 스텝사이즈가 일부 값$\delta {\displaystyle \mathrm{}}$(\$displaystyle\Delta)$와 동일한 전형적인 (중간 판독) 균일한 양자화기는 다음과 같이 나타낼 수 있습니다.

$=$$$$델타 }}+{\frac {1}{2}}\right\rfloor$

여기서 표기법 $"\displaystyle\lfloor\loor"$는 바닥의 기능을 나타냅니다.

양자화기의 기본 속성은 가능한 출력 값 멤버의 카운터블 세트가 가능한 입력 값 집합보다 작다는 것입니다.출력값 집합의 멤버는 정수, 유리 또는 실제 값을 가질 수 있습니다.가장 가까운 정수로 단순 반올림할 경우 스텝사이즈$\delta {\displaystyle \mathrm{}}$(\$displaystyle \Delta$})는$$ 1입니다.$\delta {\displaystyle \mathrm{}}$ ${\displaystyle =}$ {$displaystyle \Delta =1}$ 또는$$$\delta {\displaystyle \mathrm{}}$ {$displaystyle \Delta$}이$$(가) 다른 정수 값과 같으면 이 양자화기에는 실수 값 입력과 정수 값 출력이 있습니다.

그 양자화 단계 크기(Δ)은 신호에 변화가 양자화되는 것에 비해서는 상대적으로가 평균 제곱 오차 그런 사용하면 반올림 연산에 의해 생산된 약 2/12{\displaystyle\Delta ^{2}/12}Δ 걸 보여 주는 것 .[1][2][3][4][5][6]제곱 오차도 양자화 nois라고 불린다 평균은 간단하다.e파워이다.양자화기에 1비트를 더하면 δ의 값이 반감되어 노이즈 파워가 계수 δ만큼 감소한다.데시벨의 경우 노이즈 파워의 변화는 ${\displaystyle {\mathrm{10\mu log}}_{}}$ ${\displaystyle \mathrm{10\mu }(}$1${\displaystyle }$/${\displaystyle 4\mathrm{}}$ ${\displaystyle \text{)≈}}$ - ${\displaystyle \mathrm{6dB}}$입니다$.{$ $displaystyle \script style$ 10 \ $cdot$\ $log$ _ { $10$ ($1$ /$4$ ) $\ about$ \$6$\ $mathrm${$dB$} } 。

양자화기의 가능한 출력값의 세트는 계수 가능하기 때문에, 양자화기는 분류 단계(또는 전진 양자화 단계)와 재구성 단계(또는 역 양자화 단계)라고 불릴 수 있는 2개의 별개의 단계로 분해할 수 있다.이 단계에서 입력값을 정수 양자화 단계에 매핑한다.인덱스 $(\displaystyle$ k$)$ 및$$ 재구성 단계는 $인덱스{\displaystyle }$k(\$displaystyle$ k$)$를 입력 값의 출력 근사치인 재구성 $값{\displaystyle {}_{}}$ $(\$})에$$ 매핑합니다.위에서 설명한 균일한 양자화 예에서 순방향 양자화 단계는 다음과 같이 표현될 수 있다.

$displaystyle$$$$델타 }}+{\frac {1}{2}}\right\rfloor$

그리고 이 예제 양자화기의 재구성 단계는 단순합니다.

${\displaystyle y_{}}$ k ${\displaystyle {}_{}}$ ${\displaystyle k}$ ${\displaystyle \cdot }$ ${\displaystyle \mathrm{\delta }}$ display$$（ \ $displaystyle$ y$_$ { k } $= k$ \ $cdot$\$Delta$ $\}$ ） 。

이 분해는 양자화 동작의 설계 및 분석에 유용하며, 양자화된 데이터가 통신 채널을 통해 어떻게 전달될 수 있는지를 보여줍니다. 소스 인코더는 전진 양자화 단계를 수행하고 통신 채널을 통해 인덱스 정보를 전송할 수 있으며, 디코더는 재구성 단계를 수행할 수 있습니다.원래 입력 데이터의 출력 근사치를 생성합니다.일반적으로 순양자화 단계는 입력 데이터를 양자화 지표 데이터의 정수 공간에 매핑하는 함수를 사용할 수 있으며, 역양자화 단계는 개념적으로(또는 문자 그대로) 각 양자화 지수를 대응하는 재구성 값에 매핑하는 테이블 룩업 연산일 수 있다.이 2단계 분해는 벡터 및 스칼라 양자화에도 동일하게 적용됩니다.

수학적 특성

양자화는 다대소 매핑이기 때문에 본질적으로 비선형이며 되돌릴 수 없는 프로세스입니다(즉, 동일한 출력값이 여러 입력값으로 공유되기 때문에 일반적으로 출력값만 주어졌을 때 정확한 입력값을 회복하는 것은 불가능합니다).

가능한 입력값의 집합은 무한히 클 수 있으며 연속적일 수 있으며 따라서 셀 수 없습니다(모든 실수의 집합이나 제한된 범위 내의 모든 실수의 집합 등).가능한 출력 값 집합은 유한하거나 셀 수 있을 정도로 무한할 ^[6]수 있습니다.양자화와 관련된 입력 및 출력 세트는 비교적 일반적인 방법으로 정의할 수 있습니다.예를 들어, 벡터 양자화는 다차원(벡터 값) 입력 ^[7]데이터에 양자화를 적용하는 것입니다.

종류들

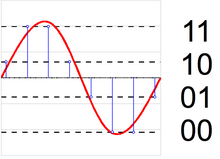
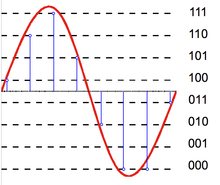
아날로그-디지털 변환기

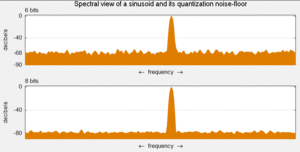
아날로그-디지털 변환기(ADC)는 샘플링과 양자화의 두 가지 프로세스로 모델링할 수 있습니다.샘플링은 시간 가변 전압 신호를 일련의 실수의 이산 시간 신호로 변환합니다.양자화는 각 실수를 유한한 이산값 집합의 근사치로 대체한다.일반적으로 이러한 이산 값은 고정 소수점 단어로 표시됩니다.임의의 수의 양자화 레벨이 가능하지만 공통 워드 길이는 8비트(256레벨), 16비트(65,536레벨) 및 24비트(1,680만레벨)입니다.숫자의 시퀀스를 양자화하면 양자화 오류 시퀀스가 생성되며, 확률적 동작 때문에 양자화 노이즈라고 불리는 가산 랜덤 신호로 모델링되기도 합니다.양자화기가 사용하는 레벨이 많을수록 양자화 노이즈 파워는 낮아집니다.

환율 왜곡 최적화

레이트 왜곡 최적화 양자화는 손실 데이터 압축 알고리즘의 소스 코딩에서 발생합니다.이 알고리즘의 목적은 통신 채널 또는 기억 매체에 의해 지원되는 비트환율 한도 내에서 왜곡을 관리하는 것입니다.이 맥락에서 양자화 분석에는 양자화기의 출력을 나타내기 위해 사용되는 데이터 양(일반적으로 자릿수, 비트 또는 비트환율로 측정됨)과 양자화 프로세스에 의해 발생하는 정밀도 손실(왜곡이라고 함)이 포함됩니다.

미드라이저 및 미드트레드 균일한 양자화기

서명된 입력 데이터에 대한 대부분의 균일한 양자화기는 미드라이저와 미드트레드의 두 가지 유형 중 하나로 분류할 수 있습니다.이 용어는 값 0 주위의 영역에서 발생하는 현상을 기반으로 하며, 계량기의 입출력 함수를 계단으로 보는 것과 유사합니다.미드트레드 양자화기는 제로값 재구성 레벨(계단의 트레드에 대응)을 가지며, 미드라이저 양자화기는 제로값 분류 임계값(^[9]계단의 라이저에 대응)을 가진다.

미드트레드 양자화에는 반올림이 포함됩니다.미드트레드 균일한 양자화 공식은 이전 섹션에서 설명합니다.

미드라이저 양자화에는 절단이 포함됩니다.미드라이저 균일한 양자화기의 입출력 공식은 다음과 같습니다.

$x$$$$델타 }}\$right$\rfloor +{\frac {1}{2}}\right$

분류규칙이 주어지는

$\displaystyle k=\left\lfloor\frac {x}{\델타 }}\right\rfloor}$

재건 규칙은

${\displaystyle y_{}}$ k $=$ ${\displaystyle \mathrm{\delta }}$ k ${\displaystyle （k}$ + ${\displaystyle \frac{1}{}}$ 2$$）{ $displaystyle y_{k$}=\$Delta \cdot \left(k+{\tfrac$ {$1}{2}}\right$

미드라이저 균일한 양자화기에는 0 출력 값이 없습니다. 즉, 최소 출력 크기는 스텝 크기의 절반입니다.반면 미드트레드 양자화기의 출력 레벨은 제로입니다.일부 애플리케이션에서는 제로 출력 신호 표현이 필요할 수 있습니다.

일반적으로 미드라이저 또는 미드트레드 양자화기는 실제로 균일한 양자화기가 아닐 수 있습니다. 즉, 양자화기의 분류 간격의 크기가 모두 동일하지 않거나 가능한 출력 값 사이의 간격이 모두 동일하지 않을 수 있습니다.미드라이저 양자화기의 구별되는 특징은 정확히 0인 분류 임계값을 갖는다는 것이며 미드스레드 양자화기의 구별되는 특징은 정확히 ^[9]0인 재구성 값을 갖는다는 것이다.

데드존 양자화기

데드존 양자화기는 대칭 동작이 0에 가까운 미드 스레드 양자화기의 한 종류입니다.이러한 양자화기의 제로 출력값 주위의 영역을 데드존 또는 데드밴드라고 부릅니다.데드존은 때때로 노이즈 게이트 또는 스켈치 기능과 같은 용도로 사용될 수 있습니다.특히 압축 어플리케이션의 경우 데드존에는 다른 스텝의 폭과 다른 폭이 주어질 수 있습니다.그렇지 않으면 균일한 양자화기의 경우 정방향 양자화^[10][11][12] 규칙을 사용하여 데드존 폭을 임의의$값{\displaystyle }$(\$displaystyle$ w$)$으로 설정할 수 있습니다.

${\displaystyle k}$ ${\displaystyle =}$ ${\displaystyle \mathrm{sgn}}$ ${\displaystyle (}$ (${\displaystyle x}$ ) ${\displaystyle \cdot max}$ ( ${\displaystyle 0\mathrm{}}$, ${\displaystyle \lfloor \frac{x}{}}$ -${\displaystyle \frac{w}{}}$ / ${\displaystyle \frac{2\mathrm{}}{}\frac{\mathrm{}}{}}$ + ${\displaystyle 1}$ ${\displaystyle \rfloor }$ ) {$displaystyle$ k = \$operatorname {sgn}(x$) \ $cdot \$max \$left$ ( $0$, \$lfloor$ \ $frac$\$frac$ { \ $left x$\ $right$- w / 2 } { \ $delta }$ + 1 \$light$ \$$$loor$ )

${\displaystyle \mathrm{여기}}$서 함수$$sgn $\displaystyle$ \$operatorname$ {sgn$\}$ ( )은 기호 함수(일명$$기호 함수)입니다.이러한 데드존 양자화기에 대한 일반적인 재구성 규칙은 다음과 같다.

${\displaystyle y_{}}$ k ${\displaystyle {}_{}}$ ${\displaystyle \mathrm{sgn}}$ (${\displaystyle k}$ )${\displaystyle w\frac{}{}}$ ( ${\displaystyle \frac{\mathrm{w}}{}}$2 + k${\displaystyle k}$ ${\displaystyle 、}$ ${\displaystyle \mathrm{k}}$- $1$ +${\displaystyle {}_{}{r}_{}}$k ) { $displaystyle$y _ { k } = \$operatorname${ $sgn$ } ($k$ ) \ $cdot$\ leftw\$frac${$w$} + \$Delta$ \$cdot$ ( $k$- 1 + r _ k \ r _ r _ k \ r _ k )$$$}$ ) ,

${\displaystyle {여기}_{}}$서 r k$(\$는 스텝크기의 분수로 0 ~1 범위의 재구성 오프셋 값입니다.일반적으로 0 주위에 대칭이고 0에서 피크 값에 도달하는 일반적인 확률 밀도 함수(PDF)를 사용하여 입력 데이터를 양자화할 때 0${\displaystyle {}_{}}$ r ${\displaystyle k_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \frac{1}{}}$ 2 ${\$ 0$\leq r_{k}\leq {tfrac {1}{2}}}$입니다.${\displaystyle r_{}}$ k$(\$는 일반적으로 k$(\displaystyle$ k$)$에 의존하며, 아래에 설명된 최적 조건을 충족하기 위해 선택할 수 $있지만{\displaystyle {}_{}}$, 대부분의 경우 ${\displaystyle \frac{\mathrm{단순히}}{}}$ 1 2$(\displaystyle {1}{$2$\}\})$와 같이 상수로 설정됩니다(이 ${\displaystyle {정의}_{}}$에서는 y $=$ ${\displaystyle 0}$(\$displaystyle y_0})$ 만기 t$).$o ${\displaystyle \mathrm{sgn}}$\$displaystyle \operatorname {sgn$ $함수$의 정의이므로 r 0 ${\$은(는) ${\displaystyle {영향}_{}}$을 받지 않습니다.)

매우 일반적으로 사용되는 특수한 경우(예: 재무회계 및 초등수학에 일반적으로 사용되는 체계)는 $모든{\displaystyle }$ k$\backslash$$style$ k에 대해$$w ${\displaystyle =}$= \ $displaystyle$ w = \ $Delta }$ 및$$ ${\displaystyle r_{}}$ k ${\displaystyle {}_{}}$ ${\displaystyle \frac{1}{}}$ \ 2$$\ \ $displaystyle r_{k$} =$displaytfrac {1}{2}}}$를 $설정$하는 것입니다. 이 경우, 데드존도 정량화됩니다.이 양자화기의 중앙 정지 구역은 다른 모든 단계와 동일한 너비를 가지며 모든 재구성 값도 동일한 간격입니다.

노이즈 및 오류 특성

선택 첨가 소음 모델

양자화 오류 분석의 일반적인 가정은 부가 백색 노이즈와 유사한 방식으로 신호 처리 시스템에 영향을 미친다는 것이다. 즉, 신호와 거의 상관관계가 없고 전력 스펙트럼 ^{[2][6][13][14]}밀도가 거의 평평하다.가산 노이즈 모델은 디지털 필터링 시스템의 양자화 오차 효과 분석에 일반적으로 사용되며, 이러한 분석에서 매우 유용할 수 있습니다.부드러운 PDF로 ^[2][15]고해상도 양자화(신호 강도에 비해 작은$\delta {\displaystyle \mathrm{}}$ \$displaystyle \Delta ）$의 경우 유효한 모델인 것으로 나타났습니다.

추가 소음 거동이 항상 유효한 가정은 아니다.양자화 오류(여기서 설명한 바와 같이 양자화 오류)는 결정적으로 신호와 관련이 있으며 신호와는 완전히 독립적이지 않습니다.따라서 주기적인 신호는 주기적인 양자화 노이즈를 발생시킬 수 있습니다.또한 경우에 따라서는 디지털 신호 처리 시스템에 한계 사이클이 나타날 수도 있습니다.양자화 오류로부터 효과적으로 독립할 수 있는 한 가지 방법은 양자화 ^[6][14]전에 신호에 랜덤(또는 의사 랜덤) 노이즈를 추가하는 디더화(노이즈 쉐이핑에 의한 경우도 있습니다)를 실행하는 것입니다.

양자화 오류 모델

일반적인 경우 원래 신호는 1개의 LSB(List Significant Bit)보다 훨씬 큽니다.이 경우 양자화 오차는 신호와 큰 상관관계가 없으며 분포가 거의 균일합니다.양자화에 반올림을 사용하는 경우 양자화 오차의 평균은 0이고 루트 평균 제곱(RMS) 값은 이 분포의 표준 편차이며, 1 ${\displaystyle \frac{}{}\mathrm{}}$ ${\displaystyle \mathrm{L}}$ S ${\displaystyle \mathrm{B}}$0.${\displaystyle 289\mathrm{}}$ ${\displaystyle \mathrm{L}}$ S ${\displaystyle \mathrm{B}}$ \ $displaystyle$\ script style \ $frac {1}{\sqrt {12}}\ mathrm {LSB$ \ } \ \ $0{\displaystyle \frac{\mathrm{}}{}}$. $28$ 。e error의 평균은 ${\displaystyle \mathrm{0}}$이 $.\$$mathrm {LSB$}. RMS 값은 ${\displaystyle \frac{\sqrt{1\mathrm{}}}{}}$ ${\displaystyle \mathrm{3L}}$ ${\displaystyle \mathrm{S}}$B(\$displaystyle \scriptstyle \frac {1}{\sqrt$ {3$\}\}\})$입니다. 단, 반올림 오류는 RMS보다 작습니다.${\displaystyle \frac{}{}2\mathrm{}}$ ${\displaystyle \mathrm{L}}$ S ${\displaystyle \mathrm{B}}$\ $displaystyle$\$script$style \ $frac {1$} {$LSB$ $AC$ 오류의 RMS 값은 두 경우 모두 동일하기 때문에 오류의 DC 용어를 무시할 수 있는 상황(AC 결합 시스템 등)에서 절단을 반올림하는 특별한 이점은 없습니다.어느 경우든 양자화 비트수의 1비트 변화마다 전체 신호 범위의 백분율인 표준 편차는 2배로 변화합니다.따라서 잠재적인 신호 대 양자화/노이즈 전력비는 4 또는 ${\displaystyle {\mathrm{10\mu }}_{}}$ ${\displaystyle {\log }_{}}$ ${\displaystyle \mathrm{10\mu }(}$4$)\$ 10$\cdot \log$ _${10}(4$비트당 약 6dB)만큼 변경됩니다.

낮은 진폭에서는 양자화 오차가 입력 신호에 의존하게 되어 왜곡이 발생합니다.이 왜곡은 안티에일리어싱 필터 후에 생성되며, 이러한 왜곡이 샘플링 레이트의 1/2을 넘으면 대상 대역에 에일리어스됩니다.입력 신호로부터 양자화 오차를 독립시키기 위해서, 신호에 노이즈를 부가해 신호를 디코딩 한다.이것에 의해, 신호 대 노이즈비가 약간 감소합니다만, 왜곡을 완전하게 해소할 수 있습니다.

Quantization 소음 모델

양자화 노이즈는 ADC의 양자화에 의해 도입된 양자화 오류 모델입니다.ADC에 대한 아날로그 입력 전압과 출력 디지털 값 사이의 반올림 오류입니다.노이즈는 비선형이며 신호에 의존합니다.여러 가지 다른 방법으로 모델링할 수 있습니다.

양자화 오차가 -1/2 LSB와 +1/2 LSB 사이에서 균일하게 분포하고 신호가 모든 양자화 레벨을 포함하는 균일한 분포를 갖는 이상적인 ADC에서는 Signal-to-Quantization-Noise Ratio(SQNR; 신호 대 양자화 잡음비)는 다음과 같이 계산할 수 있다.

$\displaystyle \mathrm {SQNR} = 20\log _{10}(2^{Q})\약 6.02\cdot Q\\mathrm {dB} \,\!}$

여기서 Q는 양자화 비트 수입니다.

이를 충족하는 가장 일반적인 테스트 신호는 전폭 삼각파와 톱니파입니다.

예를 들어 16비트 ADC의 최대 신호 대 양자화 노이즈비는 6.02 × 16 = 96.3 dB입니다.

입력 신호가 최대 진폭 사인파일 경우 신호의 분포가 더 이상 균일하지 않으며 대신 해당 방정식이 다음과 같습니다.

$\displaystyle \mathrm {SQNR} \약 1.761+6.02\cdot Q\\mathrm {dB} \,\!}$

여기서 양자화 노이즈는 다시 균등하게 분포되어 있다고 가정한다.입력 신호가 높은 진폭과 넓은 주파수 스펙트럼을 갖는 경우입니다.^[16]이 경우 16비트 ADC의 최대 신호 대 잡음비는 98.09dB입니다.신호 대 잡음의 1.761 차이는 신호가 삼각형이나 톱니가 아닌 풀 스케일 사인파이기 때문에만 발생합니다.

고해상도 ADC의 복잡한 신호의 경우 이는 정확한 모델입니다.저해상도 ADC, 고해상도 ADC의 저레벨 신호, 단순 파형의 경우 양자화 노이즈가 균일하게 분포되지 않아 이 모델이 부정확합니다.^[17]이러한 경우 양자화 노이즈 분포는 신호의 정확한 진폭에 의해 크게 영향을 받습니다.

계산은 풀스케일 입력에 상대적입니다.신호가 작을 경우 상대 양자화 왜곡이 매우 클 수 있습니다.이 문제를 회피하기 위해 아날로그 컴팬딩을 사용할 수 있지만 왜곡이 발생할 수 있습니다.

설계.

Granular이 왜곡과 과부하 왜곡이다.

대부분의 경우 양자화 설계에서는 제한된 범위의 출력 값만 지원하고 입력이 지원되는 범위를 초과할 때마다 출력을 이 범위로 제한하는 클리핑을 수행합니다.이 클리핑에 의해 발생하는 에러는 과부하 왜곡이라고 불립니다.지지범위의 극한범위 내에서 양자화기의 선택가능한 출력값 사이의 간격량을 입도라고 하고, 이 간격에 의해 발생하는 오차를 입도왜곡이라고 한다.양자화기 설계에서는 입상 왜곡과 과부하 왜곡 사이의 적절한 균형을 결정하는 것이 일반적입니다.지원되는 출력 값의 수에 대해 평균 입도 왜곡을 줄이려면 평균 과부하 왜곡을 증가시켜야 하며 그 반대도 마찬가지입니다.신호의 진폭(또는 이에 상당하는 양자화 스텝사이즈$\delta {\displaystyle \mathrm{}}$(\$displaystyle\Delta$})을 제어하여 적절한 밸런스를 달성하는 방법은 자동 게인 제어(AGC)를 사용하는 것입니다.단, 일부 양자화 설계에서는 입상 오차 및 과부하 오차 개념이 적용되지 않을 수 있습니다(예를 들어 제한된 입력 데이터 범위 또는 셀 수 있을 정도로 무한대의 출력 ^[6]값 세트를 가진 양자화기의 경우).

Rate–distortion quantizer 디자인

양자화 연산을 실행하는 스칼라 양자화기는 일반적으로 다음 두 단계로 분해할 수 있습니다.

분류

M ${\displaystyle -}$ 1$$$({displaystyle$ M${\displaystyle {}_{}{}_{}^{}}$} k ${\displaystyle {=}_{}^{}}$ ${\displaystyle 1_{}}$({$displaystyle \{k}\}_{k=1}^{M$의 결정값을${\displaystyle {정의}_{}}$하여 ${\displaystyle {입력신호}_{}^{}}$ 범위를 ${\displaystyle {\mathrm{M}}_{}^{}}$({$displaystyle$M} k${\displaystyle {}_{}{}_{}^{}}$${\displaystyle {=}_{}^{}}$ ${\displaystyle {\mathrm{M}}_{}^{}}$ - 1$$- {$b_{$displaystyle$\}){\displaystyle }$의 ${\displaystyle {\mathrm{비연속구간}}_{}^{}}$으로 $분류$하는 프로세스입니다.${\displaystyle [}$ ${\displaystyle {}_k}$ -${\displaystyle {}_{}\text{1}{}_{}}$, ${\displaystyle b_{}}$k $)$ (k ${\displaystyle =}$ 1,${\displaystyle 2}$, ${\displaystyle ...}$ , ${\displaystyle M}$ $(\display$ k ${\displaystyle {}_{}}$ 1, 2$,$ $\ldots , M$)의 경우(${\displaystyle {최대\mathrm{}}_{}}$ $한계$는${\displaystyle }$b 0 = - ${\displaystyle \mathrm{=}}$ -$${\ \ $display$ { $k$$$} = [ $b _$$${ k - 1$$$}$ ~ ~$b$ ${\displaystyle {\_}_{}}$ {$$k } ) ${\displaystyle {}_{}}$ [ b _ { k _ { $k$ } } } 。val $range{\displaystyle {}_{}}$ ${\displaystyle I_{}}$ k$(\$I_${k$})는$$ 동일한 양자화 $인덱스{\displaystyle }$k(\$displaystyle$ k$)$와 관련되어 있습니다.

재구축

Each interval ${\displaystyle I_{k}}$ is represented by a reconstruction value ${\displaystyle y_{k}}$ which implements the mapping ${\displaystyle x\in I_{k}\Rightarrow y=y_{k}}$.

이 두 단계는 모두 y ${\displaystyle =Q}$ (${\displaystyle x}$) {$displaystyle$ y$=Q(x$의 $수학적{\displaystyle }$ 연산을 구성합니다.

엔트로피 부호화 기술은 분류 단계를 실행하는 소스 인코더에서 재구성 단계를 실행하는 디코더로 양자화 지수를 통신하기 위해 적용될 수 있다.이를 위한 한 가지 방법은 각 양자화 $인덱스{\displaystyle }$k$(\$ k$)$를 바이너리 코드워드 $c(\displaystyle c_$${\displaystyle {}_{}}$k})에 관련짓는 것입니다.${\displaystyle \mathrm{여기}}$서 l e n ${\displaystyle \mathrm{g}}$ t h(\$displaystyle \mathrm {length}(c_{k$로 나타내는 각 코드워드에 사용되는 비트수를 고려해야 합니다.그 ${\displaystyle \mathrm{결과}}$ M의 $설계$입니다.${\displaystyle }${\$displaystyle$ M$}$ 수준$$ 정량자 및 인덱스 값을 전달하기 위한 관련 코드워드 집합은 {${\displaystyle b_{}}$ k ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle {}_{}^{}}$M -$$ {$style$\ {$b_{k}_{k=1}$ ${M-1$${\displaystyle }${${\displaystyle c_{}}$ ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ $1$M {$displaystyle \{c_{k$} {k} = {k} {k} = {k} {k}${\displaystyle }${k}의 값을 찾아야 합니다$.$$=1$}{M$$$}:$ $비트레이트{\displaystyle }$ $R(\displaystyle$ R$$$)$ 및 $왜곡{\displaystyle }$ D$(\displaystyle$ D$)$와 같은 선택된 설계 제약 조건을 최적으로 충족합니다$.$

$정보원{\displaystyle }$ S$(\displaystyle$ S$)$가 관련된 $PDF{\displaystyle }$ f$x)$ {$displaystyle$ f$(x$$)\}$ {$displaystyle$ X$}$를 생성한다고 가정할 때$,$ 랜덤 변수가 특정 양자화 $간격{\displaystyle {}_{}}$(\$displaystyle I_{$k$$})에 속할 ${\displaystyle {확률}_{}}$은 giv이다.입력자:

${\displaystyle p_{}}$ k ${\displaystyle {}_{}P}$ [ ${\displaystyle x{}_{}}$ I ${\displaystyle k_{}}$] ${\displaystyle ={}_{b{}_b}^{}}$ ${\displaystyle {{\mathrm{k}}_{}}_{}^{}}$ - ${\displaystyle {{}_{}}_{{}_{}}^{}}$ ${\displaystyle {{}_{}}_{}^{}k}$ f${\displaystyle }$( x ) $d x$[ x \ $display style$ p _ { $k$} = \$int _$ { k - 1 }^{ $b$_ {$k$ }$f ( x$ )$\}$

이 양자화기의 결과 비트레이트 $R($$양자화$ 값당 평균 비트 단위)은 다음과 같이 구할 수 있습니다.

${\displaystyle R}$ ${\displaystyle =}$ ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{k}}}$ ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle p_{}}$ k${\displaystyle {}_{}l\mathrm{}}$ l ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{n}}$ g ${\displaystyle \mathrm{t}}$h ( ${\displaystyle {}_{}{k}_{}}$ ) ${\displaystyle =\underset{k}{\overset{}{}}}$ k ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle \underset{}{\overset{}{1}}}$ ${\displaystyle \underset{}{\overset{}{}}\mathrm{}}$ ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{n}}$ g ${\displaystyle \mathrm{t}}$h ( ${\displaystyle {}_{}{k}_{}}$ )${\displaystyle {}_{}^{}b}$ ${\displaystyle {b_{}}_{}^{}}$k - ${\displaystyle {1_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{{}_{}}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$f (${\displaystyle x}$ ) ${\displaystyle d}$ x {$$\ $sum$ _ { $sum$_ { k =$1$}^{ $M }$p _ $k }$ \ $cdot$\ $mathrm${$$k } （ c $k$）

왜곡이 평균 제곱 ^[a]오차로 측정된다고 가정할 경우 왜곡 D는 다음과 같습니다.

${\displaystyle D}$ ${\displaystyle =E}$[ (${\displaystyle x}$ -${\displaystyle Q}$ (${\displaystyle {x\mathrm{}}^{}}$ )${\displaystyle {}^{}}$2 ${\displaystyle ={}_{}^{}}$- -${\displaystyle {\mathrm{}}_{}^{}}$Q${\displaystyle }$(${\displaystyle }$x${\displaystyle {}^{}}$)${\displaystyle {}^{}}$f (${\displaystyle }$x )${\displaystyle d}$ x ${\displaystyle =}$ ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{k}}{{}_{}}_{}^{}\underset{}{\overset{}{=}}}$ ${\displaystyle \underset{}{\overset{}{1}}}$ ${\displaystyle {M_{}}_{}^{}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}^{}}$ ${\displaystyle {{}_{}}_{{}_{}}^{}}$- ${\displaystyle {}_{}}$ ${\displaystyle b_{}}$ k ( x - y${\displaystyle {}_{}{}^{}}$k )${\displaystyle {}^{}}$f (${\displaystyle }$x )${\displaystyle d}$x ( ${\displaystyle x}$ ) d x ( x ) _ { $displaystyle$ D =$E$( x -$$ ( x ) \ $int$ ) _ 2 }^$2$

주요 관찰 결과, $속도{\displaystyle }$R$({displaystyle$ R$$})은${\displaystyle {결정}_{}}$ ${\displaystyle {\mathrm{경계}}_{}^{}}${${\displaystyle b_{}^{}}$ k${\displaystyle {}_{}{}_{}^{}}$} ${\displaystyle {\mathrm{k}}_{}^{}}$ ${\displaystyle {=}_{}^{}}$ 1 M - 1$({b_{k}\}$${\displaystyle {\_}_{}^{}}$${k=1}^{M-1})$ 및 코드워드 길이${\displaystyle }${$l$ ${\displaystyle \mathrm{e}}$ n ${\displaystyle \mathrm{g}}$ ${\displaystyle \mathrm{h}(c_{}}$)${\displaystyle {}_{=}^{}}$ ${\displaystyle {}_{}^{}}$M({$displaystyle \{k})$에 따라 달라진다.} 결정$$${\displaystyle {}_{}}$ {${\displaystyle b_{}}$} k${\displaystyle {}_{}^{}}$= ${\displaystyle {\mathrm{M}}_{}^{}}$- 1 { displaystyle \ {$b_{$k}$_{k=1}^{M-1$$}$ 및 재구성${\displaystyle {}_{}}$ {${\displaystyle y_{}}$k${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle {\mathrm{k}}_{}^{}}$= ${\displaystyle {}_{}^{}}$ $M${ displaystyle \ {$y_{k}\}_{k=1$}^{M$\}$에 따라 달라집니다$.$

양자화기의 이들2가지 퍼포먼스메트릭을 정의한 후 양자화기 설계 문제의 일반적인 레이트 왜곡 공식은 다음 두 가지 방법 중 하나로 나타낼 수 있습니다.

1. 최대 왜곡 $제약{\displaystyle }$ D${\displaystyle }$† ${\displaystyle D_{}}$max {\$displaystyle$D\$leq$D_{\max$\}\}$을 지정하면 $비트레이트{\displaystyle }$ R ${\displaystyle$ R$}$을 최소화합니다.
2. 최대 비트 레이트 $제약{\displaystyle }$ R${\displaystyle r_{}}$ R$max$ { \ $displaystyle$R \ $leq$ R$_$ { \ max$\}\}$ 를 지정하면 $왜곡{\displaystyle }$D { \ $displaystyle$ D$$} 를 최소화합니다.

대부분의 경우 이러한 문제에 대한 해법은 제약이 없는 ${\displaystyle 문제}$ min ${\displaystyle \{D}$ +${\displaystyle r}$ R$}({displaystyle \min$ \left$\{D+\$$lambda$ $\cdot$ R$\right$$\})$로 변환하여 동등하게($또는$ 대략적으로) 표현하고 해결할 수 있습니다.여기서 Lagrange 승수는 음이 아닌 $정수$입니다$.$그는 속도와 왜곡 사이의 적절한 균형을 잡는다.구속되지 않은 문제를 해결하는 것은 문제의 등가 제약된 공식에 대한 해군의 볼록 껍질에서 점을 찾는 것과 같습니다.단, 이 세 가지 문제 중 하나에 대한 해결책(특히 폐쇄형 솔루션)을 찾는 것은 어려울 수 있습니다.다차원 반복 최적화 기법이 필요하지 않은 솔루션은 ^[18]균일한 분포, ^[12]지수 분포 및 라플라시안^[12] 분포의 3가지 PDF에서만 공개되었습니다.반복적인 최적화 접근방식을 사용하여 다른 ^[6][19][20]경우에 솔루션을 찾을 수 있습니다.

재구성${\displaystyle }$값 {${\displaystyle y_{}}$ k ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle 1_{}^{}}$({$displaystyle$\{$y_{k}\}_{k=1}^{M})$은 왜곡에만 영향을 미칩니다.$또{\displaystyle {}_{}}$, 각 y k(\$displaystyle$ $y_$${k})$는 다음과 같이 총 왜곡에 대해 개별적으로 ${\displaystyle {기여}_{}}$합니다$.$

${\displaystyle D=\sum _{k=1}^{M}d_{k}$

어디에

${\displaystyle d_{k}=\int _{b_{k-1}^{b_{k}}(x-y_{k})^2}f(x)f(x)cap}$

${\displaystyle {}_{}}$ 관찰을 통해 {b ${\displaystyle k_{}}$ ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle 1_{}^{}}$ -$$ { { $displaystyle$\ {$b$$$_ { k $} _$ { $k$$$$= 1$} { k$$= 1 } { k }$m$ ${\displaystyle {the}_{}}$ the the the the the the the the 、 \ $display d$} $の$ of of this separ separ this this separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ separ

평균 제곱 오차 왜곡 기준에서는 각 구간 K $i_${$display$ $style$ $i_$${k}$의 재구성 값 $y{\displaystyle {}_{}}$를 {\${\displaystyle {}_{}^{}}$ \{$y_{k}^*}\}_{k=$1}^{$M$$}$로 설정하면 최적의 재구성${\displaystyle }$값 세트 {$y$ k ${\displaystyle {}_{}^{}{}_{}^{}}$} k $=$ 1 M이 제공됨을 $쉽게$ 알 수 있다.구간 내 이온성 기대치(중심이라고도 함)는 다음과 같습니다.

${\displaystyle {}_{}^{}\frac{{}_{}}{}}$ k ${\displaystyle {}_{}^{}}$ = ${\displaystyle \frac{1_{}}{}}$ ${\displaystyle {p{}_{}}_{}^{}}$ k ${\displaystyle \frac{{}_{}}{}{}_{{}_{}}^{{}_{}}}$ ${\displaystyle {{\mathrm{k}}_{}}_{}^{}}$ - ${\displaystyle {1_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}k}$ x${\displaystyle f}$ ( x )${\displaystyle d}$x {\$displaystyle y_{k$}^{*} $= p_{k}}\int$_ {$b_{k-1}^{b_{k}}{x$}glac$($$x)}.$

${\displaystyle \mathrm{충분히}}$ 잘 설계된 엔트로피 부호화 기술을 사용하면 {${\displaystyle k_{}^{}}$} ${\displaystyle {\mathrm{k}}_{}^{}}$ ${\displaystyle {=}_{}^{}}$ 1$$ {\$displaystyle \{k\}_{k=1}^{$M$\}\}$ 지수의 실제 정보 내용에 가까운 비트 전송률을 사용할 수 있습니다.이렇게 함으로써 효과적으로 사용할 수 있습니다.

${\displaystyle \mathrm {length}(c_{k})\about -\log _{2}\left(p_{k}\right)}$

그렇기 때문에

${\displaystyle R}$ ${\displaystyle =\underset{k}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{\mathrm{k}}}}$ ${\displaystyle \underset{}{\overset{}{=}}{}_{}}$ M - ${\displaystyle p_{}}$ k${\displaystyle {}_{}{\log }_{}}$ ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$ ( ${\displaystyle {}_{}{k}_{}}$ $){$ $displaystyle$ R = \ $sum$_ { k$$=$1$}^{ $M$} - p$_$ { $k$} \ $cdot$\$log _$ {2} \$left$ ( $p$_ { $k$} \$right$ )$$}

이 근사치를 사용하면 엔트로피 부호화 설계 문제를 양자화기 자체의 설계에서 분리할 수 있습니다.산술 부호화와 같은 최신 엔트로피 부호화 기술은 알려진(또는 적응적으로 추정된) 확률${\displaystyle }${${\displaystyle p_{}}$ k ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle 1_{}^{}}$ $({$\{$p_{k}\}_{k=$1}^{$M$일 때 소스의 실제 엔트로피에 매우 가까운 비트 전송률을 달성할 수 있습니다.

일부 설계에서는 특정 개수의 분류 $영역{\displaystyle }$M(\$displaystyle$ M$)$에 최적화하는 것이 아니라 M$(\displaystyle$ M$)$ $값$의 최적화를 포함하는 양자화기 설계 문제가 발생할 수 있습니다.일부 확률론적 소스 모델의 경우 M$${\$displaystyle$ M$}$이(가) 무한대에 근접할 때 $최상$의 성능을 달성할 수 있습니다.

그 엔트로피 제약 조건 무시:Lloyd–Max 양자화

위의 공식에서 비트레이트 제약이$0$으로 설정됨으로써 무시되는 경우(\$displaystyle \lambda)$ 또는$$ 가변 길이 코드(또는 산술 부호화 등 기타 엔트로피 부호화 기술) 대신 양자화된 데이터를 나타내기 위해 고정 길이 코드(FLC)가 사용되는 것으로 가정되는 경우)속도 왜곡의 의미에서 FLC)를 사용하므로 최적화 문제가 D$(\style$ D$)$의 왜곡을 최소화합니다.

M$${$displaystyle$ M$}$ 레벨$$ $양자화기$에서 생성되는 인덱스는 R ${\displaystyle ={\log }_{}}$ ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle {}_{}m}$ M${\$ { $display$ R = \ $lceil$\ $log$ _ ${$2$}$M\rceil$$$$} bits/display를 $사용$하여 고정 길이 코드를 사용하여 코드화할 수 있습니다.예를 들어 M $=$ {$displaystyle$ M=} 256레벨인 $경우{\displaystyle }$ FLC $비트레이트{\displaystyle }$R {\$displaystyle$ R$}$은 8비트/140입니다.이러한 이유로 이러한 양자화기를 8비트 양자화기라고 부르기도 합니다.그러나 FLC를 사용하면 더 나은 엔트로피 부호화를 사용하여 얻을 수 있는 압축 개선 효과가 제거됩니다.

M$(\displaystyle$ M$)$ 수준의$$ $FLC$를 가정하면 환율 왜곡 최소화 문제를 왜곡 최소화만으로 줄일 수 있습니다.감소된 문제는 다음과 같습니다. PDF $)$의 $소스$$$X {\$displaystyle$ X$}$ {{displaystyle f$$($x)}$ {{$displaystyle$ f(x)} {\$displaystyle$f(x)} ${\$displaystyle f(x)} {\displaystyle f(x)} {{$b} =$={$k}$ ={$1}$의 결정${\displaystyle }$경계를 찾아야 합니다.e구성 수준 { ${\displaystyle {}_{}}$ k ${\displaystyle {}_{}{}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {=}_{}^{}}$ ${\displaystyle {}_{}^{}}$M { $displaystyle$\ { y$_$ { $k$} \ }$_$ { $k = 1$}^{ M } $e$ dist e dist e e e e e e $。{\displaystyle }$왜곡의 발생을 최소화할 수 있습니다.

$1$$\}.$

한 quantizer은 가끔 MMSQE(최소 mean-square 양자화 오차)해결책, 그리고 결과PDF-optimized(불균등)quantizer에 Lloyd–Max quantizer 개별의 두세트를 해결하기 위해 반복 methods[6][21][22]두개 사람의 이름을 딴으로 명칭은 위의 문제 결과에 최적의 솔루션 찾기. simultaneou$s$ 공식은${\displaystyle \mathrm{}}$follows${\displaystyle }$D / ${\displaystyle \partial \mathrm{}}$ ${\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\displaystyle {}_{}}$ { $displaystyle$ \ displaystyle \ $display$ D / \ $partial$ b$_$ { k } ${\displaystyle =}$ $0$ { $display$ d /${\displaystyle \mathrm{}{k}_{}}$ y ${\displaystyle \mathrm{k}}$ $=$ 0 { style \$display$ D / \ $partial$ y$_$ { k} =$0$ s s resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting $resulting$ resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting resulting

${\displaystyle \frac{d}{}}$ D${\displaystyle \frac{\mathrm{}{b}_{}}{}}$ b k${\displaystyle \frac{{}_{}}{}}$= ${\displaystyle 0b_{}}$ b ${\displaystyle \frac{{}_{}}{}{}_{}}$=${\displaystyle \frac{{}_{}{y}_{}}{}}$ k +${\displaystyle \frac{y_{}}{}}$ ${\displaystyle \frac{{\mathrm{k}}_{}}{}}$ +$$ 2 （$displaystyle$）$$= 0 \ $rightarrow b$_ { k } = {$y$_ { k } +$y _${ $k$+ $1$} \$over$2 ）${\displaystyle \frac{\mathrm{}}{}}$、

각 재구성 값 쌍 사이의 중간 지점에 각 임계값을 배치합니다.

$({displaystyle\displayD \over \rightarrow y_{k}=0\rightarrow y_{k}={b_{k-1}^b_{k})_int \over \int _{b_{k-1}^{b_{k}{k})_int(x)_int.$

각 재구성 값을 관련 분류 간격의 중심(조건부 기대치)에 배치합니다.

1957년에 처음 기술된 Lloyd의 Method I 알고리즘은 데이터를 벡터링하는 어플리케이션에서 쉽게 일반화할 수 있습니다.이 일반화에는 Linde-Buzo-Gray(LBG) 또는 k-평균 분류기 최적화 방법이 있습니다.게다가 벡터 ^[23]데이터에 대한 엔트로피 제약도 포함하도록, 한층 더 알기 쉬운 방법으로 일반화할 수 있다.

균일한 양자화 및 6dB/bit 근사치

${\displaystyle {}_{}}$ 양자화기는 입력 PDF가 [y ${\displaystyle {1\mathrm{}}_{}}$-${\displaystyle \mathrm{\Omega }}$ /${\displaystyle \text{2}{}_{}}$, ${\displaystyle y_{}}$M +${\displaystyle \mathrm{\Omega }}$ / $](\display$ [$y_{$1} - \$Delta /$ 2, $~y_${M} +\$Delta$/ 2$))$ 범위에 걸쳐 균일하게 분포되어 있는 경우 실제로는 균일한 양자화기입니다.단, 그러한 최소 분포는 없습니다.균등하게 분포된 선원에 적용되는 균일한 양자화기의 분석은 다음과 같이 요약할 수 있습니다.

$대칭{\displaystyle }$ 소스 X는${\displaystyle }$x${\displaystyle [}$[ - ${\displaystyle X_{}}$max , ${\displaystyle X_{}}$max $]$ \ $display style$x \ $in$[ - ${\displaystyle {}_{}}$ $_$\ $max$ , $X _$ { \ $max }$ $=1$ ${\displaystyle \frac{{}_{}}{}}$ X$$ {$2 X _$ { \ $max }$ }$$, $f{\displaystyle }$$$ 0 0 0 f f f f elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere elsewhere a a a a a a a a a a a a a a a a a스텝 사이즈 ${\displaystyle \delta \frac{\mathrm{}}{}}$ ${\displaystyle =}$ 2 ${\displaystyle \frac{X_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ M$${\$displaystyle \Delta$= t $tfrac${ $2X_{\max }}{M}}$ 및$$ 양자화 잡음비(SQNR)는 다음과 같습니다.

${\displaystyle \mathrm{S}}$ ${\displaystyle \mathrm{Q}}$ ${\displaystyle \mathrm{N}}$ R ${\displaystyle =}$ ${\displaystyle {\mathrm{10}}_{}}$ ${\displaystyle {\log }_{}}$ 10 ${\displaystyle {}_{}}$ ${\displaystyle \frac{{\mathrm{}}_{}^{}}{}}$ 2 ${\displaystyle \frac{{\mathrm{}}_{}^{}}{}}$ 2${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle {\mathrm{10}}_{}}$ ${\displaystyle {\log }_{}}$ 10${\displaystyle \frac{m}{}{}_{}}$（ M${\displaystyle \frac{{}^{\delta \mathrm{}}}{}}$ )${\displaystyle \frac{{}^{}}{}}$2 / ${\displaystyle \frac{12}{}}$ ${\displaystyle 10}$ 2 / 12 ${\displaystyle {}^{}}$ ${\displaystyle {10\mathrm{}}^{}}$ ${\displaystyle {\log }_{}}$ 10 ${\displaystyle {}^{}}$ M$$ 2 =$20$ ${\displaystyle {\log }_{}}$ 10${\displaystyle {}_{}m}$ M { $style$ { SQNR$}$=$10$ \ $log$ { 10 \ log { $10 }$ { \ $fr$}{$fr$ }

N$(\displaystyle$ N$)$ 비트를$$ $사용$하는 고정 길이 코드의 $경우{\displaystyle }$ M ${\displaystyle =}$ $(\$ M=$2^{N$이 됩니다.${\displaystyle \mathrm{그}}$ 결과, ${\displaystyle \mathrm{S}}$ ${\displaystyle \mathrm{Q}}$ N ${\displaystyle \mathrm{R}}$ ${\displaystyle =}$ ${\displaystyle {20}_{}}$ log ${\displaystyle 10{\mathrm{}}^{}{}_{}\mathrm{n}}$ 2 ${\displaystyle N}$ ${\displaystyle {}^{}}$ N${\displaystyle （}$ ${\displaystyle {\mathrm{20}}_{}}$ ${\displaystyle {\log }_{}}$ 10 ${\displaystyle {}_{}}$ 2${\displaystyle }$） ${\displaystyle =}$ ${\displaystyle N}$ ${\displaystyle \cdot 6}$ .$0206$ D （ { $QRM$） ） 。$N\cdot$6.$0206,$ {\$rm {dB$

또는 비트당 약 6dB입니다.예를 들어 N$({displaystyle$ N$}$ $=$ 8비트의 $경우{\displaystyle }$ M$({displaystyle$ M$}$ $=$ 256레벨 및 SQNR = 8×6 = 48dB), N$({displaystyle$ N$}$ $=$ 16비트인 $경우{\displaystyle }$ M$({displaystyle$ M$}$ $=$ 65536 및 SQNR = 96D)입니다.양자화에 사용되는 추가 비트마다 SQNR이 6dB 개선되는 특성은 잘 알려진 장점입니다.그러나 이 파생물은 균일한 소스에 적용되는 균일한 양자화기에 대해서만 사용되므로 주의해야 합니다.다른 소스 PDF 및 기타 양자화 설계에서는 SQNR은 PDF 유형, 소스 유형, 양자화 유형 및 동작 비트환율 범위에 따라 6dB/bit로 예측되는 것과 다소 다를 수 있습니다.

단, 많은 소스에서는 충분히 높은 비트환율로 동작할 때 양자화기 SQNR 함수의 기울기를 6dB/bit로 근사할 수 있다고 가정하는 것이 일반적입니다.점근적으로 높은 비트환율에서 스텝사이즈를 반으로 자르면 샘플당 비트환율이 약 1비트씩 $증가$하며(값이 이전 더블사이즈 간격의 왼쪽 절반인지 오른쪽 절반인지를 나타내기 위해 1비트가 필요하기 때문에), δ2 / $12$에${\displaystyle {}^{}\mathrm{기초}}$하여 평균$$제곱오차를 4배(즉 6dB) 감소시킵니다.style $\Delta$^{$2}/12} 근사치$.

점근적으로 높은 비트 전송률에서는 엄격한 이론 ^[2][3][5][6]분석에 의해 많은 소스 PDF에 대해 6dB/bit 근사치가 지원됩니다.게다가 최적 스칼라 양자화기 구조(환율 왜곡의 의미)는, 이러한 ^[5][6]조건하에서 균일한 양자화기의 구조에 접근한다.

기타 분야

실제로 많은 물리량이 물리적인 실체에 의해 정량화된다.이 제한이 적용되는 분야에는 전자공학(전자 때문에), 광학(광자 때문에), 생물학(DNA 때문에), 물리학(플랑크 한계 때문에), 화학(분자 때문에) 등이 있습니다.

「 」를 참조해 주세요.

• 베타 인코더
• 색 양자화
• 데이터 비닝
• 이산화
• 디스커버리
• 포스터화
• 펄스 코드 변조
• 양분위수
• 양자화(이미지 처리)
• 회귀 희석 – 설명 변수 또는 독립 변수의 양자화와 같은 오류로 인한 모수 추정치의 편향

메모들

레퍼런스

추가 정보

• Bernard Widrow; István Kollár (2007). Quantization noise in Digital Computation, Signal Processing, and Control. ISBN 9780521886710.