섀넌-파노-엘리아스 부호화

이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : 'Shannon-Fano-Elias 코딩'– 뉴스 · 신문 · 서적 · 학자 · JSTOR (2016년 4월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인)

정보 이론에서, 섀넌-파노-엘리아스 부호화는 산술 부호화의 전조이며, 여기서 확률은 코드 워드를 ^[1]결정하기 위해 사용된다.

알고리즘 설명

부호화할 순서가 지정된 값의 이산 랜덤 변수 X가 주어지면 p${\displaystyle }$(${\displaystyle x}$) {$displaystyle$ p$(x)}$를 X 내의 임의의 x에 대한 확률로 $합니다{\displaystyle }$.함수의 정의

${\displaystyle {F}}(x)=\sum _{x_{i}<x}p(x_{i})+{\frac {1}{2}p(x)}p(x)}$

알고리즘:

각 X in X에 대해

Z를 F ${\displaystyle (}$ (${\displaystyle x}$ $){$ $displaystyle {F$$x)$의 바이너리 전개라고 합니다.

x, $L{\displaystyle }$(${\displaystyle x}$) { $displaystyle$L ($x$ )$$${\displaystyle +}$ ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle {}_{}\frac{11}{}}$p (${\displaystyle \frac{x}{}}$ )${\displaystyle \frac{}{}}$+$$ \ $displaystyle$ \$lceil$\$log$ _ { $2$} { \ $frac${ 1$$} {$p$ ( x ) } \ $right$\$rceil + 1$ } 의 부호화 길이를 선택합니다.

x, ${\displaystyle c}$ ${\displaystyle o}$ d${\displaystyle }$e (${\displaystyle x}$) \ $displaystyle$code ($x$ )$$\ $displaystyle$L ($x$)$$の choose choose after after${\displaystyle }$after after after비트를 선택합니다.

예

X = {A, B, C, D}, 확률 p = {1/3, 1/4, 1/6, 1/4}이라고 가정합니다.

A의 경우

$({displaystyle {F}}(A)=black {1}{2}}p(A)=black {1}{2}}\cdot {flac {1}{3}}=0.1666)...}$

이진법에서 Z(A) = 0.0010101010...

L(A) =${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle log\frac{\mathrm{}}{}{}_{}}$2 ${\displaystyle \frac{\frac{3}{}}{}}$ 1 1 ${\displaystyle 3}$ + 1 {$displaystyle$\ $lceil$ \ $log _$ ${$2} ${\ frac {1}$ {3$}$ } \$right$ \ $rceil$+$1$=$$ 3

코드(A)는 001입니다.

B의 경우

${\displaystyle {F}=p(A)+{\frac {1}{2}}p(B)=frac {1}{3}+{\frac {1}{4}=0.45833...}$

이진수에서 Z(B) = 0.0111010101...

L(B) $={\displaystyle }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ 1 1${\displaystyle {}_{}}$1 ${\displaystyle \frac{\frac{4}{}}{}}$ ${\displaystyle +}$ +$$ { $displaystyle \ left$\ lceil \ $log$ _ ${$2$} {\ frac {1}$ {$4}$ } \$right$ \ $rceil$+$1$=$$ 3

코드(B)는 011 입니다.

C의 경우

${\displaystyle {F}=p(A)+p(B)+{\frac {1}{3}}+{\frac {1}{4}+{\frac {1}{6}=0666...}$

이진법에서 Z(C) = 0.101010101010...

L(C) =${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {\log }_{}}$ 2${\displaystyle {}_{}1\frac{\mathrm{}}{}}$ 1 ${\displaystyle \frac{\frac{16}{}}{}+}$ + ${\displaystyle 1}${ $displaystyle \ left$\ lceil \ $log$ _ ${$2$} {\ frac {1}$ {$6}$ } \$right$ \ $rceil$+ $1$=$$ 4

코드(C)는 1010입니다.

D의 경우

${\displaystyle {F}(D)=p(A)+p(B)+p(C)+{\frac {1}{2}p(D)=parfrac {1}{3}+{\frac {1}{6}+{\frac {1}{2}{cd}{cd} {cd} {cd} {1}$

이진법에서 Z(D) = 0.120

L(D) $={\displaystyle }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle 1\frac{\mathrm{}}{}}$ 1 1${\displaystyle {}_{}}$1 ${\displaystyle \frac{\frac{4}{}}{}}$ ${\displaystyle +}$ +$$ { $displaystyle \ left$\ lceil \ $log$ _ ${$2$}$ {\ $frac {1} {4}$ } \$right$ \ $rceil$+$1$=$$ 3

코드(D)는 111입니다.

알고리즘 분석

프리픽스 코드

Shannon-Fano-Elias 부호화는 바이너리 프리픽스코드를 생성하여 직접 디코딩을 가능하게 합니다.

bcode(x)는 바이너리 코드 앞에 소수점을 추가하여 형성되는 유리수라고 합니다.예를 들어 코드(C)=1010이면 bcode(C)= 0.1010입니다.모든 x에 대해, 그러한 y가 존재하지 않는 경우

${\displaystyle bcode(x)\leq bcode(y)<bcode(x)+2^{-L(x)}}$

모든 코드가 프리픽스 코드를 형성합니다.

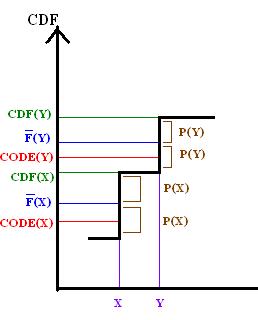
F를 X의 CDF와 비교함으로써 이 성질은 섀넌-파노-엘리아스 부호화에 대해 그래픽으로 입증될 수 있다.

L의 정의에 따르면 다음과 같다.

${\displaystyle 2^{-L(x)}\leq {frac {1}{2}}p(x)}$

그리고 L(y) 뒤의 비트는 F(y)에서 잘려서 코드(y)를 형성하기 때문에 다음과 같이 된다.

${\displaystyle {F}}(y)-bcode(y)\leq 2^{-L(y)}}$

따라서 bcode(y)는 CDF(x) 이상이어야 합니다.

위의 그래프는 e () - d ()> ( )≥ -L ( x ) 、 \ $displaystyle bcode$($y$) - $bcode$( $x$)>$p$ ( x )> p ( x )\ $geq$ 2^ { -$L$ ( x$)}$이므로 프리픽스속성이 됩니다.

코드 길이

평균 코드 길이는 L ${\displaystyle C}$(${\displaystyle }$X ) ${\displaystyle =\underset{x}{}}$ x ${\displaystyle \underset{}{x}}$ X${\displaystyle \underset{}{}}$ (${\displaystyle x}$ )${\displaystyle L}$ (${\displaystyle x}$ ) ${\displaystyle =\underset{x}{}}$ x ${\displaystyle \underset{}{ϵ}}$ ${\displaystyle \underset{}{}}$p (${\displaystyle x}$) （ x ) （${\displaystyle {\log }_{}}$ ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle {}_{}\frac{11}{}}$p (${\displaystyle \frac{x}{}}$ ) ${\displaystyle \rceil }$ +${\displaystyle 1}$ $){$ $display style LC$ ( X ) = \ $sum$ _ {$x$ \ $silon$ X$}$( x \$sum$ ) _ $sum$
따라서 랜덤 변수 X의 엔트로피인 H(X)에 대해서는

${\displaystyle H(X)+1\leq LC(X)<H(X)+2}$

Shannon Fano Elias는 엔트로피보다 X에서 심볼당 1~2비트의 추가 비트를 코드하기 때문에 실제로는 사용되지 않습니다.

레퍼런스