앨리어싱

앨리어싱의 예

이 전체 크기의 이미지는 벽돌 벽의 적절한 샘플링된 이미지가 어떤 모습이어야 하는지를 충분한 해상도의 스크린으로 보여준다.

분해능이 낮아지면 무리에 패턴의 형태로 앨리어싱이 나타난다.

일정한 셔터 속도로 '카메라'가 움직이면 마차 바퀴 효과로 알려진 시간적 별칭이 생성된다.오른쪽으로 움직이는 '카메라'의 속도는 물체가 왼쪽으로 미끄러지면서 끊임없이 같은 속도로 증가한다.24초 고리를 반쯤 지나자 물체가 갑자기 방향을 반대로 바꿔 왼쪽으로 향하는 것처럼 보인다.

신호 처리 및 관련 분야에서 앨리어싱은 샘플링 시 서로 다른 신호를 구별할 수 없게 만드는 효과(또는 서로 별칭)이다.또한 시료에서 재구성된 신호가 원래 연속 신호와 다를 때 나타나는 왜곡이나 아티팩트를 가리킨다.

앨리어싱은 디지털 오디오나 스트로보시 효과와 같이 시간 샘플링된 신호에서 발생할 수 있으며, 시간 앨리어싱이라고 한다.또한 공간적으로 샘플링된 신호(예: 디지털 영상의 뮤레 패턴)에서도 발생할 수 있다. 이러한 유형의 앨리어싱을 공간 앨리어싱이라고 한다.

앨리어싱은 일반적으로 샘플링 전에 입력 신호에 로우패스 필터나 안티앨리어싱 필터(AAF)를 적용하고 신호를 더 높은 샘플링 속도에서 더 낮은 샘플링 속도로 변환할 때 피한다.그런 다음 샘플링된 신호를 연속 도메인으로 복원하거나 신호를 낮은 샘플링 속도에서 높은 샘플링 속도로 변환할 때 적절한 재구성 필터링이 사용되어야 한다.공간적 안티앨리어싱의 경우, 안티앨리어싱의 종류에는 빠른 샘플 안티앨리어싱(FSAA), 멀티샘플 안티앨리어싱, 슈퍼샘플링이 있다.

설명

낮은 해상도로 크기가 조정된 하프톤에 의한 공간 별칭으로 인해 하늘에 있는 점

디지털 이미지를 볼 때 디스플레이나 프린터 장치, 눈과 뇌에 의해 재구성이 이루어진다.샘플링 또는 재구성 중에 영상 데이터가 어떤 식으로든 처리되면 재구성된 영상이 원본 영상과 달라지며 별칭이 나타난다.

공간적 별칭화의 한 예는 벽돌 벽의 화소화되지 않은 이미지에서 관찰된 뮤레 패턴이다.공간적인 안티앨리어싱 기법은 그러한 열악한 픽셀화를 피한다.앨리어싱은 샘플링 단계 또는 재구성 단계에 의해 발생할 수 있으며, 샘플링 앨리어싱 프리앨리어싱과 재구성 앨리어싱 포스트앨리어싱을 호출하여 구별할 수 있다.^[1]

시간 별칭은 비디오 및 오디오 신호 샘플링의 주요 관심사다.예를 들어, 음악은 인간에게 들리지 않는 고주파 성분을 포함할 수 있다.음악이 초당 32,000개의 샘플로 샘플링되는 경우(Hz) 16,000Hz 이상의 주파수 구성 요소(이 샘플링 속도의 나이키스트 주파수)는 음악이 디지털-아날로그 컨버터(DAC)에 의해 재생산될 때 앨리어싱이 발생한다.아날로그 신호의 고주파수는 기록된 디지털 샘플에서 낮은 주파수(잘못된 별칭)로 나타나므로 DAC는 이를 재현할 수 없다.이를 방지하기 위해 시료채취 전 나이키스트 주파수 이상의 구성요소를 제거하기 위해 안티앨리어싱 필터를 사용한다.

비디오 또는 영화 촬영에서 시간 별칭은 제한된 프레임률에서 비롯되며 왜건-휠 효과를 유발하며, 여기서 스포크된 휠은 너무 느리게 또는 심지어 뒤로 회전하는 것처럼 보인다.앨리어싱은 겉보기 회전의 빈도를 바꾸었다.방향의 반전은 음의 주파수로 설명할 수 있다.비디오와 촬영에서 시간 별칭 주파수는 카메라의 프레임률에 의해 결정되지만, 별칭 주파수의 상대적 강도는 촬영 중 셔터 타이밍(노출 시간)이나 시간 별칭 감소 필터의 사용에 의해 결정된다.^[2]^{[unreliable source?]}

비디오 카메라와 같이 대부분의 샘플링 방식은 주기적이다. 즉, 시간이나 공간에서의 샘플링 빈도가 특징적이다.디지털 카메라는 카메라의 초점면에서 도당 또는 라디안당 일정한 수의 샘플(픽셀) 또는 mm당 샘플을 제공한다.오디오 신호는 아날로그-디지털 변환기로 샘플링(디지털화)되며, 초당 일정한 샘플 수가 생성된다.앨리어싱의 가장 극적이고 미묘한 예 중 일부는 샘플링되는 신호가 주기적인 함량을 가질 때 발생한다.

대역제한함수

실제 신호는 지속시간이 유한하며, 푸리에 변환에 의해 정의된 주파수 함량은 상한이 없다.그러한 기능이 샘플링될 때 항상 어느 정도의 앨리어싱이 발생한다.주파수 내용이 경계(대역제한)된 함수는 시간영역에서 지속시간이 무한하다.대역폭에 의해 결정되는, 충분히 높은 속도로 샘플링한다면, 이론적으로, 원래의 기능은, 무한한 샘플 집합으로부터 완벽하게 재구성될 수 있다.

밴드패스 신호

때때로 앨리어싱은 대역 통과 신호라고 불리는 저주파 함량이 없는 신호에 의도적으로 사용된다.저주파 별칭을 생성하는 과소 샘플링은 낮은 속도로 샘플링하기 전에 신호를 낮은 주파수로 변환하기 때문에 적은 노력으로 동일한 결과를 생성할 수 있다.일부 디지털 채널라이저는 계산 효율을 위해 이러한 방식으로 앨리어싱을 이용한다.^[3](샘플링(신호 처리), 나이키스트 레이트(샘플링과 상대적) 및 필터 뱅크를 참조하십시오.)

사인파 함수 샘플링

그림.2 왼쪽 상단: 애니메이션은 일정한 주파수/속도,

f_{s}.

.

f_{s

에서 샘플링되는 동안 주파수가 증가하는 사인파 스냅샷을 그린다.

}

오른쪽 상단

f_{s}.

:실제 연속형 푸리에 변환의 해당 스냅샷.실제 주파수를 나타내는 0이 아닌 단일 성분은 모호함이 없음을 의미한다.오른쪽 아래:사용 가능한 샘플의 이산 푸리에 변환.두 개의 성분이 있다는 것은 표본이 적어도 두 개의 서로 다른 사인파(syncoid)를 맞출 수 있다는 것을 의미하며, 그 중 하나는 실제 주파수와 일치한다.왼쪽 아래:부수적인 정보가 없는 경우, 기본 재구성 알고리즘은 저주파수 사인파이를 생성한다.

사인파(synusoid)는 주기 함수의 중요한 유형으로, 현실적인 신호는 종종 서로 다른 주파수와 다른 진폭(예를 들어 푸리에 시리즈 또는 변환)의 많은 사인파(synusoid)의 합으로 모델링되기 때문이다.앨리어싱이 개별 사인파에게 어떤 영향을 미치는지 이해하는 것은 사인파에게 무슨 일이 일어나는지 이해하는 데 유용하다.

$주파수 s$ f( $간격$ 1/ $f s)$ 에서 함수를 샘플링할 때, 다음 시간 $(t)$ 함수에서 동일한 샘플 세트를 산출한다: { $sin(2π(f+Nf s)$ t + $φ),$ $N$ = 0 $, \pm$ 1 $,$ $\pm$ 2 $,$ $\pm3,...$ }. 표본의 주파수 스펙트럼은 모든 주파수에서 동일하게 강한 반응을 일으킨다.부수적인 정보가 없으면 원래 기능의 빈도가 모호하다.그래서 기능과 그 주파수는 서로 별칭이라고 한다.삼각측량 아이덴티티 참고:

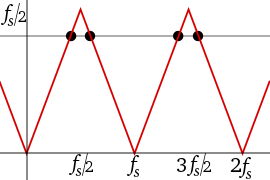
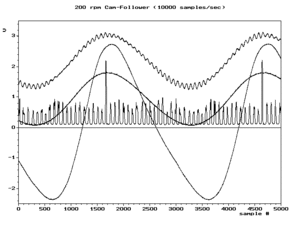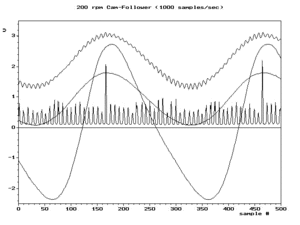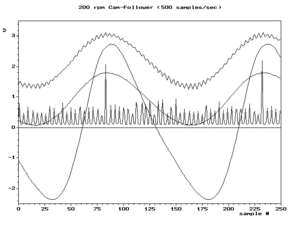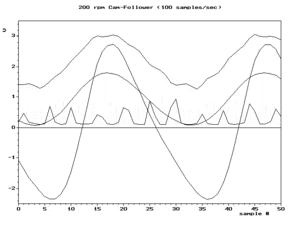
\sin(2\pi (f+Nf_{\rm {s}})t+\phi )=\left\{{\begin{array}{ll}+\sin(2\pi (f+Nf_{\rm {s}})t+\phi ),&f+Nf_{\rm {s}}\geq 0\\-\sin(2\pi  f+Nf_{\rm {s}} t-\phi ),&f+Nf_{\rm {s}}<0\\\end{array}}\right.

우리는 모든 별칭 주파수를 양의 $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ 으로 쓸 수 있다: $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ N $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ ( $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ ) $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ f + N $f_{_{N}}(f)\triangleq \left|f+Nf_{\rm {s}}\right|$ s $displaystyle f_{N}(f)\triangleq \left+Nf_{\rm {s}\right$ 예를 들어 그림.2의 오른쪽 하단 프레임의 스냅샷은 실제 주파수 $f$ ${\displaysty$ f $}$ 와 $f_{_{-1}}(f)$ 구성요소를 나타낸다. $f_{_{-1}}(f)$ $){\displaystyle f_{-1}(f$ 애니메이션 도중 $f$ $f_{_{-1}}(f)$ $f$ 이(가) 증가함에 $f$ 따라 f $f_{_{-1}}(f)$ - $){\displaystyle f_{-1}(f)}$ 은 $f_{_{-1}}(f)$ (가) 감소한다.그것들이 같은 지점 $($ = $(f=f_{s}/2)$ $(f=f_{s}/2)$ / 2 $(f=f_{s}/2)$ ) ${\displaystyle (f=f_{s}/2$ )은 $(f=f_{s}/2)$ 나이키스트 주파수로도 알려져 있는 접이 주파수라고 불리는 대칭의 축이다.

앨리어싱은 샘플에서 원래 파형을 재구성하려고 할 때 중요하다.가장 일반적인 재구성 기법은 $f_{_{N}}(f)$ N $f_{_{N}}(f)$ ( $f_{_{N}}(f)$ ) $f_{_{N}(f)$ 개의 주파수 $f_{_{N}}(f)$ 중에서 가장 작은 주파수를 생성한다.따라서 $f_{0}(f)$ 으로 f $f_{0}(f)$ ( $f_{0}(f)$ ) $f_{0}(f)$ 이(가) 고유한 최소값이 되는 $f_{0}(f)$ 것이 중요하다.그것을 위해 필요하고 충분한 조건은 nyquist 조건이라 불리는 $f_{s}/2>|f|,$ $f_{s}/2>|f|,$ / $f_{s}/2>|f|,$ > $f_{s}/2>|f|,$ , ${\displaystyle f_{s}/2>$ f $,}$ 이다.그림.2의 왼쪽 하단 프레임은 사용 가능한 샘플의 전형적인 재구성 결과를 나타낸다. $f$ $f$ 이(가) 나이키스트 주파수를 초과할 $f$ 때까지 재구성은 실제 파형(왼쪽 위 프레임)과 일치한다.이후 상부 프레임의 저주파 별칭이다.

접기

아래 그림은 샘플링으로 인한 앨리어싱에 대한 추가적인 묘사를 제공한다.0.6 $f$ 의_s 주파수에서 단일 사인파 및 0 $.4$ $f s s$ $,$ 1 $.4 f,$ 1.6 $f$ 의_s 일부 별칭에 대한 진폭 대 주파수(시간이 아님)를 나타내는 그래프는 그림.3의 4개의 검은 점처럼 보일 것이다.빨간색 선은 단색 부분(f $s /2$ 와_s f 사이)을 따라 사인파의 주파수와 진폭을 조정한다면 4개의 점의 경로(로시)를 나타낸다.진폭 대 주파수를 변경하기 위해 어떤 기능을 선택하든, 그래프는 0과 $s$ f 사이의 대칭을 나타낼 것이다 $.$ 폴딩은 종종 그림.4와 같이 실제 가치 표본의 주파수 스펙트럼을 볼 때 실제로 관찰된다.

그림 3: 검은 점들은 서로의 별칭이다.적색 실선은 주파수에 따라 변하는 진폭의 예다.빨간색 점선은 별칭의 해당 경로다.

그림.4: 44,100개의 샘플/sec로 샘플링된 음악의 푸리에 변환은 나이키스트 주파수(22,050Hz)를 중심으로 대칭("폴딩"이라고 함)을 나타낸다.

그림.5: 접이식 주파수와 주기성을 보여주는 주파수 앨리어싱 그래프.

f s /2

이상의 주파수에는

f s /2

이하의 별칭이 있으며

,

이 값은 이 그래프에 의해 주어진다.

그리드 라인에 의해 표시된 속도(

f s

)로 샘플링했을 때 동일한 실제 및 가상 샘플 포인트 세트에 맞는 색상의 금 및 청록색인 두 개의 복합 사인파.

여기

에_gold 표시된 예는 다음과 같다:

f cyan -1

= f

(f gold)

=

f s

– f

복합 사인파

콤플렉스 사인파(complex synusid)는 샘플이 복잡한 숫자인 파형을 말하며, 이를 구별하기 위해서는 음수 주파수의 개념이 필요하다. $이$ 경우, 별칭의 빈도는 단지: $f N ($ f $)$ = f + N $f$ 로_s 주어진다 $.$ 따라서 f가 0에서 f로 $s$ 증가함에 따라 $f -1 (f$ $)$ 도 증가한다(- $f$ 에서_s 0으로 증가함 $).$ 결과적으로, 복잡한 사인파이는 접히는 모습을 보이지 않는다.

샘플 주파수

6가지 다른 속도로 채취한 샘플에서 재구성된 파형 4개 그림.파형 중 2개는 6개 속도 모두에서 앨리어싱을 피할 수 있도록 충분히 샘플링된다.다른 두 가지는 낮은 비율로 증가하는 왜곡(별칭)을 보여준다.

원래 신호의 가장 높은 주파수 성분에 대해 $s f/2$ > f 조건이 충족되면, 나이키스트 기준이라는 조건인 모든 주파수 성분에 대해 충족된다.그것은 일반적으로 샘플링되기 전에 고주파 성분을 감쇠시키기 위해 원래 신호를 필터링하여 근사치를 구한다.이러한 감쇠된 고주파 구성 요소는 여전히 저주파 별칭을 생성하지만 일반적으로 문제를 일으키지 않을 정도로 낮은 진폭에서 생성된다.특정 샘플 주파수를 예상하고 선택한 필터를 안티앨리어싱 필터라고 한다.

필터링된 신호는 큰 추가 왜곡 없이 보간 알고리즘에 의해 재구성될 수 있다.대부분의 샘플링된 신호는 단순히 저장되고 재구성되지 않는다.그러나 (Whittaker-Shannon 보간 공식을 통한) 이론적 재구성의 충실성은 샘플링의 효과에 대한 관습적인 척도다.

역사적 용법

역사적으로 앨리어싱이라는 용어는 초헤테로디네 수신기의 작용 때문에 라디오 공학에서 진화했다.수신기가 원하는 신호와 동일하게 국부 오실레이터(LO) 주파수에서 멀리 떨어진 RF 주파수에서 원하지 않는 신호인 헤테로디션을 통해 RF에서 IF로 여러 신호를 낮은 주파수로 이동시킬 때, 그러나 LO의 잘못된 측면에서는 원하는 것과 동일한 IF 주파수로 끝날 수 있다.충분히 강하면 원하는 신호의 수신을 방해할 수 있다.이 원하지 않는 신호는 원하는 신호의 영상 또는 별칭으로 알려져 있다.

각도 앨리어싱

앨리어싱은 연속 신호를 캡처하거나 생성하기 위해 이산 원소를 사용할 때마다 발생하며 주파수 모호성을 유발한다.

공간적 앨리어싱(각진 주파수의 특유한)은 3D 표시장치나 음의 파장 합성에 있어서와 같이 광장 또는 음장을 이산 원소로 재현할 때 발생할 수 있다.^[4]

이러한 앨리어싱은 렌즈 인쇄 포스터와 같은 이미지에서 볼 수 있다: 각도가 낮은 경우, 각도가 낮은 경우, 예를 들어 좌우로 움직이면, 2D 영상이 처음에 변하지 않는다(그래서 왼쪽으로 움직이는 것처럼 보인다), 다음 각도로 이동할 때 영상이 갑자기 바뀐다(그래서 오른쪽으로 점프한다).d 진폭은 4D 광장의 각도 별칭인 영상의 각도 분해능(및 주파수의 경우 뷰어의 가로 방향 이동 속도)에 해당한다.

2D 영상과 입체 안경에 의해 생성된 3D 필름에서 시청자의 움직임에 시차(paralax)가 없다는 것은(3D 필름에서 영상이 축에서 회전하는 것처럼 보이므로 그 효과를 "요잉"이라고 한다)의 각도 분해능 상실로, 모든 각도 주파수가 0(상수)으로 가칭되는 것으로 유사하게 볼 수 있다.

더 많은 예

오디오 예

Sawtoss 앨리어싱 데모(0:06)

440Hz 대역 제한, 440Hz 앨리어싱, 880Hz 대역 제한, 880Hz 앨리어싱, 1,760Hz 대역 제한, 1,760Hz 앨리어싱

이 파일을 재생하는 데 문제가 있으십니까?미디어 도움말을 참조하십시오.

앨리어싱의 질적 효과는 다음의 오디오 시연에서 들을 수 있다.6개의 톱니파가 연속적으로 연주되는데, 처음 두 톱니바퀴는 기본 주파수가 440Hz(A4)이고, 두 번째 톱니바퀴는 기본 주파수가 880Hz(A5)이며, 마지막 두 톱니바퀴는 1,760Hz(A6)이다.톱니바퀴는 밴드제한(별칭이 아닌) 톱니바퀴와 앨리어스 톱니바퀴 사이를 번갈아 가며 샘플링 속도는 22,05kHz이다.밴드제한 톱니토스는 톱니토스 파형의 푸리에 시리즈에서 합성되어 나이키스트 주파수 이상의 고조파가 존재하지 않는다.

낮은 주파수의 앨리어싱 왜곡은 기본 주파수가 높을수록 점점 뚜렷해지고, 밴드제한 톱니바퀴는 1,760Hz로 여전히 선명하지만, 기본보다 낮은 주파수에서 윙윙거리는 소리와 함께 성능이 저하되고 가혹하다.

방향 찾기

지진파에 의한 지구물리학적 탐사에서와 같이, 파동 신호의 도착 방향을 추정하는 데 사용되는 안테나 배열이나 마이크 배열에서도 공간 별칭의 형태가 발생할 수 있다.파장은 파장당 2점 이상 촘촘하게 샘플링해야 하며, 그렇지 않으면 파장 도착 방향이 모호해진다.^[5]

참고 항목

메모들

참조

^ Mitchell, Don P.; Netravali, Arun N. (August 1988). Reconstruction filters in computer-graphics (PDF). ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques. Vol. 22. pp. 221–228. doi:10.1145/54852.378514. ISBN 0-89791-275-6.
^ 테시브, LLC(2010)."시간 필터 기술 설명"
^ harris, frederic j. (August 2006). Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-146511-4.
^ 스탠퍼드 라이트 필드 아카이브
^ Flanagan, James L, AT&T Tech. J, 1985, 64, 페이지 983–995, "지연 조향 마이크 어레이의 빔 폭과 사용 가능한 대역폭"

추가 읽기

파르, 맷; 험프리스, 그렉(2010년 6월 28일)물리적 기반 렌더링: 이론에서 실행까지.모건 카우프만ISBN 978-0-12-375079-2.7장 (샘플링 및 재구성)2013년 3월 3일 검색됨

외부 링크

Tektronix 애플리케이션 엔지니어가 YouTube에서 샘플링 오실로스코프에 의한 앨리어싱
La Vida Leica의 Anti-Aliasing Filter Primer, 녹화된 이미지에 대한 목적과 효과 설명
앨리어싱 효과를 보여주는 대화형 예

[mitchell-1] Mitchell, Don P.; Netravali, Arun N. (August 1988). Reconstruction filters in computer-graphics (PDF). ACM SIGGRAPH International Conference on Computer Graphics and Interactive Techniques. Vol. 22. pp. 221–228. doi:10.1145/54852.378514. ISBN 0-89791-275-6.

[tessive-2] 테시브, LLC(2010)."시간 필터 기술 설명"

[harris-3] rris, frederic j. (August 2006). Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-146511-4.

[lightfield-4] 스탠퍼드 라이트 필드 아카이브

[flangan-5] Flanagan, James L, AT&T Tech. J, 1985, 64, 페이지 983–995, "지연 조향 마이크 어레이의 빔 폭과 사용 가능한 대역폭"

[1]

[2]

[3]

[4]

[5]

v t 디지털 신호 처리
이론	검출이론 이산 신호 추정 이론 니키스트-샤논 샘플링 정리
하위 필드	오디오 신호 처리 디지털 이미지 처리 음성 처리 통계 신호 처리
기술	Z-변환기 고급 z 변환기 일치 Z 변환 방법 이린형 변환 상수 Q 변환 이산 코사인 변환(DCT) 이산 푸리에 변환(DFT) 이산 시간 푸리에 변환(DTFT) 임펄스 불발성 적분 변환 라플라스 변환 포스트의 반전 공식 별자형 변환 잭 변환
샘플링	앨리어싱 안티앨리어싱 필터 다운샘플링 나이키스트 속도/주파수 오버샘플링 수량화 샘플링 속도 과소표본 업샘플링

Search