일치 Z 변환 방법

Matched Z-transform method
5번째 순서 체비셰프 타입 II 로우패스 필터의 s-평면 폴과 0은 이산 시간 필터로 근사치되어야 한다.
T = 1/10초와 일치하는 Z 변환 방법을 사용하여 z 평면에 매핑된 이산 시간 체비셰프 필터의 z 평면 폴과 0. 라벨이 표시된 주파수 포인트와 밴드 에지 점선은 s 평면 지도에서 iΩ 축을 따라가는 주파수를 z-평면의 단위 원 위에 어떻게 배치하는지를 보여주기 위해 z=eiωT 함수를 통해 매핑되었다.

일치 Z-변환법(matched Z-transform method, pole-zero[1][2] matching method)이라고도 하며,[3] 약칭 MPZ 또는 MZT라고 하는 것은 연속 시간 필터 설계를 이산 시간 필터(digital-time filter) 설계로 변환하는 기법이다.[4]

방법은 s-평면 설계의 모든 극과 0을 z-평면 z= 에 매핑하는 방식으로 작동한다. 샘플링 간격 = / [5] 따라서 전송 함수가 있는 아날로그 필터:

디지털 전송 기능으로 변환됨

gain 은(는) 원하는 게인을 정규화하도록 조정해야 하며, 으로s = =0 z = 1{\}을를) 설정하고 k d [3][6]에 대한 해결을 수행하면 아날로그 필터의 이득과(으(으)에 대해 일반적으로 DC에서 아날로그 필터가 일치하도록

매핑은 z-평면의 축을 z-평면의 단위 원을 반복적으로 감싸므로 Nyquist 주파수보다 큰 0(또는 극)은 앨리어싱된 위치에 매핑된다.[7]

아날로그 전송 기능이 0보다 많은 극을 갖는 (공통)의 경우, = 의 은z= - {\z=-에 배치하여 Nyquist 주파수로 전환될 수 있으며 이는 전송 함수를→ - 1으로 떨어뜨리게 한다.그는 이선형 변환(BLT)과 같은 태도다.[1][3][6][7]

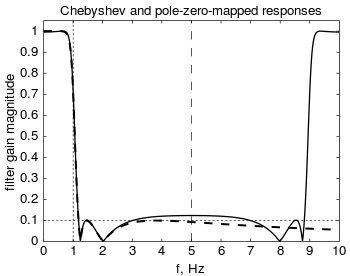
이 변환은 안정성과 최소 위상을 보존하지만 시간 영역 및 주파수 영역 응답을 보존하지 않으므로 널리 사용되지 않는다.[8][7] 보다 일반적인 방법으로는 BLT와 임펄스 침입 방법이 있다.[4] MZT는 BLT보다 고주파 응답 오류를 적게 제공하지만, 0을 더 추가하면 교정이 쉬워지는데, 이를 MZTi('개선'의 경우)라고 한다.[9]

디지털 제어 분야에서 일치하는 Z-변환법의 특정한 적용은 Ackermann의 공식에 있다. 이 공식은 제어 가능한 시스템의 극을 변화시킨다. 일반적으로 불안정한(또는 가까운) 위치에서 안정적인 위치로 변화시킨다.

공칭 컷오프 주파수 1Hz, 샘플링 속도 1/T = 10Hz에 대한 필터의 응답(분해) 및 이산 시간 근사치(고형) 이산 시간 필터는 응답의 주기적 복사본으로부터의 간섭으로 인해 정지 대역에서 체비셰프 에퀴리플 속성을 재현하지 않는다.

참조

  1. ^ a b Won Young Yang (2009). Signals and Systems with MATLAB. Springer. p. 292. ISBN 978-3-540-92953-6.
  2. ^ Bong Wie (1998). Space vehicle dynamics and control. AIAA. p. 151. ISBN 978-1-56347-261-9.
  3. ^ a b c Arthur G. O. Mutambara (1999). Design and analysis of control systems. CRC Press. p. 652. ISBN 978-0-8493-1898-6.
  4. ^ a b Al-Alaoui, M. A. (February 2007). "Novel Approach to Analog-to-Digital Transforms". IEEE Transactions on Circuits and Systems I: Regular Papers. 54 (2): 338–350. doi:10.1109/tcsi.2006.885982. ISSN 1549-8328. S2CID 9049852.
  5. ^ S. V. Narasimhan and S. Veena (2005). Signal processing: principles and implementation. Alpha Science Int'l Ltd. p. 260. ISBN 978-1-84265-199-5.
  6. ^ a b Franklin, Gene F. (2015). Feedback control of dynamic systems. Powell, J. David, Emami-Naeini, Abbas (Seventh ed.). Boston: Pearson. pp. 607–611. ISBN 978-0133496598. OCLC 869825370. Because physical systems often have more poles than zeros, it is useful to arbitrarily add zeros at z = -1.
  7. ^ a b c Rabiner, Lawrence R; Gold, Bernard (1975). Theory and application of digital signal processing. Englewood Cliffs, New Jersey: Prentice-Hall. pp. 224–226. ISBN 0139141014. The expediency of artificially adding zeros at z = —1 to the digital system has been suggested ... but this ad hoc technique is at best only a stopgap measure. ... In general, use of impulse invariant or bilinear transformation is to be preferred over the matched z transformation.
  8. ^ Jackson, Leland B. (1996). Digital Filters and Signal Processing. Springer Science & Business Media. p. 262. ISBN 9780792395591. although perfectly usable filters can be designed in this way, no special time- or frequency-domain properties are preserved by this transformation, and it is not widely used.
  9. ^ Ojas, Chauhan; David, Gunness (2007-09-01). "Optimizing the Magnitude Response of Matched Z-Transform Filters ("MZTi") for Loudspeaker Equalization". Audio Engineering Society. Archived from the original on July 27, 2019. Alt URL