회전 대칭

맨 섬 깃발에 나타나는 트리스켈리온은 중심을 중심으로 1/3 회전할 때 동일하게 나타나기 때문에 회전 대칭을 가집니다.외관이 세 가지 방향에서 동일하기 때문에 회전 대칭이 세 배입니다.

기하학에서 반지름 대칭이라고도 하는 회전 대칭은 일부 회전 후에 모양이 같아 보일 때 갖는 특성입니다.물체의 회전 대칭도는 각 회전마다 정확히 동일하게 보이는 뚜렷한 방향의 수입니다.

90° 회전하는 정사각형과 같은 특정 각도에서 회전할 때 일부 대칭이 되는 기하학적 개체는 구, 원 및 기타 ^[1]^[2]구상체뿐입니다.

형식적 대우

형식적으로 회전 대칭은 m차원 유클리드 공간에서의 일부 또는 모든 회전과 관련된 대칭이다.회전은 직접 등각선, 즉 방향을 유지하는 등각선입니다.따라서 회전 대칭의 대칭 그룹은 E(m)의⁺ 부분군입니다(유클리드 그룹 참조).

모든 점의 모든 회전에 대한 대칭은 모든 변환에 대한 변환 대칭을 의미하므로 공간은 균질하고 대칭 그룹은 전체 E(m)입니다.벡터장에 대한 대칭의 수정된 개념으로 대칭 그룹은 E(m)가⁺ 될 수도 있습니다.

점을 중심으로 한 회전에 대한 대칭성을 위해 우리는 그 점을 원점으로 삼을 수 있다.이러한 회전은 행렬식 1을 갖는 m×m 직교 행렬의 그룹인 특수 직교 그룹 SO(m)를 형성한다.m = $3$ 의 $경우$ , 이것은 회전 그룹 SO(3)이다.

단어의 또 다른 정의에서, 물체의 회전군은 E(n) 내의⁺ 대칭군, 즉 직접 등각체의 그룹, 즉 완전한 대칭군과 직접 등각체의 그룹의 교차점입니다.키랄 객체의 경우 전체 대칭 그룹과 동일합니다.

물리법칙은 공간의 다른 방향을 구별하지 않으면 SO(3)-불변합니다.노에터의 정리 때문에 물리적 시스템의 회전 대칭은 각운동량 보존 법칙과 동일합니다.

이산 회전 대칭

특정 점(2D) 또는 축(3D)에 대한 n차 회전 대칭 또는 n차 이산 회전 대칭이라고도 하는 n차 회전 대칭은 360°/n(180°, 120°, 90°, 72°, 60°, 51)의 각도로 회전하는 것을 의미합니다.3⁄7° 등)는 오브젝트를 변경하지 않습니다."1중" 대칭은 대칭이 아닙니다(360° 회전 후 모든 물체는 비슷해 보입니다).

n배 대칭의 표기법은 C 또는 단순히 "n"입니다_n.실제 대칭 그룹은 n과 함께 대칭점 또는 축으로 지정됩니다.각 대칭점 또는 축에 대해 추상군 유형은 순서 n, Z의_n 순환군입니다.후자의 경우 C 표기법을_n 사용하지만 기하학적 C와 추상적_n C를 구별해야 한다. 기하학적으로 다른 동일한 추상적 그룹 유형의 대칭 그룹이 있다. 3D 순환 대칭 그룹을 참조한다.

기본 영역은 360°/n 섹터입니다.

추가 반사 대칭이 없는 예:

n = 2, 180°:다이야드, 문자 Z, N, S, 음양기호의 윤곽은 색상은 아니지만 유니온기(깃발의 대각선을 따라 나뉘고 깃발의 중심점을 중심으로 회전하는 것)
n = 3, 120°:트라이어드, 트리스켈리온, 보롬환. 때로는 3변 대칭이라는 용어를 사용한다.
n = 4, 90°: 테트라드, 스와스티카
n = 6, 60°:헥사드, 다윗의 별(이것에는 추가적인 반사 대칭이 있음)
n = 8, 45°:옥타드, 옥타곤 무카르나, 컴퓨터 생성(CG), 천장

C는_n 2차원에서는 정n면 다각형, 3차원에서는 정n면 피라미드의 회전군이다.

예를 들어 100°의 각도와 관련하여 회전 대칭이 존재하는 경우, 20° 중 하나에 대해서도 100°와 360°의 최대 공약수이다.

회전 대칭(수직 축도 있음)을 가지지만 거울 대칭이 없는 일반적인 3D 물체는 프로펠러입니다.

예

C2(더 보기)	C3(더 보기)	C4(더 보기)	C5(더 보기)	C6(더 보기)
이중 진자 프랙탈	원형 교차로 교통 표지판		미국 200주년 별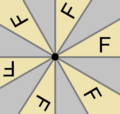
장기의 시작 위치	스놀델레프 스톤의 연동형 술뿔 디자인

동일한 점을 통과하는 다중 대칭 축

여러 대칭 축이 같은 점을 통과하는 이산 대칭의 경우 다음과 같은 가능성이 있습니다.

n배축 외에 n개의 수직 2배축: 2n( $nn2)$ 차수의 2면체군_n D.이것은 일반 프리즘의 회전군, 즉 일반 이원체입니다.같은 표기법이 사용되더라도 기하학적 D와_n 추상적 D는 구별되어야 한다. 기하학적으로 다른 추상적 그룹 유형의 대칭 그룹이 있다. 3D의 이면체 대칭 그룹을 참조하라.
4×3배 및 3×2배 축: 정4면체의 12차 회전군 T.그룹은 교대 그룹₄ A와 동형입니다.
3×4배, 4×3배, 6×2배 축: 정육면체와 정팔면체의 24차 회전군 O.그룹은 대칭 그룹₄ S와 동형이다.
6×5배, 10×3배, 15×2배 축: 12면체와 20면체의 60차 회전군 I.그룹은 교대 그룹₅ A와 동형입니다.이 그룹에는 D의 10가지₃ 버전과 D의₅ 6가지 버전이 포함됩니다(프리즘 및 반프리즘과 같은 회전 대칭).

Platonic 솔리드의 경우, 2중 축은 반대편 가장자리의 중간점을 통과하며, 그 수는 가장자리 수의 절반입니다.다른 축은 반대 정점과 반대 면의 중심을 통과합니다. 단, 3중 축은 각각 하나의 정점과 한 면의 중심을 통과합니다.

모든 각도에 대한 회전 대칭

모든 각도에 대한 회전 대칭은 2차원에서 원형 대칭이다.기본 도메인은 하프라인입니다.

3차원에서는 원통형 대칭과 구형 대칭을 구별할 수 있습니다(한 축을 중심으로 회전할 때 또는 어떤 회전에도 변화가 없음).즉, 원통 좌표를 사용하는 각도에 의존하지 않고 구면 좌표를 사용하는 각도에 의존하지 않습니다.기본 도메인은 축을 통과하는 반평면과 반경 반직선입니다.축대칭 또는 축대칭은 도넛(토러스)처럼 원통형 대칭 또는 축대칭(즉 중심축에 대한 회전 대칭)을 가진 물체를 가리키는 형용사이다.대략적인 구면 대칭의 예는 지구이다(밀도와 다른 물리적, 화학적 특성과 관련하여).

4D에서 평면에 대한 연속 또는 이산 회전 대칭은 교차점에 대한 모든 수직 평면에서의 해당 2D 회전 대칭에 해당합니다.물체는 예를 들어 듀오실린더 및 다양한 규칙 이중 프리즘의 경우와 같이 예를 들어 두 개의 회전 대칭 2D 도형의 데카르트 곱인 경우 두 개의 수직 평면에 대한 회전 대칭을 가질 수도 있다.

회전대칭과 병진대칭

2배와 4배 로토센타의 원시 세포 내 배치.기본 도메인은 노란색으로 표시됩니다.	2배, 3배, 6배 로토센타의 원시 셀 내 배열(2배 및 3배 기호의 조합으로 6배 기호가 고려됨)로, 2배 대칭의 경우에만 평행사변형의 모양이 다를 수 있습니다.이 경우 p6은 노란색으로 기본 도메인을 나타낸다.

2중 회전 대칭과 단일 변환 대칭은 Frieze 그룹 중 하나입니다.원시 세포마다 두 개의 로또센터가^{[definition needed]} 있다.

이중 변환 대칭과 함께 회전 그룹은 원시 셀당 축이 있는 다음과 같은 벽지 그룹입니다.

p2(2222) : 4×2배, 평행, 직사각형 및 마름모꼴 격자의 회전군.
p3(333) : 3×3배, 어떤 격자의 회전군도 아니다(모든 격자는 거꾸로 되어 있지만 이 대칭에는 적용되지 않는다).예를 들어 정삼각형 타일링의 회전군이 교대로 착색된 정삼각형 타일링의 회전군이다.
p4(442) : 2×4배, 2×2배, 정사각형 격자의 회전군.
p6(632) : 1×6배, 2×3배, 3×2배, 육각형 격자의 회전군.
2배 로토센트(가능한 4배 및 6배 포함)가 존재한다면 1/2 인수로 스케일링된 변환 격자와 동일한 격자의 변환을 형성한다.한 차원에서의 변환 대칭의 경우, "격자"라는 용어는 적용되지 않지만 유사한 특성이 적용된다.
3중 회전 중심(가능한 6중 회전 포함)은 변환 격자와 동일한 정육각형 격자를 형성하고, 30°(또는 동등한 90 $°)$ ${\frac {1}{3}}{\sqrt {3}}$ 하며, ${\frac {1}{3}}{\sqrt {3}}$ 1 3 $($ 3}}{\ $displaystyle {3}})$ 로 스케일링합니다.
4중 로토센트가 존재하는 경우, 45 $°$ 회전하여 ${\frac {1}{2}}{\sqrt {2}}$ ${\frac {1}{2}}{\sqrt {2}}$ 된 정사각형 격자와 동일한 정사각형 격자를 형성합니다(\ $displaystyle {1}{2}}{\displayrt {2}}).$
6중 로또센트가 존재한다면, 변환 격자를 번역한 정육각형 격자를 형성한다.

격자의 축척은 단위 면적당 점 수를 축척 요인의 제곱으로 나눕니다.따라서 원시세포 1개당 2배, 3배, 4배, 6배 로또센타의 수는 각각 4, 3, 2, 1이며, 2배 등의 특수한 경우로서 4배도 포함한다.

한 지점에서 3배 회전 대칭과 다른 지점에서 2배 회전 대칭(또는 평행 축에 대한 3D에서는 2배 회전 대칭)은 회전 그룹 p6, 즉 어떤 지점(또는 3D에서는 6배 회전 대칭)을 의미한다.이러한 한 쌍의 로또센타에 의해 생성되는 대칭의 변환 거리는 $2{\sqrt {3}}$ 의 $2{\sqrt {3}}$ 인 $2{\sqrt {3}}$ 2 $(\$ 2 ${\sqrt {3}})$ 입니다.

유클리드 평면	쌍곡면
p6, [6,3],⁺ (632)(색상 있음) 및 p6m, [6,3], (*632)(색상 없음)의 예인 헥사키스 삼각형 타일링. 색상이 무시되지 않으면 선이 반사축, 색상이 무시되지 않으면 특수 종류의 대칭축: 반사가 색을 되돌린다.세 방향의 직사각형 선 그리드를 구분할 수 있습니다.	[7,3](⁺732) 대칭과 [7,3], (*732) (색상 없음)의 예인 3-7 키롬빌 주문

「」를 참조해 주세요.

레퍼런스

Weyl, Hermann (1982) [1952]. Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.

외부 링크

Wikimedia Commons의 회전 대칭에 관한 미디어
수학의 회전 대칭 예 재미있음

[1] 균질한 3개의 마니폴드에서 와인가텐 구의 회전 대칭.Jos ́e A에 의해.알베즈, 파블로 미라

[2] 유전체 구 배열의 연속체에서의 위상 구속 상태.러시아 크라스노야르스크 LV 키렌스키 물리학 연구소, Dmitrii N. Maksimov 작성

[1]

[2]

Search

회전 대칭

네임스페이스

더

목차