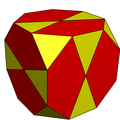
이코시다데카헤드론

Icosidodecahedron
이코시다데카헤드론
Icosidodecahedron.jpg
(모델을 회전하려면 여기를 클릭하십시오.)
유형 아르키메데스 고체
균일다면체
요소들 F = 32, E = 60, V = 30(수평 = 2)
옆얼굴 20{3}+12{5}
콘웨이 표기법 AD
슐레플리 기호 r{5,3}
t1{5,3}
와이토프 기호 2 3 5
콕시터 다이어그램 CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png
대칭군 Ih, H3, [5,3], (*532), 주문 120
회전군 I, [5,3],+ (532), 주문 60
디헤드각 142.62°
참조 U24, C28, W12
특성. 반경형 볼록 퀘이레겔러
Polyhedron 12-20 max.png
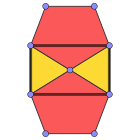채색면 		Polyhedron 12-20 vertfig.svg
3.5.3.5
(Vertex 그림)
Polyhedron 12-20 dual max.png
롬빅 삼권면체
(이중 다면체) 		Polyhedron 12-20 net.svg
그물
이코시다데코헤드론의 3D 모델

기하학에서 이코시다데카헤드론은 20개의 삼각형 면과 12개의 오각형 면을 가진 다면체다. 이코시다데카헤드론은 30개의 정점이 동일하며, 각각 두 개의 삼각형과 두 개의 펜타곤이 만나고, 60개의 동일한 가장자리가 각각 오각형에서 삼각형을 분리한다. 이와 같이 그것은 아르키메데스 고형물 중 하나이며, 더욱 특히 quasiregular 다면체 중 하나이다.

기하학

이코시다데카헤드론은 이코사헤드론 대칭을 가지며, 이코사헤드론은 도데카헤드론과 그것의 이중 이코사헤드론의 합성어로, 이코사이드론의 정점이 둘 중 어느 한쪽 가장자리의 중간점에 위치한다.

그것의 이중 다면체는 Rhombic 삼면체다면체다면체 이코시다데코헤드론은 6개의 평면을 따라 분할되어 한 쌍의 오각형 로툰대를 형성할 수 있는데, 존슨 고형분자들 사이에 속한다.

이코시다데코헤드론은 두 개의 로툰대(오각형 오각형 오각형 오각형 오각형 오각형 오각형 오각형 오각형 로툰다, 존슨 고형물 중 하나)의 조합으로 오각형 자이로비로툰다라고 볼 수 있다. 이 형태에서 대칭은 D5d, [10,2+], (2*5) 순서 20이다.

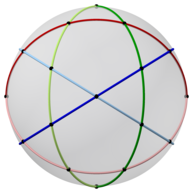
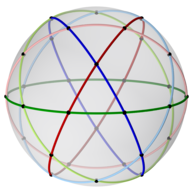
이코시다데카헤드론의 와이어프레임 모양은 6개의 평평한 정규 디카곤으로 구성되며, 30개의 꼭지점 각각에서 쌍으로 만난다.

이코시다데카헤드론은 6개의 중앙 디카곤을 가지고 있다. 구체로 투영된 그들은 6개의 거대한 원을 정의한다. 벅민스터 풀러는 이 6개의 원과 15개의 다른 원과 10개의 다른 원과 함께 구면 이코사면체의 31개의 원들을 정의하기 위해 사용했다.

데카르트 좌표, 평행 좌표.

단위 가장자리가 있는 ICosidodechedron의 정점에 대한 편리한 데카르트 좌표는 다음과 같은 짝수 순열에 의해 주어진다.[1]

  • (0, 0, ±φ)
  • (±1/2, ±φ/2, ±φ2/2)

여기서 φ은 황금비, 1 + √5/2이다.

이코시다케드론의 긴 반지름(중앙 대 정점)은 가장자리 길이에 대한 황금 비율이다. 따라서 가장자리 길이가 1이면 반지름이 φ이고, 가장자리 길이가 1이면 가장자리 길이가 1/2이다. 이 성질은 4차원 600세포, 3차원 이코시다데카헤드론, 2차원 데카곤 등 일부 균일한 폴리에스테르만이 갖고 있다. (이코시다데카헤드론은 600세포의 적도 단면이고, 데카곤은 이코시다데카헤드론의 적도 단면이다.) 반지름처럼 황금빛으로 빛나는 이 다각류는 중심에서 만나는 금빛 삼각형에서 각각 두 개의 반지름과 가장자리로 구성될 수 있다.

직교 투영

이코시다데카헤드론은 꼭지점, 가장자리, 삼각형, 오각형 얼굴을 중심으로 4개의 특별한 직교 돌출부를 가지고 있다. 마지막 두 개는 A와2 H Coxeter2 비행기에 해당한다.

직교 투영
중심: 꼭지점 가장자리 면
삼각형 		면
펜타곤
고체 Polyhedron 12-20 from blue max.png Polyhedron 12-20 from yellow max.png Polyhedron 12-20 from red max.png
와이어프레임 Dodecahedron t1 v.png Dodecahedron t1 e.png Dodecahedron t1 A2.png Dodecahedron t1 H3.png
투영적
대칭 		[2] [2] [6] [10]
이중 Dual dodecahedron t1 v.png Dual dodecahedron t1 e.png Dual dodecahedron t1 A2.png Dual dodecahedron t1 H3.png

표면 면적 및 부피

가장자리 길이 a의 iocsidodechedron의 표면 면적 A와 볼륨 V는 다음과 같다.

구면 타일링

60개의 가장자리는 구면 타일링에서 원형에 해당하는 6개의 데카곤을 형성한다.

이코시다데코헤드론은 구면 타일링으로도 표현될 수 있으며, 입체 투영을 통해 평면에 투영된다. 이 투영은 각도만 보존하고 면적이나 길이는 보존하지 않는다. 구의 직선은 평면에 원형 호로 투영된다.

Uniform tiling 532-t1.png Icosidodecahedron stereographic projection pentagon.png
펜타곤 중심 		Icosidodecahedron stereographic projection triangle.png
삼각형 중심
직교 투영법 입체 투영

관련 폴리토페스

이코시다데카헤드론은 교정된 도데카헤드론이고 또한 교정된 이코사헤드론이며, 이 일반 고형물들 사이에 완전한 가장자리 잘림으로 존재한다.

이코시다데카헤드론은 도데카헤드론의 5각형 12개와 이코사헤드론의 20개의 삼각형을 포함하고 있다.

균일한 이두면체 다면체 계열
대칭: [5,3], (*532) [5,3]+, (532)
Uniform polyhedron-53-t0.svg Uniform polyhedron-53-t01.svg Uniform polyhedron-53-t1.svg Uniform polyhedron-53-t12.svg Uniform polyhedron-53-t2.svg Uniform polyhedron-53-t02.png Uniform polyhedron-53-t012.png Uniform polyhedron-53-s012.png
CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node.png CDel node.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png CDel node.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node.pngCDel 3.pngCDel node 1.png CDel node 1.pngCDel 5.pngCDel node 1.pngCDel 3.pngCDel node 1.png CDel node h.pngCDel 5.pngCDel node h.pngCDel 3.pngCDel node h.png
{5,3} t{5,3} r{5,3} t{3,5} {3,5} rr{5,3} tr{5,3} sr{5,3}
이중에서 균일한 폴리헤드라까지
Icosahedron.jpg Triakisicosahedron.jpg Rhombictriacontahedron.jpg Pentakisdodecahedron.jpg Dodecahedron.jpg Deltoidalhexecontahedron.jpg Disdyakistriacontahedron.jpg Pentagonalhexecontahedronccw.jpg
V5.5.5 V3.10.10 V3.5.3.5 V5.6.6 V3.3.3.3.3 V3.4.5.4 V4.6.10 V3.3.3.3.5

이코시도데카헤드론은 정점 구성을 가진 퀘이레강 다면 및 틸팅의 일련의 대칭으로 존재하며,2 구의 기울기에서 유클리드 평면 및 쌍곡면으로 진행된다. *n32의 오비폴드 표기법 대칭에서 이러한 모든 기울기는 대칭의 기본 영역 내에서 와이오프 구조로 구성되며, 발전기 지점은 영역의 오른쪽 각도 모서리에 있다.[2][3]

*n32 quasiregular 틸팅의 궤도 대칭: (3.n)2
Quasiregular fundamental domain.png
건설 		구면 유클리드 주 쌍곡선
*332 *432 *532 *632 *732 *832... *∞32
퀘이레굴라속
수치 		Uniform tiling 332-t1-1-.png Uniform tiling 432-t1.png Uniform tiling 532-t1.png Uniform tiling 63-t1.svg Triheptagonal tiling.svg H2-8-3-rectified.svg H2 tiling 23i-2.png
꼭지점 (3.3)2 (3.4)2 (3.5)2 (3.6)2 (3.7)2 (3.8)2 (3.∞)2
*5n2 Quasiregular 틸팅의 대칭 돌연변이: (5.n)2
대칭
*5n2
[n,5] 		구면 쌍곡선 파라콤팩트 비컴팩트
*352
[3,5] 		*452
[4,5] 		*552
[5,5] 		*652
[6,5] 		*752
[7,5] 		*852
[8,5]... 		*∞52
[∞,5]
[ni,5]
수치 Uniform tiling 532-t1.png H2-5-4-rectified.svg H2 tiling 255-2.png H2 tiling 256-2.png H2 tiling 257-2.png H2 tiling 258-2.png H2 tiling 25i-2.png
구성 (5.3)2 (5.4)2 (5.5)2 (5.6)2 (5.7)2 (5.8)2 (5.∞)2 (5.ni)2
롬빅
수치 		Rhombictriacontahedron.jpg H2-5-4-rhombic.svg H2-5-4-primal.svg Order-6-5 quasiregular rhombic tiling.png
구성 V(5.3)2 V(5.4)2 V(5.5)2 V(5.6)2 V(5.7)2 V(5.8)2 V(5.219) V(5.219)

해부

이코시다데카헤드론은 거울 이미지로 연결된 두 오각형 로툰대에 의해 만들어진 오각형 오각형 오각형 오각형 오각형 로툰다라고 불리는 존슨 고체와 관련이 있다. 따라서 이코시도데카헤드론은 위와 아래가 반반인 오각형 자이로비로툰다라고 불릴 수 있다.

Dissected icosidodecahedron.png
(해부)
Icosidodecahedron.png
이코시다데카헤드론
(자이로비로툰다)
Pentagonal orthobirotunda solid.png
오각형 오르토비 로툰다
Pentagonal rotunda.png
오각형 로툰다

관련 다면체

잘린 큐브에 있는 이코시다데카헤드론

잘린 정육면체는 옥타곤을 오각형 2개와 삼각형 2개로 나눠 이코시다데카헤드론으로 바꿀 수 있다. 그것은 화두 대칭을 가지고 있다.

8개의 균일한 항성 다면체는 같은 꼭지점 배열을 공유한다. 이 중 두 개의 가장자리 배열도 같다: 작은 이코시헤미도데카헤메드론(삼각형 면을 공통으로 함)과 작은 도데카헤미도데카헤메드론(오각형 얼굴을 공통으로 함)이다. 정점 배치는 5옥타헤드라와 5옥타헤미헥사헤드라의 화합물과도 공유된다.

Icosidodecahedron.png
이코시다데카헤드론 		Small icosihemidodecahedron.png
소이코시헤미도데코헤드론 		Small dodecahemidodecahedron.png
소도데카헤미도데코헤드론
Great icosidodecahedron.png
대이코시다데카헤드론 		Great dodecahemidodecahedron.png
대 도데카헤미도데코헤드론 		Great icosihemidodecahedron.png
대이코시헤미도데코헤드론
Dodecadodecahedron.png
도데카데카헤드론 		Small dodecahemicosahedron.png
작은 도데카헤미코사헤드론 		Great dodecahemicosahedron.png
도데카헤미코사헤드론
Compound of five octahedra.png
5옥타헤드라 화합물 		UC18-5 tetrahemihexahedron.png
5개의 테트라헤미헥사헤드라의 화합물

관련 폴리초라

4차원 기하학에서 아이코시다데커헤드론은 일반 600셀에서 600셀에서 3D 공간을 통과하는 600셀의 정점 첫 번째 통로에 속하는 적도 슬라이스로 나타난다. 즉, 600 셀의 30 정점들은 정점 쌍으로부터 그것의 한정된 하이퍼피어의 원호 거리 90도에 놓여있고, 이코시다데카헤드론의 정점이다. 600 셀의 와이어 프레임 수치는 72개의 평평한 일반 디카곤으로 구성되어 있다. 이 중 6개는 정점 쌍에 대한 적도 디카곤이다. 그것들은 정확히 이코시다데카헤드론의 철조망을 이루는 6개의 디카곤이다.

이코시다데카헤드랄 그래프

이코시다데카헤드랄 그래프
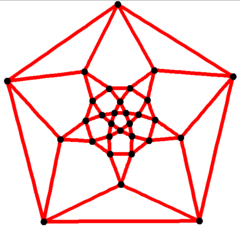Icosidodecahedral graph.png
5배 대칭 슐레겔 도표
정점30
가장자리60
자동형성120
특성.쿼틱 그래프, 해밀턴 그래프, 정규 그래프
그래프 및 모수 표

그래프 이론의 수학적 분야에서, iocsiddodechedral 그래프는 아르키메데스 고형물 중 하나인 iocsiddecahedron의 정점과 가장자리를 그래프로 나타낸 것이다. 정점 30개와 가장자리 60개를 가지고 있으며, 4분위 그래프 아르키메데스 그래프 입니다.[4]

트리비아

스타트랙유니버스에서는 논리 칼토(Kal-Toh)의 벌컨 게임이 홀로그램 아이코시다데카헤드론을 만드는 것을 목표로 하고 있다.

<오행성> 시리즈 중 1편을 팀 프랫이 쓴 <오행성>에서 엘레나는 그녀의 양쪽에 이코시다데카헤드론 기계가 있다.[종이백 p 336]

호베르만 구는 이코시다데카헤드론이다.

Icosidodecahedra는 인간 세포를 포함한 모든 진핵 세포에서 13/31 COPIII 코팅 단백질 형성으로 발견될 수 있다. [5]

참고 항목

메모들

  1. ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
  2. ^ Coxeter 일반 폴리토페스, 제3판, (1973) 도버판, ISBN 0-486-61480-8 (V장: 칼리도스코프, 섹션: 5.7 와이토프의 건설)
  3. ^ 대니얼 허슨의 2차원 대칭 돌연변이
  4. ^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
  5. ^ Russell, Christopher; Stagg, Scott (11 February 2010). "New Insights into the Structural Mechanisms of the COPII Coat". Traffic. 11 (3): 303–310. doi:10.1111/j.1600-0854.2009.01026.x. PMID 20070605.

참조

  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
  • Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

외부 링크