핵융합

이 기사에 열핵융합을 포함시킬 것을 제안했다.(논의) 2022년 6월부터 제안.

핵물리학
핵·핵자(p, n)·핵물질·핵력·핵구조·핵반응
핵 모형 액체 방울 · 핵셸 모형 · 상호작용 보손 모형 · Ab initio
핵종 분류 동위원소 – Z 등가 Isobars – 동등 A 아이소톤 – N 등가 Isodiaphers – 동일 N - Z 이성질체 – 위의 모든 것과 동일 거울핵 – Z ↔ N 안정·매직·짝수/홀수·헤일로(보롬어)
핵안정성 결합 에너지 · p-n비 · 드립 라인 · 안정의 섬 · 안정의 계곡 · 안정 핵종
방사성 붕괴 알파α·베타β(2β(0v, β+)·K/L포착·이성질체(감마δ·내부 변환)·순간 핵분열·클러스터 붕괴·중성자 방출·프로톤 방출 붕괴 에너지 · 붕괴사슬 · 붕괴 생성물 · 방사성 핵종
핵분열 자발적·제품(페어 브레이킹)·사진
프로세스 캡처 전자(2×) · 중성자(s · r) · 양성자(p · rp)
고에너지 프로세스 파쇄(우주선에 의한) · 광집적
핵합성 및 핵천체물리학 핵융합 프로세스:스타·빅뱅·초신성 핵종 : 원시·코스모제닉·인공
고에너지 핵물리학 쿼크-글루온 플라즈마 · 오른쪽 · LHC
과학자 알바레즈 · 베크렐 · 베테 · A. 보어 · N. 보어 · 채드윅 · 콕크로프트 · 퀴리 · 퀴리 부인 · 파이 퀴리 · 스크워도프스카 퀴리 · 데이비슨 · 페르미 · 한 · 젠센 · 로렌스 · 메이어 · 마이트너 · 올리판트 · 오펜하이머 · 프로카 · 퍼셀 · 라비 · 러더퍼드 · 소디 · 스트라스만 · 【Wiąteckckckckte】 · 실라드 · 텔러 · 톰슨 · 월튼 · 위그너
물리 포털 카테고리
v t

핵융합은 두 개 이상의 원자핵이 하나 이상의 다른 원자핵과 아원자 입자(중성자 또는 양성자)를 형성하기 위해 결합되는 반응이다.반응물과 생성물 사이의 질량 차이는 에너지의 방출 또는 흡수로 나타난다.이 질량의 차이는 반응 전후에 원자핵 사이의 핵결합 에너지의 차이로 인해 발생한다.핵융합은 활성 또는 주계열성 및 다른 고등급 별에 전력을 공급하는 과정으로, 많은 양의 에너지가 방출됩니다.

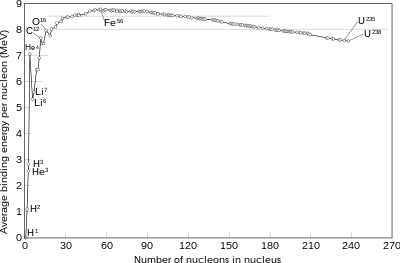
철-56이나 니켈-62보다 가벼운 원자핵을 생성하는 핵융합 과정은 일반적으로 에너지를 방출할 것이다.이 원소들은 핵자당 비교적 작은 질량과 상대적으로 큰 결합 에너지를 가지고 있다.이것보다 가벼운 핵의 융합은 에너지를 방출하는 반면, 무거운 핵의 융합은 생성물 핵에 의해 유지되는 에너지를 발생시키고, 그 결과 발생하는 반응은 흡열성입니다.핵분열이라고 불리는 그 반대의 과정에서는 그 반대입니다.핵융합은 일반적으로 더 용융성이 높은 수소나 헬륨과 같은 가벼운 원소를 사용하는 반면 우라늄, 토륨, 플루토늄과 같은 무거운 원소는 더 핵분열성이 높다.초신성의 극단적인 천체물리학적 사건은 원자핵을 철보다 무거운 원소로 융합할 수 있는 충분한 에너지를 만들어 낼 수 있다.

역사

1920년, 아서 에딩턴은 수소-헬륨 융합이 항성 에너지의 주요 원천일 수 있다고 제안했다.양자 터널링은 1929년 Friedrich Hund에 의해 발견되었고, 곧이어 Robert Atkinson과 Fritz Houtermans는 작은 핵을 융합함으로써 많은 양의 에너지가 방출될 수 있다는 것을 보여주기 위해 측정된 질량의 광원소를 사용했다.패트릭 블래킷의 인공 핵변환 초기 실험을 바탕으로 1932년 마크 올리펀트에 의해 수소 동위원소의 실험실 핵융합이 이루어졌다.그 후 10년 동안 별의 핵융합 주기에 대한 이론은 한스 베테에 의해 고안되었다.군사 목적의 핵융합 연구는 맨해튼 프로젝트의 일환으로 1940년대 초에 시작되었다.자생 핵융합은 1952년 11월 1일 아이비 마이크 수소(열핵) 폭탄 실험으로 처음 수행되었다.

핵융합로 내부의 제어된 핵융합 개발에 대한 연구는 1940년대부터 진행되어 왔지만, 그 기술은 아직 개발 단계에 있다.

과정

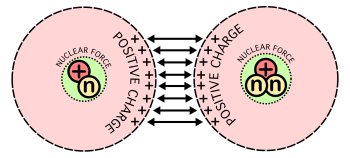
가벼운 원소의 융합으로 에너지가 방출되는 것은 두 개의 반대되는 힘, 즉 양성자와 중성자를 결합하는 핵력과 양성자가 서로를 밀어내는 쿨롱력의 상호작용 때문이다.양성자는 양전하를 띠고 쿨롱 힘에 의해 서로 밀어내지만, 그럼에도 불구하고 서로 달라붙을 수 있으며,^[2] 핵흡인력으로 불리는 또 다른 단거리 힘의 존재를 보여준다.가벼운 핵(또는 철과 니켈보다 작은 핵)은 충분히 작고 양성자가 부족하여 핵력이 반발을 극복할 수 있다.이것은 핵이 충분히 작기 때문에 모든 핵자는 적어도 무한 범위 쿨롱의 반발을 느끼는 것만큼 강한 단거리 유인력을 느끼기 때문입니다.핵융합을 통해 더 가벼운 핵에서 핵을 만드는 것은 입자의 순수 인력으로부터 여분의 에너지를 방출한다.그러나 더 큰 핵의 경우, 핵력은 단거리이고 더 긴 핵 길이 척도에 걸쳐 계속 작용할 수 없기 때문에 에너지가 방출되지 않는다.따라서 에너지는 그러한 핵의 융합과 함께 방출되지 않고 대신 그러한 과정을 위한 입력으로 에너지가 필요하다.

핵융합은 별에 힘을 실어주고 핵합성이라고 불리는 과정에서 사실상 모든 원소를 생산한다.태양은 주계열성이기 때문에 수소핵을 헬륨으로 핵융합함으로써 에너지를 발생시킨다.태양은 중심핵에서 6억 2천만 미터톤의 수소를 융합하고 초당 6억 1천 6백만 미터톤의 헬륨을 생산한다.별에서 가벼운 원소들의 융합은 에너지와 그에 수반되는 질량을 방출합니다.예를 들어, 헬륨을 형성하기 위한 두 수소핵의 융합에서 질량의 0.645%는 알파 입자의 운동 에너지 또는 전자파 ^[3]방사선과 같은 다른 형태의 에너지의 형태로 운반된다.

가장 가벼운 원소인 수소도 핵을 강제로 융합시키려면 상당한 에너지가 필요합니다.충분한 속도로 가속되면, 핵은 이러한 정전기적 반발을 극복할 수 있고, 끌리는 핵력이 반발하는 쿨롱 힘보다 클 정도로 충분히 가까이 다가갈 수 있다.강한 힘은 일단 핵이 충분히 가까워지면 빠르게 증가하며, 융합하는 핵자는 본질적으로 서로 "떨어질" 수 있고 그 결과는 핵융합과 순 에너지로 생산된다.더 무거운 핵과 종종 자유 중성자 또는 양성자를 만드는 가벼운 핵의 융합은 일반적으로 핵을 함께 만드는 데 필요한 것보다 더 많은 에너지를 방출한다; 이것은 자생적인 반응을 일으킬 수 있는 발열 과정이다.

대부분의 핵 반응에서 방출되는 에너지는 화학 반응에서보다 훨씬 더 크다. 왜냐하면 핵을 함께 고정시키는 결합 에너지는 전자를 핵에 고정시키는 에너지보다 더 크기 때문이다.예를 들어 수소핵에 전자를 첨가하여 얻은 이온화 에너지는 13.6eV로, 인접한 도표에 나타난 중수소-삼중수소(D–T) 반응에서 방출된 17.6MeV의 100만분의 1에도 미치지 못한다.핵융합 반응은 핵분열보다 몇 배 더 큰 에너지 밀도를 가지고 있다; 개별 핵분열 반응이 일반적으로 화학 반응보다 수백만 배 더 강력한 개별 핵융합 반응보다 훨씬 더 많은 에너지를 생성한다.물질과 반물질의 전멸적 충돌에 의해 일어나는 것과 같은 질량의 직접적인 에너지 변환만이 핵융합보다 질량 단위당 더 에너지적이다.(1그램의 물질을 완전히 변환하면 9×10줄의¹³ 에너지가 방출됩니다.)

전력 생산에 핵융합 기술을 사용하는 연구는 60년 이상 지속되어 왔다.현재의 기술(예: 퓨저)로 일반적으로 제어 핵융합이 가능하지만, 성공적인 경제 핵융합 달성은 과학적,^[which?] 기술적 어려움으로 인해 좌절되어 왔다. 그럼에도 불구하고, 중요한 진전이 이루어졌다.현재 제어된 핵융합 반응은 손익분기점(자생적) 제어된 ^[4]핵융합 효과를 낼 수 없었다.이를 위한 가장 발전된 두 가지 접근법은 자기 구속(트로이드 설계)과 관성 구속(레이저 설계)이다.

플라즈마를 필요한 온도로 가열하는 데 필요한 양의 10배 이상의 핵융합 에너지를 이론적으로 전달하는 트로이덜 원자로에 대한 실행 가능한 설계가 개발 중입니다(ITER 참조).ITER 시설은 2025년에 완공될 예정이다.같은 해 원자로 가동에 들어가 2025년 플라즈마 실험을 시작할 예정이지만 2035년이 돼야 완전한 중수소-삼중수소 융합이 시작될 것으로 예상된다.^[5]

마찬가지로 캐나다에 본부를 둔 General Fusion은 자화 표적 핵융합 에너지 시스템을 개발하고 ^[6]있으며 2025년까지 시범 발전소를 건설하는 것을 목표로 하고 있다.

레이저 구동식 관성 구속 융합을 사용하는 US National Ignition Facility는 손익분기점 융합을 목표로 설계되었으며, 최초의 대규모 레이저 표적 실험은 2009년 6월에 수행되었고,^[7][8] 점화 실험은 2011년 초에 시작되었다.

의

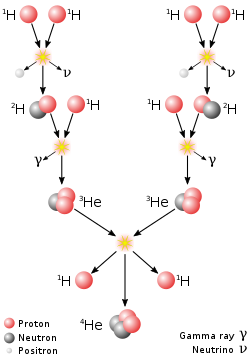
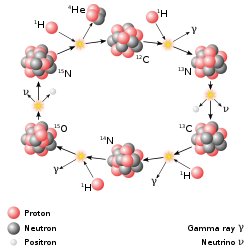
중요한 핵융합 과정은 태양을 포함한 별들을 움직이는 별의 핵합성이다.20세기에는 핵융합 반응에서 방출되는 에너지가 별의 열과 빛의 수명을 설명하는 것으로 인식되었다.별의 핵융합은 초기 수소와 헬륨의 풍부함에서 시작하여 에너지를 제공하고 새로운 핵을 합성합니다.별의 질량(따라서 중심부의 압력과 온도)에 따라 다른 반응 사슬이 관여합니다.

1920년경, Arthur Eddington은 그의 논문 The Internal Configuration of the ^[9][10]Stars에서 별에서 핵융합 과정의 발견과 메커니즘을 예측했다.그 당시 별의 에너지원은 완전히 미스터리였다. 에딩턴은 아인슈타인의 방정식 E = mc에² 따라 엄청난 에너지를 방출하면서 수소를 헬륨으로 융합시켰다고 정확하게 추측했다.이것은 그 당시 핵융합과 열핵 에너지가 아직 발견되지 않았고 심지어 별들이 대부분 수소로 이루어져 있기 때문에 특히 주목할 만한 발전이었다.에딩턴의 논문은 다음과 같이 추론했다.

1. 항성에너지에 대한 주도적인 이론인 수축 가설은 각운동량 보존으로 인해 항성의 자전 속도가 눈에 띄게 빨라지게 할 것입니다.그러나 세페이드 변광성을 관측한 결과 이런 일이 일어나지 않았다.
2. 유일하게 그럴듯한 에너지원으로 알려진 것은 물질을 에너지로 바꾸는 것이었다; 아인슈타인은 몇 년 전에 적은 양의 물질이 많은 양의 에너지와 동등하다는 것을 보여주었다.
3. 프란시스 애스턴은 또한 헬륨 원자의 질량이 헬륨 원자를 형성할 4개의 수소 원자의 질량보다 약 0.8% 적다는 것을 최근에 보여주었다. (당시 원자량이 원소 사이의 구별되는 특성으로 유지되었던 원자 구조의 지배적인 이론에 따르면; 헨리 모즐리와 안토니우스 반 d에 의해 연구되었다.엥 브로크는 나중에 핵 전하가 구별되는 특성이고 따라서 헬륨 핵이 두 개의 수소 핵과 추가 질량으로 구성되어 있다는 것을 보여줄 것이다.이는 그러한 결합이 발생할 수 있다면 상당한 에너지를 부산물로 방출할 것임을 시사했다.
4. 의 '가 5%되어 있다는 것을 우리는 있다(우리는 이제 대부분의 '보통' 별들이 5% 이상의 수소를 함유하고 있다는 것을 알고 있습니다.)
5. 더 많은 원소들이 융합될 수도 있고, 다른 과학자들은 별들이 가벼운 원소들이 합쳐져 무거운 원소들을 만들어내는 "잔혹성"이라고 추측했지만, 그들의 원자 질량을 더 정확하게 측정하지 않으면 그 당시에 더 이상 말할 수 없었다.

이 모든 추측은 이후 수십 년 동안 옳았다는 것이 입증되었다.

태양 에너지와 비슷한 크기의 별들의 주요 원천은 수소가 헬륨을 형성하기 위해 융합하는 것입니다. 헬륨은 태양 중심 온도 1400만 켈빈에서 발생합니다.최종 결과는 네 개의 양성자가 하나의 알파 입자로 융합되고, 두 개의 양자와 두 개의 중성미자가 방출되며, 그리고 에너지가 방출됩니다.무거운 별에서는 CNO 순환과 다른 과정이 더 중요합니다.별은 수소의 상당 부분을 소모하면서 무거운 원소들을 합성하기 시작합니다.가장 무거운 원소들은 더 무거운 별이 수명이 다한 후에 초신성 핵합성이라고 알려진 과정인 격렬한 초신성을 겪을 때 일어나는 핵융합에 의해 합성된다.

융접이 발생하기 전에 정전력의 상당한 에너지 장벽을 극복해야 합니다.원거리에서는 양전하를 띤 양성자 사이의 반발 정전기력 때문에 두 개의 벗은 핵이 서로를 밀어냅니다.하지만 두 개의 핵이 충분히 가까이 다가갈 수 있다면, 정전기적 반발은 핵이 쿨롱 힘을 통해 터널을 뚫을 수 있는 양자 효과에 의해 극복될 수 있다.

양성자나 중성자와 같은 핵자가 핵에 추가되면, 핵력은 핵의 다른 모든 핵자로 끌어당긴다(원자가 충분히 작은 경우). 그러나 주로 힘의 범위가 짧기 때문에 핵의 바로 옆 핵자로 끌어당긴다.핵 내부의 핵자는 표면에 있는 핵자보다 더 많은 인접 핵자를 가지고 있다.작은 핵은 표면적 대 부피비가 크기 때문에 핵력에 의한 핵자당 결합 에너지는 일반적으로 핵의 크기에 따라 증가하지만 지름 약 4개의 핵자에 대응하는 한계치에 근접한다.핵자는 양자 물체라는 것을 명심하는 것이 중요하다.따라서 예를 들어 핵에 있는 두 중성자는 서로 동일하기 때문에 어떤 중성자가 내부에 있고 어떤 중성자가 표면에 있는지를 구별하는 목표는 사실상 무의미하며 따라서 양자역학의 포함은 적절한 계산을 위해 필요합니다.

반면 정전기력은 역제곱력이기 때문에 핵에 추가된 양성자는 핵에 있는 다른 모든 양성자로부터 정전기적 반발을 느낄 것이다.따라서 정전기력으로 인한 핵자당 정전기 에너지는 원자번호가 증가함에 따라 무제한으로 증가한다.

정전기력과 강한 핵력의 최종 결과는 일반적으로 크기가 커짐에 따라 핵자당 결합 에너지가 철과 니켈 원소까지 증가하며, 더 무거운 핵자에 대해서는 감소하는 것입니다.결국 결합 에너지는 음이 되고 매우 무거운 핵자(모두 208개 이상의 핵자를 가지고 있으며, 직경은 약 6개입니다)는 안정적이지 않습니다.Ni, Fe, Fe
, Fe, ^[11]Ni가

핵자당 결합 에너지가 감소하는 순서로 가장 단단하게 결합된 4개의 핵이다
.니켈 동위원소인
Ni가 더 안정적이지만, 철 동위원소
Fe가 더 흔하다.이것은 별이 알파 과정을 통해 Ni를 만드는
쉬운 방법이 없기 때문입니다.

이러한 일반적인 추세의 예외는 헬륨-4 핵으로, 헬륨-4 핵의 결합 에너지는 다음으로 무거운 원소인 리튬보다 높다.이것은 양성자와 중성자가 페르미온이기 때문에 파울리 배타 원리에 따르면 정확히 같은 상태의 동일한 핵에 존재할 수 없습니다.핵에서 각 양성자 또는 중성자의 에너지 상태는 스핀업 입자와 스핀다운 입자를 모두 수용할 수 있습니다.헬륨-4의 핵은 두 개의 양성자와 두 개의 중성자로 구성되어 있기 때문에 비정상적으로 큰 결합 에너지를 가지고 있다. 그래서 헬륨-4의 핵자는 모두 지면 상태에 있을 수 있다.추가 핵자는 더 높은 에너지 상태로 들어가야 합니다.실제로 헬륨-4 핵은 핵물리학에서 단일 양자역학 입자, 즉 알파 입자로 취급될 정도로 단단하게 묶여 있다.

두 개의 핵이 합쳐지면 상황은 비슷하다.서로 다가갈 때, 한 핵에 있는 모든 양성자가 다른 핵에 있는 모든 양성자를 밀어냅니다.두 개의 핵이 실제로 충분히 오랫동안 충분히 가까워질 때까지 강한 핵력이 (터널링을 통해) 극복할 수 있는 반발성 정전기력이다.따라서 최종 에너지 상태가 낮아도 먼저 극복해야 할 큰 에너지 장벽이 있습니다.그것은 쿨롱 장벽이라고 불린다.

쿨롱 장벽은 수소 동위원소의 핵이 단 하나의 양전하를 포함하고 있기 때문에 가장 작다.다이프로톤은 안정적이지 않기 때문에 중성자 또한 매우 엄격한 결합을 가진 헬륨 핵이 생성물 중 하나가 되도록 관여해야 합니다.

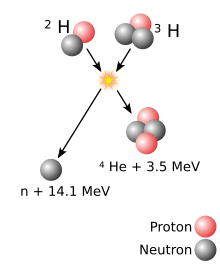
중수소-삼중수소 연료를 사용하면 에너지 장벽은 약 0.1MeV이다.이에 비해 수소로부터 전자를 제거하는 데 필요한 에너지는 13.6eV이다.융합의 (중간) 결과는 불안정한 He 핵으로, 14.1 MeV의 중성자를 즉시 방출한다.나머지 He핵의 반동에너지는 3.5MeV이므로 방출되는 총 에너지는 17.6MeV입니다.이는 에너지 장벽을 극복하는 데 필요한 것보다 몇 배나 많은 양입니다.

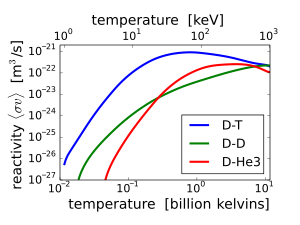
반응 단면(θ)은 두 반응물 핵의 상대 속도 함수로써 핵융합 반응의 확률을 측정하는 것이다.반응물이 속도 분포(예: 열 분포)를 갖는 경우 단면적 및 속도의 곱 분포에 대해 평균을 수행하는 것이 유용합니다.이 평균은 '반응성'이라고 불리며 'v'로 표기됩니다.반응 속도(시간당 부피당 융합)는 반응물 수 밀도의 곱의 "v"배입니다.

$f vdisplaystyle f=n_{1}n_{2}\classle \class v\rangle .}$

DD 반응과 같이 핵종이 자신과 같은 핵과 반응하는 경우 ${\displaystyle {}_{}{}_{}}$ $({$ style $n_{1}n_{2})$는 ${\displaystyle n2\mathrm{}{}^{}}$2$({display style$ n$^{2}/2$로 $대체$되어야 한다.

${\displaystyle }$§ $（$ \$displaystyle$ \$langle$ \ $sigma v$ \ rangle$）$는 실온에서 사실상 0에서 10 ~100 keV의 온도에서 유의한 크기로 증가합니다${\displaystyle .}$일반적인 이온화 에너지(수소의 경우 13.6 eV)를 훨씬 상회하는 온도에서 핵융합 반응물은 플라즈마 상태로 존재한다.

특정 에너지 구속시간을 갖는 장치에서의 온도 함수로서의 $⟨{\displaystyle }$ v ${\displaystyle \sigma }$ v$${\ \ $displaystyle \langle$ \$sigma v$\rangle$$}의$$ 의의는 Lawson 기준을 고려하여 구한다.이것은 지구상에서 극복하기에 매우 어려운 장벽이며, 이것이 핵융합 연구가 현재의 진보된 ^[12]기술 상태에 도달하는 데 많은 시간이 걸린 이유를 설명해준다.

물질이 충분히 가열되고(그래서 플라즈마인 경우), 입자의 극도의 열운동 에너지와의 충돌로 인해 핵융합 반응이 발생할 수 있습니다.열핵 무기는 핵융합 에너지의 통제되지 않은 방출에 상당하는 양을 생산한다.제어된 열핵융합 개념은 플라즈마를 제한하기 위해 자기장을 사용한다.

관성 구속 융합(ICF)은 연료 표적(일반적으로 중수소와 삼중수소가 포함된 펠릿)을 가열하고 압축하여 핵융합 에너지를 방출하는 것을 목표로 하는 방법이다.

관성 정전 제한은 전계를 사용하여 이온을 핵융합 조건으로 가열하는 장치 세트입니다.가장 잘 알려진 것은 퓨저입니다.1999년부터 많은 아마추어들이 이러한 사제 ^{[13][14][15][16]}장치를 사용하여 아마추어 퓨전을 할 수 있게 되었다.기타 IEC 디바이스에는 Polywell,^[18] MIX^[17] POPS 및 Marble 개념이 있습니다.

빔-빔 또는 빔-타겟 융접

가속기 기반 광이온 핵융합은 광이온 핵융합 반응을 유도하기에 충분한 입자 운동 에너지를 얻기 위해 입자 가속기를 사용하는 기술이다.광이온 가속은 비교적 쉽고 효율적인 방법으로 수행할 수 있습니다. 진공관, 한 쌍의 전극 및 고전압 변압기만 있으면 됩니다. 전극 사이에 10kV만 있으면 융접을 관찰할 수 있습니다.이 시스템은 이온을 빔-타겟 융접이라고 하는 정적 연료 주입 타깃으로 가속화하거나 두 이온 스트림을 서로 향해 가속하여 빔-빔 융접으로 가속화하도록 배열할 수 있습니다.

가속기 기반 융접(및 일반적으로 콜드 타깃)의 주요 문제는 융접 단면이 쿨롱 상호 작용 단면보다 훨씬 낮다는 것이다.따라서 대부분의 이온은 에너지를 방출하여 대상 원자의 이온화를 방출한다.밀폐관 중성자 발생기라고 하는 장치는 특히 이 논의와 관련이 있다.이러한 소형 장치는 수소화물 표적에 대해 이러한 핵의 이온이 가속될 수 있도록 하는 배열로 중수소와 삼중수소 가스로 채워진 소형 입자 가속기이며, 핵융합이 일어나 중성자 플럭스를 방출하는 중수소와 삼중수소를 포함한다.석유 산업에서 사용하기 위해 매년 수백 개의 중성자 발생기가 생산되며, 이 중성자 발생기는 석유 매장량을 찾고 매핑하기 위한 측정 장비에 사용됩니다.

"누락된" 충돌로 인해 이온을 재순환하려는 여러 시도가 수년간 이루어졌습니다.1970년대에 가장 잘 알려진 시도 중 하나는 미그마로, 독특한 입자 저장 고리를 사용하여 이온을 원형 궤도로 잡아 반응 영역으로 되돌렸다.이론적 계산 자금 검토 중에 이루어진 시스템이 중요한 난이도가 힘의 원천으로서 상관이 있는 충분한 핵 융합 연료를 채우도록 규모를 가질 것이라고 지적했다.1990년대에, 새로운 협정은 저장 시스템으로field-reverse 구성(FRC)를 사용하여 노먼 Rostoker에 의해 태광에 의한 2021[업데이트]의 공부를 계속해서 제안되었다.밀접하게 관련 접근 방식은 적극적으로 엘리옹 에너지 연구 대상이 되고 맞은 편에 있directions,[19]에 두 FRC의 회전하는 합칠 수 있다.왜냐하면 이러한 접근 방식 모두가 쿨롱 장벽을 뛰어넘어 이온 에너지를 갖고 있기 때문에 종종 p-11B 같은 대체 연료 주기의 너무 관습적인 방법들을 시도하기 어려운 사용을 제안한다.[20]

뮤온 촉매 융합

뮤온 촉매 융합은 상온에서 일어나는 융합 과정이다.그것은 1980년대 초에 스티븐 존스에 의해 자세히 연구되었다.뮤온 생성에 필요한 높은 에너지, 짧은 2.2µ의 반감기, 뮤온이 새로운 알파 입자에 결합하여 융합 ^[21]촉매를 멈출 가능성이 높기 때문에 이 반응에서 발생하는 순 에너지 생산은 성공하지 못했습니다.

기타 원칙

몇몇 다른 감금 원칙들이 조사되었다.

• 반물질 초기 핵융합은 작은 핵융합 폭발을 일으키기 위해 소량의 반물질을 사용한다.이는 주로 핵펄스 추진과 순수 핵융합 폭탄을 실현 가능하게 하는 맥락에서 연구되어 왔다.이것은 반물질 제조 비용만으로는 실질적인 동력원이 될 수 없습니다.
• UCLA의 한 팀에 의해 2005년 4월에 열전 핵융합이 보고되었다.과학자들은 -34~7°C(-29~45°F)로 가열된 열전 결정을 텅스텐 바늘과 결합하여 약 25기가볼트의 전장을 만들어 중수소 핵을 이온화하고 중수소화물 표적으로 가속시켰다.추정된 에너지 ^[22]수준에서 D-D 핵융합 반응이 일어나 헬륨-3과 2.45 MeV 중성자가 생성될 수 있다.비록 유용한 중성자 발생기를 만들지만,^{[23][24][25][26]} 이 장치는 생산되는 것보다 훨씬 더 많은 에너지를 필요로 하기 때문에 발전용으로 만들어지지 않았다.D-T 핵융합 반응은 삼중수소 엘비움 ^[27]표적에서 관찰되었다.
• 하이브리드 핵융합-분열(하이브리드 핵발전)은 핵융합과 핵분열 과정의 조합을 사용하여 전력을 생산하는 제안된 방법이다.이 개념은 1950년대로 거슬러 올라가 1970년대에 한스 베테가 잠시 주창했지만 순수 ^[28]핵융합 실현이 지연되면서 2009년에 관심이 되살아날 때까지 대부분 연구되지 않았다.
• 1970년대 중반 로스앨러모스 국립연구소(LANL)에서 실시된 PACER 프로젝트는 지하 공동 안에서 소형 수소폭탄(융합폭탄)을 폭발시키는 핵융합 발전 시스템의 가능성을 탐색했다.에너지원으로서 이 시스템은 기존 기술을 사용하여 작동한다는 것을 입증할 수 있는 유일한 핵융합 전력 시스템입니다.그러나 그것은 또한 크고 지속적인 핵폭탄의 공급을 필요로 할 것이고, 그러한 시스템의 경제성을 다소 의심스럽게 만들 것이다.
• 소노퓨전이라고도 불리는 버블융합은 2000년대 초에 두드러졌던 소닉 캐비테이션을 통한 융합을 이루기 위한 제안 메커니즘이었다.이후 복제 시도는 실패했고 수석 조사관인 Rusi Talyarkhan은 2008년 ^[29]연구 부정행위로 유죄 판결을 받았다.

중요한 반응

별의 반응 사슬

항성핵의 온도와 밀도에서는 핵융합 반응 속도가 느리기로 악명 높다.예를 들어, 태양 코어 온도(T ≤ 15 MK)와 밀도(160 g/cm³)에서 에너지 방출 속도는 276 μW/cm에³ 불과하며, 이는 정지해 있는 인체가 ^[30]열을 발생시키는 체적 속도의 약 4분의 1이다.따라서 핵융합 발전용 실험실에서 별의 핵융합 상태를 재현하는 것은 완전히 비현실적이다.핵반응 속도는 온도뿐만 아니라 밀도에 따라 달라지고 대부분의 핵융합 방식은 비교적 낮은 밀도로 작동하기 때문에 이러한 방법은 높은 온도에 크게 의존한다.온도(exp(-E/kT)의 함수로서의 핵융합 속도는 항성 내부 온도보다 10-100배 높은 지상 원자로 온도를 달성해야 한다.T 0 0.1 ~ 1.0 × 10⁹ K.

지상반응의 기준 및 후보

인공 핵융합에서는 1차 연료가 양성자로 제한되지 않고 고온을 사용할 수 있으므로 단면이 큰 반응이 선택된다.또 다른 우려 사항은 원자로 구조를 방사적으로 활성화하는 중성자의 생산이지만, 핵융합 에너지와 삼중수소 증식을 체적 추출할 수 있다는 장점이 있다.중성자를 방출하지 않는 반응을 부류전자라고 합니다.

유용한 에너지원이 되려면 핵융합 반응이 몇 가지 기준을 충족해야 합니다.다음 조건을 충족해야 합니다.

발열하다

이것은 결합 에너지 곡선의 낮은 Z(양자 수) 쪽으로 반응 물질을 제한합니다.이것은 또한 헬륨
He를 매우 단단하게 결합하기 때문에 가장 일반적인 제품으로 만들기도 하지만
He와
H도 나타납니다.

낮은 원자 번호(Z) 핵 포함

이것은 핵이 융합할 만큼 가까이 있기 전에 극복해야 하는 정전적 반발이 핵이 포함하는 양성자의 수, 즉 원자 ^{[citation needed]}번호와 직접적으로 관련이 있기 때문입니다.

반응물이 2개 있다.

별의 밀도보다 작은 어떤 것에서도, 3체 충돌은 너무 일어날 것 같지 않다.관성 구속에서 별의 밀도와 온도는 모두 ICF의 매우 짧은 구속 시간인 로슨 기준의 세 번째 매개변수의 단점을 보완하기 위해 초과된다.

2개 이상의 제품을 가지고 있다

이를 통해 전자기력에 의존하지 않고 에너지와 운동량을 동시에 보존할 수 있습니다.

양성자와 중성자 모두 보존

약한 교호작용에 대한 단면이 너무 작습니다.

이러한 기준을 충족하는 반응은 거의 없습니다.단면이 ^[31]가장 큰 것은 다음과 같습니다.

(1)

2 1D .

+

3 1T .

→

4 2그는

(

3.52 MeV

)

+

n0

(

14.06 MeV

)

(2i)

2 1D .

+

2 1D .

→

3 1T .

(

1.01 MeV

)

+

p+.

(

3.02 MeV

)

50%

(2ii)

→

3 2그는

(

0.82 MeV

)

+

n0

(

2.45 MeV

)

50%

(3)

2 1D .

+

3 2그는

→

4 2그는

(

3.6 MeV

)

+

p+.

(

14.7 MeV

)

(4)

3 1T .

+

3 1T .

→

4 2그는

+

2n0

+

11.3 MeV

(5)

3 2그는

+

3 2그는

→

4 2그는

+

오후 2시+

+

12.9 MeV

(6i)

3 2그는

+

3 1T .

→

4 2그는

+

p+.

+

n0

+

12.1 MeV

57%

(6ii)

→

4 2그는

(

4.8 MeV

)

+

2 1D .

(

9.5 MeV

)

43%

(7i)

2 1D .

+

6 3리

→

2 4 2He

+

22.4 MeV

(7ii)

→

3 2그는

+

4 2그는

+

n0

+

2.56 MeV

(7iii)

→

7 3리

+

p+.

+

5.0 MeV

(7iv)

→

7 4있다

+

n0

+

3.4 MeV

(8)

p+.

+

6 3리

→

4 2그는

(

1.7 MeV

)

+

3 2그는

(

2.3 MeV

)

(9)

3 2그는

+

6 3리

→

2 4 2He

+

p+.

+

16.9 MeV

(10)

p+.

+

11 5B .

→

3 4 2He

+

8.7 MeV

핵합성
별의 핵합성 빅뱅 핵합성 초신성 핵합성 우주선 파쇄
관련 토픽
천체 물리학 핵융합 R프로세스 S프로세스 핵분열
v t

두 생성물과의 반응의 경우, 에너지는 그림과 같이 질량에 반비례하여 두 생성물 간에 분배됩니다.세 가지 제품을 사용한 대부분의 반응에서 에너지 분포는 다양합니다.두 개 이상의 제품 세트가 발생할 수 있는 반응에 대해서는 분기 비율이 제공됩니다.

일부 반응 후보는 한 번에 탈락할 수 있습니다.D-Li⁶ 반응은 연소가 거의 어렵지만 D-D
²
₁
측면 반응을 통해 훨씬 더 많은 중성자를 생성하기 때문에 p-B에⁺¹¹
₅
비해 이점이 없다.p-Li⁺⁷
₃
반응도 있지만, T > 1 MeV일 경우를_i 제외하고 단면이 너무 낮지만, 그러한 고온에서는 흡열성 직접 중성자 생성 반응도 매우 중요해진다.마지막으로 p-Be⁺⁹
₄
반응도 있는데, 이것은 연소하기 어려울 뿐만
아니라 Be가 두 개의 알파 입자와 중성자로 쉽게 분열되도록 유도할 수 있다.

핵융합 반응 외에도, "건식" 핵융합 폭탄과 일부 제안된 핵융합 원자로에서 삼중수소를 "증식"하기 위해 중성자와 다음과 같은 반응이 중요하다.

n0	+	6 3리	→	3 1T .	+	4 2He + 4.784 MeV
n0	+	7 3리	→	3 1T .	+	4 2He + n0 - 2.467 MeV

두 공식 중 후자는 1954년 미국이 캐슬 브라보 핵융합실험을 했을 때 알려지지 않았다.Castle Bravo "Shrimp"의 설계자는 시험한 두 번째 핵융합 폭탄(그리고 리튬을 사용한 첫 번째)이기 때문에 삼중수소 생산에서 Li의 유용성을 이해했지만, Li 핵분열이 폭탄의 수율을 크게 증가시킬 것이라는 것을 인식하지 못했다.Li는 낮은 중성자 에너지를 위한 작은 중성자 단면을 가지고 있지만, 5 MeV 이상의 ^[33]단면을 가지고 있다.15 Mt의 수율은 예측된 6 Mt보다 250% 더 높았고 예상치 못한 낙진에 노출되었다.

이러한 반응의 유용성을 평가하려면 반응물, 제품 및 방출된 에너지 외에 핵 단면에 대해 알아야 한다.어떤 핵융합 장치라도 지속 가능한 최대 플라즈마 압력을 가지고 있으며 경제적인 장치는 항상 이 최대 압력에 가깝게 작동합니다.이 압력에 의해 온도가 δvµ²/T가 최대가 되도록 선택되었을 때 가장 큰 융접 출력을 얻을 수 있다.이는 점화 시 필요한 삼중곱 nTt의 값이 δv a/T에² 반비례하므로 최소가 되는 온도이기도 하다(로슨 기준 참조).(핵융합 반응이 외부 가열 없이 온도를 유지할 수 있는 충분한 전력을 생성하면 플라즈마는 "점화"된다.)이 최적 온도와 그 온도에서의 δvµ²/T 값은 다음 표의 몇 가지 반응에 대해 제시되어 있습니다.

연료	T [keV]	【v】/T23 [m/s2/keV]
2 1D -3 1T	13.6	1.24×10−24
2 1D -2 1D	15	1.28×10−26
2 1디헤 3 2	58	2.24×10−26
p+-6 3Li	66	1.46×10−27
p+-11 5B	123	3.01×10−27

반응의 대부분은 체인을 형성합니다.예를 들어 T와
He를 연료로 하는
원자로는 D를
만들어 에너지가 "적합"하면 D-He
³
₂
반응에 사용할 수 있다.(8)과 (9)의 반응을 조합하는 것이 우아한 아이디어입니다.반응(8)의 He는
완전히 열화되기 전에 반응(9)으로 Li와
반응할 수 있다.이것은 에너지 양성자를 생성하며, 양성자는 다시 열화되기 전에 반응(8)을 거친다.상세한 분석은 이 아이디어가 ^{[citation needed]}잘 작동하지 않을 것이라는 것을 보여주지만, 이것은 맥스웰 플라즈마의 일반적인 가정이 적절하지 않은 경우의 좋은 예이다.

중성자성, 제한 요건 및 전력 밀도

위의 반응들은 원칙적으로 핵융합 발전 생산의 기초가 될 수 있다.앞에서 설명한 온도와 단면 외에 융접제품_fus E의 총에너지, 하전융접제품_ch E의 에너지, 비수소반응물질의 원자번호 Z를 고려해야 한다.

그러나 D-D
²
₁
반응의 사양은 몇 가지 어려움을 수반한다.우선, 2개의 가지(2i)와 2ii에 걸쳐 평균을 내야 한다.더 어려운 것은 T와 He
제품을 어떻게
취급할지 결정하는 것입니다.³
₁T는
중수소 플라즈마에서 너무 잘 타서 플라즈마에서 추출하는 것이 거의 불가능하다.D-He
³
₂
반응은 훨씬 높은 온도에서 최적화되므로 최적의 D-D
²
₁
온도에서 연소율이 낮을 수 있습니다.따라서 T를
가정하는 것이 타당해 보이지만 He는
연소되어 순 반응에 에너지를 더한다. 즉, 총 반응은 (2i), (2ii) 및 (1)의 합이 된다.

5
D → He
+ 2 n⁰ + He
+ p⁺, E_fus = 4.03 + 17.6 + 3.27 = 24.9MeV, E_ch = 4.03+3.5+0.82 = 8.35 MeV.

원자로(는 반응률은 D-D 단계에 의해 결정된다)의 출력 계산 때문에, 우리는 Efus로=+(속 백만 일렉트론 볼트)×50%-=+D-D 반응이21D-21D 융합 에너지(4.03백만 전자 볼트 217.6백만 일렉트론 볼트)×50%12.5백만 일렉트론 볼트와 Ech 기소된 대로 입자들의 에너지(4.03백만 일렉트론 볼트+3.5백만 일렉트론 볼트)×50% 세(0.82 백만 일렉트론 볼트)×50%-4.2백만 전자 볼트.(주:삼중 수소 이온 반응.한 deuter여전히 큰 운동 에너지를 가지고 있는 동안, 생성된 헬륨-4의 운동 에너지는 3.5 ^[34]MeV와 상당히 다를 수 있습니다. 따라서 하전 입자의 에너지 계산은 평균의 근사치에 불과합니다.)중수소당 소비되는 에너지의 양은 이 중 2/5 또는 5.0 MeV(중수소 kg당 약 2억2500만 MJ의 특정 에너지)입니다.

D-D
²
₁
반응의 또 다른 독특한 측면은 반응속도를 계산할 때 고려해야 할 반응물이 하나뿐이라는 것이다.

이 선택을 통해 가장 중요한 4가지 반응에 대한 매개 변수를 표로 작성합니다.

절약형	Z	Efus [MeV]	Ech [MeV]
2 1D -3 1T	1	17.6	3.5	0.80
2 1D -2 1D	1	12.5	4.2	0.66
2 1디헤 3 2	2	18.3	18.3	00 0.05
p+-11 5B	5	8.7	8.7	0 0.001

마지막 열은 반응의 중성자, 중성자로 방출되는 핵융합 에너지의 비율입니다.이는 방사선 손상, 생물학적 차폐, 원격 취급 및 안전과 같은 중성자와 관련된 문제의 크기를 나타내는 중요한 지표이다.처음 두 반응의 경우 (E-E_fusch)/E로_fus 계산됩니다.이 계산으로 0을 얻을 수 있는 마지막 두 반응의 경우, 인용된 값은 열 평형 상태의 플라즈마에서 중성자를 생성하는 측면 반응에 기초한 대략적인 추정치이다.

물론 반응물질도 최적의 비율로 혼합해야 합니다.이것은 각 반응물 이온과 관련된 전자가 압력의 절반을 차지하는 경우입니다.즉, 총압력이 고정되어 있다고 가정할 때 비수소 이온의 입자 밀도가 수소 이온의 입자 밀도보다 2/(Z+1)계수만큼 작다는 것을 의미한다.따라서 이러한 반응의 속도는 δvrences/T² 값의 차이와 더불어 동일한 인자만큼 감소한다.반면 D-D
²
₁
반응은 반응물이 1개밖에 없기 때문에 연료가 두 개의 다른 수소 종으로 나뉘었을 때보다 속도가 두 배 높아 더 효율적인 반응을 만들어낸다.

따라서 핵융합 반응에 참여하지 않고 더 많은 전자를 필요로 하는 사실에서 발생하는 비수소 연료에 대한 "벌금"은 (2/(Z+1)이다.(일반적으로 전자 온도가 이온 온도와 거의 같다는 것은 좋은 가정입니다.그러나 일부 저자들은 전자가 이온보다 훨씬 더 차갑게 유지될 수 있다는 가능성에 대해 논의한다.이러한 경우, "핫이온 모드"로 알려진 "벌금"은 적용되지 않습니다.)동시에 D-D에
²
₁
대한 인자 2의 "보너스"가 있습니다. 왜냐하면 각 이온은 단지 일부만이 아니라 다른 이온들과 반응할 수 있기 때문입니다.

이제 다음 표에서 이러한 반응을 비교할 수 있습니다.

절약형	【v】/T2	/벌칙		로슨 기준	전력 밀도(W/m3/kPa2)	전력 밀도 역비
2 1D -3 1T	1.24×10−24	1	1	1	34	1
2 1D -2 1D	1.28×10−26	2	48	30	0.5	68
2 1디헤 3 2	2.24×10−26	2/3	83	16	0.43	80
p+-6 3Li	1.46×10−27	1/2	1700		0.005	6800
p+-11 5B	3.01×10−27	1/3	1240	500	0.014	2500

「v」/T² 의 최대치는, 상기의 테이블로부터 취득한 것입니다."벌금/보너스" 인자는 비수소 반응물 또는 단일 종 반응과 관련이 있습니다."역반응도" 열의 값은 1.24×10을⁻²⁴ 두 번째 열과 세 번째 열의 곱으로 나누어 구한다.이는 동등한 조건에서 다른 반응이 D-T
³
₁
반응보다 더 느리게 발생하는 요인을 나타낸다."로슨 기준" 열은 이러한 결과에 E로 가중치를_ch 부여하고 D-T
³
₁
반응의 난이도에 비해 이러한 반응으로 발화를 달성하는 것이 얼마나 더 어려운지를 나타낸다.다음에서 마지막 열에는 "전력 밀도"라는 레이블이 붙어 있으며 실제 반응성의 가중치는 E입니다_fus.마지막 열은 다른 반응의 핵융합 전력 밀도가 D-T
³
₁
반응에 비해 얼마나 낮은지 나타내며 경제적 잠재력의 척도로 간주할 수 있다.

준중성, 등방성 플라스마의 브렘스스트룽 손실

많은 시스템에서 핵융합 중인 이온은 기본적으로 단독으로 발생하는 것이 아니라 이온의 대량 전하를 중화시켜 플라즈마를 형성하는 전자와 혼합됩니다.전자는 일반적으로 이온과 비슷하거나 더 높은 온도를 가지기 때문에 이온과 충돌하여 10~30 keV 에너지의 X선 방사선을 방출합니다. 이 과정은 브렘스스트랄룽이라고 알려져 있습니다.

태양과 별의 거대한 크기는 이 과정에서 생성된 X선이 빠져나가지 않고 그들의 에너지를 플라스마로 다시 축적한다는 것을 의미한다.그것들은 엑스레이에 불투명하다고 알려져 있다.하지만 어떤 지상 핵융합로든 이 에너지 범위의 X선 때문에 광학적으로 얇아질 것이다.X선은 반사하기 어렵지만 (원자로 차폐의 일부인) mm 미만의 스테인리스강 두께에서 효과적으로 흡수(및 열로 변환)된다.즉, 브렘스스트룽 프로세스가 플라즈마로부터 에너지를 운반하여 냉각하는 것입니다.

벽에서 손실된 X선 방사선에 대한 핵융합 전력의 비율은 중요한 수치이다.이 비율은 일반적으로 전력 밀도를 최대화하는 온도보다 훨씬 높은 온도에서 최대화됩니다(앞의 항 참조).다음 표는 몇 가지 반응에 대한 최적 온도 및 해당 온도에서의 전력비의 추정치를 보여 줍니다.

연료	Ti(keV)	Pfusion/PBremsstrahlung
2 1D -3 1T	50	140
2 1D -2 1D	500	2.9
2 1디헤 3 2	100	5.3
3 2히히히 3 2	1000	0.72
p+-6 3Li	800	0.21
p+-11 5B	300	0.57

Bremsstrahlung 전력에 대한 실제 핵융합 비율은 몇 가지 이유로 상당히 낮을 수 있습니다.먼저, 이 계산은 핵융합 생성물의 에너지가 연료 이온으로 완전히 전달되고, 연료 이온은 충돌에 의해 전자에 에너지를 손실하고, 다시 브렘스스트라흐룽에 의해 에너지를 손실한다고 가정합니다.그러나 핵융합 생성물은 연료 이온보다 훨씬 더 빨리 움직이기 때문에 에너지의 상당 부분을 직접 전자에 전달하게 됩니다.둘째, 플라즈마 내의 이온은 순수 연료 이온으로 간주된다.실제로는 불순물 이온의 비율이 상당히 높기 때문에 그 비율이 낮아집니다.특히, 핵융합 생성물 자체는 에너지를 포기할 때까지 플라즈마 안에 있어야 하며, 제안된 감금 방식에서 한동안 남아 있어야 한다.마지막으로 브렘스스트라룽 이외의 모든 에너지 손실 경로는 무시되었습니다.마지막 두 요인은 관련이 있습니다.이론적이고 실험적인 근거에서 입자와 에너지의 제약은 밀접한 관련이 있는 것으로 보인다.에너지 보존이 잘 되는 가둬두기 방식에서는 핵융합 제품이 축적됩니다.핵융합 제품이 효율적으로 배출되면 에너지 제약도 약해집니다.

Bremsstrahlung에 비해 융접력을 최대화하는 온도는 모든 경우에 전력밀도를 최대화하고 융접 트리플 제품의 요구치를 최소화하는 온도보다 높습니다.이것은 Bremsstrahlung 비율이 낮기 때문에 D-T의
³
₁
최적 작동 지점을 크게 바꾸지는 않겠지만, 다른 연료는 D-T에
³
₁
대한 전력 밀도가 훨씬 낮고 필요한 제한을 달성하기가 더 어려운 시스템으로 밀어 넣을 것이다.D-D와
²
₁
D-He에
³
₂
있어서 Bremsstrahlung의 손실은 심각하고 아마도 엄청난 문제가 될 것이다.He-He
³
₂
, p-Li⁺⁶
₃
및 p-B의⁺¹¹
₅
경우, Bremsstrahlung 손실은 준중성, 등방성 플라즈마를 가진 이러한 연료를 사용하는 핵융합로를 불가능하게 만드는 것으로 보인다.이 딜레마에서 벗어날 수 있는 몇 가지 방법들이 고려되었지만 ^[35][36]거부되었다.이 제한은 비중립 플라스마 및 이방성 플라스마에는 적용되지 않지만 이러한 플라즈마에는 해결해야 할 과제가 있다.

단면의 수학적 설명

고전 물리학의 융합

고전적인 그림에서, 핵은 쿨롱 힘을 통해 서로를 밀어내지만 두 구가 접촉하기에 충분히 가까워지면 융합되는 단단한 구로 이해될 수 있다.원자핵의 반지름을 약 1펨토미터로 추정할 때, 두 수소의 융합에 필요한 에너지는 다음과 같다.

$({displaystyle E_{\ce {thresh}}=pic {1}{0}}{\frac {Z_{1}Z_{2}}{r}}{\ce {->[{\text {2 henator}}}}}}}{\frac {1}{\frac {4\pi \silonsylon_{0}}}}}} {frac} {\frac} {\frac} {\frac} {\frac} {{{}}} {\frac}}}$

$이$는 온도가 약 1.4 keV인 볼츠만 분포를 가진 태양의 $중심핵$의 경우 수소가 임계값에 도달할 ${\displaystyle {\mathrm{확률}}^{}}$은${\displaystyle {}^{}}$10$$- $290$ 즉 핵융합이 발생하지 않음을 의미합니다.그러나 태양에서의 융합은 양자역학으로 인해 일어난다.

단면 파라미터화

디브로글리 파장으로서의 유효 반지름의 스미싱과 전위장벽을 통한 양자 터널링 덕분에 융접이 일어날 확률은 고전 사진보다 크게 높아진다.핵융합 반응 속도를 결정하기 위해 가장 관심 있는 값은 상호작용의 특징적인 영역을 제공함으로써 입자가 융합할 확률을 설명하는 단면입니다.융접 단면적의 추정은 다음과 같이 세 부분으로 나뉩니다.

${\displaystyle \sigma \about \sigma _{geometry}\times T\times R}$

여기서 ${\displaystyle {\delta }_{}}$ g ${\displaystyle e_{}}$ ${\displaystyle o_{}}$ m ${\displaystyle e_{}}$ ${\displaystyle r_{}}$ y$$\ $displaystyle \sigma$_ { $geometry$}는$$ 기하학적 단면, T는 장벽 투명도, R은 반응의 반응 특성이다.

${\displaystyle {}_{}}$【 ${\displaystyle g_{}}$ ${\displaystyle e_{}}$ ${\displaystyle o_{}}$ ${\displaystyle m_{}}$ ${\displaystyle t_{}}$ ${\displaystyle r_{}}$$y$ 】 { $displaystyle$ \$$$displaystyle$ $_${ displaystyle$$ _ {${\displaystyle \frac{}{}{}^{}}$displaystyle _ { $displaystyle$ \ ${\displaystyle t_{}}$ r y${\displaystyle {}_{}}$} ${\displaystyle {h\mathrm{}}^{}}$ 2${\displaystyle {}^{}h\frac{\mathrm{}}{}}$ $1 、$ \ $displayda$^ { 2 }$= bigg$ ( \ $frac ）$ 。${\displaystyle m_{}}$ r$${ $display style$ m _ { $r$} $the$ $、$ \ $displaystyle$\ $silon }$는 시스템의 질량 에너지 중심입니다.

T는 Gamow 투과성으로 근사할 수 있습니다.투과도는 다음과 같습니다.${\displaystyle T}$ ${\displaystyle \approx {}^{}}$ - $g$${\displaystyle {\sqrt{{}_{}}}^{}}$G /$display$ { \ $displaystyle$T \ $approx$ e^ { - { \ $epsilon }$} ${\displaystyle （}$ ${\displaystyle z}$ ${\displaystyle {}_{}}$ ${\displaystyle {Z\mathrm{}}_{}}$ 1 ${\displaystyle {Z\mathrm{}}^{}{}_{}{}^{}{2\mathrm{}}_{}{}^{}}$） ${\displaystyle {}_{}}$ 2 × ${\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\displaystyle {r\mathrm{}}^{}}$2 ( \$displaystyle$\ ilon _ { G }$=$ ( \ $pi$ \ $alpha$ Z _ { 2 } )^{$2$} { 2 } } } } ^{ 2 }티알 장벽

R은 특정 반응의 모든 핵물리학을 포함하며 상호작용의 특성에 따라 매우 다른 값을 취합니다.그러나 대부분의 반응에서 R${\displaystyle }$( ${\displaystyle )}$) \ $displaystyle$ R ( \$epsilon$)의 변동은 Gamow factor 에서의 변동에 비해 작기 때문에 에너지가 약하게 변화하는 Astrophysical S-factor, $S{\displaystyle }$ ($$$)$ \ $displaystyle$S ( \epsilon $)$라고 하는 함수에 의해 근사된다.이러한 의존성을 종합하면, 에너지의 함수로서의 융접 단면에 대한 하나의 근사치가 다음과 같은 형태를 취합니다.

${\displaystyle \sigma (\epsilon )\약 {\epsilon }{-{\sqrt {\epsilon _ {G}/\epsilon }}}}$

단면의 보다 상세한 형태는 핵물리학 기반 모델과 R 매트릭스 이론을 통해 도출할 수 있다.

융접 단면의 공식

Naval Research Lab의 플라즈마 물리학^[37] 공식은 다음과 같은 공식에 의해 고정된 목표 이온에 대한 입사 입자의 에너지(keV)의 함수로 축사 단위의 총 단면을 제공합니다.

$1$$}$$NRL}}(\epsilon)=nfrac {A_{5}+{\big (}(A_{4}-A_{3}\epsilon)^2}+1(big)}{-1}A_{2}}{\epsilon(e^{})$$A_{1}\epsilon$^{-$1/2}}-1}}}$의 계수 값은 다음과 같습니다.

NRL 공식 단면 계수

	DT(1)	DD(2i)	DD(2ii)	DHe3(3)	TT(4)	THe3(6)
A1	45.95	46.097	47.88	89.27	38.39	123.1
A2	50200	372	482	25900	448	11250
A3	1.368×10−2	4.36×10−4	3.08×10−4	3.98×10−3	1.02×10−3	0
A4	1.076	1.22	1.177	1.297	2.09	0
답 5	409	0	0	647	0	0

또한^[38] Bosch-Hale은 R-행렬 계산 단면 적합 관측 데이터를 Padé 합리적 근사 계수와 함께 보고합니다.에너지는 keV 단위로, 단면은 밀리반 단위로, 인자는 다음과 같은 형태를 가진다.

$display S^$$\bigg}}{1+\epsilon(}B_{1}+\epsilon(}B_{2}+\epsilon (B_{3}+\epsilon B_{4}){\big$ 계수값:

융접 단면에 대한 Bosch-Hale 계수

	DT(1)	DD(2ii)	DHe3(3)	이4
${\displaystyle\epsilon_{G}}$	31.3970	68.7508	31.3970	34.3827
A1	5.5576×104	5.7501×106	5.1201×104	6.927×104
A2	2.1054×102	2.5226×103	3.3027×102	7.454×108
A3	- 3.2638×10−2	4.5566×101	- 1.2706×10−1	2.050×106
A4	1.4987×10−6	0	2.9327×10−5	5. 2002×104
답 5	1.8181×10−10	0	- 2.5151×10−9	0
지하 1층	0	-3.199×10−3	0	6.38×101
B2	0	- 8.5530×10−6	0	- 9.95×10−1
B3	0	5.9014×10−8	0	6.981×10−5
B4	0	0	0	1.728×10−4
적용 가능한 에너지 범위 [keV]	0.5-5000	0.3-900	0.5-4900	0.5-550
${\displaystyle(\Delta S)_{\text{max}}\%}$	2.0	2.2	2.5	1.9

여기서 ${\displaystyle \mathrm{bosch}}$ Bosch-Hale ${\displaystyle {}^{}}$ ${\displaystyle )}$ ) ${\displaystyle =}$ ${\displaystyle \frac{S}{}}$ ${\displaystyle \frac{{\text{Bosch-Hale}}^{}}{}}$(${\displaystyle \frac{}{g_{}}}$G /${\displaystyle \frac{ϵ\sqrt{}}{}}$) ${\displaystyle \frac{}{}}$ \ $display$ style$^$ { \$text$ { $Bosch$ - Hale } ( \ $epsilon$ ) =$frac$ { $S^$ { \$text${ $Bosch$ - Hale } ( \ epsilon ) \ epsilon \ expilon ) \ $scilon$）

맥스웰 평균 핵단면

열평형 상태에 있는 핵융합 시스템에서 입자는 Maxwell-Boltzmann 분포에 있습니다. 즉, 입자는 플라즈마 온도를 중심으로 에너지 범위를 가집니다.태양, 자기 구속 플라스마 및 관성 구속 융합 시스템은 열 평형 상태에 있도록 잘 모델링되어 있습니다.이 경우, 관심 값은 Maxwell-Boltzmann 분포에 걸쳐 평균화된 융접 단면이다.Naval Research Lab의 플라즈마 물리학 공식은 맥스웰의 평균 핵융합 단면 반응도를 c ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$/ ${\displaystyle \mathrm{s}}$ \ $displaystyle \mathrm {cm^{3}$ / $sec$ $단위$로 나타냅니다.

NRL 공식 핵융합 반응 속도는 맥스웰 분포에 대해 평균이었다.

온도 [keV]	DT(1)	DD(2ii)	DHe3(3)	TT(4)	(63)
1	5.5×10−21	1.5×10−22	1.0×10−26	3.3×10−22	1.0×10−28
2	2.6×10−19	5.4×10−21	1.4×10−23	7.1×10−21	1.0×10−25
5	1.3×10−17	1.8×10−19	6.7×10−21	1.4×10−19	2.1×10−22
10	1.1×10−16	1.2×10−18	2.3×10−19	7.2×10−19	1.2×10−20
20	4.2×10−16	5.2×10−18	3.8×10−18	2.5×10−18	2.6×10−19
50	8.7×10−16	2.1×10−17	5.4×10−17	8.7×10−18	5.3×10−18
100	8.5×10−16	4.5×10−17	1.6×10−16	1.9×10−17	2.7×10−17
200	6.3×10−16	8.8×10−17	2.4×10−16	4.2×10−17	9.2×10−17
500	3.7×10−16	1.8×10−16	2.3×10−16	8.4×10−17	2.9×10−16
1000	2.7×10−16	2.2×10−16	1.8×10−16	8.0×10−17	5.2×10−16

$에너지{\displaystyle }$ T${\displaystyle 25}$ 25 ${\displaystyle \text{keV}}${\$displaystyle$ T$\leq$ 25${\text{ keV}}}$의 경우 데이터는 다음과 같이 나타낼 수 있다.

${\displaystyle({\overline v}})_{DD}=2.33\times 10^{-14}\cdot T^{-2/3}\cdot e^{-18.76T^{-1/3}}{\text{cm}^{3}}/{\text{sec}}}}$

${\displaystyle({\overline v}})_{DT}=3.68\times 10^{-128\cdot T^{-2/3}\cdot e^{-19.94T^{-1/3}{\text{cm}}{3}}/{\text{sec}}$

KeV 단위로 T를 사용합니다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

• "What is Nuclear Fusion?". NuclearFiles.org. Archived from the original on 28 September 2006. Retrieved 12 January 2006.
• S. Atzeni; J. Meyer-ter-Vehn (2004). "Nuclear fusion reactions" (PDF). The Physics of Inertial Fusion. University of Oxford Press. ISBN 978-0-19-856264-1. Archived from the original (PDF) on 24 January 2005.
• G. Brumfiel (22 May 2006). "Chaos could keep fusion under control". Nature. doi:10.1038/news060522-2. S2CID 62598131.
• R.W. Bussard (9 November 2006). "Should Google Go Nuclear? Clean, Cheap, Nuclear Power". Google TechTalks. Archived from the original on 26 April 2007.
• A. Wenisch; R. Kromp; D. Reinberger (November 2007). "Science or Fiction: Is there a Future for Nuclear?" (PDF). Austrian Institute of Ecology.
• M. Kikuchi, K. Lackner & M. Q. Tran (2012). Fusion Physics. International Atomic Energy Agency. p. 22. ISBN 9789201304100.

외부 링크

• NuclearFiles.org – 원자력 관련 문서 저장소.
• 알소스 핵문제 디지털 라이브러리의 핵융합 관련 참고 문헌
• NRL Fusion 공식