핵구조

원자핵의 구조를 이해하는 것은 핵물리학에서 가장 중요한 과제 중 하나이다.

모델

액체 방울 모델

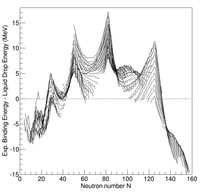
액체 방울 모델은 1935년 ^[1]칼 프리드리히 폰 바이제커에 의해 제안된 최초의 핵 구조 모델 중 하나이다.그것은 핵을 중성자와 양성자로 이루어진 반고전적인 유체로서, 양성자의 수에 비례하는 내부 반발 정전기력을 가지고 있다고 묘사한다.이들 입자의 양자역학적 특성은 파울리 배타원리를 통해 나타나는데, 파울리 배타원리는 같은 종류의 핵자 두 개가 같은 상태에 있을 수 없다는 것이다.그래서 그 유체는 사실 페르미 액체로 알려져 있다.이 모델에서 Z $(\displaystyle$ Z $)$ $N$ 와 $Z$ N $(\displaystyle$ N $)$ 중성자를 $N$ $가진$ 핵의 결합 에너지는 다음과 같이 주어진다.

E_{B}=a_{V}A-a_{S}A^{2/3}-a_{C}{\frac {Z^{2}}{A^{1/3}}-a_{A}{\frac {(N-Z)^{2}}{A}}-\delta(A,Z)

$A=Z+N$ 서 A $A=Z+N$ + $A=Z+N$ { $displaystyle$ A $=Z+$ $N}$ 은 $A=Z+N$ 총 핵자 수(질량 수)입니다. $A(\displaystyle$ A) 및 $A^{2/3}$ (\ $displaystyle$ A $^{2/3})$ 에 $A^{2/3}$ 비례하는 항은 액체 방울의 부피와 표면 에너지를 나타내고, $(\$ Z $^{2$ })에 $Z^{{2}}$ 비례하는 항은 정전기 에너지를 나타내고, ( $N$ - $)$ $(\$ display style Z)에 비례하는 항은^{2}}을 $(N-Z)^{2}$ $나타냅니다.$ 파울리 배타 원리와 마지막 항 $\delta (A,Z)$ ( $,$ Z $)$ ({ $displaystyle \delta$ ( $A,$ Z)})는 $\delta (A,Z)$ 짝수 양성자 또는 중성자에 대한 에너지를 낮추는 쌍체 용어이다. $a_{V},a_{S},a_{C},a_{A}$ $a_{V},a_{S},a_{C},a_{A}$ $a_{V},a_{S},a_{C},a_{A}$ $({$ $a_{V},a_{S},a_{C},a_{A}$ 및 쌍화 항의 강도는 이론적으로 추정하거나 데이터에 적합할 수 있습니다.이 단순한 모델은 핵의 결합 에너지의 주요 특징을 재현합니다.

페르미 액체의 방울로서의 핵의 가정은 미지의 ^[2]핵의 예측에 필요한 정확도와 함께 전체 차트에서 핵 결합 에너지가 잘 재생될 수 있기 때문에 FRDM(Finite Range Droplet Model)의 형태로 여전히 널리 사용되고 있다.

셸 모델

쉘 모델이라는 표현은 최첨단 두 개의 다른 시대를 지칭한다는 점에서 모호하다.그것은 이전에 현재 평균장 이론이라고 불리는 것에 더 가까운 접근법에 따라 핵에서 핵자 껍데기의 존재를 설명하는 데 사용되었습니다.오늘날, 그것은 양자 화학에서 사용되는 구성 상호작용 형식주의와 유사한 형식주의를 말한다.여기서 후자를 소개하겠습니다.

셸 개념 소개

Z>7에 대한 중성자 수 함수로서의 실험 결합 에너지와 액적 모델 예측의 차이

원자핵의 결합에너지의 체계적인 측정은 액체 방울 모델에서 추정된 것과 관련하여 체계적인 편차를 보여준다.특히 양성자 및/또는 중성자 수에 대해 특정 값을 가진 일부 핵은 액적 모델에 의해 예측된 것보다 더 단단하게 결합되어 있다.이러한 핵을 단일/이중 마법이라고 합니다.이러한 관찰은 과학자들이 원자 안에 있는 전자와 같이 핵 안에 있는 핵자 (원자와 중성자)의 껍데기 구조의 존재를 가정하도록 이끌었다.

사실, 핵자는 양자 물체이다.엄밀히 말하면, 각각의 핵자는 서로 상관관계가 있기 때문에, 각각의 핵자의 에너지에 대해 이야기해서는 안 된다.그러나 근사치로서 핵자가 개별적으로 번식하는 평균 핵을 상상할 수 있다.양자 특성으로 인해, 그들은 분리된 에너지 수준만을 차지할 수 있다.이러한 레벨은 결코 균일하게 분포되어 있지 않습니다.에너지 간격은 혼잡하고 일부는 비어 있어 가능한 에너지의 갭을 생성합니다.셸은 넓은 빈 틈으로 다른 레벨과 분리된 레벨의 집합입니다.

에너지 수준은 단일 핵자가 다른 모든 핵자에 의해 생성된 평균 전위 안에서 움직이는 슈뢰딩거 방정식을 풀면 알 수 있습니다.각 레벨은 핵자에 의해 점유되거나 비워질 수 있습니다.어떤 레벨은 같은 에너지를 가진 여러 다른 양자 상태를 수용한다; 그것들은 퇴화되었다고 한다.이것은 특히 평균 핵이 어느 정도 대칭을 가지고 있는 경우에 발생합니다.

껍데기의 개념은 왜 어떤 핵들이 다른 핵들보다 더 단단하게 묶여있는지 이해할 수 있게 해준다.이는 같은 종류의 두 핵자가 같은 상태에 있을 수 없기 때문이다(Pauli 제외 원리).그래서 핵의 가장 낮은 에너지 상태는 핵자가 모든 에너지 레벨을 바닥에서 일정 수준까지 채우는 것입니다.완전한 껍데기를 가진 핵은 설명될 것처럼 매우 안정적입니다.

전자껍질 모델의 전자와 마찬가지로, 가장 바깥쪽 껍질의 양성자는 핵의 중심에서 가장 멀리 떨어져 있기 때문에, 그 껍질에 양성자가 거의 없다면 상대적으로 느슨하게 핵에 결합되어 있습니다.따라서, 완전한 외부 양성자 껍데기를 가진 핵은 유사한 총 양성자 수를 가진 다른 핵들보다 더 단단하게 결합되고 더 높은 결합 에너지를 가질 것이다.이것은 중성자에도 해당된다.

또한, 핵을 자극하는 데 필요한 에너지(즉, 이전에 점유되지 않은 더 높은 수준으로 핵자를 이동시키는 것)는 그러한 핵에서 예외적으로 높다.이 비어있는 수준이 완전한 껍데기 다음 단계일 때, 핵을 자극하는 유일한 방법은 틈새를 가로질러 하나의 핵자를 일으켜서 많은 에너지를 소비하는 것입니다.그렇지 않으면, 가장 높은 점유 에너지 레벨이 부분적으로 채워진 껍질에 있다면, 같은 껍질에서 핵자를 더 높은 상태로 올리는 데 훨씬 적은 에너지가 필요합니다.

안정적인 핵에서 관찰된 셸 구조의 진화는 안정성의 계곡에서 멀어질 것으로 예상된다.예를 들어 불안정한 동위원소 관측 결과 셸 구조가 구성된 ^[3]단일 입자 레벨의 이동 및 정렬이 나타났습니다.이것은 때때로 반전의 섬이 생기거나 전통적인 매직 수치보다 높은 들뜸 에너지 갭의 감소로 관찰된다.

기본 가설

셸 모델에 정확한 개념 프레임워크를 제공하기 위해 다음과 같은 기본적인 가설이 제시됩니다.

원자핵은 양자 N-체계이다.
핵 내의 핵자의 내부 운동은 상대적이지 않으며, 그들의 행동은 슈뢰딩거 방정식에 의해 지배된다.
핵자는 내부 구조가 없는 점 같은 것으로 간주됩니다.

형식주의에 대한 간략한 설명

셸 모델 계산에 사용되는 일반적인 프로세스는 다음과 같습니다.먼저 핵에 대한 해밀턴이 정의된다.일반적으로 계산의 실용성을 위해 이 정의에서는 일체 항과 이체 항만 고려된다.교호작용은 실험 데이터와 함께 적합되어야 하는 자유 모수를 포함하는 효과적인 이론입니다.

다음 단계는 단일 입자 상태의 기초, 즉 모든 가능한 핵자 상태를 설명하는 일련의 파동 함수를 정의하는 것으로 구성된다.대부분의 경우, 이 근거는 Hartree를 통해 얻습니다.포크 계산이러한 단일 입자 상태의 집합에서 슬레이터 결정 인자는 단일 입자 파동 함수의 반대칭 산물인 Z 양성자 변수 또는 N 중성자 변수에 대한 파동 함수(핵자 쌍에 대한 변수 교환 시 파동 함수는 신호만 변화한다는 의미)를 구축한다.

원칙적으로, 유한 에너지에서 단일 핵자가 사용할 수 있는 양자 상태의 수는 유한하다(예를 들어 n).핵에 있는 핵자의 수는 사용 가능한 상태의 수보다 작아야 하며, 그렇지 않으면 핵이 모든 핵자를 보유할 수 없습니다.따라서 n개의 가능한 상태 중에서 Z(또는 N) 상태를 선택하는 방법은 여러 가지가 있습니다.조합 수학에서, n개의 Z 객체의 선택 횟수는 이항 계수^Z
_n C이다.n이 Z(또는 N)보다 훨씬 크면 이 값은 대략 n과 같이^Z 증가합니다.실제로 이 숫자는 8보다 큰 A=N+Z에 대해서는 모든 계산이 불가능할 정도로 커진다.

이러한 어려움을 피하기 위해, 가능한 단일 입자 상태의 공간은 화학과 유추에 의해 코어 및 원자가 전자로 나뉩니다(핵심 전자 및 원자가 전자 참조).노심은 단일 입자의 집합이며, 이러한 입자는 잘 결합되는 최저 에너지 상태이며 그 상황을 재점검할 필요가 없다는 점에서 비활동적이라고 가정한다.코어에는 없는 모든 단일 입자 상태의 공간인 원자가 공간의 상태와 달리 슬레이터 결정 요소에는 나타나지 않지만, (Z-) N-체 파동 기능의 구축 선택에서 고려될 수 있다.원자가 공간에서 가능한 모든 슬레이터 결정 인자의 세트는 (Z-) N-body 상태의 기초를 정의합니다.

마지막 단계는 이 기준 내에서 해밀턴 행렬을 계산하고 그것을 대각화하는 것이다.코어의 고정에 의해 베이스의 치수가 감소해도 대각화되는 행렬은 10차원의⁹ 치수에 쉽게 도달해 특정 대각화 기술을 요구한다.

셸 모형 계산은 일반적으로 실험 데이터에 매우 적합합니다.그러나 이러한 요소는 두 가지 주요 요인에 크게 좌우됩니다.

단일 입자 공간을 코어 및 원자가로 나누는 방법.
효과적인 핵자-핵자 상호작용.

평균 필드 이론

독립 입자 모델(IPM)

강한 상호작용의 결과이고 핵 내에서 핵자를 결합하는 핵자 사이의 상호작용은 유한한 범위를 갖는 독특한 행동을 보인다: 두 핵자 사이의 거리가 너무 커지면 사라진다; 중간 범위에서는 매력적이고 매우 작은 범위에서는 혐오스럽다.이 마지막 특성은 두 개의 페르미온(핵자는 페르미온)이 같은 양자 상태에 있을 수 없다는 파울리 배제 원리와 관련이 있다.그 결과 ^[4]핵 내의 핵자에 대해 예측된 매우 큰 평균 자유 경로가 발생한다.

독립 입자 접근법의 주요 개념은 핵자가 다른 핵자와 독립적으로 특정 잠재적 우물 안에서 움직이는 것입니다.이는 N-body 문제(N개의 입자가 상호작용)를 N개의 단체 문제로 대체하는 것입니다.이 문제의 본질적인 단순화는 평균 필드 이론의 초석이다.이것들은 또한 중심핵과 전자 구름 그 자체 때문에 전자가 평균장에서 움직이는 원자 물리학에서도 널리 사용된다.

독립입자모델과 평균장론(여러 가지 변형이 존재하는 것을 알 수 있다)은 유효상호작용 또는 유효전위로부터 시작하는 핵의 특성을 기술하는 데 큰 성공을 거두어 원자핵론의 기초가 된다.또한 모델을 확장하여 핵 쌍이나 회전과 같은 핵자의 집합 운동이나 진동과 같은 효과를 도입하는 것이 매우 쉽기 때문에 형식주의에서 대응하는 에너지 용어를 추가하는 것이 충분히 모듈화되어 있다는 점도 주목해야 한다.이는 많은 표현에서 평균장이 집단 들뜸 및 핵자 ^[5]^[6]이동과 같은 특성을 재현하는 상관관계를 도입하는 보다 완전한 설명을 위한 시작점일 뿐이라는 것을 의미한다.

핵잠재력과 효과적인 상호작용

평균장 이론에서 직면한 실제 어려움의 큰 부분은 평균장 자체의 잠재력의 정의(또는 계산)이다.다음 두 가지 접근방식을 대강 구별할 수 있습니다.

현상학적 접근방식은 적절한 수학적 함수에 의한 핵잠재력의 매개 변수화이다.역사적으로, 이 절차는 잠재적인 (변형된) 고조파 발진기 전위로 사용된 Sven Gösta Nilsson에 의해 가장 큰 성공을 거두었다.예를 들어, 가장 최근의 매개변수화는 산란 실험을 더 정확하게 설명하는 보다 현실적인 함수를 기반으로 합니다.특히 우즈 색슨 잠재력이라고 알려진 형태를 언급할 수 있다.
자기 정합성이 강한 사람 또는 하트리-Fock 접근방식은 효과적인 핵자-핵자 상호작용에서 핵잠재력을 수학적으로 추론하는 것을 목표로 한다.전위는 결정되는 파동 함수에 따라 달라지기 때문에 이 기술은 반복적인 방식으로 슈뢰딩거 방정식의 분해능을 의미한다.후자는 슬레이터 행렬식으로 작성됩니다.

하트리호의 경우-Fock이 접근하면 문제는 핵잠재력을 가장 잘 설명하는 수학적 함수를 찾는 것이 아니라 핵자-핵자 상호작용을 가장 잘 설명하는 함수를 찾는 것이다.실제로, 상호작용이 알려진 원자물리학과는 대조적으로(쿨롱 상호작용이다), 핵 내의 핵자-핵자 상호작용은 분석적으로 알려져 있지 않다.

이 사실에는 크게 두 가지 이유가 있다.첫째, 강한 상호작용은 핵자를 형성하는 쿼크 사이에서 본질적으로 작용합니다.진공에서의 핵자-핵자 상호작용은 쿼크-쿼크 상호작용의 결과일 뿐이다.후자는 높은 에너지에서 표준 모델의 프레임워크에서 잘 이해되지만, 색 제한과 점근 자유로 인해 낮은 에너지에서는 훨씬 더 복잡하다.따라서 쿼크-쿼크 상호작용으로부터 핵-핵자 상호작용을 추론할 수 있는 기본 이론은 아직 없다.게다가 이 문제가 해결되더라도 진공상태에서 상호작용하는 두 개의 핵자와 핵물질에서 상호작용하는 이들 핵자 사이에는 여전히 큰 차이가 있을 것이다.더 나아가기 위해서는 효과적인 상호작용의 개념을 고안할 필요가 있었다.후자는 기본적으로 실험 데이터와 일치하도록 조정되는 몇 가지 임의 매개변수를 가진 수학 함수입니다.

대부분의 현대 상호작용은 제로 레인지이기 때문에 토니 스카이라메가 ^[7]소개한 것처럼 두 핵자가 접촉할 때만 작용합니다.

하트리족의 자기일관적 접근법-폭 타입

하트리에서는...n-물체 문제의 Fock 접근법, 시작점은 n개의 운동 에너지 항과 전위 항을 포함하는 해밀턴이다.앞서 언급했듯이, 평균장 이론 가설 중 하나는 이체 상호작용만 고려되어야 한다는 것이다.해밀턴의 전위항은 n개의 페르미온 집합에서 가능한 모든 2체 상호작용을 나타낸다.그것은 첫 번째 가설이다.

두 번째 단계는 시스템의 파동 함수가 1입자 스핀-오비탈의 슬레이터 결정식으로 기록될 수 있다고 가정하는 것으로 구성됩니다.이 문장은 독립 입자 모델의 수학적 번역입니다.이것이 두 번째 가설입니다.

이 슬레이터 결정요인의 성분, 즉 핵자의 개별 파동 함수를 결정하는 것은 이제 남아 있다.이를 위해 전체 파동 함수(슬레이터 결정식)는 에너지가 최소가 되도록 가정한다.이것이 세 번째 가설입니다.

엄밀히 말하면, (알려지지 않은) 슬레이터 행렬식에서 (알려진) 2체 해밀턴의 평균값을 계산해야 하고, 그 수학적 변화가 사라지도록 강요해야 한다는 것을 의미한다.이는 미지수가 개별 파동함수인 하트리 방정식으로 이어진다.Fock 방정식.이러한 방정식을 푸는 것은 핵자의 파동함수와 개별 에너지 수준, 그리고 따라서 핵과 그 파동함수의 총 에너지를 제공합니다.

하트리족에 대한 짧은 설명-Fock 방법은 왜 그것이 변이적 접근법이라고도 불리는지를 설명한다.계산을 시작할 때, 총 에너지는 "개별 파동 함수의 함수"(이른바 함수)이며, 모든 것은 이러한 파동 함수의 선택을 최적화하기 위해 만들어지며, 그 함수가 국소적인 것이 아니라 최소한의 절대적인 것이 되도록 한다.좀 더 정확하게 말하면, 에너지는 밀도의 함수이며, 개별 제곱 파동 함수의 합으로 정의된다는 것을 언급해야 한다.더 하트리-Fock 방법은 또한 밀도 함수 이론(DFT)으로 원자 물리학과 응축 물질 물리학에서도 사용됩니다.

하트리 문제를 해결하는 과정-포크 방정식은 반복적일 수 밖에 없는데, 이는 사실 전위가 밀도에 따라 달라지는 슈뢰딩거 방정식이기 때문입니다. 즉, 정확히 결정되는 파동 함수에 따라 달라지기 때문입니다.실질적으로 알고리즘은 개개의 총합적으로 합리적인 파동함수(일반적으로 고조파 발진기의 고유함수) 세트로 시작됩니다.이것들은 밀도를 계산할 수 있게 하고, 거기서 하트리로부터-Fock 잠재력.이렇게 하면 슈뢰딩거 방정식이 다시 풀립니다.연이은 2회 반복의 파동함수 또는 에너지 레벨의 차이가 고정값보다 작을 경우 계산이 중지됩니다.그러면 평균 전위가 완전히 결정되고, 하트리-폭 방정식은 표준 슈뢰딩거 방정식이 됩니다.대응하는 해밀턴을 하트리라고 한다.폭스 해밀턴.

상대론적 평균장이 접근합니다.

1970년대에 양자강체역학에 대한 존 더크 왈레카의 연구로 처음 태어난 핵의 상대론적 모델은 1980년대 말에 P에 의해 날카로워졌다.반지와 동료들.이러한 접근법의 출발점은 상대론적 양자장 이론이다.이 맥락에서, 핵자 상호작용은 중간자라고 불리는 가상 입자의 교환을 통해 일어납니다.첫 번째 단계에서는 이러한 상호작용 항을 포함하는 라그랑지안을 만드는 것입니다.둘째, 최소 작용 원리를 적용함으로써 일련의 운동 방정식을 얻을 수 있다.실제 입자(여기서는 핵자)는 디락 방정식을 따르는 반면, 가상 입자(여기서는 중간자)는 클라인-고든 방정식을 따릅니다.

강한 상호작용의 비격동적 특성 및 핵자 그룹 간의 상호작용의 정확한 잠재적 형태가 상대적으로 잘 알려져 있지 않다는 점에서 원자핵의 경우 그러한 접근방식의 사용은 급격한 근사치를 필요로 한다.주요 단순화는 방정식의 모든 필드 항(수학적 의미에서의 연산자)을 평균 값(함수)으로 대체하는 것입니다.이러한 방법으로, 사람들은 결합된 적분-미분 방정식의 시스템을 얻게 되는데, 이것은 분석적이 아니더라도 수치적으로 풀 수 있다.

상호작용 보손 모형

상호작용 보손 모델(IBM)은 핵자가 0, 2 또는 4의 적분 스핀으로 각각 보손 입자로 작용하는 쌍으로 표현되는 핵물리학 모델이다.이것은 더 큰 핵에 대한 계산을 가능하게 한다.이 모델에는 여러 가지가 있다. 그 중 한 가지(IBM-1)에서는 모든 유형의 핵자를 쌍으로 그룹화할 수 있고, 다른 것(예: IBM-2)에서는 양성자와 중성자를 쌍으로 따로 고려할 수 있다.

핵물리학의 대칭성 자연파괴

모든 물리학의 초점 중 하나는 대칭이다.핵자-핵자 상호작용과 실제로 사용되는 모든 유효 상호작용은 특정한 대칭을 가진다.변환(방향이 변경되지 않도록 기준 프레임을 변경), 회전(기준 프레임을 일부 축 중심으로 회전) 또는 패리티(축의 감각 변경)에 의해 이러한 작업 중 어느 것도 상호 작용이 변경되지 않는다는 의미에서 변하지 않습니다.그럼에도 불구하고, 하트리에서는-Fock 접근법, 그러한 대칭에서 불변하지 않는 솔루션이 나타날 수 있습니다.누군가는 자발적인 대칭이 깨지는 것에 대해 말한다.

질적으로, 이러한 자발적인 대칭 깨짐은 다음과 같은 방법으로 설명될 수 있습니다: 평균 장 이론에서, 핵은 독립적인 입자의 집합으로 설명됩니다.평균 필드에 들어가지 않는 핵자 사이의 대부분의 추가 상관관계는 무시된다.그러나 그것들은 평균장 해밀턴의 대칭이 깨지면 나타날 수 있는데, 이는 단지 근사치이다.밀도가 하트리 반복을 시작하는 데 사용된 경우-Fock 프로세스는 특정 대칭을 깨며, 최종 Hartree-Fock Hamiltonian은 총 에너지의 관점에서 이러한 대칭을 깨는 것이 유리하다면 이러한 대칭을 깨트릴 수 있습니다.

또한 대칭 해를 향해 수렴할 수도 있습니다.어떤 경우에도 최종 솔루션이 대칭, 예를 들어 회전 대칭을 깨서 핵이 구형이 아닌 타원형으로 보인다면, 회전에 의해 변형된 핵에서 추론된 모든 구성은 하트리에게 좋은 해결책이다.포크의 문제그러면 핵의 접지 상태가 퇴화됩니다.

핵 쌍에서도 유사한 현상이 발생하며 이는 중입자 수 보존에 위배된다(아래 참조).

평균장 이론의 확장

핵쌍성 현상

평균 장 이론의 가장 일반적인 확장은 핵 쌍성이다.짝수 핵자를 가진 핵자는 홀수 핵자보다 체계적으로 더 많이 결합되어 있다.이는 각 핵자가 서로 결합해 쌍을 형성한다는 것을 의미하며, 결과적으로 시스템은 공통 평균장을 받는 독립 입자로 기술될 수 없다.핵에 짝수 수의 양성자와 중성자가 있을 때 각각 짝을 찾습니다.이러한 시스템을 활성화하려면 적어도 한 쌍을 깨트릴 정도의 에너지를 사용해야 한다.반대로, 홀수 수의 양성자나 중성자의 경우, 들뜨는 데 더 적은 에너지가 필요한 짝이 없는 핵자가 존재한다.

이 현상은 고체물리학의 제1종 초전도 현상과 매우 유사하다.핵 쌍성의 첫 번째 이론적 설명은 1950년대 말에 Aage Bohr, Ben Motelson,^[8] 그리고 David Pines에 의해 제안되었다.이는 금속 초전도 현상을 설명하는 바딘, 쿠퍼, 슈리퍼의 BCS 이론에 가까웠다.이론적으로, BCS 이론에 의해 기술된 쌍화 현상은 평균장 이론과 결합된다: 핵자는 평균장 전위와 쌍화 상호작용의 대상이다.

더 하트리-Fock-Bogolyubov(HFB) 방법은 보다 정교한 접근법으로, 동등한 기반에서 쌍성과 평균 필드 상호작용을 일관되게 고려할 수 있다.HFB는 현재 핵 시스템의 평균 현장 처리에서 사실상의 표준이다.

대칭 복원

평균 필드 방법의 특이성은 명시적 대칭 파괴에 의한 핵 특성 계산이다.자가 일관성 있는 방법(예: Hartree-Fock)을 사용하여 평균 필드를 계산하면 회전 대칭이 깨지고 짝짓기 특성이 계산되면 입자 번호가 깨집니다.

좋은 양자수를 투영하여 대칭을 회복하기 위한 몇 가지 기술이 ^[10]개발되었습니다.

입자 진동 커플링

평균 필드 방법(결국 대칭 복원을 고려)은 독립 입자 시스템을 가정하는 경우에도 시스템의 접지 상태에 대한 좋은 근사치이다.고차 보정은 입자들이 상관 관계를 통해 서로 상호작용한다는 사실을 고려합니다.이러한 상관관계는 독립적인 입자 자유도, 짝수 수의 양성자와 중성자를 가진 시스템의 저에너지 집단 들뜸의 결합을 고려해 도입할 수 있다.

이와 같이 들뜬 상태는 무작위 위상 근사(RPA)를 통해 재현될 수 있으며, 최종적으로는 지면 상태에 대한 보정도 일관되게 계산할 수 있다(예: 핵장^[6] 이론).

「」를 참조해 주세요.

핵자기 모멘트
CARISA, 핵구조 연구 콜라보레이션

추가 정보

일반 사용자

제임스 M.Cork ; Radio Activité & Physical nucleaire, Dunod (1949)

도입부 텍스트

Luc Valentin; Le monde subatomique - Des Quarks aux centrales nucleaires, 헤르만(1986)
Luc Valentin; Noyaux et partules - Modéles et symétries, Hermann (1997).
David Halliday ;핵물리학 입문, Wiley & Sons (1957).
Kenneth Krane; Wiley & Sons(1987년).
Carlos Bertulani; Nuclear Physics in a Nutshell, Princeton University Press (2007).

기본 텍스트

피터 E. 호지슨: 핵반응과 핵구조.옥스퍼드 대학 출판부(1971년).
Irving Kaplan; 핵물리학, 핵과학 및 엔지니어링의 애디슨-웨슬리 시리즈, 애디슨-웨슬리(1956)제2판 (제2판)
A. Bohr & B.모텔슨; 핵구조, 2권, 벤자민(1969년-1975년).제1권 : 단입자 운동; 제2권 : 핵변형.Rédité par World Scientific Publishing Company(1998), ISBN 981-02-3197-0.
P. Ring & P. Schuck;핵 다체 문제, Springer Verlag(1980), ISBN 3-540-21206-X
A. de Shalit & H. Feshbach; 이론핵물리학, 2권, John Wiley & Sons(1974).제1권 : 핵구조, 제2권 : 핵반응, ISBN 0-471-20385-8

레퍼런스

^ von Weizsäcker, C. F. (1935). "Zur Theorie der Kernmassen". Zeitschrift für Physik (in German). 96 (7–8): 431–458. Bibcode:1935ZPhy...96..431W. doi:10.1007/BF01337700. S2CID 118231854.
^ Moeller, P.; Myers, W. D.; Swiatecki, W. J.; Treiner, J. (3 Sep 1984). "Finite Range Droplet Model". Conference: 7. International Conference on Atomic Masses and Fundamental Constants (AMCO-7), Darmstadt-Seeheim, F.R. Germany. OSTI 6441187.
^ Sorlin, O.; Porquet, M.-G. (2008). "Nuclear magic numbers: New features far from stability". Progress in Particle and Nuclear Physics. 61 (2): 602–673. arXiv:0805.2561. Bibcode:2008PrPNP..61..602S. doi:10.1016/j.ppnp.2008.05.001. S2CID 118524326.
^ Brink, David; Broglia, Ricardo A. (2005). Nuclear Superfluidity. Cambridge University Press. ISBN 9781139443074.
^ Ring, P.; Schuck, P. (1980). The nuclear many-body problem. Springer Verlag. ISBN 978-3-540-21206-5.
^ ^a ^b Idini, A.; Potel, G.; Barranco, F.; Vigezzi, E.; Broglia, R. A. (2015). "Interweaving of elementary modes of excitation in superfluid nuclei through particle-vibration coupling: Quantitative account of the variety of nuclear structure observables". Physical Review C. 92 (3): 031304. arXiv:1504.05335. Bibcode:2015PhRvC..92c1304I. doi:10.1103/PhysRevC.92.031304. S2CID 56380507.
^ Beiner, M.; Flocard, H.; Van Giai, Nguyen; Quentin, P. (1975). "Nuclear ground-state properties and self-consistent calculations with the skyrme interaction". Nuclear Physics A. 238: 29–69. Bibcode:1975NuPhA.238...29B. doi:10.1016/0375-9474(75)90338-3.
^ Broglia, Ricardo A.; Zelevinsky, Vladimir (2013). Fifty Years of Nuclear BCS: Pairing in Finite Systems. World Scientific. doi:10.1142/8526. ISBN 978-981-4412-48-3.
^ "Hartree-Fock-Bogoliubov Method".
^ Bayman, B. F. (1960). "A derivation of the pairing-correlation method". Nucl. Phys. 15: 33–38. Bibcode:1960NucPh..15...33B. doi:10.1016/0029-5582(60)90279-0.

외부 링크

영어

(영어) 프랑스 IPN(Institut de Feechys Nucleaire)
(영어) 독일 안티프로톤 이온 연구 시설(FAIR)
(영어) 독일 GSI(Gesellschaft für Schwerionenforschung)
(영어) 러시아 원자력 공동 연구소
(영어) Argonne 국립연구소(ANL), 미국
(영어) 리켄(일본)
(영어) 미국 미시간 주립 대학교 국립 초전도 사이클로트론 연구소
(영어) 미국 미시간 주립 대학교 희귀 동위원소 빔 시설

프랑스어

(프랑스어) 프랑스 IPN(Institut de Feechys Nucleaire)
(프랑스어) Centre de Spectrométrie Nucleaire et de Spectrométrie de Mass(프랑스 CSNSM)
(프랑스어) Service de Physience Nucleaire CEA/DAM(프랑스)
(프랑스어) 국립 체격 연구소 (프랑스, Nucle Nucleaire et de Feechite des Particules (프랑스)
(프랑스어) 그랜드 악셀레라튀르 내셔널 디옹 루드(GANIL), 프랑스
(프랑스어) 프랑스 에너지 아토미크 위원회
(프랑스어) 스위스의 유로펜 드 레체르쉬 센터 누클레어즈
핵종의 LiveChart - IAEA

[1] von Weizsäcker, C. F. (1935). "Zur Theorie der Kernmassen". Zeitschrift für Physik (in German). 96 (7–8): 431–458. Bibcode:1935ZPhy...96..431W. doi:10.1007/BF01337700. S2CID 118231854.

[2] Moeller, P.; Myers, W. D.; Swiatecki, W. J.; Treiner, J. (3 Sep 1984). "Finite Range Droplet Model". Conference: 7. International Conference on Atomic Masses and Fundamental Constants (AMCO-7), Darmstadt-Seeheim, F.R. Germany. OSTI 6441187.

[3] Sorlin, O.; Porquet, M.-G. (2008). "Nuclear magic numbers: New features far from stability". Progress in Particle and Nuclear Physics. 61 (2): 602–673. arXiv:0805.2561. Bibcode:2008PrPNP..61..602S. doi:10.1016/j.ppnp.2008.05.001. S2CID 118524326.

[4] Brink, David; Broglia, Ricardo A. (2005). Nuclear Superfluidity. Cambridge University Press. ISBN 9781139443074.

[5] Ring, P.; Schuck, P. (1980). The nuclear many-body problem. Springer Verlag. ISBN 978-3-540-21206-5.

[NFT-6] Idini, A.; Potel, G.; Barranco, F.; Vigezzi, E.; Broglia, R. A. (2015). "Interweaving of elementary modes of excitation in superfluid nuclei through particle-vibration coupling: Quantitative account of the variety of nuclear structure observables". Physical Review C. 92 (3): 031304. arXiv:1504.05335. Bibcode:2015PhRvC..92c1304I. doi:10.1103/PhysRevC.92.031304. S2CID 56380507.

[7] Beiner, M.; Flocard, H.; Van Giai, Nguyen; Quentin, P. (1975). "Nuclear ground-state properties and self-consistent calculations with the skyrme interaction". Nuclear Physics A. 238: 29–69. Bibcode:1975NuPhA.238...29B. doi:10.1016/0375-9474(75)90338-3.

[8] Broglia, Ricardo A.; Zelevinsky, Vladimir (2013). Fifty Years of Nuclear BCS: Pairing in Finite Systems. World Scientific. doi:10.1142/8526. ISBN 978-981-4412-48-3.

[9] "Hartree-Fock-Bogoliubov Method".

[10] Bayman, B. F. (1960). "A derivation of the pairing-correlation method". Nucl. Phys. 15: 33–38. Bibcode:1960NucPh..15...33B. doi:10.1016/0029-5582(60)90279-0.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

Search

핵구조

네임스페이스

더

목차

모델

액체 방울 모델

셸 모델

셸 개념 소개

기본 가설

형식주의에 대한 간략한 설명

평균 필드 이론

독립 입자 모델(IPM)

핵잠재력과 효과적인 상호작용

하트리족의 자기일관적 접근법-폭 타입

상대론적 평균장이 접근합니다.

상호작용 보손 모형

핵물리학의 대칭성 자연파괴

평균장 이론의 확장

핵쌍성 현상

대칭 복원

입자 진동 커플링

「」를 참조해 주세요.

추가 정보

일반 사용자

도입부 텍스트

기본 텍스트

레퍼런스

외부 링크

Search

핵구조

모델

액체 방울 모델

셸 모델

셸 개념 소개

기본 가설

형식주의에 대한 간략한 설명

평균 필드 이론

독립 입자 모델(IPM)

핵잠재력과 효과적인 상호작용

하트리족의 자기일관적 접근법-폭 타입

상대론적 평균장이 접근합니다.

상호작용 보손 모형

핵물리학의 대칭성 자연파괴

평균장 이론의 확장

핵쌍성 현상

대칭 복원

입자 진동 커플링

「 」를 참조해 주세요.

추가 정보

일반 사용자

도입부 텍스트

기본 텍스트

레퍼런스

외부 링크

「」를 참조해 주세요.