양성자-양성자 사슬

Proton–proton chain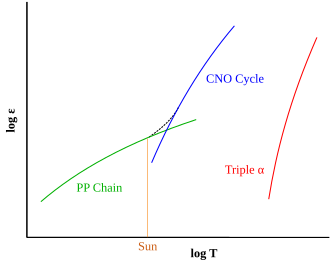
"pp 1"이 여기로 리디렉션됩니다. 기타 용도는 Pp1을 참조하십시오.
서로 다른 온도(T)에서 양성자-양성자(PP), CNO 및 삼중-α 융합 과정의 상대적 에너지 출력(ε)에 로그를 기록합니다. 파선은 별 내에서 PP와 CNO 과정의 결합된 에너지 생성을 보여줍니다. 태양의 중심부 온도 1550만 K에서는 PP 과정이 지배적입니다. PP 공정과 CNO 공정은 약 20 MK에서 동일합니다.[1]
양성자-양성자 가지 I 반응의 방식

양성자-양성자 사슬은 일반적으로 p-p 사슬이라고도 하며, 별이 수소를 헬륨으로 전환시키는 핵융합 반응의 두 가지 알려진 집합 중 하나입니다. 이는 태양 질량 이하의 항성에서 지배적인 반면,[2] 알려진 다른 반응인 CNO 사이클은 약 1.3 태양 질량 이상의 항성에서 지배적인 것으로 이론 모델에 의해 제시됩니다.[3]

일반적으로 양성자-양성자 융합은 양성자의 운동 에너지(온도)가 상호 정전기적 반발력을 극복할 수 있을 정도로 높을 경우에만 일어날 수 있습니다.[4]

태양에서, 듀테론을 생산하는 사건은 드물어요. 쌍성자는 항성 내에서 양성자-양성자 반응의 훨씬 더 일반적인 결과이며, 쌍성자는 거의 즉시 두 개의 양성자로 다시 붕괴됩니다. 수소가 헬륨으로 변환되는 속도가 느리기 때문에 처음에는 태양 중심부에서 수소가 완전히 변환되는 데 100억 년 이상이 걸릴 것으로 계산됩니다.[5]

때때로 "양성자-양성자 연쇄 반응"이라고 불리지만, 그것은 일반적인 의미에서의 연쇄 반응이 아닙니다. 대부분의 핵반응에서 연쇄반응은 핵분열 중에 방출되는 중성자와 같은 생성물을 생성하는 반응을 지정하며, 이 반응은 또 다른 그러한 반응을 빠르게 유도합니다. 양성자-양성자 사슬은 붕괴 사슬과 같은 일련의 반응입니다. 한 반응의 생성물이 다음 반응의 시작 물질입니다. 태양에는 수소에서 헬륨으로 이어지는 두 개의 주요 사슬이 있습니다. 하나의 사슬은 5개의 반응을 가지고 있고, 다른 하나의 사슬은 6개의 반응을 가지고 있습니다.

이론의 연혁

양성자-양성자 반응이 태양과 다른 별들이 타는 기본 원리라는 이론은 1920년대 아서 에딩턴에 의해 주창되었습니다. 당시 태양의 온도는 쿨롱 장벽을 극복하기에는 너무 낮은 것으로 여겨졌습니다. 양자역학이 개발된 후, 반발 장벽을 통해 양성자의 파동함수를 터널링하면 고전적인 예측보다 낮은 온도에서 융합이 가능하다는 사실이 밝혀졌습니다.

1939년에 한스 베테는 별의 다양한 반응의 비율을 계산하려고 시도했습니다. 두 개의 양성자가 결합하여 중수소 핵과 양전자를 얻는 것으로 시작하여 그는 양성자-양성자 사슬의 분지 II라고 부르는 것을 발견했습니다. 그러나 그는 우리가 지금 중요하게 알고 있는 두 개의 He 핵(분지 I)의 반응을 고려하지 않았습니다.[6] 이것은 1967년 베테가 노벨 물리학상을 수상한 항성 핵합성 연구의 일부였습니다.

양성자-양성자 사슬

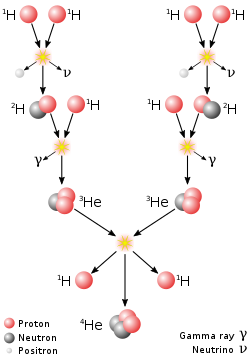
모든 가지의 첫 번째 단계는 두 개의 양성자를 중수소로 융합하는 것입니다. 양성자가 융합할 때 그 중 하나는 베타 플러스 붕괴를 겪으며 양전자와 전자 중성미자를[7] 방출하여 중성자로 변환됩니다. (비록 소량의 중수소 핵이 "펩" 반응에 의해 생성되지만, 아래를 참조하십시오.)

p + p → 2
1라
 		+
e+
 		+
ν
e 		+ 0.42 MeV

양전자는 환경의 전자와 함께 두 개의 감마선으로 소멸할 것입니다. 이 소멸과 중성미자의 에너지를 포함하여 순 반응은

p + p + e → D +
ν
e 		+ 1.442 MeV

(이는 PEP 반응과 동일합니다, 아래 참조) 1.442 MeV의 Q 값을 갖습니다.[7] 중성미자와 다른 생성물로 가는 에너지의 상대적인 양은 가변적입니다.

이것은 속도 제한 반응이며 약한 핵력에 의해 시작되기 때문에 매우 느립니다. 태양의 중심부에 있는 평균적인 양성자는 다른 양성자와 성공적으로 융합되기까지 90억 년을 기다립니다. 이 반응의 단면은 매우 낮기[8] 때문에 실험적으로 측정할 수는 없었지만 이론적으로 계산할 수 있습니다.[1]

첫 번째 단계에서 생성된 중수소는 다른 양성자와 융합하여 안정적이고 가벼운 헬륨 동위원소인 He를
생성할 수 있습니다.

2
1라
 		+ 1
1아
 		→ 3
2히
 		+
γ
 		+ 5.493 MeV

약력이 아닌 강한 핵력이 매개하는 이 과정은 첫 단계에 비해 매우 빠릅니다. 태양 중심부의 조건에서 새로 생성된 각각의 중수소 핵은 헬륨-3으로 변환되기 전까지 약 1초 정도만 존재할 것으로 추정됩니다.[1]

태양에서 이러한 반응에서 생성된 각각의 헬륨-3 핵은 헬륨-4로 변환되기 전까지 약 400년 동안만 존재합니다.[9] 헬륨-3가 생성되면 He를
생성하는 네 가지 경로가 가능합니다. p-p I에서 헬륨-4는 두 개의 헬륨-3 핵을 융합하여 생성됩니다. p-p II 및 p-p III 가지는 He와
기존 He를
융합하여 베릴륨-7을 생성하고, 추가 반응을 통해 두 개의 헬륨-4 핵을 생성합니다.

태양 에너지 출력의 약 99%는 다양한 p-p 사슬에서 발생하며, 나머지 1%는 CNO 순환에서 발생합니다. 태양의 한 모델에 따르면 다양한 p-p 가지에서 생성되는 He의
83.3%는 가지 I을 통해 생성되는 반면 p-p II는 16.68%와 p-p III 0.02%를 생성합니다.[1] 가지 II와 III에서 생성되는 중성미자의 절반이 첫 번째 단계(중성미자 합성)에서 생성되기 때문에 중성미자의 약 8.35%만이 이후 단계(아래 참조)에서 생성되고, 약 91.65%가 중성미자 합성에서 생성됩니다. 그러나 비슷한 시기에 만들어진 또 다른 태양 모형은 중성미자의 7.14%와 중수소 핵 합성의 92.86%만을 제공합니다.[10] 그 차이는 태양의 구성과 금속성에 대한 약간 다른 가정 때문인 것으로 보입니다.

극히 드문 p-p IV 가지도 있습니다. 다른 더 드문 반응이 발생할 수 있습니다. 이러한 반응의 비율은 단면적이 매우 작기 때문에 매우 낮거나 반응하는 입자의 수가 너무 적어 발생할 수 있는 반응은 통계적으로 유의하지 않습니다.

전반적인 반응은 다음과 같습니다.

4 1H+ + 2 e- → 4He2+ + 2 νe

26.73 MeV의 에너지를 방출하고, 그 중 일부는 중성미자에게 손실됩니다.

p-p I 분지

3
2히
 		+ 3
2히
 		→ 4
2히
 		+ 2 1
1H
 		+ 12.859 MeV

완전한 사슬은 26.732 MeV의[11] 순 에너지를 방출하지만 이 에너지의 2.2%(0.59 MeV)는 생성된 중성미자에게 손실됩니다.[12] p-p I 분지는 10~18 MK의 온도에서 우세합니다.[13] 10 MK 이하에서는 p-p 사슬이 느린 속도로 진행되어 He가
적게 생성됩니다.[14]

p-p Ⅱ 분기점

양성자-양성자 II 사슬
참고 항목: 리튬 연소
3
2히
 		+ 4
2히
 		→ 7
4비
 +
γ
 		+ 1.59 MeV
7
4비
 		+
e−
 		→ 7
3리
 +
ν
e 		+ 0.861 MeV / 0.383 MeV
7
3리
 		+ 1
1아
 		→ 2히4
2
 		+ 17.35 MeV

p-p II 분기는 18~25 MK의 온도에서 우세합니다.[13]

위의 두 번째 반응에서 에너지는 반응에 의해 생성되는 중성미자의 에너지임을 주목하십시오. Be와
Li의
반응에서 생성되는 중성미자의 90%는 0.861 MeV의 에너지를 가지고 있고, 나머지 10%는 0.383 MeV를 가지고 있습니다. 차이점은 생성된 리튬-7이 각각 접지 상태인지 여기 상태(전이 가능)인지 여부입니다. Be에서 안정한 Li로 방출되는 총 에너지는 약 0.862 MeV이며, 붕괴가 안정한 리튬으로 직접 간다면 중성미자에게 거의 모두 손실됩니다.

p-p Ⅲ 분기점

양성자-양성자 III 사슬
3
2히
 		+ 4
2히
 		→ 7
4비
 		+
γ
 		+ 1.59 MeV
7
4비
 		+ 1
1아
 		→ 8
5나
 		+
γ
8
5나
 		→ 8
4비
 		+
e+
 		+
ν
e
8
4비
 		→ 2
 히

이 사슬의 마지막 세 단계와 양전자 소멸은 총 18.209 MeV를 기여하지만 이 중 많은 부분은 중성미자에게 손실됩니다.

온도가 25 MK를 초과할 경우 p-p III 사슬이 우세합니다.[13]

p-p III 사슬은 태양의 주요 에너지원은 아니지만, 태양 중성미자 문제에서 매우 중요한 것은 매우 높은 에너지 중성미자(최대 14.06 MeV)를 생성하기 때문입니다.

p-p IV(Hep) 분기

이 반응은 이론적으로는 예측되지만 희귀성(태양에서 약 0.3ppm) 때문에 관찰된 적이 없습니다. 이 반응에서 헬륨-3는 양성자를 직접 포획하여 가능한 중성미자 에너지(최대 18.8 MeV[citation needed])가 더 높은 헬륨-4를 제공합니다.

3
2히
 		+ 1
1아
 		→ 4
2히
 		+
e+
 		+
ν
e

질량-에너지 관계는 이 반응과 그에 따른 소멸에 의해 방출되는 에너지에 대해 19.795 MeV를 제공하며, 그 중 일부는 중성미자에게 손실됩니다.

에너지 방출

최종 헬륨-4 원자의 질량과 네 개의 양성자의 질량을 비교하면 원래 양성자의 질량의 0.7%가 손실되었음을 알 수 있습니다. 이 질량은 각각의 개별 반응 동안 방출되는 생성된 입자, 감마선, 중성미자의 운동 에너지의 형태로 에너지로 변환되었습니다. 하나의 전체 체인의 총 에너지 수율은 26.73 MeV입니다.

감마선으로 방출되는 에너지는 전자와 양성자와 상호작용하여 태양 내부를 뜨겁게 달굴 것입니다. 또한 핵융합 생성물의 운동 에너지(예: 두 양성자와 p-p I 반응의 He
)는 태양의 플라즈마에 에너지를 더합니다. 이 가열은 태양의 중심부를 뜨겁게 유지시켜 마치 태양이 식어가는 것처럼 스스로의 무게로 붕괴되는 것을 막아줍니다.

중성미자는 물질과 크게 상호작용하지 않기 때문에 내부를 가열하지 않으므로 중력 붕괴로부터 태양을 지지하는 데 도움이 됩니다. 그들의 에너지는 손실됩니다: p-p I, p-p II, p-p III 사슬의 중성미자는 이러한 반응에서 각각 2.0%, 4.0%, 28.3%의 에너지를 운반합니다.[15]

다음 표는 중성미자에게 손실되는 에너지의 양과 세 갈래에서 나오는 "태양 광도"의 양을 계산한 것입니다. 여기서 "광도"란 태양이 중성미자가 아닌 전자기 방사선으로 방출하는 에너지의 양을 의미합니다. 사용된 시작 수치는 이 기사에서 더 높게 언급된 수치입니다. 이 표는 p-p 반응에서 나오는 99%의 힘과 중성미자에 관한 것이지 CNO 사이클에서 나오는 1%에 관한 것은 아닙니다.

태양에서의 광도 생성
분점 헬륨-4의 생산 비율 중성미자 생성으로 인한 손실 백분율 손실된 에너지의 상대적인 양 생성된 광도의 상대적인 양 총광도 백분율
지점 I 83.3 2 1.67 81.6 83.6
브랜치 II 16.68 4 0.67 16.0 16.4
브랜치 III 0.02 28.3 0.0057 0.014 0.015
총 100 2.34 97.7 100

PEP 반응

별의 양성자-양성자 및 전자 포획 반응

중수소는 희귀한 펩(양성자-전자-양성자) 반응(전자 포획)에 의해서도 생성될 수 있습니다.

1
1아
 		+
e−
 		+ 1
1아
 		→ 2
1라+
 		+
ν
e

태양에서 pep 반응 대 p-p 반응의 빈도비는 1:400입니다. 그러나 pep 반응에 의해 방출되는 중성미자는 훨씬 더 에너지가 넘칩니다: p-p 반응의 첫 번째 단계에서 생성되는 중성미자는 최대 0.42 MeV의 에너지 범위인 반면, pep 반응은 1.44 MeV의 날카로운 에너지 선 중성미자를 생성합니다. 이 반응에서 태양 중성미자가 검출된 것은 2012년 보렉시노(Borexino) 공동 연구에 의해 보고되었습니다.[16]

pep 및 p-p 반응은 모두 동일한 기본 상호작용의 두 가지 다른 파인만 표현으로 볼 수 있으며, 여기서 전자는 반응의 오른쪽으로 양전자로 전달됩니다. 이것은 NDM'06 웹사이트에서 볼 수 있는 별의 양성자-양성자 및 전자 포획 반응 그림에 나와 있습니다.[17]

참고 항목

참고문헌

  1. ^ a b c d Adelberger, Eric G.; et al. (12 April 2011). "Solar fusion cross sections. II. The pp chain and CNO cycles". Reviews of Modern Physics. 83 (1): 201. arXiv:1004.2318. Bibcode:2011RvMP...83..195A. doi:10.1103/RevModPhys.83.195. S2CID 119117147. 그림 2 참조. 캡션은 명확하지 않지만 백분율은 각 반응이 얼마나 일어나는지 또는 마찬가지로 각 가지에서 생성되는 헬륨-4의 양을 나타내는 것으로 확인되었습니다.
  2. ^ "The Proton–Proton Chain". Astronomy 162: Stars, Galaxies, and Cosmology. Archived from the original on 2016-06-20. Retrieved 2018-07-30.
  3. ^ Salaris, Maurizio; Cassisi, Santi (2005). Evolution of Stars and Stellar Populations. John Wiley and Sons. pp. 119–121. ISBN 0-470-09220-3.
  4. ^ Ishfaq Ahmad, The Nuclear, 1:42, 59, (1971), 양성자형-핵분열 반응.
  5. ^ 케네스 크레인, 핵물리학 입문, 와일리, 1987, p. 537
  6. ^ Hans Bethe (Mar 1, 1939). "Energy Production in Stars". Physical Review. 55 (5): 434–456. Bibcode:1939PhRv...55..434B. doi:10.1103/PhysRev.55.434.
  7. ^ a b Iliadis, Christian (2007). Nuclear Physics of Stars. Weinheim: Wiley-VCH. ISBN 9783527406029. OCLC 85897502.
  8. ^ Phillips, Anthony C. (1999). The Physics of Stars (2nd ed.). Chichester: John Wiley. ISBN 0471987972. OCLC 40948449.
  9. ^ 이 시간과 위의 다른 두 시간은 번, J. 중성자, 핵 및 물질, 도버 출판사, 미네올라, NY, 2011, ISBN 0486482383, p8에서 비롯됩니다.
  10. ^ Aldo Serenelli; et al. (Nov 2009). "New Solar Composition: The Problem With Solar Models Revisited". The Astrophysical Journal Letters. 705 (2): L123–L127. arXiv:0909.2668. Bibcode:2009ApJ...705L.123S. doi:10.1088/0004-637X/705/2/L123. S2CID 14323767. 표 3의 모델 AGSS09로부터 계산됩니다.
  11. ^ LeBlanc, Francis. An Introduction to Stellar Astrophysics.
  12. ^ Burbidge, E.; Burbidge, G.; Fowler, William; Hoyle, F. (1 October 1957). "Synthesis of the Elements in Stars". Reviews of Modern Physics. 29 (4): 547–650. Bibcode:1957RvMP...29..547B. doi:10.1103/RevModPhys.29.547.
  13. ^ a b c Iliadis, Christian (2015). Nuclear physics of stars (Second, revised and enlarged ed.). Weinheim, Germany. ISBN 978-3-527-33649-4. OCLC 908071061.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)
  14. ^ Adelberger, E. G.; et al. (2010). "Solar fusion cross sections. II. Theppchain and CNO cycles". Reviews of Modern Physics. 83: 195–245. arXiv:1004.2318. doi:10.1103/RevModPhys.83.195. S2CID 119117147.
  15. ^ 클라우즈 E. 롤프와 윌리엄 S. 로드니, 코스모스의 가마솥, 시카고 대학 출판부, 1988, 354쪽.
  16. ^ Bellini, G.; et al. (2 February 2012). "First Evidence of pep Solar Neutrinos by Direct Detection in Borexino". Physical Review Letters. 108 (5): 051302. arXiv:1110.3230. Bibcode:2012PhRvL.108e1302B. doi:10.1103/PhysRevLett.108.051302. PMID 22400925. S2CID 118444784.
  17. ^ 중성미자와 암흑물질에 관한 회의, 2006년 9월 7일, 세션 14.

외부 링크