후진 유도

역유도란 문제나 상황의 끝에서부터 최적의 행동의 순서를 결정하기 위해 시간적으로 거꾸로 추론하는 과정이다. 그것은 결정이 내려질 마지막 시점을 검토한 다음 그 순간에 어떤 행동이 가장 최적이 될 것인지를 확인하는 것으로 진행된다. 이 정보를 사용하여 결정의 두 번째에서 마지막 시간에 무엇을 해야 할지 결정할 수 있다. 이 과정은 모든 시점에서 가능한 모든 상황(즉, 모든 가능한 정보 집합)에 대한 최선의 조치를 결정할 때까지 뒤로 계속된다. 역유도는 1875년 악명 높은 장관 문제를 해결하려다 그 방법을 밝혀낸 아서 케일리에 의해 처음 사용되었다.^[1]

동적 프로그래밍의 수학적 최적화 방법에서 역유도는 벨만 방정식을 푸는 주요 방법 중 하나이다.^[2][3] 게임 이론에서 역유도란 순차 게임에서 서브게임 퍼펙트 평형을 계산하기 위해 사용하는 방법이다.^[4] 유일한 차이점은 최적화는 각 시점에서 무엇을 해야 할지를 선택하는 의사결정자를 한 명만 포함한다는 점이다. 반면에 게임 이론은 여러 플레이어의 결정이 어떻게 상호작용하는지를 분석한다. 즉, 각 상황에서 마지막 선수가 무엇을 할 것인가를 예측함으로써, 2대 1의 선수가 무엇을 할 것인가 등을 결정할 수 있다. 자동화된 계획 및 스케줄링과 자동화된 정리 증명이라는 관련 분야에서는 이 방법을 후진 검색 또는 후진 체인이라고 한다. 체스에서는 그것을 역행 분석이라고 부른다.

게임 이론의 분야가 존재해 온 이상, 게임을 해결하기 위해 역유도법을 사용해 왔다. 존 폰 노이만과 오스카 모겐스턴은 게임 이론을 연구 분야로 정립한 책인 '게임과 경제 행동 이론'(1944)에서 역유도 방식으로 제로섬을 풀자고 제안했다.^[5][6]

의사 결정 시 역방향 유도: 최적 정지 문제

10년 더 일할 수 있는 실업자를 생각해 보자 t = 1,2,...,10. 실업자로 남는 매년 100달러를 지불하는 '착한' 직업이나 44달러를 지불하는 '나쁜' 직업을 제안받았다고 가정해 보자면, 같은 확률(50/50)으로 말이다. 일단 그들이 일을 수락하면, 그들은 남은 10년 동안 그 직업에 남을 것이다. (단순히 그들은 그들의 금전적인 수입에만 신경을 쓰고, 서로 다른 시간에 수익을 동등하게 평가한다고 가정하면, 즉, 할인율은 1이다.)

이 사람은 나쁜 일을 받아들여야 하는가? 이 질문에 답하기 위해, 우리는 시간 t = 10부터 거꾸로 추론할 수 있다.

• 10시에 좋은 직업을 받아들이는 가치는 100달러, 나쁜 직업을 받아들이는 가치는 44달러, 이용할 수 있는 직업을 거부하는 가치는 0이다. 따라서 이들이 마지막 기간에도 여전히 실업자라면 그 당시 제시된 직장이 무엇이든 받아들여야 한다.
• 9시에 좋은 직장을 받아들이는 가치는 200달러(그 직장은 2년간 지속되기 때문에)이다; 나쁜 직장을 받아들이는 가치는 2*44달러 = 88달러다. 현재 구직 제의를 거절하는 가치는 0달러이고, 다음 구직 제의를 기다리는 가치는 50% 확률로 44달러가 되거나 50% 확률로 100달러가 될 것이며, 평균 0.5**(100+44) = 72달러가 될 것이다. 그러므로, 9시에 할 수 있는 일이 좋은지 나쁜지 상관없이, 더 좋은 제안을 기다리는 것보다 그 제안을 받아들이는 것이 더 낫다.
• 8시에, 좋은 직장을 받아들이는 것의 가치는 300달러(3년 동안 지속될 것이다), 나쁜 직장을 받아들이는 것의 가치는 3* 44달러 = 132달러다. 현재 구직 제의를 거절하는 가치는 $0이며, 게다가 9시에 구직 제의를 기다리는 가치도 있다. 우리는 이미 9시에 제안이 받아들여져야 한다고 결론을 내렸기 때문에, 9시에 구직 제의를 기다리는 예상가치는 0.5* (200+88달러) = 144달러다. 따라서 8시에는 나쁜 일을 받아들이는 것보다 다음 제안을 기다리는 것이 더 가치있다.

나쁜 제안은 9시나 10시까지 실업자가 있는 경우에만 받아들여져야 한다는 것을 계속해서 역행함으로써 확인할 수 있다; 그것들은 t = 8까지 항상 거절되어야 한다. 직관은 어떤 직장에서 오래 일하기를 기대한다면, 어떤 직업을 받아들여야 하는지에 대해 까다롭게 구는 것이 더 가치가 있다는 것이다.

이러한 종류의 동적 최적화 문제를 최적 중지 문제라고 하는데, 당면한 문제는 언제 더 나은 제안을 기다리는 것이 중단되어야 하는가에 관한 것이기 때문이다. 검색 이론은 쇼핑, 구직, 결혼과 같은 문맥에 이런 유형의 문제를 적용하는 미시경제학의 분야다.

게임 이론의 역유도

게임 이론에서 후진 유도는 해법 개념이다. 게임의 광범위한 형태 표현에서 개별 정보 세트에 민감한 합리성 개념의 정교화다.^[7] 역유도 아이디어는 주어진 게임 트리에서 각 정보에 대한 최적의 작용을 식별함으로써 순차적 합리성을 활용한다.

"전략: 조엘 왓슨의 게임 이론 소개, 역유도 절차는 다음과 같이 정의된다: " 게임을 처음부터 끝까지 분석하는 과정" 각 의사결정 노드에서, 후속 노드에서 식별된 조치의 플레이를 통해 도달할 수 있는 터미널 노드들을 고려할 때, 지배적인 모든 조치들을 고려하는 것으로부터 파업한다."^[8]

후발 유도 절차의 한 가지 단점은 제한된 등급의 게임에만 적용할 수 있다는 점이다. 그 절차는 효용성이 없는 완벽한 정보의 게임에 대해 잘 정의되어 있다. 넥타이를 매고 완벽한 정보로 승부하는 게임에도 잘 정의되고 의미가 있다. 그러나 둘 이상의 전략 프로파일로 이어진다. 이 절차는 비종교적인 정보 세트가 있는 일부 게임에 적용될 수 있지만 일반적으로 신뢰할 수 없다. 이 절차는 완벽한 정보로 게임을 해결하는데 가장 적합하다. 따라서, 모든 플레이어가 각 의사결정 노드에서 다른 플레이어의 행동과 보상에 대해 의식하지 않는다면, 역유도보다 더 쉽게 적용될 수 없다. (Watson pg.188)^[9]

후진 유도 절차는 간단한 예시로 증명할 수 있다.

게임 이론의 역유도 : 다단계 게임

제안된 게임은 2명이 참가하는 다단계 게임이다. 선수들은 영화를 보러 갈 계획이다. 현재 큰 인기를 끌고 있는 영화는 조커와 터미네이터 2편이다. 플레이어 1은 터미네이터를, 플레이어 2는 조커를 보고 싶어한다. 1번 선수는 먼저 티켓을 구입하고 2번 선수에게 자신의 선택에 대해 말할 것이다. 그러면 2번 선수가 티켓을 살 것이다. 둘 다 선택사항을 관찰하면, 그들은 영화를 보러 갈지 아니면 집에 있을지를 선택할 것이다. 첫 번째 스테이지와 마찬가지로 플레이어 1이 먼저 선택한다. 이어 2번 선수는 1번 선수의 선택을 관찰한 후 선택을 한다.

이 예에서는 보상이 서로 다른 단계에 걸쳐 추가된다고 가정한다. 그 게임은 완벽한 정보 게임이다.

정규 형식 행렬:

1단계

2번 선수 플레이어 1	조커	터미네이터
조커	3, 5	0, 0
터미네이터	1, 1	5, 3

2단계

2번 선수 플레이어 1	영화 보기	스테이 홈
영화 보기	6, 6	4, -2
스테이 홈	-2, 4	-2, -2

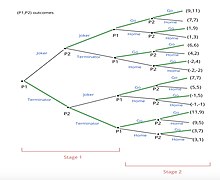
광범위한 형태 표현:

오른쪽에 보이는 대로 광범위한 형태를 갖춘 이 멀티 스테이지 게임을 해결하기 위한 단계:

1. 역방향 유도술은 마지막 마디부터 게임을 풀어나가기 시작한다.
2. 플레이어 2는 최종 노드에서 8개의 하위 게임을 관찰하여 "영화로 이동" 또는 "Stay Home"을 선택하십시오.
   1. 플레이어 2는 총 4개의 비교를 할 것이다. 그는 보수가 높은 옵션을 선택할 것이다.
   2. 예를 들어, 첫 번째 서브 게임을 고려하면 11의 보수는 7보다 높다. 따라서 플레이어 2는 "영화로 이동"을 선택한다.
   3. 그 방법은 모든 서브게임에 대해 계속된다.
3. 플레이어 2가 선택을 완료하면 플레이어 1은 선택한 하위 게임을 기반으로 선택을 하게 된다.
   1. 이 과정은 2단계와 유사하다. 1번 선수는 그녀의 선택을 위해 그녀의 보답을 비교한다.
   2. 이전 단계에서 플레이어 2가 선택하지 않은 서브게임은 최적이 아니기 때문에 두 선수 모두 더 이상 고려하지 않는다.
   3. 예를 들어, "영화 보러 가기"를 선택하면 9(9,11)의 보상이 주어지고, "Stay Home"을 선택하면 1(1,9)의 보상이 주어진다. 플레이어 1은 "영화로 이동"을 선택할 것이다.
4. 초기 노드에 도달할 때까지 각 플레이어에 대해 프로세스가 반복된다.
   1. 예를 들어, 플레이어 2는 11(9, 11)의 보수가 6(6, 6)의 "터미네이터"보다 크기 때문에 "조커"를 선택할 것이다.
   2. 예를 들어, 플레이어 1은 초기 노드에서 "터미네이터"를 선택할 것이다. 왜냐하면 그것은 11의 더 높은 보상을 제공하기 때문이다. 터미네이터: (11, 9) > 조커: (9, 11)
5. 서브게임 퍼펙트 평형을 파악하려면 각 정보 세트에서 최적의 서브게임을 선택하는 경로를 파악해야 한다.
   1. 이 예에서 플레이어 1은 "터미네이터"를 선택하고 플레이어 2도 "터미네이터"를 선택한다. 그리고 나서, 그들은 둘 다 "영화 보러"를 선택한다.
   2. 서브게임 퍼펙트 평형은 (11,9)의 보상으로 이어진다.

게임 이론의 역유도: 최후통첩 게임

역유도란 '끝에서 시작까지 게임을 분석하는 과정'이다. 다른 나시 에클리브리아에 대한 해결과 마찬가지로 플레이어의 합리성과 완전한 지식이 전제된다. 역방향 유도의 개념은 비록 그녀의 합리성이 그러한 노드에 도달하지 못할 것이라는 것을 암시하더라도, 그녀가 옵션을 선택할 때 각 결정 노드에 대해 합리적으로 행동하는 것이 상식이라는 가정에 해당한다.'^[10] 따라서 합리성의 상호 가정 하에 후진 유도는 각 플레이어가 게임의 모든 단계에서 상대가 무엇을 할 것인지를 정확하게 예측할 수 있게 한다.

역유도 서브게임 퍼펙트 평형을 풀기 위해서는 게임을 광범위한 형태로 작성한 뒤 서브게임으로 나눠야 한다. 첫 번째 노드, 즉 출발점에서 가장 멀리 떨어진 서브게임부터 이 서브게임에 대해 열거된 예상 보상에 무게를 두고 합리적인 플레이어가 스스로 더 높은 보상으로 옵션을 선택하게 된다. 가장 높은 지급 벡터를 선택하여 표시한다. 서브 게임에서 서브 게임까지 계속 역방향으로 작업하여 시작점에 도달할 때까지 서브 게임 완벽한 평형을 위해 해결하십시오. 이 과정이 진행됨에 따라, 당신의 초기의 광범위한 폼 게임은 점점 더 짧아질 것이다. 벡터의 눈에 띄는 경로는 서브게임 퍼펙트 평형이다.^[11]

최후통첩 게임에 적용된 후진 유도

1번 선수가 2번 선수와 1달러를 나누자고 제안하는 두 선수의 경기를 생각해 보라. 이것은 최후통첩 게임이라고 불리는 유명한 비대칭 게임이다. 플레이어가 적합하다고 생각되는 대로 달러를 분할하여 먼저 행동한다. 이제 2번 선수는 1번 선수가 처리한 부분을 받아들이거나 분할을 거부할 수 있다. 만약 선수 2가 스플릿을 수락한다면, 선수 1과 선수 2 모두 스플릿에 따라 보상을 받는다. 만약 두 선수가 1번 선수의 제안을 거절하기로 결정한다면, 두 선수 모두 아무것도 얻지 못할 것이다. 다시 말해서, 2번 선수는 1번 선수의 제안된 할당에 대해 거부권을 가지고 있지만 거부권을 적용하면 두 선수에 대한 보상이 없어진다.^[12] 따라서 이 게임의 전략 프로파일은 0과 1 사이의 모든 x에 대해 쌍(x, f(x))으로 작성할 수 있으며, 여기서 f(x)는 x의 허용 여부를 나타내는 양값 함수다.

제안이 $0보다 크다고 가정할 때 플레이어 1의 임의 제안이 있을 경우 플레이어 2의 선택과 응답을 고려하십시오. 후진 유도를 사용하면 확실히 우리는 선수 2가 0달러보다 크거나 같은 보답을 받아들이기를 기대할 것이다. 따라서, 선수 1은 선수 2에게 분할의 가장 큰 부분을 차지하기 위해 가능한 한 적게 줄 것을 제안해야 한다. 선수 1은 선수 2에게 가장 작은 단위를 주고 나머지는 선수 자신을 위해 보관하는 것이 특유의 서브게임 퍼펙트 평형이다. 최후통첩 게임은 서브게임 완벽하지 않기 때문에 역유도를 요구하지 않는 몇 개의 다른 나시 에클리브리아를 가지고 있다.

최후통첩 게임은 무한정 게임을 고려할 때 역유도의 유용성을 보여주는 사례지만, 이론적으로 예측한 게임의 결과물이 비판을 받는다. 경험적이고 실험적인 증거는 제안자가 거의 0달러를 제시하지 않는다는 것을 보여주었고 플레이어 2는 때때로 공정성을 이유로 0달러 이상의 제안을 거절하기도 했다. 선수 2에 의해 공정하다고 여겨지는 것은 상황에 따라 다르며, 다른 선수들의 압박이나 존재는 게임 이론 모델이 실제 사람들이 무엇을 선택할지 반드시 예측할 수 없다는 것을 의미할 수 있다.

실제로 서브게임 퍼펙트 평형이 항상 달성되는 것은 아니다. 미국의 행동경제학자 카메러에 따르면, 플레이어 2는 "아무것도 없이 끝나도 X의 20% 미만을 제안한다"고 거절한다.^[13] 대응자가 0과 같거나 큰 제안을 수용한다고 역유도할 수 있지만, 현실적으로 대응자들은 합리적인 참여자가 아니기 때문에 잠재적 금전적 이득보다는 '공정성' 제공에 더 신경을 쓰는 것 같다.

지네 게임을 참조하십시오.

경제학의 후진적 유도: 진입 결정 문제

플레이어가 업계의 현직 기업이고 해당 산업에 참여할 수 있는 잠재력이 있는 역동적인 게임을 고려해 보십시오. 현재 상태로는 현업자가 산업에 대한 독점권을 가지고 있으며 진입자에게 시장 점유율의 일부를 빼앗기고 싶지 않다. 진입자가 진입하지 않기로 선택할 경우, 현업자에 대한 보수가 높고(그것은 독점권을 유지하며), 진입자는 손실도 이득도 없다(그 보수는 0이다). 입회자가 들어오면 현직자가 입회자와 '싸우기' 또는 '취소'할 수 있다. 그것은 가격을 낮추고, 진입자를 폐업시키고, (그리고 퇴사 비용을 발생시키며 - 부정적인 보상으로) 자신의 이익을 손상시킴으로써 싸울 것이다. 진입자를 수용하면 매출의 일부를 잃게 되지만 높은 가격이 유지되고 가격을 낮추는 것보다 더 큰 이익을 얻는다(단독점 이익보다 낮음).

입회자가 입장할 경우 현직자의 최선의 대응이 수용하는 것인지 고려한다. 현직자가 수용하는 경우, 입회자의 최선의 대응은 입회(이윤을 얻는 것) 따라서 진입자가 진입하고 진입자가 진입할 경우 현직자가 수용하는 전략 프로파일은 역방향 유도와 일치하는 내시 평형이다. 다만, 현직자가 싸우려 할 경우 입회자의 최선의 대응은 입회하지 않는 것이며, 입회자가 입회하지 않을 경우 입회자가 입회하는 가상의 경우 입회자가 무엇을 선택하느냐는 중요하지 않다. 따라서 진입자가 진입할 경우 현직자가 싸우지만 진입자가 진입하지 않는 전략 프로파일도 내시 평형이다. 그러나 진입자가 이탈하여 진입할 경우 현직자의 최선의 대응책은 전투 위협은 신뢰할 수 없다는 점을 수용하는 것이다. 따라서 이 두 번째 나시 평형은 역방향 유도에 의해 제거될 수 있다.

각 의사결정 과정(하위 게임)에서 내시 평형을 찾는 것은 완벽한 하위 게임 평형으로서 구성된다. 따라서, 서브게임 퍼펙트 평형도를 나타내는 이러한 전략 프로파일은 진입자를 "허용"하는 데 사용되는 믿을 수 없는 위협과 같은 행동의 가능성을 배제한다. 만약 현직자가 진입자와 가격 전쟁을 시작하겠다고 위협한다면, 그들은 독점 가격에서 진입자 가격보다 약간 더 낮은 가격으로 그들의 가격을 낮추겠다고 위협하고 있는데, 이것은 비실용적이고, 만약 진입자가 가격 전쟁이 실제로 일어나지 않을 것이라는 것을 알고 있다면, 그것은 양측 모두에게 손실을 가져올 것이기 때문에 믿을 수 없을 것이다. 실현 가능하지 않거나 최적인 평형을 포함하는 단일 에이전트 최적화와는 달리, 서브게임 퍼펙트 평형은 다른 플레이어의 동작을 설명하기 때문에 실수로 서브게임에 도달하는 플레이어가 없도록 한다. 이 경우 완벽한 서브게임 평형을 제공하는 역방향 유도를 통해 진입자는 전략 프로파일에서 최선의 대응이 아니었다는 것을 알고 현직자의 위협을 확신하지 못하게 된다.^[14]

역유도 역설: 예상치 못한 교수형

예상치 못한 교수형 역설은 역유도와 관련된 역설이다. 수감자가 다음 주 월요일과 금요일 사이에 교수형을 당할 것이라는 말을 들었다고 가정해보자. 그러나 정확한 날은 깜짝 놀랄 것이다(즉, 그녀는 다음날 처형될 전날 밤을 모를 것이다). 사형수보다 더 똑똑한 죄수는 사형 집행일이 언제인지 결정하려고 한다.

그녀는 만약 그것이 목요일까지 일어나지 않았다면, 그녀는 그것이 금요일이 될 것이라는 것을 알았을 것이기 때문에 금요일에 그것이 일어날 수 없다는 이유를 들었다. 그러므로, 그녀는 가능한 한 금요일을 없앨 수 있다. 금요일이 없어지면 수요일이 아니면 목요일이 되어야 한다는 것을 알 수 있기 때문에 그녀는 목요일에 일어날 수 없다고 판단한다. 그러므로, 그녀는 목요일을 없앨 수 있다. 이 추론은 그녀가 모든 가능성을 없앨 때까지 계속된다. 그녀는 다음 주에 교수형을 당하지 않을 것이라고 결론짓는다.

놀랍게도, 그녀는 수요일에 교수형을 당했다. 그녀는 자신의 처형을 야기할 알려지지 않은 미래 요인이 그녀가 추론할 수 있는 것인지 확실히 알고 있다고 가정하는 실수를 저질렀다.

여기서 죄수는 역유도하여 이유를 대지만, 잘못된 결론에 도달하는 것 같다. 그러나 문제에 대한 설명은 역방향 유도를 수행하는 사람을 놀라게 하는 것이 가능하다고 가정한다는 점에 유의한다. 역유도 수학 이론은 이런 가정을 하지 않기 때문에 역설은 이 이론의 결과에 의문을 제기하지 않는다. 그럼에도 불구하고, 이 역설은 철학자들로부터 상당한 토론을 받았다.

합리성에 대한 역유도 및 상식

후진 유도는 두 플레이어가 모두 합리적일 때, 즉 항상 그들의 보상을 극대화하는 행동을 선택할 때에만 효과가 있다. 그러나 합리성은 충분하지 않다. 각각의 선수들은 다른 모든 선수들이 합리적이라고 믿어야 한다. 심지어 이것으로도 충분하지 않다: 각각의 선수들은 다른 모든 선수들이 이성적이라는 것을 알고 있다고 믿어야 한다. 애드 인피니텀도 그렇다. 즉 합리성은 상식이어야 한다.^[15]

제한적 후진 유도

제한적인 역유도란 완전히 합리적인 역유도로부터의 편차를 말한다. 그것은 완벽한 선견지명이 없는 역유도라는 규칙적인 과정을 제정하는 것을 포함한다. 이론적으로 이는 한 명 이상의 플레이어가 제한적인 선견지명을 가지고 모든 터미널 노드를 통해 역유도를 수행할 수 없을 때 발생한다.^[16] 제한된 후진 유도의 효과가 후기 게임 기간에 더 강력하기 때문에 제한된 후진 유도는 긴 게임에서 훨씬 더 큰 역할을 한다.

실험 결과, 센티페데 게임과 같은 순차적 흥정 게임에서 피험자는 이론적 예측에서 벗어나 대신 제한적인 후진 유도를 하는 것으로 나타났다. 이러한 편차는 플레이어들이 몇 단계 앞만 완벽하게 볼 수 있는 한정된 합리성의 결과로 발생한다.^[17] 이것은 결정의 예측 불가능성과 서브게임 퍼펙트 나시 평형도를 찾고 달성하는 비효율성을 허용한다.

이러한 현상에 대한 세 가지 광범위한 가설이 있다.

1. 사회적 요인의 존재(예: 공정성)
2. 비사회적인 요인의 존재(예: 제한적인 후진 유도)
3. 문화차이

역유도 위반은 주로 사회적 요인의 존재에 기인한다. 그러나 순차적 협상 게임(인지 계층 모델 활용)에 대한 데이터 기반 모델 예측은 일부 게임에서 제한적인 후진 유도 유도가 지배적인 역할을 할 수 있음을 강조해왔다.^[18]

반복적인 공공재 게임 내에서, 팀 행동은 제한된 후진 유도에 의해 영향을 받는다; 팀 구성원의 초기 기여도가 끝을 향한 기여보다 더 높다는 것이 명백하다. 제한된 후진 유도 또한 팀의 공공재 게임 내에서 얼마나 정기적으로 프리라이딩이 발생하는지에 영향을 미친다. 제한적인 후진 유도의 영향이 적은 초기에는 프리라이딩이 덜 빈번한 반면, 효과가 높을 때는 엔드 쪽으로 가면 프리 라이딩이 더 빈번해진다.^[19]

제한된 후방 유도 또한 경주 경기의 변종 내에서 테스트되었다. 게임에서 플레이어는 범위 내에서 순차적으로 정수를 선택하고 목표값에 도달할 때까지 자신의 선택을 합산한다. 그 선수는 과녁을 맞히면 상을 받고, 다른 선수는 패한다. 연이은 게임을 통해 작은 상이 소개되었다. 이어 대다수의 선수들이 원상보다는 소상을 위해 풀었기 때문에 제한적인 후진 유도를 했다. 출발할 때 두 상을 모두 고려하는 선수는 극소수에 불과했다.^[20]

메모들