관성 기준 프레임

이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가가 이해할 수 있도록 개선해 주세요.(2010년 9월) (이 템플릿메시지의 삭제 방법과 삭제 타이밍을 확인)

이 문서의 어조나 문체는 위키피디아에서 사용되는 백과사전적 어조를 반영하지 못할 수 있습니다. 더 나은 문서를 작성하려면 Wikipedia 가이드를 참조하십시오.(2018년 1월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

시리즈의 일부
고전 역학
$({displaystyle {textbf {F}}=squalfrac {d}{dt}})(m*textbf {v}})$ 운동 제2법칙
역사 타임라인 교재
나뭇가지 응용의 천상의 연속체 다이내믹스 운동학 동력학 스태틱스 통계
기초 액셀러레이션 각운동량 커플 달랑베르의 원리 에너지 동적인 잠재적인 힘. 기준범위 관성 기준 프레임 충동 관성/관성 모멘트 덩어리 기계력 기계 작업 순간. 모멘텀 공간 속도 시간을 토크 속도 가상 작업
제제 뉴턴의 운동 법칙 해석역학 라그랑주 역학 해밀턴 역학 루시아 역학 해밀턴-야코비 방정식 아펠 운동 방정식 쿱만-본 노이만 역학
주요 토픽 감쇠비 변위 운동 방정식 오일러의 운동 법칙 가공의 힘 마찰 고조파 발진기 관성/비관성 기준 프레임 평면 입자 운동 역학 움직임(선형) 뉴턴의 만유인력의 법칙 뉴턴의 운동 법칙 상대 속도 강체 역학 오일러 방정식 단순 고조파 운동 진동
회전 원운동 회전 기준 프레임 구심력 원심력 반응성 코리올리 힘 진자 접선 속도 회전 속도 각도 가속도/변위/주파수/속도
과학자 케플러 갈릴레오 호이겐스 뉴턴 경이다. 호록스 핼리 모페르튀이 다니엘 베르누이 요한 베르누이 오일러 달랑베르 클라이어트 라그랑주 라플라스 해밀턴 포아송 코시 러스 리우빌 어필 깁스 쿠프만 폰 노이만
물리 포털 카테고리
v t

고전 물리학과 특수 상대성 이론에서 관성 기준 프레임은 가속을 거치지 않는 기준 프레임입니다.관성 기준 프레임에서, 0의 순 힘이 작용하는 물리적 물체는 일정한 속도로 움직인다(이것은 0일 수 있다). 또는 동등하게, 뉴턴의 제1 운동 ^[1][2]법칙이 적용되는 기준 프레임이다.관성 기준 프레임은 분석 용어로 시간과 공간을 균일하게, 등방적으로, 그리고 시간에 의존하지 않는 ^[3]방식으로 기술하는 기준 프레임으로 정의할 수 있다.개념적으로 관성 프레임 내의 시스템의 물리에는 시스템 ^[4]외부의 원인이 없습니다.관성 기준 프레임은 관성 기준 프레임, 관성 프레임, 갈릴레이 기준 프레임 또는 관성 ^[5]공간이라고도 할 수 있습니다.

모든 관성 프레임이 서로에 대해 일정한 직선 운동 상태에 있다는 것을 유념하는 것이 중요합니다. 즉, 이들 중 하나와 함께 움직이는 가속도계가 제로 가속도를 감지합니다.하나의 관성 프레임에서의 측정은 단순한 변환(뉴턴 물리학에서의 갈릴레오 변환과 특수 상대성 이론에서의 로렌츠 변환)에 의해 다른 프레임에서의 측정으로 변환될 수 있다.일반 상대성 이론에서는 시공간과 조력의^[6] 곡률이 무시할 수 있을 정도로 작은 영역에서는 해당 영역을 ^[7][8]대략적으로 설명하는 일련의 관성 프레임을 찾을 수 있다.

고전물리학 및 특수상대성이론의 비관성기준범위에서 시스템의 물리학은 관성범위에 대한 그 프레임의 가속도에 따라 달라지며, 통상적인 물리력은 가공의 ^[9][10]힘에 의해 보충되어야 한다.반대로, 일반 상대성 이론의 시스템은 측지 운동 ^[11]원리 때문에 외부 원인을 가지고 있지 않습니다.예를 들어, 고전 물리학에서, 지구를 향해 떨어지는 공은 지구가 회전하고 있기 때문에 정확히 아래로 내려가지 않는데, 이것은 지구상의 관찰자의 기준 프레임이 관성적이지 않다는 것을 의미한다.물리학은 수평 운동을 예측하기 위해 코리올리 효과(이 경우 힘으로 간주)를 설명해야 합니다.기준 프레임의 회전과 관련된 가공력의 또 다른 예는 원심효과, 즉 원심력이다.

서론

물체의 움직임은 다른 물체, 관찰자 또는 시공간 좌표 집합과 같은 다른 것에 대해서만 설명할 수 있습니다.이를 참조 프레임이라고 합니다.좌표가 잘못 선택되면 운동 법칙이 필요 이상으로 복잡해질 수 있습니다.예를 들어, 외부 힘이 작용하지 않는 자유 물체가 어느 순간 정지해 있다고 가정합니다.많은 좌표계에서는 힘이 없어도 다음 순간부터 움직이기 시작합니다.그러나 기준 프레임은 항상 고정된 상태로 선택할 수 있습니다.마찬가지로, 공간이 균일하거나 독립적으로 설명되지 않는다면, 좌표계는 자유 물체의 우주 비행이 좌표계에서 복잡한 지그재그로 묘사될 수 있다.실제로 관성 프레임의 직관적인 요약을 제공할 수 있습니다. 관성 기준 프레임에서는 역학의 법칙이 가장 단순한 형태를 ^[3]취합니다.

관성 프레임에서는 뉴턴의 제1법칙인 관성의 법칙이 충족됩니다.자유 운동은 일정한 크기와 방향을 ^[3]가지고 있다.입자에 대한 뉴턴의 제2법칙은 다음과 같은 형태를 취합니다.

$\displaystyle \mathbf {F} = m\mathbf {a} \ , }$

F는 순 힘(벡터), m 입자의 질량 및 입자의 가속도(또한 벡터)로 프레임에 정지해 있는 관찰자에 의해 측정된다.힘 F는 접촉력, 전자기력, 중력 및 핵력과 같은 입자에 대한 모든 "실제" 힘의 벡터 합입니다.반대로, 회전 기준 프레임에서 축을 중심으로 각속도 δ로 회전하는 뉴턴의 두 번째 법칙은 다음과 같은 형태를 취한다.

$\displaystyle \mathbf {F} '=m\mathbf {a} \ , }$

이것은 관성 프레임에서와 동일하게 보이지만, 이제 힘 F f는 F뿐만 아니라 추가 항의 결과이다(이 방정식 아래의 단락은 상세한 수학 없이 주요 포인트를 나타낸다).

${\displaystyle \mathbf {F} '=\mathbf {F} - 2m \mathbf {v} \times \mathbf {v} _{B} - m\mathbf {x} _{B} \times \mathbf {B} \mathbf} \times (\mathbf {B})$

어디는 프레임의 각도 회전 벡터 Ω 회전축의 방향을 향하고, 광도로 회전 Ω의 각도율과 동일하게 나타냈습니다, 상징×, 벡터 xB 및 벡터 vB은 몸의 속도는 회전하는 관찰자 자세한 내용은 veloc에서 다른 것을 따라 몸을 담고 있는 벡터가 외적을 나타낸다.그것관성 관찰자에 의해 보이는 y).

힘 F'의 추가 항은 이 프레임에 대한 "가상" 힘이며, 그 원인은 프레임 내의 시스템 외부에 있습니다.첫 번째 추가 항은 코리올리 힘, 두 번째 항은 원심력, 세 번째 항은 오일러 힘입니다.이들 항은 모두 다음과 같은 특성을 가지고 있다: δ = 0일 때 사라진다. 즉, 관성 프레임은 0이다(물론 회전하지 않는다). 이들은 δ의 특정 값에 따라 모든 회전 프레임에서 다른 크기와 방향을 취한다. 그들은 회전 프레임에 유비쿼터스하다(상황에 관계없이 모든 입자).ance); 식별 가능한 물리적 선원, 특히 물질에 명백한 선원이 없다.또한 가상의 힘은 (예를 들어 핵력이나 전기력과 달리) 거리에 따라 떨어지지 않는다.예를 들어 회전 프레임의 회전축에서 발생하는 것처럼 보이는 원심력은 축으로부터의 거리에 따라 증가합니다.

모든 관찰자는 실제 힘에 동의하며, 비관성 관찰자만이 가상의 힘을 필요로 한다.관성 프레임의 물리 법칙은 불필요한 힘이 존재하지 않기 때문에 더 간단하다.

뉴턴의 시대에는 고정된 별들이 기준 프레임으로 호출되었고, 아마도 절대 공간에 상대적으로 정지해 있을 것이다.고정된 별에 대해 정지해 있거나 이 별들에 대해 균일한 번역으로 되어 있는 기준 프레임에서 뉴턴의 운동 법칙은 유지되어야 했다.반면 고정별에 대해 가속하는 프레임(고정별에 대해 회전하는 프레임)에서 운동 법칙은 가장 단순한 형태로 유지되지 않고 예를 들어 코리올리 힘과 원심력 같은 가공의 힘을 더함으로써 보완되어야 했다.뉴튼은 어떻게 이러한 힘이 발견될 수 있는지를 증명하기 위해 두 가지 실험을 고안했고, 따라서 관찰자에게 그것들이 관성 프레임에 있지 않다는 것을 밝혀냈다. 즉, 무게 중심을 중심으로 회전하는 두 개의 구를 연결하는 코드의 장력의 예와 회전하는 양동이의 물 표면 곡률의 예.두 경우 모두, 원심력과 코리올리의 힘이 관측치를 설명하지 않으면 뉴턴의 제2법칙은 회전하는 관찰자에게 효과가 없을 것이다(구체의 경우 장력, 회전하는 버킷의 경우 포물선 수면).

우리가 지금 알고 있듯이, 고정된 별들은 고정되어 있지 않다.우리 은하에 있는 은하들은 은하와 함께 방향을 틀며 적절한 움직임을 보인다.우리 은하 밖에 있는 은하들(예: 한때 별로 오인된 성운)도 그들 자신의 운동에 참여하는데, 이는 부분적으로 우주의 팽창 때문이기도 하고, 일부는 특이한 ^[12]속도 때문이기도 합니다.안드로메다 은하는 ^[13]우리 은하와 초당 117km의 속도로 충돌하고 있습니다.관성 기준 프레임의 개념은 더 이상 고정된 별이나 절대 공간에 얽매이지 않는다.오히려 관성 프레임의 식별은 프레임 내의 물리 법칙의 단순성에 기초한다.특히, 가상의 힘의 부재는 그들의 ^[14]식별 특성이다.

실제로는 요건은 아니지만, 고정된 별에 기초한 기준 프레임을 관성 기준 프레임인 것처럼 사용하면 불일치가 거의 발생하지 않는다.예를 들어, 태양의 회전으로 인한 지구의 원심 가속도는 은하 ^[15]중심에 대한 태양의 원심 가속도의 약 3천만 배입니다.

더 자세히 설명하기 위해 "우리의 우주는 회전합니까?"라는 질문을 생각해 보십시오.이에 답하기 위해,^[16] 우리는 물리 법칙을 사용하여 은하수의 모양을 설명하려고 시도할 수 있습니다. 다른 관측은 더 확정적일 수 있습니다. 즉, 마이크로파 배경 복사나 빅뱅 핵 ^[17][18]합성의 이방성 같은 더 큰 불일치 또는 더 적은 측정 불확실성을 제공합니다.우리 은하의 평탄도는 관성 기준 범위에서의 회전 속도에 따라 달라집니다.만약 우리가 그것의 겉보기 회전 속도를 전적으로 관성 프레임의 회전으로 본다면, 우리가 실제로 이 회전의 일부가 우주의 회전 때문이고 은하 자체의 회전에는 포함되지 않아야 한다고 가정할 때와는 다른 "평탄도"가 예측된다.물리 법칙에 근거해, 하나의 매개변수가 우주의 회전 속도인 모델이 설정됩니다.물리 법칙이 회전하는 모델보다 회전하는 모델의 관측과 더 정확하게 일치한다면, 우리는 다른 모든 관련 실험 관찰에 따라 회전에 가장 적합한 값을 선택하는 경향이 있다.회전 파라미터의 값이 성공적이지 않고 이론이 관측오차 이내가 아닌 경우, 예를 들어 은하회전곡선을 설명하기 위해 암흑물질의 수정을 고려한다.지금까지 관찰된 바에 따르면 우주의 회전 속도는 6×10년에¹³ 한 번(10rad/^[19]yr)보다⁻¹³ 빠르지 않고 매우 느리며, 회전 여부에 대한 논란은 계속되고 있다.하지만, 만약 회전이 발견된다면, 우주와 연결된 프레임의 관측치 해석은 고전 물리학과 특수 상대성 이론에서 그러한 회전에 내재된 가상의 힘에 대해 수정되거나, 일반 상대성 이론에서 시공간 곡률 및 측지학에서의 물질의 움직임으로 해석되어야 할 것이다.

양자 효과가 중요한 경우, 양자 참조 프레임에서 추가적인 개념적 복잡성이 발생합니다.

배경

물리 법칙이 간단한 프레임 세트

특수상대성이론의 첫 번째 가설에 따르면, 모든 물리 법칙은 관성 프레임에서 가장 단순한 형태를 취하며, 균일한 변환에 의해 상호 연관된 여러 관성 프레임이 존재한다.

특수 상대성 원리:좌표계 K가 물리법칙이 가장 단순한 형태로 유효하도록 선택되면 K에 대해 균일한 번역으로 이동하는 다른 좌표계 K'에 대해서도 동일한 법칙이 유효하다.

--

이러한 단순성은 관성 프레임이 외부 원인 없이 자급자족적인 물리학을 갖는 반면 비관성 프레임의 물리학은 외부 ^[4]원인을 갖는다는 점에서 나타난다.단순성의 원리는 뉴턴 물리학뿐만 아니라 특수 상대성 이론에서도 사용될 수 있습니다. 나겔과^{[21] [22]}블라고예비치도 참조하십시오.

뉴턴 역학의 법칙이 항상 가장 단순한 형태로 유지되는 것은 아니다.예를 들어 관찰자가 지구를 기준으로 회전하는 원반 위에 놓이면 관찰자는 다른 물체와의 상호작용에 의해 야기되지 않는 디스크 주위를 향해 자신을 밀어내는 '힘'을 감지하게 된다.여기서 가속도는 일반적인 힘의 결과가 아니라 소위 관성력의 결과입니다.뉴턴의 법칙은 관성 프레임이라고 불리는 기준 프레임의 패밀리에서만 가장 단순한 형태로 유지됩니다.이 사실은 갈릴레이 상대성 원리의 본질을 나타냅니다.
역학의 법칙은 모든 관성 프레임에서 동일한 형태를 가집니다.

--

실제로 관성 기준 프레임의 등가성은 균일하게 움직이는 상자 안의 과학자들이 어떤 실험에서도 절대 속도를 결정할 수 없다는 것을 의미합니다.그렇지 않으면, 그 차이로 인해 절대 표준 ^[23][24]기준 프레임이 설정될 것입니다.이 정의에 따르면, 빛의 속도의 항상성으로 보충되는 관성 기준 프레임은 로렌츠 변환이 ^[25]부분군인 대칭 변환의 푸앵카레 그룹에 따라 서로 변환된다.뉴턴 역학에서, 빛의 속도가 무한대인 특수 상대성 이론의 한계 사례로 볼 수 있는 관성 기준 프레임은 갈릴레오 대칭 그룹에 의해 관련된다.

절대 공간

뉴턴은 고정된 별에 대해 고정된 기준 프레임에 의해 잘 근사된 것으로 여겨지는 절대 공간을 가정했다.관성 프레임은 절대 공간에 대해 균일한 변환의 프레임이었다.하지만, 심지어 뉴턴의 시대에도^[26] 일부 과학자들은 절대 공간이 공식의 결함이며 대체되어야 한다고 느꼈다.

실제로 관성 기준의 표현(독일어:관성계)는 1885년 루드비히 랑게에 의해 "절대 시공간"에 대한 뉴턴의 정의를 보다 작동 가능한 ^[27][28]정의로 대체하기 위해 만들어졌다.Iro가 번역한 바와 같이 Lange는 다음과 같은 ^[29]정의를 제안했습니다.

3개의 다른(비공평면) 방향으로 같은 지점에서 던져진 질량점이 던져질 때마다 직선 경로를 따라가는 기준 프레임을 관성 프레임이라고 합니다.

Lange의 제안에 대한 논의는 ^[26]Mach에서 찾을 수 있다.

뉴턴 역학에서 "절대 공간"이라는 개념의 부적절성은 블라고예비치에 의해 ^[30]설명된다.

• 절대 공간의 존재는 갈릴레이의 상대성 원리에 따르면 어떤 관성 프레임도 골라낼 수 없기 때문에 고전 역학의 내부 논리와 모순된다.
• 절대 공간은 관성 프레임 중 하나와 관련된 가속도와 관련이 있기 때문에 관성력을 설명하지 않는다.
• 절대 공간은 물리적인 물체의 가속에 대한 저항을 유도하여 작용하지만 작용하지는 않습니다.

--

특수 상대성 ^[31]이론에서는 연산 정의의 효용이 훨씬 더 많이 다루어졌다.DiSalle은 Lange의 정의를 포함한 역사적 배경을 다음과 같이 ^[32]요약하고 있다.

"운동의 법칙은 어떤 기준 프레임을 가지고 있는가?"라는 원래의 질문은 잘못된 것으로 드러났습니다.운동의 법칙은 기본적으로 기준 프레임의 클래스와 (원칙적으로) 기준 프레임을 구성하는 절차를 결정한다.

--

뉴턴의 관성 기준계

뉴턴 역학의 영역에서 관성 기준 프레임 또는 관성 기준 프레임은 뉴턴의 운동 제1법칙이 ^[33]유효한 프레임입니다.하지만, 특수 상대성 이론의 원리는 단순히 뉴턴의 제1법칙이 아닌 모든 물리법칙을 포함하도록 관성 프레임의 개념을 일반화한다.

뉴턴은 첫 번째 법칙을 고정된 ^[34]별에 대해 일정한 운동을 하는 기준 프레임, 즉 별에 대해 회전하거나 ^[35]가속하지 않는 것으로 보았다.오늘날 "절대 공간"의 개념은 버려지고 고전 역학 분야의 관성 프레임은 다음과 ^[36][37]같이 정의됩니다.

관성 기준 프레임은 힘의 영향을 받지 않는 입자의 움직임이 일정한 속도로 직선상에 있는 프레임이다.

따라서 관성 프레임과 관련하여, 물체나 물체는 물리적인 힘이 가해질 때만 가속되며 (뉴턴의 제1법칙에 따라) 순 힘이 없을 때 정지해 있고 움직이는 물체는 균일하게, 즉 직선과 일정한 속도로 계속 움직일 것이다.뉴턴 관성 프레임은 갈릴레오 대칭 그룹에 따라 서로 변환됩니다.

이 규칙이 직선 운동이 제로 순력임을 나타내는 것으로 해석되는 경우, 이 규칙은 다양한 프레임에서 직선 운동을 관찰할 수 있기 때문에 관성 기준 프레임을 식별하지 않는다.규칙이 관성 프레임을 정의하는 것으로 해석될 경우, 우리는 제로 순 힘이 적용되는 시기를 결정할 수 있어야 한다.아인슈타인은 ^[38]이 문제를 요약했다.

관성 원리의 약점은 원 안에서 논쟁하는 것이다: 질량이 다른 물체와 충분히 떨어져 있으면 가속 없이 움직인다; 우리는 질량이 가속 없이 움직인다는 사실만으로 다른 물체와 충분히 떨어져 있다는 것을 안다.

--

이 문제에는 몇 가지 접근법이 있습니다.한 가지 접근법은 모든 실제 힘이 알려진 방식으로 그들의 근원으로부터 떨어져 나간다고 주장하는 것입니다. 그래서 우리는 힘이 ^[39]존재하지 않는다는 것을 확실히 하기 위해 물체가 모든 근원에서 충분히 멀리 떨어져 있다는 것을 확신하기만 하면 됩니다.이 접근법의 가능한 문제점은 먼 우주가 문제에 영향을 미칠 수 있다는 역사적으로 오랜 시각이다.또 다른 접근법은 실제 힘에 대한 모든 실제 출처를 식별하고 이를 설명하는 것이다.이 접근법의 가능한 문제는 마하의 원리와 우주에 대한 불완전한 이해로 인해 우리가 무언가를 놓치거나 그들의 영향을 부적절하게 설명할 수 있다는 것입니다.세 번째 접근법은 기준 프레임을 이동할 때 힘이 변환되는 방식을 살펴보는 것입니다.프레임의 가속에 의해 발생하는 가공의 힘은 관성 프레임에서 사라지며, 일반적인 경우 복잡한 변환 규칙을 가지고 있습니다.물리 법칙의 보편성과 법칙이 가장 단순하게 표현되는 프레임에 대한 요청에 기초하여 관성 프레임은 그러한 가공의 힘이 없는 것으로 구별된다.

뉴턴은 ^[40][41]운동법칙의 결과 중 하나로 상대성 원리를 설명했다.

주어진 공간에 포함된 물체의 움직임은 그 공간이 정지되어 있든 직선으로 균일하게 앞으로 이동하든 간에 서로 동일하다.

--

이 원리는 두 가지 면에서 특수 원리와 다릅니다. 첫째, 기계학으로 제한되고 둘째, 단순성에 대한 언급이 없습니다.그것은 서로 번역된 참조 ^[42]프레임 간에 설명 형식의 불변성을 특수 원리와 공유한다.기준 프레임을 분류할 때 가상의 힘의 역할은 아래에서 더 추구된다.

뉴턴 역학

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2018년 5월) (이 템플릿메시지를 삭제하는 방법과 시기에 대해 알아보기)

갈릴레오 변환을 사용하는 고전 이론은 모든 관성 기준 프레임의 동등성을 가정합니다.어떤 이론들은 절대적인 공간과 절대적인 시간을 제공하는 특권적인 프레임의 존재를 가정할 수도 있다.갈릴레오 변환은 좌표를 간단히 추가하거나 빼서 하나의 관성 기준 $프레임$인 s$\$에서 다른 $s{\displaystyle {\mathbf{}}^{}}$δ(\$displaystyle \mathbf {s} ^{\prime$로 변환합니다.

${\displaystyle \mathbf {r}^{\prime}=\mathbf {r} -\mathbf {r} _{0}-\mathbf {v} t}$

${\displaystyle t^{\prime}=t-t_{0}}$

여기서₀ r과₀ t는 공간과 시간의 원점 변화를 나타내고 v는 두 관성 기준 프레임의 상대 속도를 나타낸다.갈릴레오 변환에서 두 사건 사이의 시간₂ t - t는₁ 모든 기준 프레임에서 동일하며 두 사건 사이의 거리(또는 등가물체의 길이₂ r - r₁ )도 동일하다.

특수상대성이론

뉴턴 역학과 마찬가지로 아인슈타인의 특수 상대성 이론은 모든 관성 기준 프레임의 등가성을 가정한다.그러나 특수상대성이론은 자유공간에서의 빛의 속도가 불변하다고 가정하기 때문에 관성 프레임 사이의 변환은 뉴턴 역학에서 사용되는 갈릴레오 변환이 아니라 로렌츠 변환이다.빛의 속도의 불변성은 시간 연장 및 길이 수축, 동시성의 상대성과 같은 반직관적인 현상으로 이어지며,^[43] 이는 실험적으로 광범위하게 검증되었다.Lorentz 변환은 빛의 속도가 무한대에 가까워지거나 프레임 간의 상대 속도가 ^[44]0에 가까워지면 갈릴레오 변환으로 감소합니다.

일반상대성이론

일반상대성이론은 동등성의 ^[45][46]원리에 기초한다.

가속도가 중력 때문인지 기준 프레임이 가속 중인지 구별하기 위해 수행할 수 있는 실험 관찰자는 없습니다.

--

이 아이디어는 아인슈타인의 1907년 논문 "상대성과 중력의 원리"에 소개되었고 이후 ^[47]1911년에 개발되었다.이 원리에 대한 지지는 크기나 조성에 관계없이 중력 질량에 대한 관성 비율이 모든 물체에 동일한지 여부를 결정하는 외트뵈스 실험에서 찾을 수 있다.현재까지 ^[48]10개 부품¹¹ 중 몇 개 부품에서 차이가 발견되지 않았습니다.실험 현장 주변의 국부 질량 분포(외트뵈스 자체의 질량에 대한 힌트 포함)와 같은 외트뵈스 실험의 미묘한 부분에 대한 약간의 논의는 ^[49]프랭클린을 참조한다.

아인슈타인의 일반 이론은 특수 상대성 이론의 "평탄한" 민코프스키 공간을 0이 아닌 곡률을 내는 측정법으로 대체함으로써 명목상 "관성" 효과와 "비관성" 효과 사이의 차이를 수정한다.일반 상대성 이론에서 관성의 원리는 시공간 곡률에 의해 지시된 방식으로 물체가 움직이는 측지 운동 원리로 대체된다.이 곡률의 결과로, 서로에 대해 특정한 속도로 움직이는 관성 물체는 일반 상대성 이론에서 주어진 것이 아니다.이 측지선 편차의 현상은 뉴턴 역학과 특수 상대성 이론에서처럼 관성 기준 프레임이 전지구적으로 존재하지 않는다는 것을 의미한다.

그러나, 일반 이론은 곡률 효과가 덜 중요해지고 이전의 관성 프레임 원칙이 다시 ^[50][51]작동할 수 있는 시공간에서 충분히 작은 영역에 걸쳐 특수 이론으로 감소한다.결과적으로, 현대의 특수 상대성 이론은 때때로 단지 "지역 이론"^[52]으로 묘사된다.예를 들어, "국소"는 전체 은하를 포함할 수 있습니다.천문학자 Karl Schwarzschild는 서로를 공전하는 쌍성들의 움직임을 관찰했다.그는 그러한 계의 두 개의 별들의 궤도가 평면상에 있고, 두 개의 별들의 궤도 근일점은 태양계에 대해 같은 방향을 가리키고 있다는 것을 발견했다.슈바르츠실트는 그것이 변함없이 보여졌다고 지적했다. 즉, 관측된 모든 이중성계의 각운동량 방향은 태양계의 각운동량 방향에 대해 고정된 상태를 유지하고 있다.이러한 관측을 통해 그는 은하 내부의 관성 프레임이 서로에 대해 회전하지 않으며, 은하수의 공간은 대략 갈릴레오 또는 ^[53]밍코우스키안이라고 결론을 내릴 수 있었습니다.

예

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2013년 7월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

간단한 예

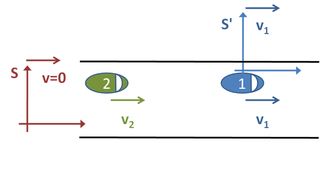
일상 생활에서 흔히 볼 수 있는 상황을 생각해 보세요.두 대의 차가 도로를 따라 이동하며, 둘 다 일정한 속도로 움직인다.그림 1을 참조해 주세요.어느 순간, 그들은 200미터씩 떨어져 있다.앞차는 초속 22미터로 달리고 뒤차는 초속 30미터로 달리고 있습니다.두 번째 차량이 첫 번째 차량을 따라잡는 데 얼마나 걸릴지 알아보려면 세 가지 확실한 "기준 프레임"을 선택할 수 있습니다.

우선, 우리는 길가에서 두 대의 차를 관찰할 수 있었다."기준 프레임" S는 다음과 같이 정의한다.우리는 길가에 서서 두 번째 차가 우리를 통과하는 정확한 순간(공교롭게도 거리 d=200m 떨어져 있을 때)부터 정지를 시작합니다.어느 차량도 가속하지 않으므로 다음 공식으로 위치를 확인할 수 있습니다. ${\displaystyle {여기}_{}}$서 x${\displaystyle {}_{}}$${\displaystyle {1\mathrm{}}_{}}$ (${\displaystyle t}$) {$displaystyle x_{1}(t)}$은 시간 t 이후의 차량 미터 단위 $위치$이고${\displaystyle {}_{}}$x ${\displaystyle 2}$( t$$) {$displaystyle x_{2$}(t$$$)$는 시간 t 이후의 차량 위치입니다.

${\displaystyle x_{1}(t)=d+v_{1}t=200+22t,\display x_{2}(t)=v_{2}t=30t}$

이러한 공식은 t = 0초에서 첫 번째 차량이 200m 아래에 있고 두 번째 차량이 예상대로 우리 바로 옆에 있음을 예측한다.${\displaystyle {x\mathrm{}}_{}}$ 1 $=$ ${\displaystyle {}_{}}$ $({$}=$x_{$2$\})$의 시간을 찾고 싶기 때문에 ${\displaystyle {x\mathrm{}}_{}}$ 1 $=$ ${\displaystyle {}_{}}$({$style x_{1$}=$x_{2})$로 $설정$하고 t ${{displaystyle$ t$\}$에 대해 해결합니다.

${\displaystyle 200+22t=30t,}$

${\displaystyle 8t=200,}$

${\displaystyle t=25\\mathrm {seconds} .}$

또는 첫 번째 차량에 위치한 기준 S' 프레임을 선택할 수 있습니다.이 경우, 첫 번째 차량은 정지해 있고 두 번째 차량은 v - v₁ = 8 m/s의 속도로₂ 뒤에서 접근하고 있다.주문 차를 따라잡기.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw의 시간이 걸릴 것이다.-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}d/v2 − v1)200/8 s, 즉 25초 전처럼.적절한 기준 프레임을 선택하면 문제가 얼마나 쉬워지는지 알 수 있습니다.세 번째 가능한 기준 프레임은 두 번째 차량에 부착됩니다.이 예는 두 번째 차량이 정지해 있고 첫 번째 차량이 8m/s의 속도로 차량 쪽으로 후진한다는 점을 제외하면 방금 설명한 사례와 유사하다.

회전하고 가속하는 기준 프레임을 선택하여 복잡한 방식으로 이동할 수 있었지만, 이는 문제를 불필요하게 복잡하게 만들었을 것입니다.또한 한 좌표계에서 측정된 값을 다른 좌표계로 변환할 수 있습니다.예를 들어, 시계가 현지 표준 시간보다 5분 빠르게 실행된다고 가정합니다.만약 당신이 이 사실을 안다면, 누군가 당신에게 지금이 몇 시냐고 물었을 때, 당신은 정확한 시간을 얻기 위해 당신의 시계에 표시된 시간으로부터 5분을 공제할 수 있다.따라서 관찰자가 시스템에 대해 수행하는 측정은 관찰자의 기준 프레임에 따라 달라집니다(버스가 3시 5분에 도착했다고 말할 수 있으며, 실제로는 3시에 도착했다고 말할 수 있습니다).

추가 예시

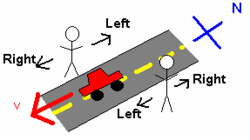
두 관찰자의 방향만 관련된 간단한 예에서는 두 사람이 북쪽과 남쪽 거리의 양쪽에 서로 마주보고 서 있다고 가정해 보십시오.그림 2를 참조해 주세요.차 한 대가 남쪽으로 향해서 그들을 지나간다.동쪽을 바라보고 있는 사람에게는 차가 오른쪽으로 움직이고 있었다.하지만 서쪽을 바라보고 있는 사람에게는 차가 왼쪽으로 움직이고 있었다.이 불일치는 두 사람이 이 시스템을 조사하기 위해 두 개의 서로 다른 참조 프레임을 사용했기 때문입니다.

상대적인 움직임을 관찰하는 관찰자를 포함하는 더 복잡한 예로는 알프레드가 길가에 서서 왼쪽에서 오른쪽으로 차가 자신을 지나치는 것을 지켜본다고 생각해 봅시다.Alfred는 기준 프레임에서 자신이 서 있는 지점을 원점으로, 도로를 X축으로, 전방 방향을 양의 Y축으로 정의합니다.그에게 자동차는 x축을 따라 약간의 속도 v를 양의 x방향으로 이동한다.알프레드의 기준 프레임은 가속하지 않기 때문에 관성 기준 프레임으로 간주됩니다(지구 자전 및 중력 등의 효과를 무시합니다).

이제 차를 운전하는 벳시를 생각해보자.기준 프레임을 선택할 때 Betsy는 자신의 위치를 원점으로, 오른쪽 방향을 양의 x축으로, 앞에 있는 방향을 양의 y축으로 정의합니다.이 기준 프레임에서 움직이는 것은 정지해 있는 벳시(Betsy)와 주변 세계입니다.예를 들어 알프레드를 지나칠 때 그는 음의 y 방향으로 속도 v로 움직이는 것을 관찰합니다.그녀가 북쪽으로 운전할 경우 북쪽은 양의 Y 방향이고, 동쪽으로 돌면 동쪽이 양의 Y 방향이 됩니다.

마지막으로, 비관성 관찰자의 예로 캔디스가 차를 가속시키고 있다고 가정해 봅시다.그녀가 그의 옆을 지날 때 알프레드는 그녀의 가속도를 측정했고 그것이 음의 x 방향의 a임을 발견한다.캔디스의 가속도가 일정하다고 가정할 때, 벳시는 어떤 가속도를 측정합니까?만약 벳시의 속도 v가 일정하다면, 그녀는 관성 기준 프레임에 있고, 그녀는 그녀의 기준 프레임에서 알프레드와 같은 가속도를 찾을 것이다, 음의 y 방향의 a.그러나 음의 y 방향으로 속도 A로 가속하는 경우(즉, 감속), Candace의 가속도는 음의 y 방향으로 aθ = a - A로 Alfred가 측정한 값보다 작습니다.마찬가지로, 양의 Y 방향으로 속도 A로 가속하는 경우(수직 상승), 음의 Y 방향으로 속도 aθ = a + A로 Candace의 가속도를 관찰합니다. 이는 Alfred의 측정값보다 큰 값입니다.

기준 프레임은 특수 상대성 이론에서 특히 중요합니다. 왜냐하면 기준 프레임이 빛의 속도의 상당한 비율로 움직일 때, 그 프레임의 시간의 흐름이 반드시 다른 프레임에 적용되는 것은 아니기 때문입니다.빛의 속도는 움직이는 기준 프레임 사이의 유일한 진정한 상수로 간주됩니다.

언급

다양한 기준 관성 프레임에 대해 위에서 설명한 몇 가지 가정에 주목하는 것이 중요하다.예를 들어, 뉴턴은 다음 예에서 설명하듯이, 세계 시간을 사용했다.2개의 클럭을 소유하고 있다고 가정합니다.클럭은 둘 다 정확히 같은 속도로 체크됩니다.둘 다 정확히 동시에 표시되도록 동기화합니다.이제 두 개의 시계가 분리되어 하나의 시계가 다른 시계를 향해 일정한 속도로 이동하는 빠른 열차에 올라갑니다.뉴턴에 따르면, 이 두 시계는 여전히 같은 속도로 똑딱거리고 둘 다 같은 시간을 보여줄 것이다.뉴턴은 한 기준 프레임에서 측정된 시간의 속도는 다른 기준 프레임에서 측정된 시간의 속도와 같아야 한다고 말합니다.즉, "범용" 시간이 존재하며 다른 모든 기준 프레임의 모든 시간은 위치와 속도에 관계없이 이 표준 시간과 동일한 속도로 실행됩니다.이 시간과 동시성의 개념은 아인슈타인에 의해 나중에 그의 특수 상대성 이론(1905)에서 일반화되었는데, 그는 물리 법칙의 보편성과 그 표현의 경제성에 기초한 관성 기준 프레임 사이의 변환을 개발했다.

관성 기준 프레임의 정의는 또한 3차원 유클리드 공간을 넘어 확장될 수 있다.뉴턴은 유클리드 공간을 가정했지만 일반 상대성이론은 더 일반적인 기하학을 사용합니다.이것이 중요한 이유의 예로서 타원체의 형상을 생각해 봅시다.이 기하학에서 "자유" 입자는 정지 상태이거나 지오데식 경로를 일정한 속도로 이동하는 입자로 정의됩니다.두 개의 자유 입자는 표면의 같은 지점에서 시작하여 동일한 일정한 속도로 다른 방향으로 이동할 수 있습니다.시간이 흐른 후, 두 입자는 타원체의 반대편에서 충돌합니다.두 "자유" 입자는 일정한 속도로 이동했고, 어떠한 힘도 작용하지 않는다는 정의를 만족시켰다.가속이 일어나지 않았고, 그래서 뉴턴의 제1법칙은 옳았다.이것은 입자들이 관성 기준 프레임에 있었다는 것을 의미한다.힘이 작용하지 않았기 때문에, 두 입자가 다시 만나게 된 것은 상황의 기하학이었다.비슷한 방법으로, 이제 우리가 시공간으로 알려진 4차원 기하학에서 존재한다고 설명하는^[54] 것이 일반적입니다.이 그림에서, 이 4D 공간의 곡률은 힘이 작용하지 않더라도 질량을 가진 두 물체가 서로 끌어당기는 방식에 책임이 있다.이 시공간 곡률은 뉴턴 역학과 특수 상대성 이론에서 중력으로 알려진 힘을 대체한다.

비삽입 프레임

여기서는 관성 및 비관성 관찰 기준 프레임 간의 관계를 고려한다.이들 프레임의 기본적인 차이는 다음과 같이 가상적인 힘에 대한 비관성 프레임의 필요성입니다.

가속된 기준 프레임은 종종 "primed" 프레임으로 정의되며, 해당 프레임에 의존하는 모든 변수는 소수(예: x′, y′, a′)로 표기됩니다.

관성 기준 프레임의 원점에서 가속 기준 프레임의 원점까지의 벡터는 일반적으로 R로 표기된다.양쪽 프레임에 존재하는 관심점이 주어지면 관성 원점에서 점까지의 벡터는 r, 가속 원점에서 점까지의 벡터는 rθ라고 합니다.상황의 기하학적 구조에서 우리는

${\displaystyle \mathbf {r} =\mathbf {R} +\mathbf {r} ' .}$

시간과 관련하여 이것의 첫 번째와 두 번째 파생물을 취하면, 우리는 다음을 얻는다.

$\displaystyle \mathbf {v} = \mathbf {V} + \mathbf {v} ' , }$

${\displaystyle \mathbf {a} =\mathbf {A} +\mathbf {a} ' .}$

여기서 V와 A는 관성 시스템에 대한 가속 시스템의 속도와 가속도이고 v와 a는 관성 프레임에 대한 관심 지점의 속도와 가속도이다.

이 방정식은 두 좌표계 사이의 변환을 가능하게 한다; 예를 들어, 우리는 이제 뉴턴의 제2법칙을 다음과 같이 쓸 수 있다.

${\displaystyle \mathbf {F} =m\mathbf {a} =m\mathbf {A} +m\mathbf {a} ' .}$

가해지는 힘에 의해 가속되는 운동이 있을 때 관성의 징후가 나타납니다.감속 시 배터리 시스템을 충전하도록 설계된 전기 자동차가 제동으로 전환되면 배터리가 충전되어 관성 현상의 물리적 강도를 보여줍니다.그러나 관성의 징후는 가속(또는 감속)을 방지하지 않는다. 관성의 징후는 힘에 의한 속도 변화에 반응하여 발생하기 때문이다.기준의 회전 프레임의 관점에서 볼 때 관성의 표현은 힘을 가하는 것으로 보인다(원심 방향 또는 물체의 움직임과 직교하는 방향, 코리올리 효과).

일반적인 가속 기준 프레임의 종류는 회전 및 번역 가능한 프레임입니다(예를 들어 플레이어를 운반하는 동안 재생되는 CD에 부착된 기준 프레임).이 배열은 다음 방정식으로 이어진다(파생에 대한 가상의 힘 참조).

$\displaystyle \mathbf {a} = \mathbf {a} '+{\dot {\boldsymbol {\mega }} \times \mathbf {r} '+{\boldsymbol {v}} \times \mathbf {a} {\times}$

가속 프레임의 가속도를 해결하려면

$\displaystyle \mathbf {a} '=\mathbf {a} - {\dot {\boldsymbol {r} \times \mathbf {r} \times \mathbf {v} \times\times \mathbol {a} - {\mathbf} - {r}}$

m의 질량을 곱하면 다음과 같이 된다.

${\displaystyle \mathbf {F} '=\mathbf {F}'+\mathbf {F}'_{\mathbrm {Uler}'+\mathbf {F}+\mathbf {F}'_{F}+\mathbf {F} {F}'{\mathbf {F}'{F}'{F}'{F}'}'\petcental}$

어디에

${\displaystyle {}_{\mathrm{}}^{}}$ ${\displaystyle {\mathrm{E}}_{}^{}}$ ${\displaystyle {\mathrm{u}}_{}^{}}$ r ${\displaystyle =}$ - ${\displaystyle m}$ ${\displaystyle \omega \stackrel{}{\mathit{}}}$ ${\displaystyle \times }$ × ${\displaystyle {\mathbf{}}^{}}$ { $displaystyle$\ $mathbf${ $F }$ ' $_${ \ $mathrm${$Eler$} = - m${\ dot$\ $boldsymbol$ { } \$times$\ $mathbf { r$} ' （$$ Uler force ） ,

$F$ ${\displaystyle {\mathrm{C}}_{}^{}}$ ${\displaystyle {\mathrm{o}}_{}^{}}$ ${\displaystyle {\mathrm{l}}_{}^{}}$ ${\displaystyle {\mathrm{i}}_{}^{}}$ ${\displaystyle {\mathrm{s}}_{}^{}}$ ${\displaystyle {\prime }_{}^{}}$ ${\displaystyle =}$ - ${\displaystyle 2}$ ${\displaystyle {\mathbf{}}^{}}$× × v $′$ { $displaystyle$\ $mathbf${ $F }$ ' $_${ \ $mathrm${ $Coriolis$ } = - 2 m bold $bold$ symbol { }$}$ \ $times$ \$mathbf${ v$$}$$ ' （$$Coriolis force ） ,

$F$ c ${\displaystyle {\mathrm{n}}_{}^{}}$ ${\displaystyle {\mathrm{t}}_{}^{}}$ ${\displaystyle {\mathrm{r}}_{}^{}}$ ${\displaystyle {\mathrm{i}}_{}^{}}$ ${\displaystyle {\mathrm{u}}_{}^{}}$ ${\displaystyle {\mathrm{g}}_{}^{}}$ a ${\displaystyle l=}$ - m ${\displaystyle omega\mathit{}}$× (${\displaystyle {\mathbf{}}^{}}$ × r${\displaystyle (}$ ) ${\displaystyle =}$ ${\displaystyle m}$ ( ${\displaystyle {omega\mathrm{}}^{}}$ ${\displaystyle {}^{}{\mathbf{}}^{}}$ r${\displaystyle }$omega -${\displaystyle }$(${\displaystyle {\mathbf{}}^{}}$ r$$ )$$、 \ $displaystyle$\ $mathbf${ $F$} ' $_${ \ $mathboldsymbol${ F }$=$ - $modembold }$ ( ）원심력).

관성 기준 프레임에서 비관성 기준 프레임 분리

이론.

관성 기준 프레임과 비관성 기준 프레임은 간단히 ^[9][10]설명한 바와 같이 가상의 힘의 부재 또는 존재로 구분할 수 있다.

이것이 비관성 프레임에 있는 효과는 관찰자가 자신의 계산에 가상의 힘을 도입하도록 요구하는 것입니다.

--

가상 힘의 존재는 물리적 법칙이 사용 가능한 가장 단순한 법칙이 아님을 나타내므로 특수 상대성 원리의 관점에서 가상 힘이 존재하는 프레임은 관성 ^[55]프레임이 아니다.

비관성계의 운동 방정식은 관성력이라고 불리는 추가 항에 의해 관성계의 방정식과 다릅니다.이를 통해 시스템의 비관성 특성을 실험적으로 검출할 수 있습니다.

--

비관성 기준 프레임의 물체는 이른바 가공의 힘(의사 힘)의 영향을 받는다. 즉, 기준 프레임 자체의 가속에서 발생하는 힘이지 신체에 작용하는 물리적 힘에서 발생하는 힘은 아니다.가상의 힘의 예로는 회전 기준 프레임의 원심력과 코리올리력이 있습니다.

그렇다면, "가짜" 힘은 어떻게 "실제" 힘과 분리될 수 있을까?이 분리 없이 관성 프레임에 대한 뉴턴의 정의를 적용하는 것은 어렵다.예를 들어 관성 프레임에 고정된 물체를 생각해 보겠습니다.정지 상태에서는, 순방향의 힘이 가해지지 않습니다.그러나 고정된 축을 중심으로 회전하는 프레임에서는 물체가 원을 그리며 움직이는 것처럼 보이며 구심력(코리올리 힘과 원심력으로 구성됨)을 받는다.회전 프레임이 비관성 프레임이라고 판단하려면 어떻게 해야 합니까?이 해결 방법에는 두 가지 방법이 있습니다. 한 가지 방법은 가상의 힘(코리올리 힘과 원심력)의 원점을 찾는 것입니다.우리는 이러한 힘의 원천도, 관련 포스 캐리어도,^[56] 발생원체도 없다는 것을 알게 될 것이다.두 번째 접근법은 다양한 참조 프레임을 살펴보는 것입니다.모든 관성 프레임에 대해 코리올리 힘과 원심력이 사라지기 때문에 특수상대성 원리를 적용하면 힘이 동일하고 가장 단순한 물리 법칙을 공유하는 프레임이 사라지기 때문에 회전 프레임이 관성 프레임이 아니라고 판단할 수 있습니다.

뉴턴은 그림 2와 그림 3과 같이 회전하는 구를 사용하여 이 문제를 직접 조사했습니다.그는 구가 회전하지 않으면 모든 ^[57]기준 프레임에서 끈의 장력이 0으로 측정된다고 지적했다.구체가 회전하는 것처럼 보이는 경우(즉, 회전하는 프레임에서 정지된 구체를 관찰하는 경우), 구심력은 원심력과 코리올리의 힘에 의해 공급되므로 장력이 필요하지 않습니다.만약 구체가 정말로 회전하고 있다면, 관측된 장력은 정확히 원운동에 의해 요구되는 구심력이다.따라서 끈의 장력 측정은 관성 프레임을 식별합니다. 끈의 장력이 그 프레임에서 관찰된 것처럼 동작에 의해 요구되는 구심력을 정확하게 제공하는 것이며 다른 값은 아닙니다.즉, 관성 프레임은 가상의 힘이 사라지는 프레임입니다.

회전으로 인한 가공의 힘은 이제 그만이다.그러나 선형 가속의 경우,^[41] 뉴턴은 공통적으로 유지되는 직선 가속의 탐지 불가능에 대한 생각을 표현했다.

물체가 아무리 움직여도 동등한 가속력에 의해 평행선 방향으로 움직이면 마치 그런 힘이 없는 것처럼 그들끼리 계속 움직이게 될 것이다.

--

이 원리는 관성 프레임의 개념을 일반화한다.예를 들어, 자유낙하 리프트에 갇힌 관찰자는 리프트 외부의 어떤 것에 대한 지식이 없는 한 중력 하에서 가속하더라도 자신이 유효한 관성 프레임이라고 단언할 것이다.그래서 엄밀히 말하면 관성 프레임은 상대적인 개념입니다.이를 염두에 두고 관성 프레임을 서로 정지해 있거나 일정한 속도로 움직이는 프레임 세트로 집합적으로 정의할 수 있으므로 단일 관성 프레임을 이 세트의 요소로 정의할 수 있습니다.

이러한 아이디어를 적용하기 위해서는 프레임 내에서 관찰되는 모든 것이 프레임 자체에 의해 공유되는 베이스라인 공통 가속의 대상이 되어야 합니다.예를 들어 모든 물체가 동일한 중력 가속을 받고 엘리베이터 자체가 동일한 속도로 가속하는 엘리베이터의 예에 해당됩니다.

적용들

관성 항법 시스템은 자이로스코프와 가속도계 클러스터를 사용하여 관성 공간에 상대적인 가속도를 판단했습니다.자이로스코프가 관성공간에서 특정 방향으로 회전한 후, 각운동량 보존의 법칙은 ^{[58]: 59} 외력이 가해지는 한 그 방향을 유지하도록 요구한다.3개의 직교 자이로스코프가 관성 기준 프레임을 설정하고 가속기는 해당 프레임에 대한 가속도를 측정합니다.그런 다음 가속도를 시계와 함께 사용하여 위치 변화를 계산할 수 있습니다.따라서 관성 항법은 외부 입력이 필요하지 않으므로 외부 또는 내부 신호 ^[59]소스에 의해 방해될 수 없습니다.

항해 선박의 항해에 사용되는 자이로 나침반은 기하학적인 북쪽을 찾습니다.그것은 지구의 자기장을 감지하는 것이 아니라 관성 공간을 기준으로 하여 그렇게 한다.자이로 나침반 장치의 외부 케이스는 로컬 수직 라인과 정렬된 상태로 유지됩니다.자이로 나침반 장치 내부의 자이로스코프 휠이 회전할 때 자이로스코프 휠이 매달려 있는 방식으로 자이로스코프 휠이 회전하는 축을 지구의 축과 점차 정렬하게 됩니다.지구 축과의 정렬은 자이로스코프의 회전 축이 지구에 대해 정지하고 관성 공간에 대해 방향을 변경할 필요가 없는 유일한 방향이다.회전 후, 자이로 나침반은 불과 ^[60]15분 안에 지구의 축과 일직선 방향에 도달할 수 있다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

• 에드윈 F. Taylor and John Archibald Wheeler, 시공간 물리학, 제2판 (Freeman, NY, 1992년)
• 알버트 아인슈타인, 상대성 이론, 특수 이론과 일반 이론, 제15회(1954년)
• Poincaré, Henri (1900). "La théorie de Lorentz et le Principe de Réaction". Archives Neerlandaises. V: 253–78.
• 알버트 아인슈타인, 움직이는 물체의 전기역학, 상대성 원리에 포함, 38페이지.도버 1923

우주의 회전

• Julian B. Barbour; Herbert Pfister (1998). Mach's Principle: From Newton's Bucket to Quantum Gravity. Birkhäuser. p. 445. ISBN 0-8176-3823-7.
• PJ Nahin (1999). Time Machines. Springer. p. 369; Footnote 12. ISBN 0-387-98571-9.
• B Ciobanu, I Radinchi 회전하는 우주 ROM에서 전기장과 자기장을 모델링합니다.저널, 물리, 제53권, 제1-2호, 페이지 405-415, 부카레스트, 2008
• 유리 N. 오부호프, 토랄프 크로복, 마이크 셔프너 전단 프리 회전 팽창 물리개정 D 66, 043518 (2002) [5페이지]
• 유리 N. 오부호프 우주회전의 물리적 기초와 관찰 효과에 대하여(2000년)
• Li-Xin Li 우주 전지구 회전이 은하 일반 상대성 및 중력 형성에 미치는 영향, 30 doi:10.1023/A:1018867011142
• P 자작나무 우주는 돌고 있을까?네이처 298, 451 – 454 (1982년 7월 29일)
• Kurt^{[permanent dead link]} Gödel 아인슈타인의 중력장 방정식의 새로운 형태의 우주론적 해법의 예. Mod.물리, 제21권, 페이지 447, 1949년

외부 링크

• 스탠퍼드 철학 백과사전 엔트리
• 관성 프레임과 회전 기준 프레임 양쪽에서 보는 장면을 보여주는 YouTube의 애니메이션 클립으로 코리올리와 원심력을 시각화합니다.
• "Is Gravity An Illusion?". PBS Space Time. 3 June 2015. Archived from the original on 13 November 2021 – via YouTube.