파인만 도표
Feynman diagram이론 물리학에서 파인만 다이어그램은 아원자 입자의 행동과 상호작용을 설명하는 수학 표현식의 그림이다.이 계획은 1948년에 이 도표를 도입한 미국의 물리학자 리처드 파인만의 이름을 따서 지어졌다.아원자 입자의 상호작용은 복잡하고 이해하기 어려울 수 있다; 파인만 다이어그램은 그렇지 않으면 난해하고 추상적인 공식에 대한 간단한 시각화를 제공한다.David Kaiser에 따르면, "20세기 중반 이후 이론 물리학자들은 비판적인 계산을 할 수 있도록 돕기 위해 점점 더 이 도구로 눈을 돌리고 있습니다.파인만 다이어그램은 이론 [1]물리학의 거의 모든 측면에 혁명을 가져왔다."다이어그램은 주로 양자장 이론에 적용되지만, 고체 이론과 같은 다른 분야에서도 사용될 수 있습니다.프랭크 윌체크는 2004년 노벨 물리학상을 받은 계산은 "[윌체크]의 계산으로 힉스 [2]입자의 생산과 관찰을 위한 경로를 확립한 것처럼 파인만 도표가 없었다면 말 그대로 상상조차 할 수 없었을 것"이라고 썼다.
파인만은 양전자에 대한 에른스트 슈테켈베르크의 해석을 마치 시간을 [3]거슬러 이동하는 전자처럼 이용했다.따라서 반입자는 파인만 다이어그램에서 시간축을 따라 뒤로 이동하는 것으로 표현된다.
이론 입자 물리학에서 확률 진폭의 계산은 많은 변수에 대해 다소 크고 복잡한 적분을 사용해야 합니다.파인만 다이어그램은 이러한 적분을 그래픽으로 나타낼 수 있습니다.
파인만 다이어그램은 양자역학적 또는 통계적 장 이론의 전이 진폭 또는 상관 함수에 대한 섭동적 기여를 그래픽으로 표현한 것입니다.양자장 이론의 표준 공식에서 파인만 다이어그램은 섭동 S 행렬의 윅 확장 항을 나타냅니다.양자장 이론의 경로 적분 공식은 입자 또는 필드 중 하나의 관점에서 최초에서 최종 상태에 이르는 시스템의 가능한 모든 이력의 가중치 합으로서 전이 진폭을 나타낸다.그런 다음 전이 진폭은 양자 시스템의 초기 상태와 최종 상태 사이에 S 매트릭스의 매트릭스 요소로 주어진다.
| 양자장론 |
|---|
 |
| 역사 |
동기 및 이력
입자 물리학에서 산란 단면을 계산할 때, 입자 사이의 상호작용은 들어오는 입자와 나가는 입자를 설명하는 자유 장에서 시작하여 입자들이 서로 어떻게 편향되는지를 설명하는 상호작용 해밀턴을 포함시킴으로써 설명할 수 있습니다.산란을 위한 진폭은 모든 가능한 중간 입자 상태에 걸친 각각의 가능한 상호작용 이력의 합계입니다.해밀턴의 상호작용 횟수는 섭동 팽창의 순서이며, 장에 대한 시간 의존적인 섭동 이론은 다이슨 시리즈로 알려져 있습니다.중간 시간의 중간 상태가 에너지 고유 상태일 때(확실한 운동량을 가진 입자의 집합) 시리즈는 구식 섭동 이론(또는 시간 종속/시간 순서 섭동 이론)이라고 불립니다.
다이슨 시리즈는 파인만 다이어그램의 합계로 다시 작성할 수 있으며, 각 정점에서 에너지와 운동량이 모두 보존되지만 에너지-모멘텀 4벡터의 길이가 질량과 같을 필요는 없습니다. 즉, 중간 입자를 오프셸이라고 합니다.파인만 도표는 "구식" 용어보다 훨씬 더 쉽게 추적할 수 있습니다. 구식 방식은 입자와 반입자의 기여도를 분리하여 취급하기 때문입니다.각 파인만 다이어그램은 기하급수적으로 많은 구식 용어들의 합입니다. 각 내부 선은 입자 또는 반입자를 개별적으로 나타낼 수 있기 때문입니다.비상대론적 이론에서는 반입자가 없고 이중화도 없기 때문에 각 파인만 다이어그램은 하나의 항만 포함합니다.
파인만은 라그랑지안 장 이론에서 주어진 다이어그램에 대한 진폭을 계산하는 처방전을 주었다.각 내부 선은 가상 입자의 전파 인자에 대응합니다. 선이 만나는 각 정점은 라그랑지안의 상호작용 항에서 파생된 인자를 제공하며, 들어오는 선과 나가는 선은 에너지, 운동량 및 스핀을 전달합니다.
파인만 다이어그램은 수학적 도구로서의 가치 외에도 입자 상호작용의 본질에 대한 깊은 물리적 통찰력을 제공합니다.입자는 가능한 모든 방식으로 상호작용합니다. 사실 중간 가상 입자는 빛보다 더 빨리 전파될 수 있습니다.각 최종 상태의 확률은 그러한 모든 가능성을 합산하여 구한다.이것은 파인만이 발명한 양자 역학의 기능 적분 공식과 밀접하게 관련되어 있습니다. 경로 적분 공식 참조.
단거리 입자 상호작용에는 입자 자기 상호작용을 포함하는 신중한 제한 절차가 필요하기 때문에 그러한 계산의 순진한 적용은 종종 진폭이 무한인 다이어그램을 생성한다.에른스트 슈테켈베르크와 한스 베테가 제안하고 다이슨, 파인만, 슈윙거, 토모나가 등이 시행한 재규격화 기술은 이 효과를 보완해 골치 아픈 무한을 제거한다.정규화 후 파인만 다이어그램을 사용한 계산은 매우 높은 정확도로 실험 결과와 일치합니다.
파인만 다이어그램과 경로 적분 방법은 통계 역학에도 사용되며 고전 [4]역학에도 적용될 수 있습니다.
대체 이름
머레이 겔만은 수년 전에 비슷한 표기법을 고안한 스위스 물리학자 에른스트 슈테켈베르크의 이름을 따 파인만 도표를 항상 슈테켈베르크 도표로 언급했습니다.Stueckelberg는 양자장 이론을 위한 명백한 공변 형식주의의 필요성에 의해 동기 부여되었지만, 대칭 인자와 루프를 다루는 자동화된 방법을 제공하지는 않았다. 비록 그가 경로 적분 [5]없이 시간 입자 경로의 전방 및 후방 측면에서 올바른 물리적 해석을 최초로 발견하기는 했지만.
역사적으로, 공변 섭동 이론의 기록 장치로서, 그래프는 도입되었을 때 경로 적분이 낯설었기 때문에 파인만-다이슨 도표 또는 다이슨 [6]도표로 불렸고, 프리먼 다이슨의 구식 섭동 이론으로부터의 파생은 초기 [a]방법에 대해 훈련을 받은 물리학자들에게 더 쉽게 따라할 수 있었다.파인만은 이 도표를 위해 열심히 로비를 해야 했고, 이것은 방정식과 [7]그래프에 대해 훈련받은 기성 물리학자들을 혼란스럽게 했다.
물리적 현실의 표현
입자물리학의 관점에서 쓰여진 기본 [8][9]상호작용에 대한 그들의 발표에서, Gerard 't Hooft와 Martinus Veltman은 기본 입자의 양자 산란 물리학에 대한 우리의 현재 지식의 가장 간결한 표현으로 원래의 비정규화된 파인만 도표를 가져가기 위한 좋은 논거를 제시했습니다.그들의 동기는 James Daniel Bjorken과 Sidney Drell의 [10]신념과 일치합니다.
파인만 그래프와 계산 규칙은 양자장 이론을 이해하고 싶은 실험 숫자와 밀접하게 접촉하는 형태로 요약한다.그래프에 관한 이론의 진술이 섭동 이론을 의미할 수 있지만, 다체 문제에서의 그래픽 방법의 사용은 이 형식주의가 비거동적 성격의 현상을 다루기에 충분히 유연하다는 것을 보여준다.파인만 계산규칙의 일부 수정은 국소 표준 양자장 이론의 정교한 수학적 구조보다 훨씬 오래 지속될 수 있다.
현재 반대 의견은 없다.양자장 이론에서 파인만 다이어그램은 라그랑지안으로부터 파인만 규칙에 의해 얻어진다.
치수정규화는 파인만 다이어그램의 평가에서 적분을 정규화하는 방법으로, 차원이라고 불리는 보조복소 파라미터 d의 meromaphic 함수인 값을 할당합니다.치수 정규화는 시공간 치수 d 및 시공간 점에 따라 파인만 적분을 적분으로 쓴다.
입자 경로 해석
파인만 다이어그램은 입자 상호작용의 관점에서 양자장 이론 과정을 표현한 것입니다.입자는 입자의 종류에 따라 화살표로 나타내거나 없이 꼬불꼬불하거나 직선으로 나타낼 수 있습니다.선이 다른 선과 연결되는 점은 정점이며, 여기서 새로운 입자를 방출하거나 흡수하거나 서로 방향을 바꾸거나 유형을 변경함으로써 입자가 만나 상호작용합니다.
라인에는 세 가지 유형이 있습니다.내부 라인은 두 개의 정점을 연결하고, 들어오는 라인은 "과거"에서 정점으로 확장되어 초기 상태를 나타내며, 나가는 라인은 정점에서 "미래"로 확장되어 최종 상태를 나타냅니다(후자 2개는 외부 라인이라고도 합니다).전통적으로 그림의 맨 아래는 과거, 맨 위는 미래입니다.다른 때는 과거가 왼쪽, 미래가 오른쪽입니다.산란 진폭 대신 상관 함수를 계산할 때 과거와 미래가 없으며 모든 라인이 내부입니다.그리고 입자는 작은 x에서 시작되어 상관관계가 계산되는 연산자의 위치를 나타냅니다.
파인만 다이어그램은 여러 가지 다른 방식으로 발생할 수 있는 공정의 총 진폭에 대한 기여도를 그림으로 나타낸 것입니다.들어오는 입자의 그룹이 서로 흩어지는 경우, 이 과정은 입자가 시간 역행 경로를 포함하여 가능한 모든 경로를 통과하는 것으로 간주할 수 있습니다.
파인만 다이어그램은 모두 입자 산란을 묘사하기 때문에 종종 시공간 다이어그램 및 버블 챔버 이미지와 혼동됩니다.파인만 다이어그램은 산란 과정 중 입자의 물리적 위치가 아닌 입자의 상호작용을 나타내는 그래프입니다.버블 챔버 그림과 달리 파인만 다이어그램의 합만이 주어진 입자 상호작용을 나타냅니다. 입자는 상호작용할 때마다 특정 다이어그램을 선택하지 않습니다.합계의 법칙은 중첩의 원리와 일치합니다. 즉, 모든 다이어그램은 프로세스의 총 진폭에 기여합니다.
묘사
파인만 다이어그램은 초기 양자 상태에서 최종 양자 상태로의 양자 전이 진폭에 대한 섭동적 기여를 나타낸다.
예를 들어 전자-양전자 소멸 과정에서 초기 상태는 전자 1개와 양전자 1개로 최종 상태는 광자 2개입니다.
초기 상태는 다이어그램의 왼쪽에 있고 최종 상태는 오른쪽에 있다고 가정하는 경우가 많습니다(다른 규칙도 자주 사용되지만).
파인만 다이어그램은 정점이라고 하는 점과 정점에 부착된 선으로 구성됩니다.
초기 상태의 입자는 초기 상태의 방향으로 돌출된 선(예: 왼쪽)으로 표현되며, 최종 상태의 입자는 최종 상태의 방향으로 돌출된 선(예: 오른쪽)으로 표현됩니다.
QED에는 두 가지 유형의 입자가 있습니다: 전자 또는 양전자(페르미온이라고 함)와 교환 입자(게이지 보손이라고 합니다.파인만 다이어그램에는 다음과 같이 표시됩니다.
- 초기 상태의 전자는 실선으로 표시되며, 예를 들어 입자의 스핀을 나타내는 화살표가 정점(→•)을 가리킵니다.
- 최종 상태의 전자는 선으로 나타내며, 예를 들어 정점에서 먼 곳을 가리키는 입자의 스핀을 나타내는 화살표가 있다:(•→).
- 초기 상태의 양전자는 실선으로 표시되며, 예를 들어 정점에서 먼 곳을 가리키는 입자의 스핀을 나타내는 화살표가 표시됩니다. (←•)
- 최종 상태의 양전자는 예를 들어 정점을 가리키는 입자의 스핀을 나타내는 화살표가 있는 선으로 표시됩니다(•←).
- 첫 번째와 마지막 상태의 Virtual Photon은 물결선(~• 및 •~)으로 표시됩니다.
QED에서 정점은 항상 세 개의 선을 가지고 있습니다. 하나는 정점으로 향하는 화살표가 있는 페르미온 선이고 다른 하나는 정점에서 떨어진 화살표가 있는 페르미온 선입니다.
정점은 보손 전파기 또는 페르미온 전파기로 연결될 수 있습니다.2개의 정점(•••)을 연결하는 물결선으로 보스 전파기를 나타낸다.페르미온 전파기는 두 개의 정점(•←•)을 연결하는 실선으로 표현된다.
정점 수는 전환 진폭의 섭동 직렬 확장에서 항의 순서를 제공합니다.
전자-양전자 소멸 예시
- e+ + e− → 2 인치
에는 인접한 2차 파인만 다이어그램의 영향이 있습니다.
초기 상태(하단, 초기 시간)에는 전자(e−)와 양전자(e+)가 각각 1개 있고, 최종 상태(상단, 후기 시간)에는 광자(θ)가 2개 있다.
표준 양자화 공식
양자 시스템의 초기 상태 iµ에서 최종 상태 fµ로의 전환에 대한 확률 진폭은 매트릭스 요소에 의해 주어진다.
여기서 S는 S-행렬이다.시간 진화 연산자 U의 관점에서, 그것은 단순하다.
상호 작용 그림에서 이것은 다음과 같이 확장됩니다.
여기서V H는 교호작용 Hamiltonian이고 T는 연산자의 시간 순서 곱을 나타냅니다.다이슨의 공식은 시간순서 행렬을 해밀턴 밀도의 힘으로 섭동 급수로 확장한다.
마찬가지로, 라그랑지안V L의 상호작용을 통해, 이것은
파인만 다이어그램은 S-행렬의 Dyson 시리즈의 n차 항(n) S에서 Wick의 시간 순서 제품 확장에서 단일 합계를 그래픽으로 나타낸 것입니다.
여기서 N은 연산자의 정상 순서 곱을 나타내며 (±) 페르미온 연산자를 이동시킬 때 가능한 부호 변화를 처리하여 수축(전파기)을 위해 이들을 모이게 하고, A는 가능한 모든 수축을 나타냅니다.
파인만의 법칙
그림은 라그랑지안 상호작용에 따라 파인만 규칙에 따라 그려집니다.QED 상호작용의 경우 Lagrangian
페르미온장 θ와 보손 게이지장μ A의 상호작용을 설명하는 파인만 법칙은 좌표 공간에서 다음과 같이 공식화할 수 있다.
- 각 적분 좌표j x는 점(정점이라고도 함)으로 표현된다.
- 보손 전파기는 두 점을 연결하는 꿈틀거리는 선으로 표현된다.
- 페르미온 전파기는 두 점을 연결하는 실선으로 표현된다.
- μ ( i }(는i 점 x에 부착된 꿈틀거리는 선으로 나타납니다.
- 페르미온장 δ(x)는i 점 x에i 부착된 실선으로 점을 향해 화살표가 표시된다.
- 항페르미온장θ(xi)는 점x에 부착된 실선으로 표시되며, 점x에서i 화살표가 떨어져 있다.
예: QED에서의 2차 프로세스
S 행렬의 2차 섭동 항은 다음과 같다.
페르미온 산란
Wick의 인테그랜드 확장은 (특히) 다음과 같은 조건을 제시합니다.
어디에
파인만 게이지의 전자기 수축(전파기)입니다.이 용어는 오른쪽에 있는 파인만 다이어그램으로 나타납니다.이 다이어그램은 다음 프로세스에 기여합니다.
- e−− 산란(오른쪽의 초기 상태, 다이어그램 왼쪽의 최종 상태);
- e++ 산란(왼쪽의 초기 상태, 다이어그램 오른쪽의 최종 상태);
- e−+ 산란(하단/상단의 초기 상태, 다이어그램의 상단/하단의 최종 상태).
e−+ 쌍의 콤프턴 산란 및 소멸/생성
확장의 또 다른 흥미로운 용어는
어디에
페르미온 수축(촉진제)입니다.
경로 적분 공식
경로 적분에서는 가능한 모든 필드 이력에 통합된 필드 라그랑지안은 필드 구성 간에 이동하는 확률 진폭을 정의합니다.이치에 맞도록, 필드 이론은 잘 정의된 접지 상태를 가져야 하며 적분은 약간의 가상 시간, 즉 윅 회전으로 수행되어야 한다.경로 적분 형식주의는 위의 표준 연산자 형식주의와 완전히 동등하다.
스칼라 장 라그랑지안
단순한 예로는 d차원의 자유상대론적 스칼라장이 있는데, 그 작용 적분은 다음과 같다.
프로세스의 확률 진폭은 다음과 같습니다.
여기서 A와 B는 경계 조건을 정의하는 공간과 같은 하이퍼서페이스입니다.시작 하이퍼서페이스 상의 모든 δ(A)의 수집은 점 입자의 시작 위치와 유사한 필드의 초기값을 제공하며, 최종 하이퍼서페이스의 각 지점의 필드값 δ(B)는 최종 필드값을 정의하며, 최종 필드값은 변동할 수 있으므로 서로 다른 진폭이 서로 다른 값으로 끝납니다.필드 대 필드 전환 진폭입니다.
경로 적분은 초기 상태와 최종 상태 사이의 연산자의 기대값을 제공합니다.
그리고 A와 B가 무한한 과거와 무한한 미래로 후퇴하는 한계에서 중요한 유일한 기여는 지면 상태(이는 경로 적분이 가상 시간으로 약간 회전하는 경우에만 엄격하게 해당)이다.경로 적분은 확률 분포와 유사한 것으로 간주할 수 있으며, 상수를 곱해도 아무것도 변경되지 않도록 정의하는 것이 편리합니다.
맨 아래에 있는 정규화 계수는 필드의 분할 함수라고 하며, 가상 시간으로 회전할 때 0 온도에서 통계 기계 분할 함수와 일치합니다.
초기에서 최종까지의 진폭은 필드의 변동이 무한해질 수 있기 때문에 처음부터 연속체 한계를 생각하면 잘못 정의됩니다.따라서 경로 계산은 격자 간격 a를 갖는 이산 사각 격자에 있다고 생각할 수 있으며 한계 a → 0을 신중하게 취해야 한다[clarification needed].최종 결과가 격자의 모양이나 a의 값에 의존하지 않으면 연속체 한계가 존재합니다.
격자 위에
격자(i)에서 필드를 푸리에 모드로 확장할 수 있습니다.
여기에 통합 도메인 k에 변의 길이.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{입방체로 제한된다.디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}2π/a, k의 큰 값이 허용되지 않다.k 측정에는 푸리에 변환의 2µ 인수가 포함되어 있다는 점에 유의해야 합니다. 이는 QFT의 k-적분에 대한 최선의 표준 규칙입니다.격자는 큰 k의 변동은 즉시 기여하는 것이 허용되지 않고 한계 a → 0에서 기여하기 시작함을 의미합니다. 때로는 격자 대신 필드 모드가 높은 k 값에서 끊어집니다.
또한 시공간 부피가 유한하다고 간주하는 것이 때때로 편리하므로 k 모드도 격자가 된다.이는 k의 상호작용이 국소화되지 않기 때문에 공간 적재 한계만큼 엄격히 필요한 것은 아니지만 k-적분 앞의 요인 및 발생하는 운동량 보존 델타 함수를 추적하는 데 편리하다.
격자에서 (ii) 작용은 이산화되어야 한다.
여기서 "x,y"는 가장 가까운 격자 인접 x와 y의 쌍입니다.이산화는 도함수 「」μ의 의미를 정의하는 것으로 생각할 필요가 있습니다.
격자 푸리에 모드의 경우 다음과 같이 동작을 기록할 수 있습니다.
k가 0에 가까운 경우, 이것은 다음과 같다.
이제 우리는 원래의 동작의 연속체 푸리에 변환이 있습니다.유한 부피에서 dk의d 양은 극소량이 아니라 인접한 푸리에 모드에 의해 만들어지는 상자의 부피, 즉 (2µ/d
V)가 된다.
필드 θ는 실제 값이기 때문에 푸리에 변환은 다음 조건을 따릅니다.
실수부 및 허수부에서는 θ(k)의 실수부는 k의 짝수함수이며, 허수부는 홀수함수이다.푸리에 변환은 이중 카운트를 방지하므로 다음과 같이 쓸 수 있습니다.
각 쌍(k,-k)에 대해 정확히 한 번 통합되는 통합 도메인에 대해 설명합니다.
작업이 포함된 복잡한 스칼라 필드의 경우
푸리에 변환은 구속되지 않습니다.
적분은 전체 k 위에 있습니다.
δ(x)의 모든 다른 값에 적분하는 것은 모든 푸리에 모드에 적분하는 것과 같습니다. 푸리에 변환을 취하는 것은 필드 좌표의 단일 선형 변환이기 때문입니다.선형 변환을 통해 다차원 적분의 좌표를 변경하면 변환 행렬의 행렬식에 의해 새 적분의 값이 지정됩니다.한다면
그리고나서
A가 회전일 경우
따라서 det A = ±1 이며, 부호는 회전에 반사가 포함되는지 여부에 따라 달라진다.
좌표를 θ(x)에서 θ(k)로 변경하는 행렬은 푸리에 변환의 정의에서 읽을 수 있습니다.
푸리에 반전 정리는 다음과 같은 역수를 알려 줍니다.
복소공역-포도당이고, 최대 2µ의 인수입니다.유한 체적 격자에서 행렬식은 0이 아니며 필드 값과 독립적입니다.
경로 적분은 k의 각 값에서 별도의 계수이다.
인자d dk는 정사각형 격자 상자에서 k-공간에서 이산 셀의 극소 부피이다.
여기서 L은 상자의 측면 길이입니다.각 개별 인자는 진동 가우스이며, 볼륨이 무한대로 이동함에 따라 가우스 폭이 분산됩니다.
상상의 시간에서 유클리드 작용은 양의 정이 되며, 확률 분포로 해석될 수 있다.값이 θ인k 필드의 확률은 다음과 같습니다.
필드의 기대치는 확률 분포에 따라 선택되었을 때 필드의 통계 기대치입니다.
θ의k 확률은 곱이므로 k의 각 분리값에서 θ의k 값은 독립적으로 가우스 분포된다.가우스의 분산은 1/kdk이며2d, 이는 형식적으로는 무한하지만 무한 볼륨에서 변동이 제한되지 않음을 의미합니다.임의의 유한 부피에서 적분은 이산합으로 치환되며 적분의 분산은 V/k이다2.
몬테카를로
경로 적분은 유클리드 스칼라 필드 구성을 생성하는 확률론적 알고리즘을 정의합니다.파수 k에서 각 푸리에 모드의 실수 및 허수 부분을 무작위로 선택하여 분산 1/k의2 가우스 랜덤 변수가 됩니다.이것에 의해, 설정 δC(k)가 랜덤으로 생성되어 푸리에 변환에 의해서 δC(x)가 주어집니다.실제 스칼라 필드의 경우 알고리즘은 각 쌍 "(k)", "(-k)" 중 하나만 생성하고 두 번째 쌍은 첫 번째 쌍의 복소 공역이어야 합니다.
상관함수를 찾으려면 다음 절차에 따라 필드를 여러 번 생성하고 통계 평균을 구하십시오.
여기서 C는 Configuration의 수, 합계는 각 Configuration의 필드 값 곱입니다.유클리드 상관함수는 통계학이나 통계역학에서의 상관함수와 동일하다.양자역학적 상관함수는 유클리드 상관함수의 분석적 연속이다.
2차 작용이 있는 자유장의 경우 확률 분포는 고차원 가우스이며 통계 평균은 명시적 공식에 의해 주어진다.그러나 몬테카를로 방법은 상관함수에 대한 닫힌 형식이 없는 보손 상호작용 장 이론에도 잘 적용된다.
스칼라 전파기
각 모드는 독립적으로 가우스 분포를 따릅니다.필드 모드의 예상값은 쉽게 계산할 수 있습니다.
k † kµ의 경우, 그 이후 두 가우스 랜덤 변수는 독립적이며 둘 다 평균이 0입니다.
두 k-값이 일치할 때, 이것은 가우스 분산이기 때문에 유한 체적 V에서.무한 볼륨 제한에서는
엄밀히 말하면, 이것은 근사치입니다.격자 전파기는 다음과 같습니다.
그러나 k = 0 근처에서는 격자 간격에 비해 장 변동이 긴 경우 두 형태가 일치합니다.
델타 함수는 k 적분 측정에서 2µ 인자를 상쇄하기 위해 2µ 인자를 포함한다는 점을 강조하는 것이 중요합니다.
여기서 θD(k)는 일반적인 1차원 디랙 델타 함수이다.델타 함수에 대한 이 규칙은 보편적이지 않다. 일부 저자는 델타 함수(및 k-적분)에서 2µ의 계수를 명시적으로 유지한다.
운동 방정식
전파기의 형태는 필드의 운동 방정식을 사용하면 더 쉽게 찾을 수 있습니다.라그랑지안으로부터 운동방정식은 다음과 같다.
기대치에는 다음과 같은 내용이 있습니다.
여기서 도함수는 x에 작용하며, 동일성은 x와 y가 일치하는 경우를 제외하고 모든 곳에서 참이며 연산자의 순서가 중요합니다.특이점의 형태는 델타 함수로 표준 정류 관계에서 이해할 수 있다.정의(유클리드)파인만 전파기 δ는 시간 순서 2점 함수(경로 적분 함수에서 나오는 함수)의 푸리에 변환입니다.
그 때문에, 다음과 같이 됩니다.
만약 운동 방정식이 선형이라면, 전파자는 항상 자유 라그랑지안을 정의하는 2차 형식 행렬의 역수입니다. 왜냐하면 이것은 운동 방정식을 제공하기 때문입니다.경로 적분에서도 직접 확인할 수 있습니다.유클리드 이론에서 i의 인수는 사라진다.
윅 정리
각 필드 모드는 독립적인 가우스이므로, 많은 필드 모드의 곱에 대한 기대값은 윅의 정리를 따릅니다.
필드 모드가 쌍으로 일치하지 않는 한 제로입니다.즉, 홀수인 θ에 대해서는 0, 짝수인 θ에 대해서는 델타 함수를 사용하여 각 쌍의 기여와 같습니다.
여기서 합계는 필드 모드의 각 파티션 위에 쌍으로 표시되고 곱은 쌍 위에 있습니다.예를들면,
Wick의 정리는 각 필드 삽입을 당글링 라인으로 생각할 수 있으며, 각 라인을 쌍으로 연결하여 쌍으로 각 파트너의 운동량이 동일함을 보증하는 델타 함수 계수를 넣고 전파기로 나누어 기대치를 산출하는 것이다.
더 높은 가우스 모멘트 - Wick의 정리를 완성합니다.
Wick의 정리가 증명되기까지는 아직 미묘한 점이 남아 있습니다. 두 개 이상의 s가 같은 모멘텀을 갖는다면 어떻게 될까요?홀수일 경우 적분은 0이 되고 음수 값은 양의 값으로 취소됩니다.단, 짝수일 경우 적분은 양수입니다.이전 데모에서는 는 쌍으로만 일치한다고 가정했습니다.
단, 이 정리는 임의의 다수의\가 동일한 경우에도 정확하며, 이는 가우스 통합의 주목할 만한 특성입니다.
I로 나누면
만약 Wick의 정리가 맞다면, 2n개의 다른 x: 목록으로 가능한 모든 쌍으로 더 높은 모멘트가 주어질 것이다.
여기서 x는 모두 같은 변수이고 지수는 단지 쌍을 이루는 방법의 수를 추적하는 것입니다.첫 번째 x는 2n - 1과 쌍을 이룰 수 있으며 2n - 2는 남습니다.다음 쌍체화되지 않은 x는 2n - 3 다른 x 2n - 4와 쌍체화할 수 있습니다.즉, Wick의 정리가 수정되지 않은 상태에서2n x의 기대값은 다음과 같아야 합니다.
사실 이게 정답이에요.그래서 윅의 정리는 내부 변수들의 모멘타가 얼마나 일치하든지 상관없이 유지된다.
상호 작용
2차 기여는 항상 가우스이기 때문에 상호작용은 고차 기여로 표현된다.가장 간단한 상호작용은 작용이 있는 4차 자기 상호작용입니다.
조합 계수 4!의 이유는 곧 밝혀질 것이다.격자(또는 연속체) 푸리에 모드로 동작 쓰기:
여기서F S는 자유 작용이며, 그 상관 함수는 윅의 정리에 의해 주어진다.경로 적분 중의 S의 지수를 θ의 거듭제곱으로 확장할 수 있으며, 자유 작용에 대한 일련의 보정을 제공한다.
상호작용 동작에 필수적인 경로는 자유 동작에 대한 수정의 거듭제곱 시리즈입니다.X로 표현되는 항은 θ(k)의 각 요인에 대해 하나씩 네 개의 반직선으로 간주해야 한다.반직선은 정점에서 만나 모멘타의 합이 모두 같도록 하는 델타 함수를 제공합니다.
상호 작용 이론에서 상관 함수를 계산하기 위해, X 항에서 기여가 있습니다.예를 들어, 4필드 콜리레이터의 패스 인테그레이터는 다음과 같습니다.
자유 필드에서는 모멘타 k가 쌍으로 같을 때만 0이 아니었고, 현재는 k의 모든 값에 대해 0이 아니다.삽입 θ(ki)의 모멘타는 확장 시 X의 모멘타와 일치할 수 있습니다.삽입물은 하프 라인으로 간주해야 합니다.이 경우 4개는 모멘텀 k를 전달하지만 1개는 통합되지 않습니다.
가장 낮은 차수의 기여는 동작의 Taylor 확장의 첫 번째 중요하지 않은 용어−SF eX에서 비롯됩니다.윅의 정리에서는 X의 반직선의 모멘타, X의 δ(k) 인자가 쌍으로 외부 반직선의 모멘타와 일치해야 한다.새로운 기여는 다음과 같습니다.
X의 하프라인을 외부 하프라인과 일치시키는 방법이 정확히 4가지이므로 X 내부의 4!는 취소됩니다.쌍으로 반선을 맞추는 이러한 다른 방법들은 k의 값에1,2,3,4 관계없이 윅의 정리에 의해 정확히 한 번 기여한다.
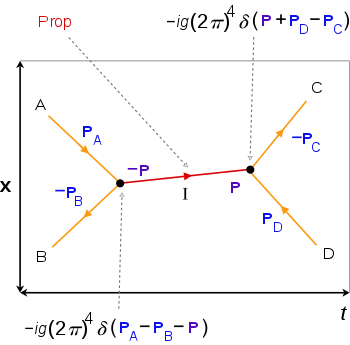
파인만 도표
X의 거듭제곱으로 작용이 확대됨에 따라 X의 수가 점차 증가하는 일련의 항이 제공됩니다.정확히 n X를 갖는 항의 기여도를 n차수라고 합니다.
n번째 주문 조건은 다음과 같습니다.
- 4n 내부 반직선, 이것은 X의 θ(k)의 계수이다.이 모든 것이 정점에서 끝나며 가능한 모든 k에 통합됩니다.
- 외부 하프라인. 이것은 적분 내의 θ(k) 삽입에서 오는 것입니다.
윅의 정리에 따르면, 각 반직선의 쌍은 선을 만들기 위해 함께 쌍이 되어야 하며, 이 선은 다음의 계수를 제공한다.
기여도가 높아집니다.즉, 선을 만드는 두 개의 하프 라인이 같은 운동량과 반대 운동량을 갖도록 강제됩니다.선 자체에 화살표로 라벨을 붙이고 선에 평행하게 그리고 k라인의 운동량으로 라벨을 붙여야 한다.화살표 끝의 하프라인은 운동량 k를 전달하고 헤드엔드의 하프라인은 운동량 k를 전달한다.두 개의 하프라인 중 하나가 외부일 경우 내부 k가 외부 k와 동일하도록 강제하기 때문에 내부 k 위의 적분이 사라집니다.둘 다 내부일 경우 k에 대한 적분은 유지됩니다.
삽입을 나타내는 X의 반직선과 외부 반직선을 연결하여 형성된 도표는 이 이론의 파인만 도표입니다.각 선은 전파기인 1/k2 계수를 전달하며 정점에서 정점으로 이동하거나 삽입으로 끝납니다.내부일 경우 통합됩니다.각 정점에서 들어오는 총 k는 나가는 총 k와 같습니다.
반직선을 선으로 결합하여 다이어그램을 만드는 방법의 수는 지수의 Taylor 계열과 각 정점의 4!에서 오는 요인 요인을 거의 완전히 상쇄합니다.
루프 순서
포레스트 다이어그램은 모든 내부 라인이 외부 라인에 의해 완전히 결정되는 모멘텀과 각 정점에서 들어오는 모멘텀과 나가는 모멘텀이 동일한 상태를 갖는 다이어그램입니다.이러한 다이어그램의 기여는 통합 없이 전파자의 산물입니다.트리 다이어그램은 연결된 포레스트 다이어그램입니다.
트리 다이어그램의 예로는 4개의 외부 라인이 각각 X로 끝나는 것을 들 수 있습니다.다른 하나는 X에서 3개의 외부선이 끝나고 나머지 반선은 다른 반선과 결합하고 이 X의 나머지 반선은 외부선으로 이어지는 것입니다.이것들은 모두 포레스트 다이어그램(모든 나무가 포레스트인 것처럼)입니다.포레스트가 아닌 예로는 8개의 외부선이 2개의 X로 끝나는 것이 있습니다.
이러한 모든 경우에, 모든 내부 라인의 모멘타는 외부 모멘타와 각 정점의 운동량 보존 조건에 의해 결정된다는 것을 쉽게 확인할 수 있다.
포레스트 다이어그램이 아닌 다이어그램은 루프 다이어그램이라고 불리며, 예를 들어 X의 두 줄은 외부 라인에 결합되고 나머지 두 줄은 서로 결합됩니다.서로 결합된 두 선은 동일한 정점으로 들어가고 나가므로 모멘텀을 가질 수 있습니다.더 복잡한 예로는 다리를 서로 연결함으로써 두 개의 X가 서로 결합되는 경우가 있습니다.이 그림에는 외선이 전혀 없습니다.
루프 다이어그램을 루프 다이어그램이라고 하는 이유는 운동량 보존에 의해 결정되지 않은 k-적분의 수가 그림에서 독립 루프가 계산되는 독립 폐쇄 루프의 수와 같기 때문입니다.호몰로지는 실제 값(실제d R 값)이며, 각 라인과 관련된 값이 모멘텀입니다.경계 연산자는 각 선을 양수 부호가 선두에 있고 음수 부호가 끝에 있는 끝 수직의 합으로 가져옵니다.운동량이 보존되는 조건은 k-값 가중 그래프의 경계가 0인 조건이다.
유효한 k 값 세트는 닫힌 루프가 있을 때마다 임의로 재정의할 수 있습니다.닫힌 루프는 인접한 정점의 순환 경로로 동일한 정점을 다시 찾지 않습니다.이러한 주기는 가상의 2세포의 경계로 생각할 수 있다.k의 재정의까지(즉, 2-셀의 경계까지) 운동량을 보존하는 그래프의 k-라벨은 그래프의 첫 번째 호몰로지를 정의한다.결정되지 않은 독립 모멘타의 수는 독립 호몰로지 루프의 수와 같습니다.많은 그래프에서 이것은 가장 직관적인 방법으로 카운트된 루프 수와 동일합니다.
대칭 계수
반선을 결합하여 주어진 파인만 다이어그램을 형성하는 방법은 많고, Wick의 정리에 따르면 반선을 조합하는 각 방법은 동등하게 기여합니다.이것은 종종 각 항의 분모에 있는 인수분석을 완전히 취소하지만, 때로는 완전하지 않은 경우도 있다.
비분모는 다이어그램의 대칭 계수라고 불립니다.상관 함수에 대한 각 다이어그램의 기여도를 대칭 인수로 나누어야 합니다.
예를 들어, 두 개의 외부 선이 하나의 X에 결합되고 나머지 두 개의 반직선이 서로 결합되어 형성된 Feyman 다이어그램이 있다고 가정합니다.외부 하프라인을 X에 결합하는 방법은 4×3가지가 있으며, 나머지 2개의 라인을 서로 결합하는 방법은 1개뿐입니다.X는 4로 나눕니다! = 4 × 3 × 2. 그러나 X 반선을 연결하여 도표를 만드는 방법은 4 × 3에 불과하므로 이 도표의 기여도는 2로 나눕니다.
다른 예로, 한 X의 모든 반직선을 다른 X의 모든 반직선에 결합하여 형성된 다이어그램을 생각해 보겠습니다.이 도표는 외부 선과 연결되어 있지 않기 때문에 진공 거품이라고 불립니다.이 도표를 구성하는 방법은 4가지가 있지만 분모에는 2!(지수의 확장으로 X가 2개 있음)와 4!의 두 개의 계수가 포함됩니다.기여는 4!/2 × 4! × 4! = 1/48을 곱한다.
또 다른 예로는 2개의 X로 이루어진 파인만 다이어그램이 있습니다.여기서 각 X는 최대 2개의 외부 선으로 연결되고 나머지 2개의 X의 반직선은 서로 결합됩니다.X를 2개의 외부 회선에 링크하는 방법의 수는 4 × 3이며, 어느 쪽이든 X가 어느 쪽 쌍에 링크할 수 있기 때문에 추가 계수는 2가 됩니다.두 X의 나머지 두 개의 반직선은 두 가지 방법으로 서로 연결될 수 있으므로, 다이어그램을 구성하는 총 방법의 수는 4 × 3 × 4 × 3 × 2 × 2인 반면, 분모는 4! × 4! × 2!이다.총 대칭 계수는 2이고 이 다이어그램의 기여도를 2로 나눕니다.
대칭 계수 정리는 일반적인 다이어그램의 대칭 계수를 제공합니다. 각 파인만 다이어그램의 기여는 자기동형성 그룹의 순서, 즉 가지고 있는 대칭의 수로 나누어야 합니다.
파인만 그래프의 자기동형성은 다음과 같은 성질을 가진 선의 순열 M과 정점의 순열 N이다.
- 라인 l이 정점 v에서 정점 v'로 이동하면 M(l)은 N(v)에서 N(v')으로 이동한다.실제 스칼라 필드의 경우와 같이 회선이 무방향일 경우 M(l)도 N(v')에서N(v)로 이동할 수 있습니다.
- 라인 l이 외부 회선으로 끝나는 경우, M(l)은 같은 외부 회선으로 끝납니다.
- 행의 종류가 다른 경우는, M(l)에 의해서 그 타입이 보관 유지됩니다.
이 정리는 입자 경로의 관점에서 해석됩니다: 동일한 입자가 존재할 때, 모든 중간 입자의 적분은 동일한 입자를 교환하는 것만으로 다른 상태를 이중으로 세어서는 안 됩니다.
증명: 이 정리를 증명하기 위해 다이어그램의 모든 내부 및 외부 선에 고유한 이름을 붙입니다.그런 다음 반선을 이름에 연결한 다음 나머지 반선을 연결하여 다이어그램을 작성합니다.
이제 명명된 다이어그램을 구성하는 방법을 세어 보십시오.X의 각 순열은 다른 패턴의 링크 이름을 하프라인에 제공합니다.이것은 n!의 인수입니다.단일 X에서 반직선의 각 순열은 4!의 계수를 제공합니다.그래서 명명된 다이어그램은 파인만 팽창의 분모만큼 다양한 방법으로 형성될 수 있습니다.
그러나 명명되지 않은 도표의 수는 그래프의 자기동형성 그룹의 순서로 명명된 도표의 수보다 적다.
연결도: 링크 클러스터 정리
대략적으로 말하면, 파인만 다이어그램은 모든 정점과 전파선이 일련의 정점과 전파선에 의해 연결되었다고 불립니다.무방향 그래프로 보는 경우 연결된 것입니다.QFT에서 이러한 다이어그램의 현저한 관련성은 양자 분할 함수 Z[J]를 결정하기에 충분하다는 사실에 기인한다.보다 정확하게는 연결된 파인만 다이어그램이 다음을 결정합니다.
이를 보려면 을 상기해야 한다.
여러 개의 연결된i 성분 C로 구성된다고 생각될 수 있는 일부(임의) 파인만 다이어그램으로 구성된 D를k 사용합니다.Feynman 다이어그램k D에서 성분i C의 복사본 n개가 발견되면 대칭 계수i n!을i 포함해야 합니다.그러나, 결국, 분할 함수에 대한 파인만k 다이어그램 D의 각 기여는 일반 형식을 가집니다.
여기서 i는 가능한 많은 연결된 Feynman 다이어그램에 라벨을 붙입니다.
D에서k Z[J]까지 그러한 공헌을 연속적으로 작성하는 스킴은 다음과 같이 취득된다.
따라서 산출된다.
정규화0 Z = exp W[0] = 1을 설정하려면 연결된 모든 진공 다이어그램, 즉 소스 J가 없는 다이어그램(파인만 다이어그램의 외부 다리라고도 함)을 계산합니다.
진공 거품
링크드 클러스터 정리의 직접적인 결과는 상관 함수를 계산할 때 외부 선이 없는 모든 진공 기포, 다이어그램이 취소된다는 것입니다.상관 함수는 경로 적분의 비율로 제공됩니다.
위는 외부 라인에 전혀 연결되지 않은 분리된 다이어그램을 포함하여 모든 파인만 다이어그램의 합입니다.연결된 다이어그램의 관점에서 분자는 분모와 동일한 진공 기포의 기여도를 포함합니다.
여기서 Sum over E 다이어그램은 각각의 연결된 구성요소가 적어도 하나의 외부 라인으로 끝나는 다이어그램만 포함합니다.진공 기포는 외부 라인에 관계없이 동일하며 전체 승수를 산출합니다.분모는 모든 진공 기포에 대한 합이며, 나눗셈은 두 번째 요인을 나눕니다.
그러면 진공 기포는 경로 적분의 정의에 따라 다음과 같은 Z 자체를 결정하는 데만 유용합니다.
여기서 δ는 진공 중의 에너지 밀도입니다.각 진공 버블은 각 정점에서 총 k를 0으로 하는 θ(k)의 계수를 포함하고, 외부 라인이 없는 경우에는 운동량 보존이 과도하게 적용되기 때문에 θ(0)의 계수를 포함한다.유한 부피에서 이 인자는 공간 시간의 총 부피로 식별될 수 있습니다.부피로 나누면 진공 버블의 나머지 일체형에는 진공의 에너지 밀도에 기여한다는 해석이 있습니다.
원천
상관 함수는 연결된 파인만 다이어그램의 합이지만 형식주의는 연결된 다이어그램과 분리된 다이어그램을 다르게 취급합니다.내부 선은 정점으로 끝나는 반면 외부 선은 삽입으로 이어집니다.소스를 도입함으로써 하나의 선이 끝날 수 있는 새로운 정점을 만들어 형식주의를 통합합니다.
소스는 외부 필드입니다.외부 필드는 액션에 기여하지만 동적 변수는 아닙니다.스칼라 필드 소스는 (로렌츠) 라그랑지안 항에 기여하는 또 다른 스칼라 필드 h입니다.
파인만 확장에서는 정점에서 하나의 반직선으로 끝나는 H 항을 제공합니다.파인만 다이어그램의 선은 이제 X 정점 또는 H 정점에서 끝날 수 있으며 한 선만 H 정점으로 들어갑니다.H 꼭지점에 대한 파인만 규칙은 운동량이 k인 H의 선이 h(k)의 인자를 얻는 것입니다.
소스 존재 시 연결된 다이어그램의 합계는 소스 부재 시 연결된 각 다이어그램에 대한 항을 포함합니다. 단, 이제 다이어그램은 소스 위에서 끝날 수 있습니다.전통적으로 소스는 작은 "×"로 표시되며, 정확히 삽입처럼 한 줄이 뻗어 있습니다.
여기서 C(k1,...kn)는 그림과 같이 운동량을 전달하는 n개의 외부 라인과 연결된 다이어그램입니다.합계는 이전과 같이 연결된 모든 다이어그램에 표시됩니다.
필드 h는 역동적이지 않습니다.즉, h를 초과하는 경로 적분은 존재하지 않습니다.h는 Lagrangian의 파라미터일 뿐이며, 이는 포인트마다 다릅니다.필드의 경로 적분은 다음과 같습니다.
그리고 이것은 모든 점에서의 h 값의 함수이다.이 식을 해석하는 한 가지 방법은 필드 공간에서 푸리에 변환을 취하는 것입니다.R에n 확률 밀도가 있는 경우 확률 밀도의 푸리에 변환은 다음과 같습니다.
푸리에 변환은 진동 지수의 기대치입니다.송신원h(x)가 존재하는 경우의 패스는 다음과 같습니다.
격자에서 각 필드 값에 대한 진동 지수의 곱입니다.
델타 함수의 푸리에 변환은 상수이며, 델타 함수에 대한 공식식을 제공합니다.
경로 적분에서의 필드 델타 함수의 모습을 알 수 있습니다.2개의 스칼라필드 「」와 「」의 경우,
이 값은 푸리에 변환 좌표, h에 걸쳐 적분됩니다.델타 함수가 일반 다차원 적분에서의 좌표를 변경하는 데 사용되는 것처럼 이 식은 경로 적분에서의 필드 좌표를 정식으로 변경하는 데 유용합니다.
파티션 함수는 필드h의 함수가 되고 물리 파티션 함수는 h가 제로 함수일 때의 값입니다.
상관 함수는 소스에 대해 통합된 경로의 파생 함수입니다.
유클리드 공간에서, 작용에 대한 원천 기여는 여전히 i의 계수로 나타날 수 있고, 그래서 그들은 여전히 푸리에 변환을 할 수 있다.
스핀 1/2: "사진" 및 "고스트"
스핀 1/2: Grassmann 내장
필드 경로 적분은 페르미 사례까지 확장할 수 있지만, 적분 개념이 확장되는 경우에만 가능합니다.자유 페르미 필드의 그래스만 적분은 고차원 행렬식 또는 파피안이며, 이는 페르미 필드에 적합한 새로운 유형의 가우스 적분을 정의합니다.
그라스만 통합의 두 가지 기본 공식은 다음과 같습니다.
여기서 M은 임의의 행렬이고 θ, θ는 각 지수 i에 대한 독립적인 그래스만 변수이다.
여기서 A는 반대칭 행렬이고, θ는 Grassmann 변수의 집합이며, 1/2는 이중 이중화를 방지하기 위한 것이다(θθij = -θ이므로ji).
행렬표기법에서 θ와 θ는 그래스만 값 행 벡터이고, θ와 θ는 그래스만 값 열 벡터이고, M은 실값 행렬이다.
여기서 마지막 등식은 그래스만 적분의 변환 불변성의 결과이다.그래스만 변수 θ는 θ의 외부 소스이며, θ에 대한 미분에서는 θ의 풀다운 인자를 구한다.
다시 도식 매트릭스 표기법입니다.위의 공식의 의미는 θ와 θ의 적절한 성분에 대한 도함수가 M의 행렬−1 원소를 제공한다는 것이다.이는 복잡한 보손 필드의 가우스 적분에 대한 보손 경로 적분 공식과 정확히 유사합니다.
따라서 전파자는 Bose와 Fermi의 경우에서 작용의 2차 부분에서 행렬의 역행렬이 됩니다.
실제 그래스만 필드의 경우, 마요라나 페르미온의 경우 경로 적분은 파피아 곱하기 소스 2차 형식이며, 공식은 실제 보손 필드의 경우와 마찬가지로 행렬식의 제곱근을 제공합니다.전파자는 여전히 2차 부분의 역수입니다.
무료 디락 라그랑지안:
일반적인 경로 적분에서의 클라인 고든 라그랑지안이 스칼라 필드의 운동 방정식과 정류 관계를 제공하는 것과 같이, 디락 필드의 운동 방정식과 반소환 관계를 공식적으로 제공합니다.Dirac 필드의 공간 푸리에 변환을 Grassmann 대수의 새로운 기준으로 사용함으로써, Dirac 작용의 2차 부분은 반전이 간단해진다.
전파자는 서로 다른 k 값은 서로 섞이지 않기 때문에 θ(k)와 θ(k)를 링크하는 행렬 M의 역수입니다.
윅의 정리 유추는 and과 in를 쌍으로 일치시킨다.
여기서 S는 and과 to의 순서를 바꿔서 coming가 ψ의 바로 앞에 오도록 쌍으로 된 것을 나란히 배치하는 치환의 부호이다.θ, θ 쌍은 그래스만 대수의 통근 요소이기 때문에 쌍이 어떤 순서로 되든 상관없다.둘 이상의 θ, θ 쌍이 같은 k를 가지면 적분은 0이 되며, 이 경우 합계가 0이 되는 것을 쉽게 확인할 수 있다(항상 짝수가 존재한다).이것은 앞서 보소닉 윅의 정리를 완성한 높은 가우스 모멘트의 그래스만 유사체이다.
스핀 1/2 Dirac 파티클의 규칙은 다음과 같습니다.전파자는 Dirac 연산자의 역수이며, 라인은 복잡한 스칼라 필드와 마찬가지로 화살표가 있으며, 다이어그램은 닫힌 페르미 루프마다 -1의 전체 계수를 획득합니다.페르미 루프가 홀수일 경우 다이어그램은 부호를 변경합니다.역사적으로 -1 법칙은 파인만이 발견하기 매우 어려웠다.그는 그라스만 통합에 대한 적절한 이론이 없었기 때문에 오랜 시행착오 끝에 그것을 발견했다.
이 규칙은 정점에 있는 페르미 선의 수는 항상 짝수라는 관측에서 따랐습니다.라그랑지안의 각 용어는 항상 보손어여야 한다.페르미 루프는 페르미온 선을 따라 시작점으로 돌아간 후 다이어그램에서 해당 선을 제거함으로써 계산된다.이 과정을 반복하면 결국 모든 페르미온 선이 지워집니다. 이것은 그래프에 2색칠을 하는 오일러 알고리즘으로, 각 정점이 짝수 도수를 가질 때마다 작동합니다.오일러 알고리즘의 단계 수는 페르미 필드에서 라그랑지안의 모든 항이 정확히 2차이고, 그래서 각 정점이 정확히 두 개의 페르미온 선을 갖는 일반적인 특수한 경우에 독립적인 페르미온 호몰로지 사이클의 수와 같다.4-페르미 상호작용이 있을 때(약핵 상호작용의 페르미 유효 이론에서와 같이) 페르미 루프보다 더 많은 k-적분이 있다.이 경우, 계수 규칙은 각 정점의 페르미 선을 함께 라그랑지안에서 항의 보손 인자를 형성하는 쌍으로 쌍으로 결합하여 오일러 알고리즘을 적용해야 하며, 정점을 한 선씩 입력할 때 알고리즘은 항상 파트너 선과 함께 떠나야 한다.
규칙을 명확히 하고 증명하기 위해, 페르미온장이 있는 라그랑지안의 항인 꼭지점으로부터 형성된 파인만 도표를 생각해 보세요.완전항은 보소닉이며, 그래스만 대수의 통근 요소이기 때문에 정점이 나타나는 순서는 중요하지 않습니다.페르미 선은 루프로 연결되며 루프를 통과할 때 신호 비용 없이 정점 항을 차례로 정렬할 수 있습니다.단, 시작점으로 돌아가면 마지막 하프라인이 연결되지 않은 첫 번째 하프라인과 결합되어야 합니다.이것은 마지막 ψ을 첫 번째 , 앞으로 이동시키기 위해 하나의 치열이 필요하며, 이것이 기호가 됩니다.
이 규칙은 내부 라인에서 제외 원칙의 유일한 가시적 효과입니다.외부 라인이 있는 경우, 동일한 입자에 대한 두 개의 페르미 삽입이 교환될 때 진폭은 반대칭이 됩니다.페르미 장에 대한 원천은 그라스만에게 가치 있는 것이기 때문에 소스 형식주의에서는 이것이 자동적입니다.
스핀 1: 광자
광자에 대한 순진한 전파자는 무한합니다. 왜냐하면 A장의 라그랑지안은 다음과 같기 때문입니다.
전파자를 정의하는 2차 형식은 반전할 수 없습니다.이유는 필드의 게이지 불변성 때문입니다. A에 구배를 더해도 물리학은 바뀌지 않습니다.
이 문제를 해결하려면 게이지를 고쳐야 합니다.가장 편리한 방법은 A의 분산이 어떤 함수 f가 되도록 요구하는 것이며, 그 값은 포인트 간에 랜덤입니다.f 값은 게이지의 선택만 결정하므로 f의 값에 대해 적분하는 것은 해가 되지 않습니다.이 절차에서는 A의 경로 적분에 다음 요소를 삽입합니다.
첫 번째 요인인 델타 함수는 게이지를 고정합니다.두 번째 요인은 불평등 게이지 고정 장치인 f의 다른 값을 합산합니다.이것은 단순하다.
게이지 고정의 추가 기여는 자유 라그랑지안의 후반부를 취소하여 파인만 라그랑지안을 다음과 같이 만듭니다.
A의 각 컴포넌트에 1개씩 4개의 독립된 무료 스칼라 필드와 같습니다.Feyman 전파자는 다음과 같습니다.
한 가지 차이점은 로렌츠의 경우 하나의 전파기의 부호가 잘못되었다는 것입니다. 즉, 타임라이크 구성요소는 반대 부호 전파기를 가지고 있습니다.이는 이러한 입자 상태가 음의 규범을 가지며 물리적 상태가 아님을 의미합니다.광자의 경우, 이러한 상태가 물리적 상태가 아님을 다이어그램 방법으로 쉽게 보여줄 수 있다. k의 값에 대해 두 개의 물리적 광자 편파 기여만 남기기 위해 세로 방향 광자와 함께 기여가 취소된다.
f에 대한 평균화가 1/2와 다른 계수로 수행되면 두 항이 완전히 취소되지 않습니다.이 결과 공변량 라그랑지안은 계수displaystyle \를 가지며, 이는 아무 영향도 미치지 않습니다.
QED의 공변 전파기는 다음과 같습니다.
스핀 1: 비아벨리아 고스트
비 Abelian 게이지 필드의 Feynman 규칙을 찾으려면 게이지 고정 절차를 신중하게 수정하여 경로 적분 변수 변경을 고려해야 합니다.
게이지 고정 계수에는 델타 함수를 터트리는 추가 결정 요인이 있습니다.
행렬식의 형태를 찾으려면 먼저 각도 θ가 아닌 r에만 의존하는 함수 f의 단순한 2차원 적분을 고려한다.: 위에 적분 삽입:
미분계수는 θ에서 델타함수를 팝핑하면 적분이 제거됨을 보증합니다.통합 순서를 교환하면서
하지만 이제 델타 함수는 y로 표시할 수 있습니다.
적분 over θ는 전체 계수가 2µ인 반면, θ의 변화에 따른 y의 변화율은 x에 불과하므로 이 연습은 방사 함수의 극적분 표준 공식을 재현한다.
nonabelian 게이지 필드의 경로 적분에서는 다음과 같은 조작이 이루어집니다.
앞에 있는 계수는 게이지 그룹의 부피이며, 이 계수는 상수를 기여하며, 이는 폐기될 수 있습니다.나머지 적분은 게이지 고정 동작 위에 있습니다.
공변량 게이지를 얻기 위해 게이지 고정 조건은 아벨리언의 경우와 동일합니다.
극소 게이지 변환에서의 변동은 다음과 같습니다.
여기서 α는 극소 게이지 변환을 수행하는 모든 점에서 Lie 대수의 인접값 요소이다.그러면 Faddeev Popov 결정요인이 액션에 추가됩니다.
Ghost 필드를 도입함으로써 Grassmann 적분으로 다시 작성할 수 있습니다.
행렬식은 f와 독립적이므로 f 위의 경로 적분은 아벨의 경우와 같이 f에 대한 측도를 선택함으로써 파인만 전파기(또는 공변 전파기)를 제공할 수 있습니다.전체 게이지 고정 작용은 파인만 게이지의 Yang Mills 작용과 추가적인 고스트 작용입니다.
다이어그램은 이 액션에서 파생됩니다.spin-1 필드의 전파자는 일반적인 파인만 형식을 가집니다.커플링이 구조 상수인 운동량 계수를 갖는 3도 정점과 커플링이 구조 상수의 산물인 4도 정점이 있습니다.추가 고스트 루프가 있어 A 루프의 타임라이크 스테이트와 세로 스테이트가 상쇄됩니다.
Abelian의 경우 공변 게이지의 행렬식은 A에 의존하지 않으므로 고스트는 연결된 다이어그램에 기여하지 않습니다.
파티클 패스 표현
파인만 다이어그램은 입자 궤도의 다양한 등급에서 S 행렬에 대한 기여도를 나타내는 방법으로 파인만이 시행착오를 통해 처음 발견했다.
슈윙거 표현
유클리드 스칼라 전파자는 시사적인 표현을 가지고 있다.
이 동일성(기본 적분)의 의미는 푸리에가 실제 공간으로 변환함으로써 명확해집니다.
전파기에 대한 임의의 1개의 값에서의 기여는 폭의 가우스이다.0에서 x까지의 총 전파 함수는 정규화된 가우스의 모든 적절한 시간 θ에 걸친 가중치 합이며, 시간 θ의 랜덤 워크 후 x에 도달할 확률입니다.
다음으로 전파자의 경로 적분 표현은 다음과 같습니다.
슈윙거 표현에 대한 경로 적분 개서입니다.
슈윙거 표현은 전파자의 입자 측면을 명확히 하는 것과 루프 다이어그램의 분모를 대칭화하는 데 모두 유용합니다.
분모 결합
슈윙거 표현은 루프 다이어그램에 즉시 실용적으로 적용됩니다.예를 들어, 2개의 x를 2개의 반직선으로 결합하고 나머지 라인을 외부로 함으로써 형성되는 θ4 이론의 다이어그램에서는 루프 내 내부 전파기에서의 적분은 다음과 같습니다.
여기서 한 선은 운동량 k를 전달하고 다른 선은 k + p를 전달한다.모든 것을 Schwinger 표현에 포함시킴으로써 비대칭을 수정할 수 있습니다.
이제 지수는 대부분 t + tθ에 의존합니다.
약간 비대칭적인 것만 빼면요.변수 u = t + tθ 및 v = tθ/u를 정의하면 변수 u는 0에서 θ로, v는 0에서 1로 이동합니다.변수 u는 루프의 총 고유 시간이며 v는 루프의 맨 위에 있는 적절한 시간 대 맨 아래에 있는 적절한 시간의 분수를 매개 변수화합니다.
이러한 변수 변환에 대한 야코비안은 ID에서 쉽게 구할 수 있습니다.
그리고 "웨딩"은
- u d tdu dv 입니다.
이를 통해 u 적분을 명시적으로 평가할 수 있습니다.
v-blocks만 남았습니다.슈윙거에 의해 발명되었지만 보통 파인만이 만든 이 방법은 결합 분모라고 불립니다.추상적으로, 이것은 기본 정체성입니다.
그러나 이 형식은 v를 도입하기 위한 물리적 동기를 제공하지 않습니다. v는 루프의 다리 중 하나에서 적절한 시간의 비율입니다.
분모가 결합되면 k에서 kθ = k + vp로 이동하면 모든 것이 대칭이 됩니다.
이 형태는 p가2 로런츠 공간의 물리적 영역에서 발생하는 루프의 입자 질량의 4배보다 더 음의 순간 적분이 절단을 가지고 있음을 보여준다.이때가 바로 외부 운동량이 물리적 입자를 만들 수 있는 시기입니다.
루프의 정점이 많을 경우 결합할 분모가 많아집니다.
일반적인 규칙은 n + 1 분모에 대한 슈윙거 처방에서 따랐다.
슈윙거 매개변수i u 위의 적분은 이전처럼 총 적정 시간 u0 = u1 + un ... + u에 대한 적분 및 i { {1,2,...n}에 대한 루프i v = ui/u의 첫 번째 세그먼트를 제외한 모든 적절한 시간 비율에 대한 적분으로 분할할 수 있습니다.v는i 양수이고 합계가 1보다 작기 때문에 v 적분은 n차원 심플렉스 위에 있습니다.
좌표 변환을 위한 야코비안은 이전과 같이 계산할 수 있습니다.
이 방정식을 모두 합치면 얻을 수 있다.
이를 통해 적분이 제공됩니다.
여기서 심플렉스는 조건에 의해 정의된 영역입니다.
게다가
u 적분을 수행하면 다음과 같은 분모를 결합하기 위한 일반적인 처방이 제공됩니다.
적분자의 분자는 관여하지 않기 때문에 어떤 스핀이 다리로 운반되든 동일한 처방이 모든 루프에 적용됩니다.매개변수i v의 해석은 각 다리에 소요된 총 적정 시간의 비율이다.
산란
양자장론의 상관 함수는 입자의 산란을 설명한다.상대론적 장 이론에서 "입자"의 정의는 자명하지 않다. 왜냐하면 불확실성이 콤프턴 파장보다 작도록 위치를 결정하려고 하면 에너지의 불확실성은 진공으로부터 더 많은 입자와 반입자를 생성하기에 충분히 크기 때문이다.이것은 단일 입자 상태의 개념이 공간에 국재된 물체의 개념과 어느 정도 양립할 수 없다는 것을 의미합니다.
1930년대에 위그너는 단일 입자 상태에 대한 수학적 정의를 내렸습니다: 그것들은 푸앵카레 그룹의 축소 불가능한 표현을 형성하는 상태의 집합입니다.단일 입자 상태는 유한 질량, 잘 정의된 운동량 및 스핀을 가진 물체를 나타냅니다.이 정의는 양성자와 중성자, 전자와 광자에 대해서는 괜찮지만, 영구적으로 제한되는 쿼크는 제외됩니다. 따라서 현대의 관점은 입자가 입자 궤적을 합한 것으로 해석되는 파인만 다이어그램의 관점에서 설명될 수 있는 어떤 것이든 더 적합합니다.
필드 연산자는 진공으로부터 1개의 입자 상태를 생성하기 위해 동작할 수 있으며, 이는 필드 연산자 δ(x)가 위그너 입자 상태의 중첩을 생성함을 의미한다.자유장 이론에서 장은 하나의 입자 상태만 생성합니다.그러나 상호작용이 있을 경우 필드 연산자는 3 입자, 5 입자(+/- 대칭이 없는 경우 2, 4, 6 입자) 상태도 생성할 수 있습니다.단일 입자 상태에 대한 산란 진폭을 계산하려면 신중한 제한만 필요하며, 필드를 무한대로 보내고 공간에 통합하여 고차 보정을 제거합니다.
산란 함수와 상관 함수 간의 관계는 LSZ 이론입니다.산란 이벤트에서 n개의 입자가 m개의 입자로 가는 산란 진폭은 외부 레그용 전파기를 제외하고 n+m 필드 삽입에 대한 상관 함수에 들어가는 파인만 다이어그램의 합으로 주어진다.
예를 들어, 이전 섹션의 δ상호작용의4 경우 (로렌츠) 상관함수에 대한 순서 δ상관함수의 기여도는 다음과 같습니다.
외부 전파기를 제거하면, 즉 i/k의2 계수를 제거하면 불변 산란 진폭 M이 다음과 같이 됩니다.
이는 유입 및 발신 모멘텀과는 무관한 일정한 모멘텀입니다.산란 진폭의 해석은 가능한 모든 최종 상태에 대한 M의 합이 산란 이벤트의 확률이라는 것이다.단, M이 상대론적 불변량임을 보증하기 위해 단입자 상태의 정규화는 신중하게 선택되어야 한다.
비상대론적 단일 입자 상태는 운동량 k로 표시되며 k의 모든 값에서 동일한 규격을 갖도록 선택됩니다.이는 단일 입자 상태의 비상대론적 단위 연산자가 다음과 같기 때문입니다.
상대성 이론에서 질량 m 입자에 대한 k-상태 위의 적분은 에너지-모멘텀 관계에 의해 정의된 E.k 공간의 쌍곡선 위에 통합된다.
적분의 무게가 각 k개의 점에 균등하다면 측정값은 로렌츠 불변수가 아닙니다.불변 측도는 k와 E의 모든 값에 통합되어 로렌츠 불변 델타 함수의 쌍곡선으로 제한됩니다.
그래서 정규화된 k-상태는 상대적으로 정규화된 k-상태와는 다음의 요인에 의해 다르다.
불변 진폭 M은 상대적으로 정규화된 착신 상태가 상대적으로 정규화된 발신 상태가 될 확률 진폭입니다.
k의 비상대론적 값의 경우 상대론적 정규화는 비상대론적 정규화와 동일하다(최대 상수 인자 δm).이 한계에서는 δ4 불변 산란 진폭이 여전히 일정합니다.필드 θ에 의해 생성된 입자는 동일한 진폭으로 모든 방향으로 산란한다.
(Born 근사에서) 동일한 진폭으로 모든 방향으로 산란되는 비상대론적 전위는 푸리에 변환이 일정한 전위, 즉 델타 함수 전위입니다.이론의 가장 낮은 차수의 산란은 이 이론의 비상대론적 해석을 드러낸다. 즉, 델타 함수 반발이 있는 입자의 집합을 설명한다.그러한 두 입자는 동시에 같은 지점을 점유하는 것을 싫어한다.
비교란 효과
파인만 다이어그램을 섭동 급수로 생각하면 터널링과 같은 비교란 효과는 나타나지 않습니다. 왜냐하면 어떤 다항식보다 빨리 0으로 가는 효과는 테일러 급수에 영향을 주지 않기 때문입니다.어떤 유한 차수의 입자가 유한한 횟수만 교환되기 때문에 결합력은 존재하지 않으며 결합 상태를 만들기 위해 결합력은 영원히 지속되어야 한다.
그러나 이 관점은 오해의 소지가 있다.왜냐하면 도표는 산란을 묘사할 뿐만 아니라 단거리 자기장 이론의 상관관계를 나타내고 있기 때문입니다.이들은 입자 산란과 같은 점근 프로세스를 부호화할 뿐만 아니라 필드의 곱셈 규칙, 연산자 곱셈 확장도 기술합니다.비교란 터널링 프로세스에는 결합 정수가 작아지면 평균적으로 커지는 필드 구성이 포함되지만 각 구성은 로컬 상호작용이 파인만 다이어그램으로 설명되는 입자의 일관된 중첩입니다.하지만 각 입자들의 사이의 상호 작용의 단순한 입자들의 큰 숫자들을 포함할 때 연결 장치 작은 것은, 이가 집단적인 과정이다.[표창 필요한](어떤 상호 작용하는 양자장론의 섭동 시리즈, 도표(의 제한치에 필요한 무한한 시리즈의 한계 복잡하게 수렴 제로의 반경이.소실되는 커플링)을 사용하여 이러한 필드 구성을 설명합니다.)
즉, 비교란 효과가 무한 클래스의 다이어그램 재설명에 점근적으로 나타나며, 이러한 다이어그램은 국소적으로 단순할 수 있다.그래프는 국소 운동 방정식을 결정하는 반면, 허용되는 대규모 구성은 비교란 물리학을 설명합니다.그러나 Feynman 전파자는 시간적으로 로컬이 아니기 때문에 필드 프로세스를 일관된 입자 언어로 번역하는 것은 완전히 직관적인 것은 아니며 특정 특수한 경우에만 명시적으로 해결되었습니다.비상대론적 한계 상태의 경우, 베테-살페터 방정식은 상대론적 원자를 기술하기 위해 포함하는 다이어그램의 클래스를 기술한다.양자 색역학의 경우, 시프만-베인슈타인-자하로프 총합 규칙은 입자 언어로 비교란적으로 들뜬 장파장 모드를 기술하지만, 현상학적 방식으로만 기술합니다.
섭동 이론의 높은 차수의 파인만 다이어그램의 수는 매우 큽니다. 주어진 수의 노드를 가진 그래프만큼 많은 다이어그램이 있기 때문입니다.비교란 효과는 도표와 재질의 수가 높은 순서로 분산되는 방식에 흔적을 남깁니다.비교란 효과가 그림에서 숨겨진 형태로 나타나기 때문에 많은 경우 파인만 기술만이 이용 가능한 끈 이론에서 비교란 효과를 분석할 수 있었다.
대중문화에서
- 쿼크-반쿼크 쌍을 생성하는 가상 입자의 위 다이어그램의 사용은 텔레비전 시트콤 빅뱅 이론의 에피소드 "박쥐 항아리 추측"에서 다루어졌습니다.
- 2012년 1월 11일자 PhD Comics에서는 양자학문의 상호작용, 즉 [11]지도교수와 상호작용할 때 박사과정 학생들이 따르는 경로를 시각화하고 설명하는 Feyman 다이어그램을 보여줍니다.
- 진공도(Vacuum Diagraph)는 스티븐 백스터의 공상과학 소설로 파인만 다이어그램의 특정 유형인 명목 진공도를 특징으로 한다.
- 파인만과 그의 아내 그웨네스 하워스는 1975년에 닷지 트레이즈맨 맥시반을 사서 파인만 [12]도표로 그림을 그리게 했다.
「 」를 참조해 주세요.
메모들
- ^ "파인만의 시각적 통찰력이 어떻게 사용될 수 있는지를 보여주는 것은 다이슨의 공헌이었다. 그는 파인만 도표가 (그들의 섭동적 확장에 명시된) 필드 이론의 논리적인 내용을 나타내는 것으로도 보일 수 있다는 것을 깨달았다."슈베버, op.cit (1994)
레퍼런스
- ^ Kaiser, David (2005). "Physics and Feynman's Diagrams" (PDF). American Scientist. 93 (2): 156. doi:10.1511/2005.52.957.
- ^ "Why Feynman Diagrams Are So Important". Quanta Magazine. 5 July 2016. Retrieved 2020-06-16.
- ^ Feynman, Richard (1949). "The Theory of Positrons". Physical Review. 76 (6): 749–759. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
In this solution, the 'negative energy states' appear in a form which may be pictured (as by Stückelberg) in space-time as waves traveling away from the external potential backwards in time. Experimentally, such a wave corresponds to a positron approaching the potential and annihilating the electron.
- ^ Penco, R.; Mauro, D. (2006). "Perturbation theory via Feynman diagrams in classical mechanics". European Journal of Physics. 27 (5): 1241–1250. arXiv:hep-th/0605061. Bibcode:2006EJPh...27.1241P. doi:10.1088/0143-0807/27/5/023. S2CID 2895311.
- ^ George Johnson (July 2000). "The Jaguar and the Fox". The Atlantic. Retrieved February 26, 2013.
- ^ Gribbin, John; Gribbin, Mary (1997). "5". Richard Feynman: A Life in Science. Penguin-Putnam.
- ^ Mlodinow, Leonard (2011). Feynman's Rainbow. Vintage. p. 29.
- ^ Gerardus 't Hooft, Martinus Veltman, Diagramar, CERN Yellow Report 1973, G. 't Hooft, "게이지의 마법 아래"에 전재(World Scientific, Singapore, 1994), 온라인 소개
- ^ 마르티누스 벨트만, 다이어그램매티카: 파인만 도표, 케임브리지 물리학 강의 노트, ISBN 0-521-45692-4
- ^ Bjorken, J. D.; Drell, S. D. (1965). Relativistic Quantum Fields. New York: McGraw-Hill. p. viii. ISBN 978-0-07-005494-3.
- ^ Jorge Cham, 학술적 상호작용 – Feyman 다이어그램, 2012년 1월 11일
- ^ Jepsen, Kathryn (2014-08-05). "Saving the Feynman van". Symmetry Magazine. Retrieved 2022-06-23.
원천
- 't Hooft, Gerardus; Veltman, Martinus (1973). "Diagrammar". CERN Yellow Report. doi:10.5170/CERN-1973-009.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - Kaiser, David (2005). Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics. Chicago, IL: University of Chicago Press. ISBN 0-226-42266-6.
- Veltman, Martinus (1994-06-16). Diagrammatica: The Path to Feynman Diagrams. Cambridge Lecture Notes in Physics. ISBN 0-521-45692-4. (위에서 인용한 't Hooft & Veltman, 1973'의 확장판 업데이트 버전)
- Srednicki, Mark (2006). Quantum Field Theory. Script.
- Schweber, S. S. (1994). QED and the men who made it: Dyson, Feynman, Schwinger, and Tomonaga. Princeton University Press. ISBN 978-0691033273.
외부 링크
- AMS 기사: "수학 신기능:유한 차원 파인만 다이어그램"
- Flip Tanedo가 설명한 Feyman 다이어그램을 Quantumdiaries.com에서 그립니다.
- PostScript 출력을 생성하는 FeynDiagram C++ 라이브러리를 사용하여 Feyman 다이어그램을 그립니다.
- 온라인 다이어그램 도구 출판 준비 다이어그램을 만들기 위한 그래픽 응용 프로그램입니다.
- JaxoDraw 파인만 다이어그램을 그리기 위한 Java 프로그램입니다.
- Bowley, Roger; Copeland, Ed (2010). "Feynman Diagrams". Sixty Symbols. Brady Haran for the University of Nottingham.


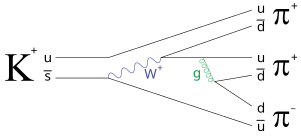








 i 점 x에 부착된 꿈틀거리는 선으로 나타납니다.
i 점 x에 부착된 꿈틀거리는 선으로 나타납니다.





















































![iW[J]\equiv \ln Z[J].](https://wikimedia.org/api/rest_v1/media/math/render/svg/a03aef8a72b98aa83afeccb54512c30e74dd0762)
![Z[J]\propto \sum _{k}{D_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c7b6e822c008b3a97c2e25ae9a16d806decc9e7)


![{\displaystyle Z[J]\propto \prod _{i}{\sum _{n_{i}=0}^{\infty }{\frac {C_{i}^{n_{i}}}{n_{i}!}}}=\exp {\sum _{i}{C_{i}}}\propto \exp {W[J]}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50886f901a854ec595c3b9727199e105ad57b73f)




![{\displaystyle \log {\big (}Z[h]{\big )}=\sum _{n,C}h(k_{1})h(k_{2})\cdots h(k_{n})C(k_{1},\cdots ,k_{n})\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7bb5547d19ab5fdb64ff700ecc8e3835311e446c)
![{\displaystyle Z[h]=\int e^{iS+i\int h\phi }\,D\phi \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7ea2bd0c5073e68ceff5ddba15e555ce70f92a6)

![{\displaystyle Z[h]=\int e^{iS}e^{i\int _{x}h(x)\phi (x)}\,D\phi =\left\langle e^{ih\phi }\right\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b66d7bcdfcff36ef81756bc3cda53721bd81d685)



![{\displaystyle \left\langle \phi (x)\right\rangle ={\frac {1}{Z}}{\frac {\partial }{\partial h(x)}}Z[h]={\frac {\partial }{\partial h(x)}}\log {\big (}Z[h]{\big )}\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/370ee6c83d4c8ed003752105106c84371401dfa1)


























































