호몰로지(수학)

수학에서 호몰로지(homology^[1])는 아벨리아 그룹이나 모듈과 같은 대수적 물체의 순서를 위상학적 공간과 같은 다른 수학적 물체와 연관시키는 일반적인 방법이다. 호몰로지 그룹은 원래 대수적 토폴로지에서 정의되었다. 이와 유사한 구조는 추상 대수학, 집단, 리 알헤브라스, 갈루아 이론, 대수 기하학 등 매우 다양한 다른 맥락에서 이용할 수 있다.

호몰로지 집단을 규정하는 최초의 동기는 두 개의 모양이 구멍을 조사함으로써 구별될 수 있다는 관찰이었다. 예를 들어 원은 원반이 단단한 상태에서 구멍이 뚫려 있기 때문에 원형이 원반이 아니며, 원은 1차원 구멍을 감싸는 반면, 구는 2차원 구멍을 감싸기 때문에 일반 구체는 원형이 아니다. 그러나 구멍이 '없음'으로 되어 있기 때문에, 구멍을 어떻게 정의해야 하는지, 혹은 다른 종류의 구멍을 어떻게 구분해야 하는지가 즉각적으로 명확하지 않다. 호몰로지(homology)는 원래 다지관의 구멍을 정의하고 분류하는 엄격한 수학적 방법이었다. 느슨하게 말하면 주기는 닫힌 하위 관리형이고 경계는 하위 관리형의 경계이기도 한 주기이며, 호몰로지 클래스(구멍을 나타냄)는 주기 모듈로 경계의 동등성 등급이다. 따라서 호몰로지 클래스는 하위 관리형의 경계가 아닌 순환으로 표현된다. 즉, 순환은 구멍, 즉 그 경계가 "거기 없다"는 가상의 다지관을 나타낸다.

많은 다양한 호몰로지 이론들이 있다. 위상학적 공간이나 그룹과 같은 특정한 유형의 수학 물체는 하나 이상의 연관된 호몰로지 이론을 가질 수 있다. 기초적인 물체가 위상학적 공간처럼 기하학적 해석을 갖는 경우, n번째 호몰로지 그룹은 차원 n에서 행동을 나타낸다. 대부분의 호몰로지 그룹 또는 모듈은 정확한 펑터의 고장을 측정하여 적절한 아벨리아 범주에 대한 파생 펑터로 공식화될 수 있다. 이러한 추상적인 관점에서 호몰로지 집단은 파생된 범주의 객체에 의해 결정된다.

배경

오리진스

호몰로지 이론은 오일러 다면체 공식, 즉 오일러 특성에서 출발한다고 말할 수 있다.^[2] 이는 1857년 리만(Riemann)이 속과 n-폴드 연결성 수적 불변제를 정의하고, 1871년 베티가 근거의 선택으로부터 "동성 수"의 독립성을 입증한 데 이은 것이다.^[3]

호몰로지 자체는 다지관의 주기에 따라 분석 및 분류하는 방법으로 개발되었다. 즉, 주어진 n차원 다지관에 그릴 수 있지만 서로 지속적으로 변형되지는 않는 폐쇄 루프(또는 보다 일반적으로 서브매니폴드)이다.^[4] 이러한 사이클은 다시 붙일 수 있는 절단부 또는 고정되고 풀릴 수 있는 지퍼로도 생각되기도 한다. 사이클은 치수에 따라 분류된다. 예를 들어 표면에 그려진 선은 1주기, 닫힌 루프 또는 S ${\$1-manifold)를 나타내며, 3차원 다지관을 통해 절단된 표면은 2주기라고 한다.

표면

보통의 구 S ${\$에서는 도표의 사이클 b를 극으로 축소할 수 있으며, 적도 대원 a도 같은 방법으로 축소할 수 있다$.$ 요르단 곡선 정리는 c와 같은 임의의 사이클이 비슷하게 한 점으로 축소될 수 있음을 보여준다. 따라서 구의 모든 사이클은 지속적으로 서로 변형될 수 있으며 동일한 호몰로지 클래스에 속한다. 그들은 0과 동음이의어라고 한다. 균일 균일성을 따라 매니폴드를 0으로 절단하면 매니폴드가 두 개 이상의 구성 요소로 분리된다. 예를 들어 구를 자르면 두 개의 반구가 생긴다.

이것은 일반적으로 다른 표면의 사이클에 해당되지 않는다. Torus $T{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$개의 사이클은 서로 연속적으로 변형될 수 없는 사이클을 가지고$$ 있다. 예를 들어 다이어그램에서 어떤 사이클도 서로 변형될 수 없다. 특히 a와 b 사이클은 한 점으로 축소할 수 없는 반면 c 사이클은 한 점으로 축소할 수 없으므로 0에 동음이의어가 된다.

토러스 표면을 a와 b 둘 다 따라 자르면, 그것을 펼쳐서 직사각형 또는 더 편리하게 사각형으로 납작하게 만들 수 있다. 한 쌍의 반대쪽은 a를 따라 절단을 나타내고, 다른 쌍의 반대쪽은 b를 따라 절단을 나타낸다.

그러면 사각형의 가장자리는 다른 방식으로 다시 접착될 수 있다. 다이어그램의 화살표와 같이 사각형을 비틀어 가장자리가 반대 방향으로 만날 수 있다. 대칭까지, 옆면을 접착하는 네 가지 뚜렷한 방법이 있는데, 각각 다른 표면을 만든다.

${\displaystyle K^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$은 클라인 병으로, 반전이 있는 토러스(반전은 사각형 도표에서 아래쪽 화살표의 반전이라고 볼 수 있다. 재융기된 표면이 스스로 교차해야 하는 정리(유클리드 3공간에 담길 때)이다. 토러스처럼 a와 b 사이클은 c 사이클이 줄어들 수 없는 반면 c 사이클은 줄어들 수 없다. 그러나 토러스와는 달리, b를 따르는 것은 오른쪽 회전을 앞쪽으로 향하게 되고, b는 한 조인트에 주어지는 트위스트를 넘어 좌우로 반전하게 된다. b의 한쪽 면에 등거리 절단이 이루어지면 다른 면으로 돌아와 두 번째로 표면을 돌고 다시 출발점으로 돌아가면서 꼬인 뫼비우스 띠를 잘라낸다. 국부 좌우를 이런 식으로 임의로 재지향할 수 있기 때문에 표면 전체는 방향성이 떨어진다고 한다.

투사 평면 $P{\displaystyle {}^{}}$ ${\$ P$^{2}}$번 양쪽 조인트가 꼬였다$$. 일반적으로 보이 표면으로 표현되는 미선형 형태는 시각적으로 복잡하기 때문에 도표에는 반구형 임베딩이 나타나 있는데, 이 경우 A, A와 같이 림의 테두리를 둘러싼 반향형 포인트가 동일한 포인트로 식별된다. 다시 말하지만, a와 b는 c가 있는 동안 수축을 할 수 없다. 그러나 이번에는 a와 b 둘 다 좌우로 역행한다.

토러스 위의 a와 b는 절개하여 납작하게 만들었을 때처럼 사이클을 결합하거나 함께 추가할 수 있다. 클라인 병 도표에서 a는 한 방향으로 돌고 -a는 반대 방향으로 돈다. a를 절단이라고 생각하면 -a는 접착 작업으로 생각할 수 있다. 자른 다음 다시 붙이면 표면이 바뀌지 않으므로 +(-a) = 0이다.

그러나 이제 두 개의 a-cycle을 고려해보자. 클라인 병은 방향성이 없기 때문에 그 중 한 병을 (b 사이클을 따라) 병 주위를 돌 수 있으며 -a로 돌아온다. 이것은 클라인 병이 실린더로 만들어져 있고, 그 실린더의 끝부분은 반대 방향과 함께 접착되어 있기 때문이다. 따라서 2a = a + a = a = a + (-a) = 0. 이러한 현상을 비틀림이라고 한다. 마찬가지로 투영 평면에서 수축되지 않는 주기 b 라운드를 두 번 반복하면 한 점으로 축소될 수 있는 사소한 주기(b + b = 0). 제로 사이클을 달성하려면 b를 두 번 정도 따라야 하기 때문에 표면의 비틀림 계수는 2라고 한다. 그러나 클라인 병에서 b 사이클을 두 번 반복하면 이 사이클은 비틀림 없는 호몰로지 클래스에 있기 때문에 b + b = 2b가 된다. 이는 클라인 병의 기본 폴리곤에서는 한쪽 면만 꼬임으로 접착되어 있는 반면 투영면에서는 양쪽이 꼬임되어 있다는 사실에 해당한다.

사각형은 계약 가능한 위상학적 공간인데, 이것은 그것이 사소한 호몰로지를 가지고 있음을 암시한다. 결과적으로, 추가 절단은 그것의 연결을 끊는다. 평면에서 표면에 붙일 수 있는 형태는 사각형만이 아니다. 예를 들어, 팔각형의 반대편에 접착하면 두 개의 구멍이 있는 표면이 생성된다. 실제로 모든 닫힌 표면은 일부 폴리곤의 옆면을 접착하여 제작할 수 있으며, 모든 짝수 폴리곤(2n-gon)을 접착하여 다른 다지관을 만들 수 있다. 반대로 0이 아닌 클래스가 n개인 닫힌 표면을 2n곤으로 절단할 수 있다. 변형도 가능하다. 예를 들어 육각형을 접착하여 토러스를 형성할 수도 있다.^[5]

최초의 인정받을 수 있는 호몰로지 이론은 앙리 푸앵카레에 의해 그의 세미논문 "Analysis situs", J. Ecole polytech. (2) 1.1–121 (1895)에 발표되었다. 그 신문은 호몰로지 수업과 관계를 소개했다. 방향성 사이클의 가능한 구성은 다지관의 베티 번호로 분류된다(베티 번호는 오일러 특성의 개선이다). 방향성이 없는 사이클을 분류하려면 비틀림 계수에 대한 추가 정보가 필요하다.^[4]

1마니폴드와 2마니폴드의 완전한 분류가 표에 제시되어 있다.

폐쇄형 1-매니폴드 및 2-매니폴드의^[6] 위상학적 특성

다지관		오일러 노. χ	방향성	베티 수			비틀림 계수 (1차원)
기호[5]	이름			b0	b1	b2
${\displaystyle S^{1}$	원(1-manifold)	0	오리엔테이블	1	1	해당 없음	해당 없음
${\displaystyle S^{2}}$	구	2	오리엔테이블	1	0	1	없음
${\displaystyle T^{2}}$	토러스	0	오리엔테이블	1	2	1	없음
${\displaystyle P^{2}}$	투영면	1	방향성이 없음	1	0	0	2
${\displaystyle K^{2}}$	클라인 병	0	방향성이 없음	1	1	0	2
	2홀 토러스	−2	오리엔테이블	1	4	1	없음
	g-홀드 토러스(g는 속이다)	2 − 2g	오리엔테이블	1	2g	1	없음
	c 교차 캡이 있는 구	2 − c	방향성이 없음	1	c − 1	0	2
	2-g홀과 c 크로스캡이 있는 manifold (c > 0)	2 − (2g + c)	방향성이 없음	1	(2g + c) − 1	0	2

메모들

1. 방향성이 없는 표면의 경우 구멍은 두 개의 교차 캡과 같다.
2. 모든 2-매니폴드는 g tori와 c 투영 평면의 연결된 합이다. 구체 $S{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$, g = c = 0.

일반화

경계 또는 개방 다지관이 있는 다지관은 닫힌 다지관과 지형적으로 구별되며 적합한 닫힌 다지관을 절단하여 만들 수 있다. 예를 들어 디스크나 1볼 $B{\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$ ${\$ 스타일 $B$$^{1}$는 원 S ${\displaystyle {1\mathrm{}}^{}}$ ${\$ 스타일 $S$$^{1}$에 의해 경계된다$.$ 2마니폴드에서 사소한 주기를 자르고 조각을 떼어낸 상태로 유지하거나 구를 뚫고 구멍을 넓게 벌리거나 돌출면을 절단하여 만들 수 있다. 그것은 또한 비행기에서 원을 채우는 것으로도 볼 수 있다.

두 사이클이 연속적으로 서로 변형될 수 있을 때, 한 사이클을 따라 자르는 것은 다른 사이클을 따라 자르는 것과 같은 형상을 만들어내며, 어느 정도 구부러지고 스트레칭된다. 이 경우 두 사이클은 동음이의어이거나 같은 동음이의어 등급에 놓여 있다고 한다. 또한, 한 사이클이 연속적으로 다른 사이클의 조합으로 변형될 수 있는 경우, 초기 사이클을 따라 절단하는 것은 다른 사이클의 조합을 따라 절단하는 것과 동일하다. 예를 들어 그림 8을 따라 자르는 것은 두 개의 로브를 따라 자르는 것과 같다. 이 경우 그림 8은 그 로브의 합과 동음이의어라고 한다.

경계가 유사한 두 개의 개방 다지관(일부 구부림 및 스트레칭까지)을 접착하여 연결된 새 다지관을 형성할 수 있다.

다지관의 이 기하학적 분석은 엄격하지 않다. 더욱 엄격해진 엄격함을 찾기 위해 푸앵카레는 삼각형 다지관의 단순한 호몰로지 개발과 현재 체인 콤플렉스라고 불리는 것을 창조하기 위해 계속 나아갔다.^[7][8] 이러한 연쇄 복합체들은 (매우 일반화된 이후) 대부분의 현대적인 동종학 치료의 기초를 형성한다.

이러한 치료에서는 주기가 연속적일 필요가 없다. 0 사이클은 점 집합이며, 이 사이클을 따라 절단하는 것은 다지관을 뚫는 것과 일치한다. 1 사이클은 닫힌 루프 집합에 해당한다(1-manifold ${\displaystyle {S\mathrm{}}^{}}$ $1{\displaystyle {}^{}}$ ${\$ S$^{1}).$ 표면에서 1사이클을 따라 자르면 분리된 조각이나 단순한 모양이 나온다. 2 사이클은 구체나 토러스 등과 같은 내장 표면의 집합에 해당한다.

에미 노에더와 독립적으로 레오폴드 비에토리스와 발터 메이어는 1925-28년에 대수학 호몰로지 그룹 이론을 더욱 발전시켰다.^[9][10][11] 새로운 결합 위상은 공식적으로 위상학 계급을 아벨 집단으로 취급했다. 호몰로지 집단은 정교하게 생성된 아벨리우스 집단이며, 호몰로지 계급은 이들 집단의 요소들이다. 다지관의 베티 번호는 호몰로지 그룹의 자유 부분의 등급이며, 방향성이 없는 주기는 비틀림 부분으로 설명된다.

이후 동질학 집단의 확산은 "복합적 위상"에서 "알지브라질 위상"^[12]으로 용어와 관점의 변화를 가져왔다. 대수적 호몰로학은 다지관을 분류하는 일차적인 방법으로 남아 있다.^[13]

비공식적 예

위상학적 공간 X의 호몰로지(homology)는 그 호몰로지 집단으로 대표되는 X의 위상학적 불변성의 집합체다.

${\displaystyle H_{0}(X),H_{1}(X),H_{2}(X),\ldots }$

$여기$서 k ${\displaystyle {\mathrm{h}}^{}}$ ${\$ k$^{\rm {th}}$ 호몰로지$$ 그룹 ${\displaystyle H_{}}$ $k{\displaystyle {}_{}}$ ${\displaystyle {}_{}X}$) ${\displaystyle H_{k}(X)}$는 X에 있는 k-차원 구멍의 수를 비공식적으로$$ 설명한다. 0차원 구멍은 단순히 두 구성 요소 사이의 간극이다. 따라서 H ${\displaystyle 0{}_{}}$( X${\displaystyle }$) ${\displaystyle H_{0}(X)}$은(는) X의 경로 연결 구성요소를 설명한다$$.^[14]

1차원 구 S ${\$ S$^{1}$는 원이다. 단일 연결 부품과 1차원 구멍이 있지만 고차원 구멍은 없다. 해당 호몰로지 그룹은 다음과 같이 주어진다.

${\displaystyle H_{k}\left(S^{1}\오른쪽)={\begin{case}\mathb {Z} &k=0,1\\\\{0\}\text{otherwise}\end{case}}}}}}}}$

여기서 $Z{\displaystyle \mathbb{}}$ ${\$은$($는) 정수 ${\displaystyle \mathrm{그룹}}$이고${\displaystyle }${ 0${\displaystyle \}}$ ${\displaystyle \{0\}}$은(는) 사소한 그룹이다. ${\displaystyle 그룹\mathbb{}}$ $H{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$)${\displaystyle }$= Z ${\$ {$Z}}$은 원 안에 포함된 1차원 구멍을 나타내는 단일 생성기와 함께 정밀하게 생성된 아벨리아 그룹을 나타낸다$$.^[15]

2차원 구체 ${\$개에는 단일 연결성분이 있고$$, 1차원 구멍이 없으며, 2차원 구멍이 없으며, 고차원 구멍이 없다. 해당^[15][16] 호몰로지 그룹은

${\displaystyle H_{k}\left(S^{2}\오른쪽)={\begin{case}\mathb {Z} &k=0,2\\\{0\}\\text}{otherwise}\end{case}}}}}}}}$

일반적으로 n차원 ${\displaystyle {구}^{}}$ S $n{\displaystyle {}^{}}$, ${\displaystyle$ S$^{n}}$의 경우$$ 호몰로지 그룹은

${\displaystyle H_{k}\left(S^{n}\오른쪽)={\begin{case}\mathb {Z} &k=0,n\\\{0\}&{\text}\otherwise}\end{case}}}}}}}}}}$

2차원 공 $B{\displaystyle {}^{}}$ ${\$은 솔리드 디스크다$$. 단일 경로연계 구성요소를 가지고 있지만, 원과 대조적으로 1차원 또는 고차원적인 구멍이 없다. 해당 호몰로지 그룹은 ${\displaystyle H\mathbb{}}$ ${\displaystyle {0\mathrm{}}_{}{B\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$)${\displaystyle }$= Z ${\$을(를) 제외하고 모두 사소한 것이다. 일반적으로 n차원 $공{\displaystyle {}^{}}$ ${\displaystyle B^{}}$n$,$ {\$displaystyle$B^{$n}$에 대해.

${\displaystyle H_{k}\left(B^{n}\오른쪽)={\begin{case}\mathb {Z} &k=0\\\\{0\}\text{otherwise}\end}}}}}}}}}$

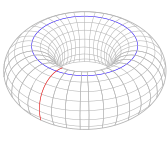
Torus는 두 개의 원 $T{\displaystyle }$= ${\displaystyle {S\mathrm{}}^{}}$ 1 ${\displaystyle {}^{}}$ S ${\displaystyle {1\mathrm{}}^{}}${\$displaystyle T=S^{1}\time S^{$1}의$$곱으로 정의된다$.$ 토러스 내부에는 하나의 경로로 연결된 구성 요소, 두 개의 독립적인 1차원 구멍(빨간색과 파란색으로 원을 그리며 표시)과 1개의 2차원 구멍이 있다. 해당^[17] 호몰로지 그룹은

${\displaystyle H_{k}(T)={\begin{case}\mathb {Z} &k=0,2\\\\mathb {Z} \time \mathb {Z} \notherwise}\case{case}}\end}}$

두 개의 독립적인 1차원 구멍은 제품 그룹 $Z{\displaystyle \mathbb{}}$ ${\displaystyle \times }$ ${\displaystyle Z\mathbb{}.}$ ${\displaystyle \mathb {Z} \time \mathb {Z}$로 표현되는 정밀하게 생성된 아벨리안 그룹에서 독립 생성기를 형성한다$.$

투영 평면 P의 경우 간단한 계산이 표시된다(여기서 ${\displaystyle {\mathrm{}}_{}}$ 2 ${\$은 순서 2의 순환 그룹임).^[18]

${\displaystyle H_{k}(P)={\begin{case}\mathb {Z} &k=0\\\\\mathb {Z} _{2}&k=1\\\{0\}{otherwise}\ext}\case}}}}}}}}\case}}}}}}}}}}?$

${\displaystyle {}_{}H\mathbb{}}$ ${\displaystyle {0\mathrm{}}_{}}$( ${\displaystyle P}$)${\displaystyle }$= Z ${\$은(는) 앞의 예와 같이 하나의 연결된 구성요소가 있다는 사실에 해당한다$$. ${\displaystyle H_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle P}$)${\displaystyle }$= Z ${\displaystyle {\mathrm{}}_{}}$ ${\$}}은$$ 새로운 현상: 직관적으로 단일 비계약 "루프"가 있다는 사실과 일치하지만, 두 번 루프를 하면 0으로 수축할 수 있게 된다. 이 현상을 비틀림이라고 한다.

호몰로지 그룹 구성

공사는 위상학적 공간 X와 같은 물체로 시작되는데, 그 위에서 먼저 X에 대한 체인 콤플렉스 C(X) 인코딩 정보를 정의한다. 체인 콤플렉스는 아벨 그룹 또는 모듈 C ${\displaystyle {0\mathrm{}}_{}}$ C ${\displaystyle {}_{}}$,${\displaystyle {}_{}{C\mathrm{}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle }$… ${\displaystyle C_{0}, C_{1}, C_{2},\ldots$ $\}$의 시퀀스로서 동형체${\displaystyle {\mathrm{}}_{ismsn}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{n}_{}}$ →${\displaystyle {\mathrm{C}}_{}}$ -${\displaystyle {}_{}}$1,$${\$displaysty \partial _{n}:$경계 연산자라고 하는$$ C_{^[17]$n}\to C_{n-1}.$ 그것은

${\displaystyle \dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\partial _{0}}{\longrightarrow \,}}0}$

여기서 0은 사소한 그룹과 i < 0에 대한$$ $C{\displaystyle {}_{}}$ i${\displaystyle {}_{}{i}_{}}$ ${\displaystyle 0}$ ${\displaystyle C_{i}\equiv$ 0$}$을 의미한다. 또한 두 개의 연속된 경계 연산자의 구성은 사소한 것이어야 한다. 즉, 모든 n에 대해,

${\displaystyle \properties _{n}\put \properties _{n+1}=0_{n+1,n-1}$

i.e., the constant map sending every element of ${\displaystyle C_{n+1}}$ to the group identity in ${\displaystyle C_{n-1}.}$The statement that the boundary of a boundary is trivial is equivalent to the statement that ${\displaystyle \mathrm {im} (\partial _{n+1})\$$subseteq$ $\$$ker$(\$display$\cker(\$reason$ $_{$$n})$ ,$$여기서 i ${\displaystyle \mathrm{m}(}$ ${\displaystyle {\mathrm{}}_n}$+ ${\displaystyle 1_{}}$) ${\displaystyle \matrm {im}(\property$ _${n1})$은 경계$$ 연산자 및 $(({n})$ 커널의 이미지를 나타낸다$$. Elements of ${\displaystyle B_{n}(X)=\mathrm {im} (\partial _{n+1})}$ are called boundaries and elements of ${\displaystyle Z_{n}(X)=\ker(\partial _{n})}$ are called cycles.

각각의 체인 그룹 C는_n 아벨리안이기 때문에 모든 하위 그룹은 정상이다. Then because ${\displaystyle \ker(\partial _{n})}$ is a subgroup of C_n, ${\displaystyle \ker(\partial _{n})}$ is abelian, and since ${\displaystyle \mathrm {im} (\partial _{n+1})\leq \ker(\partial _{n})}$ therefore ${\displayst$$yle \mathrm {im}(\reason _{n+1})$은 ${\displaystyle \ker }$ ${\displaystyle }$ ( ${\displaystyle {\mathrm{}}_n}$) ${\displaystyle \ker(\reason _{n}})$의 정상적인 하위 그룹이다$.$ 그러면 인용 부문을 만들 수 있다.

${\displaystyle H_{n}(X):=\ker(\partial _{n}/\mathrm {im})(\partial _{n+1}=Z_{n}(X)/B_{n}(X),}$

X의 n번째 호몰로지 그룹이라고 불린다. H_n(X)의 원소를 호몰로지 클래스라고 한다. 각 호몰로지 클래스는 사이클에 걸친 동등성 클래스로, 동일한 호몰로지 클래스에 속하는 두 사이클은 호몰로직이라고 한다.^[19]

체인 콤플렉스는 (n+1)번째 맵의 이미지가 항상 n번째 맵의 커널과 같다면 정확하다고 한다. 따라서 X의 호몰로지 집단은 X와 관련된 연쇄 복합체가 정확하지 않은 "얼마나 먼"지를 측정한다.^[20]

체인 복합체 C(X)의 감소된 호몰로지 그룹은 증강 체인 복합체의^[21] 호몰로지로서 정의된다.

${\displaystyle \dotsb {\overset {\partial _{n+1}}{\longrightarrow \,}}C_{n}{\overset {\partial _{n}}{\longrightarrow \,}}C_{n-1}{\overset {\partial _{n-1}}{\longrightarrow \,}}\dotsb {\overset {\partial _{2}}{\longrightarrow \,}}C_{1}{\overset {\partial _{1}}{\longrightarrow \,}}C_{0}{\overset {\epsilon }{\longrightarrow \,}}\mathbb {Z} {\longright화살표 \,}0}$

여기서 경계 연산자 $ϵ{\displaystyle }$ ${\displaystyle \epsilon }$은(는)

${\displaystyle \epsilon \left(\sum _{i}n_{i}}}\ima _{i}\right)=\sum _{i}n_{i}}}}}}$

C의₀ 고정 생성기인$$ $\sum {\displaystyle }$${\displaystyle n_{}}$ i $,$ ${\displaystyle {}_{}{}_{}}$ , ${\displaystyle$ \$sum n_{i$}\$sigma$ _${i}$ 지점의 조합$$ ∑n ${\displaystyle i_{}}$${\displaystyle {}_{}}$, ${\displaystyle \sigma _{i}.$ The reduced homology groups ${\displaystyle {\tilde {H}}_{i}(X)}$ coincide with ${\displaystyle H_{i}(X)}$ for ${\displaystyle i\neq 0.}$ The extra ${\displaystyle \mathbb {Z} }$ in the chain complex represents the unique map ${\displaystyle [\emptyset ]\longrigh$$타로 X}$을(를) 빈 단순에서$$ X로 이동하십시오.

사이클 $Z{\displaystyle {}_{}}$ ${\displaystyle n_{}}$( ${\displaystyle X}$) ${\displaystyle Z_{n}($${\displaystyle X}$$)}$과 경계 $B{\displaystyle {}_{}}$ ${\displaystyle n_{}}$( X${\displaystyle }$) ${\displaystyle B_{n}(X)}$ 그룹을$$ 계산하는 것은 대개 매우 많은 수의 발전기를 가지고 있기 때문에 다소 어렵다. 반면에, 일을 더 쉽게 만드는 도구들이 있다.

단순 복합 X의 단순 호몰로지 그룹 H_n(X)는 단순 연쇄 복합체 C(X)를 사용하여 정의되며, C_n(X)는 X의 n-단순에 의해 생성된 자유 아벨리안 그룹과 함께 정의된다. 자세한 내용은 간단한 호몰로지를 참조하십시오.

단일 호몰로지 그룹 H_n(X)는 위상학적 공간 X에 대해 정의되며, 단순화 복합체에 대한 단순 호몰로지 그룹과 일치한다.

코호몰로지 그룹은 공식적으로 호몰로지 그룹과 유사하다. 하나는 체인 콤플렉스와 동일하지만 화살표는 n을 감소시키기보다는 n을 증가시키는 방향으로 ${\displaystyle d_{}}$, ${\displaystyle d_{n}}$을 나타내고, 그 다음 그룹 ${\displaystyle \ker }$ker${\displaystyle {}^{}}$(${\displaystyle d^{}}$) = ${\displaystyle Z^{}}$ n${\displaystyle {}^{}}$(${\displaystyle X}$ )$${\$displaysty \ker \left$.$(d^{n}\right)=Z^{$$n{\displaystyle \mathrm{}{\}(}^{}\mathrm{X}}$$)}$의 코코클과 i m${\displaystyle (\mathrm{dn}{}^{}}$-${\displaystyle }$1 ) = ${\displaystyle {}^{}}$ ${\displaystyle n^{}}$ X${\displaystyle }$) ${\displaystyle \matrm$ {$im} \left(d$^{$n-1}\right)=$$B^{n}(X)}$의 공동 경계는 동일한 설명에서 따른다. X의 n번째 코호몰로지 그룹은 그 다음 지수 그룹이다.

${\displaystyle H^{n}(X)=Z^{n}(X)/B^{n}(X),}$

n번째 호몰로지 그룹과 유사하게

호몰로지 vs. 호모토피

호모토피 집단은 위상학 공간에서 '구멍'을 나타낼 수 있다는 점에서 호몰로지 집단과 유사하다. 첫 번째 호모토피 그룹 $\pi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$(${\displaystyle X}$ ) ${\displaystyle \pi _{1}(X)}$과 첫 번째 호몰로지 그룹 ${\displaystyle {H\mathrm{}}_{}}$ $1{\displaystyle {}_{}}$( ${\displaystyle X}$) ${\displaysty H_{1}(X)$ 사이에 밀접한 관계가 있다 :$$후자는 전자의 아벨리안화다. 따라서, "호모학은 호모토피에 대한 상호 교환적인 대안"이라고 한다.^{[22]: 4:00} 더 높은 호모토피 그룹은 아벨리안이며 후레위츠 정리에 의한 호몰로지 그룹과 관련이 있지만 훨씬 더 복잡할 수 있다. 예를 들어, 구들의 호모토피 그룹은 잘 이해되지 않고 일반적으로 알려져 있지 않다. 호몰로지 그룹에 대해 위에서 설명한 것과 대조적이다.

예를 들어, X를 그림 8이 되게 하라. 첫 번째 호모토피 그룹 ${\displaystyle {\pi \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$( ${\displaystyle X}$) ${\displaystyle \pi _{1}(X)}$은 미리 정해진 지점(예: 중심)에서 시작하고 끝나는 방향 루프 그룹이다$$. 가장 왼쪽 사이클을 중심으로 루핑한 다음 가장 오른쪽 사이클을 중심으로 루핑한 다음 가장 왼쪽 사이클을 중심으로 루핑하는 것과 가장 왼쪽 사이클을 중심으로 루핑하는 것이 다른 2등급 자유 그룹에 해당한다. 대조적으로, 그것의 첫 번째 호몰로지 그룹 H ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle X}$) ${\displaystyle H_{1}(X)}$은 표면에서 만들어진 절단들의 그룹이다. 이 그룹은 (비공식적으로) 가장 왼쪽의 사이클을 자른 다음 가장 오른쪽 사이클을 자른 다음 가장 왼쪽 사이클을 자른 것과 같은 결과를 초래하기 때문에 가장 일치한다.

호몰로지 유형

서로 다른 형태의 동음이의 이론은 다양한 범주의 수학 객체에서 체인 복합체 범주에 이르는 functors 매핑에서 비롯된다. 각각의 경우에서 사물에서 체인 콤플렉스로, 그리고 체인 콤플렉스에서 호몰로지 그룹까지의 펑터의 구성은 이론에 대한 전체적인 호몰로지 펑터를 정의한다.^[23]

단순 호몰로지

동기부여의 예는 대수적 토폴로지: 단순 복합체 X의 단순 동질론에서 온다. 여기서 체인 그룹 C는_n 발전기가 X의 n차원 지향 심플렉스인 자유 아벨리아 그룹 또는 모듈이다. 그 배향과 이의 vertices의 n-tuple(σ[0],σ[1],…,σ[n]){\displaystyle(,\sigma[n]\sigma[0],\sigma[1],\dots)}오름차순에 나열된 지향적인 심플렉스 σ{\displaystyle \sigma}(즉 σ[0]<>σ[1]<>⋯<>σ[n]{\disp을 표명하는 단지의 vertices 명령에 의해 캡처됩니다.laystyle$\chma [0]<\cdots <\$cdots ${\displaystyle <\backslash }$cdma[$n]})$ 콤플렉스의 꼭지점 순서에 $따라$ $\cdots$ <\$cdma[n$]}이(가$)$ 튜플에 나타나는 $i{\displaystyle }$ ${\displaysty i}$의 꼭지점이다$$. C에서_n C로_n−1 $\partial {\displaystyle {\mathrm{}}_n}$ ${\$ 매핑을 경계 매핑이라고 하며 심플렉스 전송

${\displaystyle \sigma =(\displaystyle \sigma [0],\sigma [1],\],ma [n])}$

형식상으로는

${\displaystyle \n(\displaystyle \n}=\sum _{i=0}-1)^{i}\i}\liftma[0],\ftma[n-1],\ftma[i+1],\ftimema[n]\rigma],},}$

$n{\displaystyle }$= ${\displaystyle 0.}$ ${\displaystyle n=0.}$ 발전기의 이$$ 동작은 다음과 같이 모든 C에_n 동형성을 유도한다. 요소 c∈ Cn{\displaystylec\in C_{n}}을 감안할 때 발전기의 합으로 c)이 그것을 쓰∑ σ 나는 ∈ Xnm나는 σ 나는,{\textstyle c=\sum_{\sigma_{나는}\in X_{n}}m_{나는}\sigma _{나는},}여기서 Xn{\displaystyle X_{n}}집합의 n-simplexes에 X와 mi이 계수에서 반지를 Consols정리 공채. 정의. (달리 명시되지 않는 한 일반적으로 정수). 그런 다음 정의하십시오.

${\displaystyle \partial _{n}(c)=\sum _{\sigma _{n}\in X_{n}}\partial _{n}(\sigma _{i}).}$

X의 n번째 호몰로지 치수는 치수 n에서 X에 있는 "구멍"의 숫자임이 밝혀졌다. 이러한 경계 매핑의 행렬 표현을 Smith 일반 형식으로 입력하여 계산할 수 있다.

단수 호몰로지

단순한 호몰로지 예를 모델로 삼아 어떤 위상학적 공간 X에 대해서도 단일한 호몰로지(homology)를 정의할 수 있다. X를 위한 체인 콤플렉스는 C를_n 자유 아벨리아 그룹(또는 자유 모듈)으로 가져가는 것으로 정의된다. 이 그룹의 발전기는 모두 n차원 단순화에서 X로 이어지는 연속적인 맵이다. 동형체 ∂_n은 단순체의 경계 지도에서 비롯된다.

집단 호몰로지

추상대수학에서는 동음이의학을 사용하여 파생된 펑터(예: 토르 펑터)를 정의한다. 여기에서는 공변량 첨가 펑터 F와 일부 모듈 X로 시작한다. X에 대한 체인 콤플렉스는 다음과 같이 정의된다: 먼저 자유 모듈 ${\displaystyle {F\mathrm{}}_{}}$ ${\$}과$$ ${\displaystyle \mathrm{과부하}}$ 동형체 $p{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$: ${\displaystyle {F\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$→ X${\displaystyle }$. ${\displaystyp p_{1}:$$F_{1}\to X.}$ 그러면$$ $자유모듈{\displaystyle {}_{}}$ ${\displaystyle {F\mathrm{}}_{}}$2 {\$displaystyle F_{2$}}개$$$,$ 그리고 덧없는 동형상 $p{\displaystyle {}_{}}$ 2${\displaystyle {}_{}}$: ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$→ ${\displaystyle \ker }$ ${\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$)${\displaystyle }$. ${\displaystyp p_{2}:$$F_{2}\to \ker로 \left(p_{1}\right).$$}}$ 이런 식으로 계속하여$$ 자유모듈 $F{\displaystyle {}_{}}$ {${\displaystyle n_{}}$ ${\$와 동형동체 $p{\displaystyle {}_{}}$ ${\$의 순서를 정의할$$ 수 있다. Functor F를 이 시퀀스에 적용함으로써 체인 콤플렉스를 얻는다; 이 콤플렉스의$$ 호몰로지 ${\displaystyle H_{}}$ $n{\displaystyle {}_{}}$ ${\$는 F와 X에만 의존하며, 정의상 F의 n번째 파생 펑터는 X에 적용된다.

그룹 (co)호몰로지 $H{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$( ${\displaystyle G}$, $){\displaystyle H^{2}(G,M)}$의 일반적인 용도는 $G{\displaystyle }$ = E${\displaystyle }$/ ${\displaystyle M}$ . {\$displaystyle G=E/M}$을(를$)$ 포함하는 가능한 확장 그룹 E를 일반 하위 그룹으로 분류하는 것이다$$.

기타 호몰로지 이론

호몰로지 펑커스

체인 콤플렉스는 범주를 형성한다: 체인 콤플렉스의 형태론(${\displaystyle {}_{}}$ n${\displaystyle {}_{}}$→${\displaystyle {}_{}{A}_{}{}_{}}$n - ${\displaystyle 1_{}}$ ${\$$A_{n}\to A_{n-1$ 체인 복합체(${\displaystyle {}_{}}$ ${\displaystyle n_{}}$: B ${\displaystyle n_{}}$→ B${\displaystyle {}_{}}$- ${\displaystyle 1_{}}$ ${\$$B_{n}\to B_{n-1}$)는 동형상 $f{\displaystyle {}_{}}$: ${\displaystyle A_{}}$ ${\displaystyle n_{}}$→ ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$의 순서다.$A_{n}\to B_{n}}$에 대해 모든 ${\displaystyle n_{}}$에 $대해{\displaystyle {}_{}}$f - ${\displaystyle 1_{}{d}_{}}$d = ${\displaystyle e_{}{f}_{}}$ f ${\$ n-th homology H는_n 체인 콤플렉스의 범주에서 아벨리아 그룹(또는 모듈)의 범주까지 공변량 펑터로 볼 수 있다.

만일 체인 콤플렉스가 공변량 방식으로 객체 X에 의존한다면(어떤 형태론 $X{\displaystyle }$→ ${\displaystyle Y}$ ${\displaystyle$ X$\to$ Y$}$가 X의 체인 콤플렉스에서 Y의 체인 콤플렉스로 형태주의를 유도한다는$$ 의미), H는_n X가 아벨리아 그룹(또는 모듈)의 범주에 속하는 범주에서 공변량 펑커다.

상동과 cohomology의 유일한 차이는 cohomology으로 단지들은 반변 방식으로 X에서, 따라서 상동 단체들은 범주에서 X에abelian 그룹이나 modu의 범주에 속하형태 반변 functors(는cohomology 단체들이 이 컨텍스트에 표시된 Hn을 부르면)의지하고 있다.les

특성.

$($${\displaystyle {}_{}}$ ${\displaystyle n_{}}$: ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$→ A ${\displaystyle {\mathrm{n}}_{}}$- 1 ${\$}):$A_{n}\to A_{n-1$는 체인 콤플렉스로서, 미세하게 많은 A가_n 0이고, 다른 것들은 미세하게 생성된 아벨 그룹(또는 유한 차원 벡터 공간)이며, 그러면 오일러 특성을 정의할 수 있다.

${\displaystyle \chi =\sum(-1)^{n}\,\mathrm {rank}(A_{n})}$

(아벨리아 집단의 경우 순위 사용, 벡터 공간의 경우 하멜 치수 사용). 오일러 특성은 호몰로지 수준에서도 계산할 수 있는 것으로 나타났다.

${\displaystyle \chi =\sum(-1)^{n}\,\mathrm {rank}(H_{n})}$

그리고, 특히 대수적 위상에서, 이것은 체인 콤플렉스를 발생시킨 객체 X에 대한$$ 중요한 불변성 ${\displaystyle \chi }$을 계산하는 두 가지 방법을 제공한다.

모든 짧은 순서가 정확하다.

$A\오른쪽 화살표 B\오른쪽 화살표 C\오른쪽 화살표 0}$

연쇄 복합체들은 길고 정확한 일련의 동종학 집단들을 낳는다.

${\displaystyle \cdots \to H_{n}(A)\to H_{n}(B)\to H_{n}(C)\to H_{n-1}(A)\to H_{n-1}(B)\to H_{n-1}(C)\to H_{n-2}(A)\to \cdots }$

이 긴 정확한 순서의 모든 지도는 지도 H ${\displaystyle n_{}}$( C${\displaystyle }$)${\displaystyle }$→ ${\displaystyle H_{}}$ ${\displaystyle {}_{}}$- ${\displaystyle 1{}_{}}$( A )${\디스플레이스타일 H_{n}(C)\to H_{n-1(A)}$을 제외한 체인 단지들 간의 지도에 의해 유도되며, 후자를$$ 호모피즘 연결이라고 하며 지그재그 보조기(zig-zag)가 제공한다. 이 보조정리기는 상대적 호몰로지 이론과 메이어-베토리스 시퀀스 이론과 같이 호몰로지 집단을 계산하는 데 도움이 되는 여러 가지 방법으로 호몰로지에도 적용될 수 있다.

적용들

순수 수학에서의 응용

동질학을 사용하여 입증된 주목할 만한 이론은 다음과 같다.

• 브루워 고정 포인트 정리: 만약 f가 B구로부터ⁿ 그 자체로 이어지는 어떤 연속 ${\displaystyle \mathrm{지도}}$라면${\displaystyle ,}$ $f{\displaystyle }$ (${\displaystyle }$)${\displaystyle }$= . .${\displaystyle$a\$in B$$^{n$$}}$가 있는 고정$$ 지점이 있다$.$$}$
• 도메인 침입: U가 $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$ 및$$ $f{\displaystyle }$: ${\displaystyle U}$→ ${\displaystyle {}^{}}$ ${\displaystyle {\mathbb{}}^{}}$ ${\$$U\to \mathb{R} ^{n}}$는 주입식 연속 맵이고, $V{\displaystyle }$= f${\displaystyle (U}$) ${\displaystyle V=f(U)}$가 열려$$ 있고, f는 U와 V 사이의 동형성이다.
• 털복숭이 공 정리: 2-sphere(또는 더 일반적으로, ${\displaystyle \mathrm{어떤}}$ $k{\displaystyle }${$$1 {\$displaystyle k\geq$ 1$\}$에 대한 2k-sphere의 벡터 필드는 어느 시점에서 사라진다.
• 더 보르수크-울람 정리: n-sphere에서 유클리드 n-space에 이르는 모든 연속적인 함수는 몇 쌍의 항정신병 지점을 같은 지점에 매핑한다.(구상의 두 지점이 구 중심과 정확히 반대 방향에 있다면 항정신병이라고 한다.)
• 차원 침입: 비어 있지 않은 $오픈{\displaystyle }$ 서브셋 U ${\displaystyle \subseteq }$ ${\displaystyle {}^{}}$ ${\displaystyle {\mathbb{}}^{}}$ ${\$ {$R}$^{$m}}$ $및$ V ${\displaystyle \subseteq }$ ${\displaystyle {}^{}}$ n$${\$displaystyle$ $V\subseteq \$$mattb$ {$R}$$^{$$n$$}}}}}}$이 동형인 $경우$ m${\displaystyle }$= $.$$}$^[24]

이공계 지원

위상학적 데이터 분석에서 데이터 세트는 유클리드 공간에 내장된 다지관 또는 대수적 다양성의 점 구름 표본으로 간주된다. 클라우드에서 가장 가까운 인접 지점을 삼각측량 방식으로 연결하면 다지관의 단순 근사치가 생성되고 그 단순화된 호몰로지(homology)를 계산할 수 있다. 다중 길이 척도에 걸쳐 다양한 삼각측량 전략을 사용하여 동질학을 강력하게 계산할 수 있는 기법을 찾는 것이 지속적인 동질학의 주제다.^[25]

센서 네트워크에서 센서는 시간에 따라 동적으로 변화하는 애드호크 네트워크를 통해 정보를 전달할 수 있다. 이 일련의 로컬 측정 및 통신 경로의 글로벌 컨텍스트를 이해하려면 네트워크 토폴로지의 동질성을 계산하여 예를 들어 커버리지의 구멍 등을 평가하는 것이 유용하다.^[26]

물리학에서 역동적인 시스템 이론에서 푸앵카레는 역동적인 시스템의 불변 다지관과 그 위상적 불변성 사이의 상호작용을 가장 먼저 고려한 사람 중 한 명이었다. 모스 이론은 다지관의 구배 흐름의 역학을 예를 들어 그것의 동질성과 연관시킨다. 플로어 호몰로지(Floer homology)는 이것을 무한 차원 다지관으로 확장시켰다. KAM 정리는 주기적인 궤도를 복잡한 궤도를 따를 수 있다는 것을 확립했다; 특히 그들은 플로어 호몰로학을 이용하여 조사할 수 있는 땋은 모양을 형성할 수 있다.^[27]

유한 요소 방법의 한 종류에서, Hodge-Laplace 연산자와 관련된 미분방정식에 대한 경계-값 문제는 예를 들어 전자기 시뮬레이션에서 위상학적으로 비경쟁 영역에서 해결되어야 할 수 있다. 이러한 시뮬레이션에서, 솔루션은 선택된 경계 조건과 도메인의 호몰로지(homology)에 근거한 솔루션의 코호몰로지 클래스를 고정함으로써 도움을 받는다. FEM 도메인을 삼각측량할 수 있으며, 여기에서 단순 호몰로지를 계산할 수 있다.^[28][29]

소프트웨어

유한 세포 복합체의 호몰로지 그룹을 계산하기 위한 목적으로 다양한 소프트웨어 패키지가 개발되었다. Linbox는 Gap과 Maple 양쪽에 모두 접속하여 Smith 정상 형태를 포함한 빠른 매트릭스 작업을 수행하기 위한 C++ 라이브러리다. Chomp, CAPD::Redhom과 Perseus도 C++로 쓰여 있다. 세 가지 모두 매트릭스 대수학에 의존하기 전에 입력 셀 콤플렉스의 동질성 및 이산 모스 이론에 근거한 사전 처리 알고리즘을 구현한다. Kenzo는 Lisp로 쓰여져 있으며, 호몰로지 외에도 유한한 단순화 콤플렉스의 호모토피 그룹 프리젠테이션을 생성하는 데도 사용될 수 있다. Gmsh는 유한 요소 메시에 대한 호몰로지 해결사를 포함하며, 유한 요소 소프트웨어에서 직접 사용할 수 있는 코호몰로지 기반을 생성할 수 있다.^[28]

참고 항목

• 베티 수
• 사이클 스페이스
• 드 람 코호몰로지
• 에일렌베르크-스텐로드 공리
• 비상식적 호몰로지론
• 호몰로지 대수
• 정류대수의 동질적 추측
• 동질적 연결성
• 동질 차원
• 호모토피군
• 귄네스 정리
• 코호몰로지 이론 목록 - 호몰로지 이론 목록도 있음
• 푸앵카레 이중성

메모들

참조

• Cartan, Henri Paul; Eilenberg, Samuel (1956). Homological Algebra. Princeton mathematical series. Vol. 19. Princeton University Press. ISBN 9780674079779. OCLC 529171.
• Eilenberg, Samuel; Moore, J.C. (1965). Foundations of relative homological algebra. Memoirs of the American Mathematical Society number. Vol. 55. American Mathematical Society. ISBN 9780821812556. OCLC 1361982.
• Gowers, Timothy; Barrow-Green, June; Leader, Imre, eds. (2010), The Princeton Companion to Mathematics, Princeton University Press, ISBN 9781400830398.
• Hatcher, A. (2002), Algebraic Topology, Cambridge University Press, ISBN 0-521-79540-0. 단순화 복합체 및 다지관, 단일한 호몰로지 등에 대한 호몰로지 이론에 대한 자세한 논의
• Hilton, Peter (1988), "A Brief, Subjective History of Homology and Homotopy Theory in This Century", Mathematics Magazine, Mathematical Association of America, 60 (5): 282–291, doi:10.1080/0025570X.1988.11977391, JSTOR 2689545
• Richeson, D. (2008), Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton University.
• Spanier, Edwin H. (1966), Algebraic Topology, Springer, p. 155, ISBN 0-387-90646-0.
• Stillwell, John (1993), Classical Topology and Combinatorial Group Theory, Springer, doi:10.1007/978-1-4612-4372-4_6, ISBN 978-0-387-97970-0.
• Teicher, M., ed. (1999), The Heritage of Emmy Noether, Israel Mathematical Conference Proceedings, Bar-Ilan University/American Mathematical Society/Oxford University Press, ISBN 978-0-19-851045-1, OCLC 223099225
• Weibel, Charles A. (1999), "28. History of Homological Algebra" (PDF), in James, I. M. (ed.), History of Topology, Elsevier, ISBN 9780080534077.

외부 링크

• 수학 백과사전 호몰로지 그룹