타원
Ellipse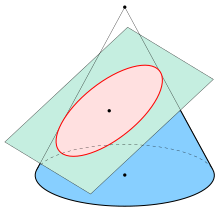
수학에서 타원은 두 개의 초점을 둘러싼 평면 곡선으로, 곡선의 모든 점에 대해 두 개의 초점까지의 거리의 합이 상수입니다.이렇게 두 초점이 같은 타원의 특수한 형태인 원을 일반화한다.타원의 신장은 e(\로 측정되며, 은 e 0(의 한계치)부터 1 이상 이 아닌 포물선)까지의 수치입니다.
타원은 면적에 대한 단순한 대수적 해법을 가지지만, 정확한 해법을 얻기 위해 적분이 필요한 주변(원주라고도 함)에 대한 근사치만 가지고 있다.
해석적으로 폭 의 원점을 중심으로 한 표준 타원의 방정식은 다음과 같습니다.
a b라고 하면 는c - btextstyle c- b입니다.표준 파라미터 방정식은 다음과 같습니다.
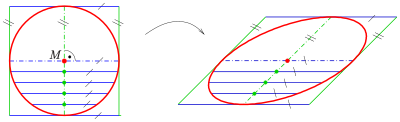
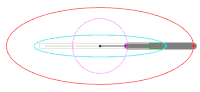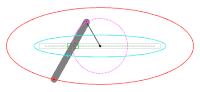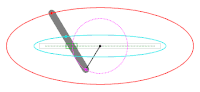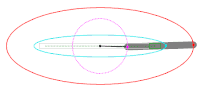
타원형은 원뿔 단면의 닫힌 유형입니다. 원뿔과 평면의 교점을 추적하는 평면 곡선입니다(그림 참조).타원형은 다른 두 형태의 원뿔 단면인 포물선과 쌍곡선과 많은 유사점을 가지고 있는데, 둘 다 개방적이고 무한하다.원통의 각진 단면도 타원이다.
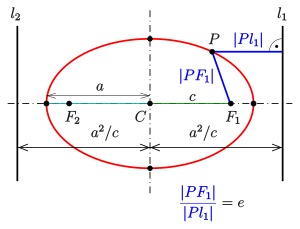
타원은 또한 하나의 초점과 직각이라고 불리는 타원 밖의 선으로 정의될 수 있습니다. 즉, 타원상의 모든 점에 대해 초점에 대한 거리와 직각점에 대한 거리 사이의 비율은 상수입니다.이 일정한 비율은 위에서 설명한 편심률입니다.
타원은 물리학, 천문학, 공학에서 흔히 볼 수 있다.예를 들어, 태양계에 있는 각 행성의 궤도는 태양이 한 초점에 있는 대략 타원형입니다(더 정확히 말하면, 초점은 태양-행성 쌍의 중심입니다).행성 주위를 도는 위성과 두 개의 천체가 있는 다른 모든 시스템에 대해서도 마찬가지다.행성과 별의 모양은 종종 타원체에 의해 잘 묘사된다.측면 각도에서 보는 원은 타원처럼 보입니다. 즉, 타원은 평행 또는 투시 투영 중인 원의 이미지입니다.타원은 또한 수평과 수직 운동이 같은 주파수를 가진 사인파일 때 형성되는 가장 단순한 리사주 도형입니다. 비슷한 효과는 광학에서 빛의 타원 편광으로 이어집니다.
이 이름은 페르가의 아폴로니오스가 코닉스에서 붙인 이름이다.
점의 궤적으로 정의
타원은 유클리드 평면에서 점의 집합 또는 궤적으로 기하학적으로 정의할 수 있습니다.
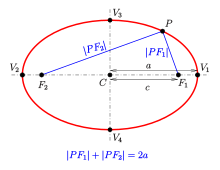
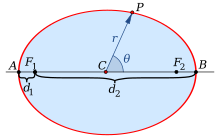
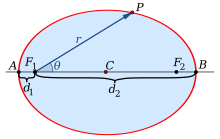
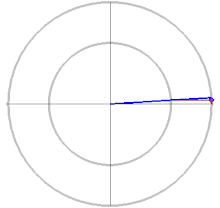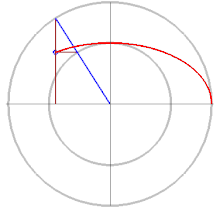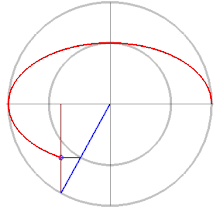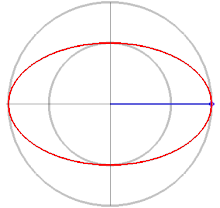
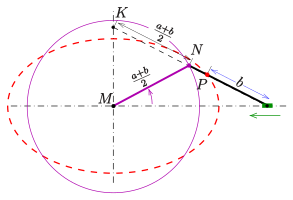
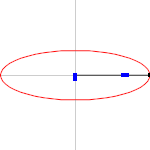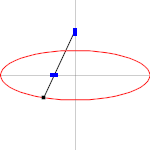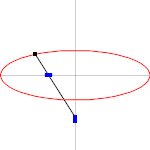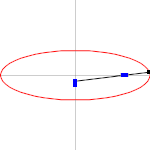
- 2개의 와 거리 ({가 Fci 사이의 거리보다 클 경우 타원은 점({P})의 집합으로, style P})의 합계가 됩니다.는 2 {\ : { R F + 입니다 \ E = \ \ { }
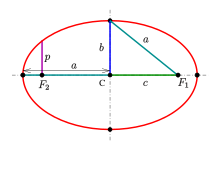
Foci를 연결하는 선분의 C C를 타원의 중심이라고 합니다.Foci를 통과하는 선을 장축이라고 하며, 중심을 통과하는 선에 수직인 선을 단축이라고 합니다.장축은 갖는 두 의 1, V_{1}, V_에서 타원과 교차합니다.중심까지의 Foci cc를 초점 거리 또는 선형 편심이라고 합니다. a{\ e의 몫은 편심률입니다.
}=는 원을 생성하며 특수한 유형의 타원에 포함된다.
P + 1 a (\{2}} =는 다른 방식으로 볼 수 있습니다(그림 참조).
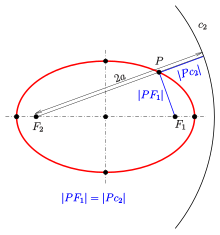
- 2가 이고 중심 ({2a})인 점({P})에서 까지의 거리는 까지의 거리입니다.
2는 [1][2]타원의 원형 다이렉트릭스( 라고 불립니다.이 속성은 아래의 직행렬 선을 사용하는 타원의 정의와 혼동해서는 안 됩니다.
단델린 구를 사용하면 평면이 정점을 포함하지 않고 원뿔의 선보다 경사가 작다고 가정할 때 평면이 있는 원뿔의 모든 부분이 타원임을 증명할 수 있다.
데카르트 좌표
표준 방정식
데카르트 좌표에서 타원의 표준 형식은 원점이 타원의 중심이고 x축이 장축이며 다음과 같이 가정합니다.
- foci는 ( ,), ( - , F_}= (, ),\ }= 0
- 정점은 V ( ,), ( - , }=(}=입니다.
임의의 점 의 경우displaystyle)}, 포커스까지의 거리( (는 (x + y2({)^2})입니다. 및다른 + ) + y 2 + } + y^{} 점y x,))은 다음과 같은 경우 항상 타원상에 있습니다.
적절한 사각형으로 라디칼을 제거하고 - ({ b}=를 하면 [3]타원의 표준 방정식이 생성된다.
또는 y에 대해 해결:
폭 및 높이 a a를 준장축 및 반단축이라고 합니다.상단 및 하단 V (0 ,), (, -) { V_}= (, b ) , \ ; }= (0, b )}는 공칭입니다.타원의 점 에서 좌우 foci까지의 거리(는+ (\ a a - (\ style 입니다.
이는 타원이 좌표축에 대해 대칭이며, 따라서 원점에 대해 대칭이라는 방정식에서 비롯됩니다.
파라미터
주축
이 문서 전체에서 준장축과반장축은 각각\와 b\b로 됩니다., \ a \ b \}
원칙적으로 a + 1 {\}} { + {\ {}} }은<b {따라서 타원은 넓이보다 크다)를 수 있다.이 폼은 변수 x x ydisplaystyle b를 으로써 표준 으로 변환할 수 있습니다.
선형 편심
이것은 중심에서 초점까지의 거리입니다.c - (\ c =
편심
편심도는 다음과 같이 나타낼 수 있습니다.
a>. \ a 를 로 합니다.} 등축 ( a \ b )은 편심률이 0이며 원이다
반라투스 직장
장축에 수직인 하나의 초점을 통과하는 현의 길이를 라투스 직장이라고 합니다.그 중 절반은 과 같습니다.
는 정점에서의 곡률반경과 동일합니다(섹션 곡률 참조).
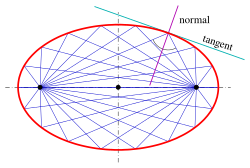
접선
임의의 g(\ g는 각각 외부 선, 접선 및 분할선이라고 하는 0, 1 또는 2 지점에서 타원과 교차합니다.타원의 어떤 점을 통해서도 독특한 접선이 있다. a + b {\ { + {\ {}} 1의점( 에서의 탄젠트에는 다음과 같은 좌표가 있습니다.
접선의 벡터 모수 방정식은 다음과 같습니다.
- ( 1) +( - b ){ {{x } \ \ \ \ y _ {} + { } \ ; \ ; - _ {^ { 2 \
증명: ( 1, ){ { ( y 1)+ ( v) { { { } x { \ \ \ \ \ } \ pmv } 。 x, ){ 타원 방정식에 선 방정식을 하고 2 + b 1 { displaystyle {} { + {1} = {b1} =} {2} {b1} } } }
예를 들어 다음과 같은 경우가 있습니다.
- } 선(\g)와 타원에는 y11},1})만 있고(\g)는 접선입니다의 접선 방향{\frac{y_{1}}{b^{2}}}\end{pmatrix}}}, 그래서 접선의 라인 12x+y1b2y)k{\textstyle{\frac{x_{1}}{a^{2}}}x+{\tfrac{y_{1}}x 방정식이 수직 벡터(x12y1b2){\displaystyle{\begin{pmatrix}{\frac{x_{1}}{a^{2}}}및 가지고 있다.{b^k에 {2}} (1, y){은 접선 및 타원상에 있으므로k k이 됩니다
- 1 u + 2 {{}}{}}{b2}} 0타원과 공통되는 두 번째 점을 가지며 두 번째 경계입니다.
(1)을 사용하면 (- 2 2 }-1}가에서의 탄젠트 벡터이며 이는 벡터 을 증명한다.
1, ) { } 및 (,v) { ) { \ x {a^ { + {\ {v} { 등 의 두 점일 경우(a 인 ({ a 타원은 원이고 "직교"는 "직교"를 의미합니다.)
어긋난 타원
표준 타원이 중심 , 을 가지도록 이동하면(\displaystyle } ,,}\ 방정식은 다음과 같습니다.
축은 여전히 x축과 y축과 평행합니다.
일반 타원
해석기하학에서 타원은 사각형으로 정의된다: 데카르트 평면의점 집합 ( {{ ( Y은 퇴화되지 않은 경우 암묵적[5][6] 방정식을 충족한다.
2- 4 C < B< .
퇴행 케이스와 비퇴행 케이스를 구별하기 위해 be를 결정 인자로 한다.
그러면 타원은 Cθ < 0일 때에만 퇴화하지 않는 실제 타원이 됩니다. Cθ > 0일 때 우리는 가상의 타원이며, θ = 0일 때 우리는 점 [7]: p.63 타원이 됩니다.
일반 방정식의 계수는 알려진 반장축(\ a b(\ b 중심좌표,, },및 양식 \displaystyle \에서 구할 수 있습니다.타원의 장축에 대한 탈 축)의 경우 다음 공식을 사용합니다.
이러한 식은 좌표 )의 아핀 변환을 표준 x + 2 { { + {\ 에서 도출할 수 있습니다.
반대로 표준 폼 파라미터는 다음 방정식에 의해 일반 폼계수로부터 얻을 수 있습니다.
파라메트릭 표현
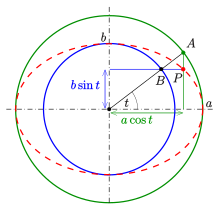
표준 파라메트릭 표현
삼각 함수를 사용하여 표준 a + 2 { + {\ {}}=의 파라메트릭 표현은 다음과 같습니다.
파라미터 t(천문학에서는 편심 이상이라고 부릅니다)는 x축과의 ( ) , (){style ( (의각도가 아니지만 Philippe de La Hire([8]아래 그림 생략 부호 참조)로 인해 기하학적 의미가 있습니다.
합리적 표현
tan ( 2) { u= \ \{ { \ } 치환으로 공식은 구한다.
그리고 타원의 합리적 파라메트릭 방정식은
이 값은 왼쪽정점0)을 제외한 의 임의의 점 a + 2 2 {{}} + }} b^{2}}1} { = 1}을 포함합니다.
u [ , , {\u\[, 1} 의 , 이 공식은u.\u.} 의 반시계방향으로 이동하는 타원의 오른쪽 윗부분을 나타냅니다. 왼쪽 정점은 u ± ( () , ( ) ( - , ). { _}( ,)= 입니다.
또는 파라미터[: :}}{ 가 실제 P상의 점이라고 간주되는 경우, 대응하는 합리적 파라미터화는 다음과 같습니다.
다음으로[ - ,) .{ : ]\( - ,0 ) 。
원뿔 단면의 합리적 표현은 컴퓨터 보조 설계에서 일반적으로 사용됩니다(베지어 곡선 참조).
모수로서의 접선 기울기
타원점에서의 접선의 m(\ m을 이용한 파라메트릭 표현은 표준 x ( ) ( cost , sint ) { \ ( t ) = ( \ t , { math f 의 도함수로부터 얻을 수 있다.
삼각 공식을 사용하면 다음을 얻을 수 있습니다.
표준 표현의 cost \ \ t t를 치환하면 과 같은 결과가 나옵니다.
서m {\m은 해당 타원점에서의 접선의 이며, c + {\ {은 위쪽, -{\는 타원의 아래쪽입니다.수직 접선이 있는꼭지점 , style a은 이 표현에 포함되지 않습니다.
c ±( ) { _ { \ pm ( m ) 에서의 접선의 방정식은 x+ { \ yperm + 입니다.아직 않은 n n은(는) 대응하는 c ± ( {의 좌표를 삽입하여 확인할 수 있습니다.
타원의 접선에 대한 이러한 설명은 타원의 직각을 결정하는 데 필수적인 도구입니다.이 직교 기사는 미적분과 삼각 공식 없이 또 다른 증거를 포함하고 있다.
일반 타원
타원에 대한 또 다른 정의에서는 아핀 변환을 사용합니다.
- 모든 타원은 단위 원의 아핀 이미지이며 은 2+ 2 {\ x}=입니다
- 파라메트릭 표현
유클리드 평면의 아핀 은 x f + { style { {} \ ! { } + { \ {}。서 { A }는 정규 매트릭스이며 style{ _은(는) 임의 벡터입니다. 이면 f 스타일 는 A A의 열 벡터입니다.단위원cos( ) , sin , ( \ ( ) , \( t )} , 0 t 2{\ { \ 2 \ pi } is onto ontoipseipseipseipseipseipse 。
f 입니다.이(가) 이고 f→ ,f ({입니다!는 일반적으로 수직이 아닌 두 공역 직경의 방향이다.
- 꼭지점
타원의 4개의 꼭지점은 ( ) , ( 0 ± 2 ) , ( 0 + ) , ( ) , \ ; {\ \ ( \ { } \} , \ )
( f { { \ ) 。 으로 }=이것은 다음과 같이 도출됩니다. ( ) { 지점의 접선 벡터는 다음과 같습니다.
정점 t 0 {\ t에서 접선은 장축/장축에 수직입니다. 따라서 다음과 같습니다.
2t - 2 t t , sin t sin t 2 t \ = \ 2 t ; \ t \ cos 2 t =\ sin 2 \ t ;} 。
- 지역
아폴로니오스 정리(아래 참조)에서는 다음을 얻는다.
x + cost + → 2 sint t t { \ ; { \ {} = } _ { } + { \ { \ + { { f } { \ { f } \ \ sin ;} ;
- 세미악세스
M + , ( , f ){\ ; M={{ + {\{2}^2, \ N = \f} { {f} {f_1} { {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f} {f}}}} {f}} {
a에 이 비선형 시스템을 해결하면 다음과 같은 반각형이 생성됩니다.
- 암묵적 표현
cos t { \ ; \ t , \ t\ ; }의 파라메트릭 표현을 Cramer의 법칙으로 풀고 2 + 2 - 1 { \ ; \ ^ {+ \ 1 ; sin 을 하면 암묵적인 표현을 얻을 수 있다.
반대로, 방정식이
- 2 + x + 2 - , x 2} + 2 + 2 cxy + d^ {^ {2} - {2} \ , ,} (\ ; {2} - {> \; )
원점을 중심으로 한 타원의 두 벡터가 주어지고,
두 개의 공역점을 가리키며 위에서 개발한 도구를 적용할 수 있습니다.
예: + + y - 0 {\ }-10\;}인 타원의 경우, 벡터는 다음과 같다.
- ( ), ( - {{ { 1 } { 1 \ 0 } , \ { { 1 \ 1}
- Rotated Standard ellipse
For one obtains a parametric representation of the standard ellipse rotated by angle :
- Ellipse in space
The definition of an ellipse in this section gives a parametric representation of an arbitrary ellipse, even in space, if one allows to be vectors in space.
Polar forms
Polar form relative to center
In polar coordinates, with the origin at the center of the ellipse and with the angular coordinate measured from the major axis, the ellipse's equation is[7]: p. 75
Polar form relative to focus
If instead we use polar coordinates with the origin at one focus, with the angular coordinate still measured from the major axis, the ellipse's equation is
where the sign in the denominator is negative if the reference direction points towards the center (as illustrated on the right), and positive if that direction points away from the center.
In the slightly more general case of an ellipse with one focus at the origin and the other focus at angular coordinate , the polar form is
The angle in these formulas is called the true anomaly of the point. The numerator of these formulas is the semi-latus rectum .
Eccentricity and the directrix property
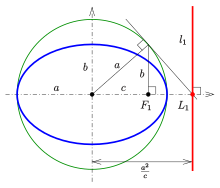
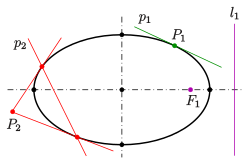
Each of the two lines parallel to the minor axis, and at a distance of from it, is called a directrix of the ellipse (see diagram).
- For an arbitrary point of the ellipse, the quotient of the distance to one focus and to the corresponding directrix (see diagram) is equal to the eccentricity:
The proof for the pair follows from the fact that and satisfy the equation
The second case is proven analogously.
The converse is also true and can be used to define an ellipse (in a manner similar to the definition of a parabola):
- For any point (focus), any line (directrix) not through , and any real number with the ellipse is the locus of points for which the quotient of the distances to the point and to the line is that is:
The extension to , which is the eccentricity of a circle, is not allowed in this context in the Euclidean plane. However, one may consider the directrix of a circle to be the line at infinity in the projective plane.
(The choice yields a parabola, and if , a hyperbola.)
- Proof
Let , and assume is a point on the curve. The directrix has equation . With , the relation produces the equations
- and
The substitution yields
This is the equation of an ellipse (), or a parabola (), or a hyperbola (). All of these non-degenerate conics have, in common, the origin as a vertex (see diagram).
If , introduce new parameters so that , and then the equation above becomes
which is the equation of an ellipse with center , the x-axis as major axis, and the major/minor semi axis .
- Construction of a directrix
Because of point of directrix (see diagram) and focus are inverse with respect to the circle inversion at circle (in diagram green). Hence can be constructed as shown in the diagram. Directrix is the perpendicular to the main axis at point .
- General ellipse
If the focus is and the directrix , one obtains the equation
(The right side of the equation uses the Hesse normal form of a line to calculate the distance .)
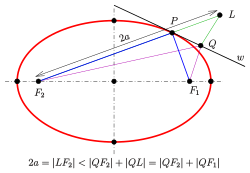
Focus-to-focus reflection property
An ellipse possesses the following property:
- The normal at a point bisects the angle between the lines .
- Proof
Because the tangent is perpendicular to the normal, the statement is true for the tangent and the supplementary angle of the angle between the lines to the foci (see diagram), too.
Let be the point on the line with the distance to the focus , is the semi-major axis of the ellipse. Let line be the bisector of the supplementary angle to the angle between the lines . In order to prove that is the tangent line at point , one checks that any point on line which is different from cannot be on the ellipse. Hence has only point in common with the ellipse and is, therefore, the tangent at point .
From the diagram and the triangle inequality one recognizes that holds, which means: . The equality is true from the Angle bisector theorem because and . But if is a point of the ellipse, the sum should be .
- Application
The rays from one focus are reflected by the ellipse to the second focus. This property has optical and acoustic applications similar to the reflective property of a parabola (see whispering gallery).
Conjugate diameters
Definition of conjugate diameters
A circle has the following property:
- The midpoints of parallel chords lie on a diameter.
An affine transformation preserves parallelism and midpoints of line segments, so this property is true for any ellipse. (Note that the parallel chords and the diameter are no longer orthogonal.)
- Definition
Two diameters of an ellipse are conjugate if the midpoints of chords parallel to lie on
From the diagram one finds:
- Two diameters of an ellipse are conjugate whenever the tangents at and are parallel to .
Conjugate diameters in an ellipse generalize orthogonal diameters in a circle.
In the parametric equation for a general ellipse given above,
any pair of points belong to a diameter, and the pair belong to its conjugate diameter.
For the common parametric representation of the ellipse with equation one gets: The points
- (signs: (+,+) or (-,-) )
- (signs: (-,+) or (+,-) )
- are conjugate and
In case of a circle the last equation collapses to
Theorem of Apollonios on conjugate diameters
For an ellipse with semi-axes the following is true:[9][10]
- Let and be halves of two conjugate diameters (see diagram) then
- .
- The triangle with sides (see diagram) has the constant area , which can be expressed by , too. is the altitude of point and the angle between the half diameters. Hence the area of the ellipse (see section metric properties) can be written as .
- The parallelogram of tangents adjacent to the given conjugate diameters has the
- Proof
Let the ellipse be in the canonical form with parametric equation
- .
The two points are on conjugate diameters (see previous section). From trigonometric formulae one obtains and
The area of the triangle generated by is
and from the diagram it can be seen that the area of the parallelogram is 8 times that of . Hence
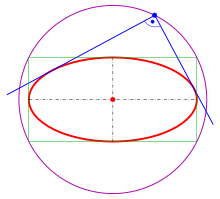
Orthogonal tangents
For the ellipse the intersection points of orthogonal tangents lie on the circle .
This circle is called orthoptic or director circle of the ellipse (not to be confused with the circular directrix defined above).
Drawing ellipses
Ellipses appear in descriptive geometry as images (parallel or central projection) of circles. There exist various tools to draw an ellipse. Computers provide the fastest and most accurate method for drawing an ellipse. However, technical tools (ellipsographs) to draw an ellipse without a computer exist. The principle of ellipsographs were known to Greek mathematicians such as Archimedes and Proklos.
If there is no ellipsograph available, one can draw an ellipse using an approximation by the four osculating circles at the vertices.
For any method described below, knowledge of the axes and the semi-axes is necessary (or equivalently: the foci and the semi-major axis). If this presumption is not fulfilled one has to know at least two conjugate diameters. With help of Rytz's construction the axes and semi-axes can be retrieved.
de La Hire's point construction
The following construction of single points of an ellipse is due to de La Hire.[11] It is based on the standard parametric representation of an ellipse:
- Draw the two circles centered at the center of the ellipse with radii and the axes of the ellipse.
- Draw a line through the center, which intersects the two circles at point and , respectively.
- Draw a line through that is parallel to the minor axis and a line through that is parallel to the major axis. These lines meet at an ellipse point (see diagram).
- Repeat steps (2) and (3) with different lines through the center.
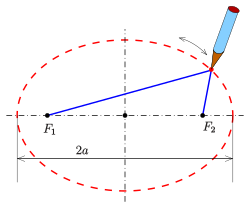
Pins-and-string method
The characterization of an ellipse as the locus of points so that sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points, which become the ellipse's foci. A string is tied at each end to the two pins; its length after tying is . The tip of the pencil then traces an ellipse if it is moved while keeping the string taut. Using two pegs and a rope, gardeners use this procedure to outline an elliptical flower bed—thus it is called the gardener's ellipse.
A similar method for drawing confocal ellipses with a closed string is due to the Irish bishop Charles Graves.
Paper strip methods
The two following methods rely on the parametric representation (see section parametric representation, above):
This representation can be modeled technically by two simple methods. In both cases center, the axes and semi axes have to be known.
- Method 1
The first method starts with
- a strip of paper of length .
The point, where the semi axes meet is marked by . If the strip slides with both ends on the axes of the desired ellipse, then point traces the ellipse. For the proof one shows that point has the parametric representation , where parameter is the angle of the slope of the paper strip.
A technical realization of the motion of the paper strip can be achieved by a Tusi couple (see animation). The device is able to draw any ellipse with a fixed sum , which is the radius of the large circle. This restriction may be a disadvantage in real life. More flexible is the second paper strip method.
A variation of the paper strip method 1 uses the observation that the midpoint of the paper strip is moving on the circle with center (of the ellipse) and radius . Hence, the paperstrip can be cut at point into halves, connected again by a joint at and the sliding end fixed at the center (see diagram). After this operation the movement of the unchanged half of the paperstrip is unchanged.[12] This variation requires only one sliding shoe.
- Method 2
The second method starts with
- a strip of paper of length .
One marks the point, which divides the strip into two substrips of length and . The strip is positioned onto the axes as described in the diagram. Then the free end of the strip traces an ellipse, while the strip is moved. For the proof, one recognizes that the tracing point can be described parametrically by , where parameter is the angle of slope of the paper strip.
This method is the base for several ellipsographs (see section below).
Similar to the variation of the paper strip method 1 a variation of the paper strip method 2 can be established (see diagram) by cutting the part between the axes into halves.
Trammel of Archimedes (principle)
Ellipsograph due to Benjamin Bramer
Most ellipsograph drafting instruments are based on the second paperstrip method.
Approximation by osculating circles
From Metric properties below, one obtains:
- The radius of curvature at the vertices is:
- The radius of curvature at the co-vertices is:
The diagram shows an easy way to find the centers of curvature at vertex and co-vertex , respectively:
- mark the auxiliary point and draw the line segment
- draw the line through , which is perpendicular to the line
- the intersection points of this line with the axes are the centers of the osculating circles.
(proof: simple calculation.)
The centers for the remaining vertices are found by symmetry.
With help of a French curve one draws a curve, which has smooth contact to the osculating circles.
Steiner generation
The following method to construct single points of an ellipse relies on the Steiner generation of a conic section:
- Given two pencils of lines at two points (all lines containing and , respectively) and a projective but not perspective mapping of onto , then the intersection points of corresponding lines form a non-degenerate projective conic section.
For the generation of points of the ellipse one uses the pencils at the vertices . Let be an upper co-vertex of the ellipse and .
is the center of the rectangle . The side of the rectangle is divided into n equal spaced line segments and this division is projected parallel with the diagonal as direction onto the line segment and assign the division as shown in the diagram. The parallel projection together with the reverse of the orientation is part of the projective mapping between the pencils at and needed. The intersection points of any two related lines and are points of the uniquely defined ellipse. With help of the points the points of the second quarter of the ellipse can be determined. Analogously one obtains the points of the lower half of the ellipse.
Steiner generation can also be defined for hyperbolas and parabolas. It is sometimes called a parallelogram method because one can use other points rather than the vertices, which starts with a parallelogram instead of a rectangle.
As hypotrochoid
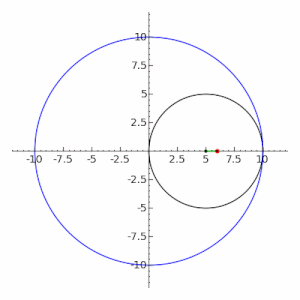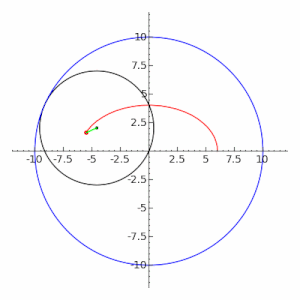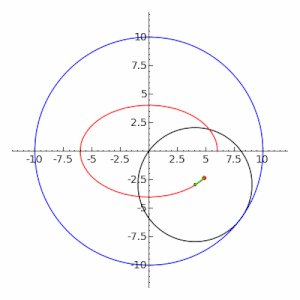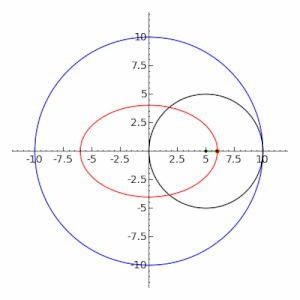
The ellipse is a special case of the hypotrochoid when , as shown in the adjacent image. The special case of a moving circle with radius inside a circle with radius is called a Tusi couple.
Inscribed angles and three-point form
Circles
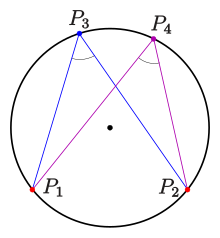
A circle with equation is uniquely determined by three points not on a line. A simple way to determine the parameters uses the inscribed angle theorem for circles:
- For four points (see diagram) the following statement is true:
- The four points are on a circle if and only if the angles at and are equal.
Usually one measures inscribed angles by a degree or radian θ, but here the following measurement is more convenient:
- In order to measure the angle between two lines with equations one uses the quotient:
Inscribed angle theorem for circles
For four points no three of them on a line, we have the following (see diagram):
- The four points are on a circle, if and only if the angles at and are equal. In terms of the angle measurement above, this means:
At first the measure is available only for chords not parallel to the y-axis, but the final formula works for any chord.
Three-point form of circle equation
- As a consequence, one obtains an equation for the circle determined by three non-colinear points :
For example, for the three-point equation is:
- , which can be rearranged to
Using vectors, dot products and determinants this formula can be arranged more clearly, letting :
The center of the circle satisfies:
The radius is the distance between any of the three points and the center.
Ellipses
This section, we consider the family of ellipses defined by equations with a fixed eccentricity . It is convenient to use the parameter:
and to write the ellipse equation as:
where q is fixed and vary over the real numbers. (Such ellipses have their axes parallel to the coordinate axes: if , the major axis is parallel to the x-axis; if , it is parallel to the y-axis.)
Like a circle, such an ellipse is determined by three points not on a line.
For this family of ellipses, one introduces the following q-analog angle measure, which is not a function of the usual angle measure θ:[13][14]
- In order to measure an angle between two lines with equations one uses the quotient:
Inscribed angle theorem for ellipses
- Given four points , no three of them on a line (see diagram).
- The four points are on an ellipse with equation if and only if the angles at and are equal in the sense of the measurement above—that is, if
At first the measure is available only for chords which are not parallel to the y-axis. But the final formula works for any chord. The proof follows from a straightforward calculation. For the direction of proof given that the points are on an ellipse, one can assume that the center of the ellipse is the origin.
Three-point form of ellipse equation
- A consequence, one obtains an equation for the ellipse determined by three non-colinear points :
For example, for and one obtains the three-point form
- and after conversion
Analogously to the circle case, the equation can be written more clearly using vectors:
where is the modified dot product
Pole-polar relation
Any ellipse can be described in a suitable coordinate system by an equation . The equation of the tangent at a point of the ellipse is If one allows point to be an arbitrary point different from the origin, then
- point is mapped onto the line , not through the center of the ellipse.
This relation between points and lines is a bijection.
The inverse function maps
- line onto the point and
- line onto the point
Such a relation between points and lines generated by a conic is called pole-polar relation or polarity. The pole is the point; the polar the line.
By calculation one can confirm the following properties of the pole-polar relation of the ellipse:
- For a point (pole) on the ellipse, the polar is the tangent at this point (see diagram: ).
- For a pole outside the ellipse, the intersection points of its polar with the ellipse are the tangency points of the two tangents passing (see diagram: ).
- For a point within the ellipse, the polar has no point with the ellipse in common (see diagram: ).
- The intersection point of two polars is the pole of the line through their poles.
- The foci and , respectively, and the directrices and , respectively, belong to pairs of pole and polar. Because they are even polar pairs with respect to the circle , the directrices can be constructed by compass and straightedge (see Inversive geometry).
Pole-polar relations exist for hyperbolas and parabolas as well.
Metric properties
All metric properties given below refer to an ellipse with equation
-
(1)
except for the section on the area enclosed by a tilted ellipse, where the generalized form of Eq.(1) will be given.
Area
The area enclosed by an ellipse is:
-
(2)
where and are the lengths of the semi-major and semi-minor axes, respectively. The area formula is intuitive: start with a circle of radius (so its area is ) and stretch it by a factor to make an ellipse. This scales the area by the same factor: [15] However, using the same approach for the circumference would be fallacious – compare the integrals and . It is also easy to rigorously prove the area formula using integration as follows. Equation (1) can be rewritten as For this curve is the top half of the ellipse. So twice the integral of over the interval will be the area of the ellipse:
The second integral is the area of a circle of radius that is, So
An ellipse defined implicitly by has area
The area can also be expressed in terms of eccentricity and the length of the semi-major axis as (obtained by solving for flattening, then computing the semi-minor axis).
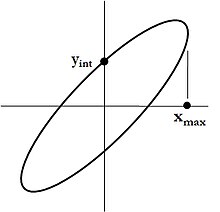
So far we have dealt with erect ellipses, whose major and minor axes are parallel to the and axes. However, some applications require tilted ellipses. In charged-particle beam optics, for instance, the enclosed area of an erect or tilted ellipse is an important property of the beam, its emittance. In this case a simple formula still applies, namely
-
(3)
where , are intercepts and , are maximum values. It follows directly from Apollonios's theorem.
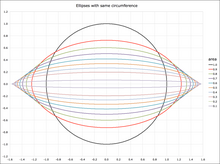
Circumference
The circumference of an ellipse is:
where again is the length of the semi-major axis, is the eccentricity, and the function is the complete elliptic integral of the second kind,
which is in general not an elementary function.
The circumference of the ellipse may be evaluated in terms of using Gauss's arithmetic-geometric mean;[16] this is a quadratically converging iterative method (see here for details).
The exact infinite series is:
where is the double factorial (extended to negative odd integers by the recurrence relation , for ). This series converges, but by expanding in terms of James Ivory[17] and Bessel[18] derived an expression that converges much more rapidly:
Srinivasa Ramanujan gave two close approximations for the circumference in §16 of "Modular Equations and Approximations to ";[19] they are
and
where takes on the same meaning as above. The errors in these approximations, which were obtained empirically, are of order and respectively.
Arc length
More generally, the arc length of a portion of the circumference, as a function of the angle subtended (or x-coordinates of any two points on the upper half of the ellipse), is given by an incomplete elliptic integral. The upper half of an ellipse is parameterized by
Then the arc length from to is:
This is equivalent to
where is the incomplete elliptic integral of the second kind with parameter
Some lower and upper bounds on the circumference of the canonical ellipse with are[20]
Here the upper bound is the circumference of a circumscribed concentric circle passing through the endpoints of the ellipse's major axis, and the lower bound is the perimeter of an inscribed rhombus with vertices at the endpoints of the major and the minor axes.
Curvature
The curvature is given by radius of curvature at point :
Radius of curvature at the two vertices and the centers of curvature:
Radius of curvature at the two co-vertices and the centers of curvature:
In triangle geometry
Ellipses appear in triangle geometry as
- Steiner ellipse: ellipse through the vertices of the triangle with center at the centroid,
- inellipses: ellipses which touch the sides of a triangle. Special cases are the Steiner inellipse and the Mandart inellipse.
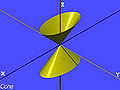
As plane sections of quadrics
Ellipses appear as plane sections of the following quadrics:
- Ellipsoid
- Elliptic cone
- Elliptic cylinder
- Hyperboloid of one sheet
- Hyperboloid of two sheets
Applications
Physics
Elliptical reflectors and acoustics
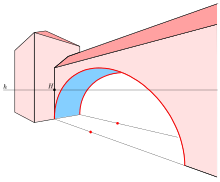
If the water's surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus. This is a consequence of the total travel length being the same along any wall-bouncing path between the two foci.
Similarly, if a light source is placed at one focus of an elliptic mirror, all light rays on the plane of the ellipse are reflected to the second focus. Since no other smooth curve has such a property, it can be used as an alternative definition of an ellipse. (In the special case of a circle with a source at its center all light would be reflected back to the center.) If the ellipse is rotated along its major axis to produce an ellipsoidal mirror (specifically, a prolate spheroid), this property holds for all rays out of the source. Alternatively, a cylindrical mirror with elliptical cross-section can be used to focus light from a linear fluorescent lamp along a line of the paper; such mirrors are used in some document scanners.
Sound waves are reflected in a similar way, so in a large elliptical room a person standing at one focus can hear a person standing at the other focus remarkably well. The effect is even more evident under a vaulted roof shaped as a section of a prolate spheroid. Such a room is called a whisper chamber. The same effect can be demonstrated with two reflectors shaped like the end caps of such a spheroid, placed facing each other at the proper distance. Examples are the National Statuary Hall at the United States Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters); the Mormon Tabernacle at Temple Square in Salt Lake City, Utah; at an exhibit on sound at the Museum of Science and Industry in Chicago; in front of the University of Illinois at Urbana–Champaign Foellinger Auditorium; and also at a side chamber of the Palace of Charles V, in the Alhambra.
Planetary orbits
In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.
More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. The other focus of either ellipse has no known physical significance. The orbit of either body in the reference frame of the other is also an ellipse, with the other body at the same focus.
Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance. Thus, in principle, the motion of two oppositely charged particles in empty space would also be an ellipse. (However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)
For elliptical orbits, useful relations involving the eccentricity are:
where
- is the radius at apoapsis (the farthest distance)
- is the radius at periapsis (the closest distance)
- is the length of the semi-major axis
Also, in terms of and , the semi-major axis is their arithmetic mean, the semi-minor axis is their geometric mean, and the semi-latus rectum is their harmonic mean. In other words,
- .
Harmonic oscillators
The general solution for a harmonic oscillator in two or more dimensions is also an ellipse. Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor. Unlike Keplerian orbits, however, these "harmonic orbits" have the center of attraction at the geometric center of the ellipse, and have fairly simple equations of motion.
Phase visualization
In electronics, the relative phase of two sinusoidal signals can be compared by feeding them to the vertical and horizontal inputs of an oscilloscope. If the Lissajous figure display is an ellipse, rather than a straight line, the two signals are out of phase.
Elliptical gears
Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.
Elliptical bicycle gears make it easier for the chain to slide off the cog when changing gears.[21]
An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine. The bobbin would need to wind faster when the thread is near the apex than when it is near the base.[22]
Optics
- In a material that is optically anisotropic (birefringent), the refractive index depends on the direction of the light. The dependency can be described by an index ellipsoid. (If the material is optically isotropic, this ellipsoid is a sphere.)
- In lamp-pumped solid-state lasers, elliptical cylinder-shaped reflectors have been used to direct light from the pump lamp (coaxial with one ellipse focal axis) to the active medium rod (coaxial with the second focal axis).[23]
- In laser-plasma produced EUV light sources used in microchip lithography, EUV light is generated by plasma positioned in the primary focus of an ellipsoid mirror and is collected in the secondary focus at the input of the lithography machine.[24]
Statistics and finance
In statistics, a bivariate random vector is jointly elliptically distributed if its iso-density contours—loci of equal values of the density function—are ellipses. The concept extends to an arbitrary number of elements of the random vector, in which case in general the iso-density contours are ellipsoids. A special case is the multivariate normal distribution. The elliptical distributions are important in finance because if rates of return on assets are jointly elliptically distributed then all portfolios can be characterized completely by their mean and variance—that is, any two portfolios with identical mean and variance of portfolio return have identical distributions of portfolio return.[25][26]
Computer graphics
Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows. Jack Bresenham at IBM is most famous for the invention of 2D drawing primitives, including line and circle drawing, using only fast integer operations such as addition and branch on carry bit. M. L. V. Pitteway extended Bresenham's algorithm for lines to conics in 1967.[27] Another efficient generalization to draw ellipses was invented in 1984 by Jerry Van Aken.[28]
In 1970 Danny Cohen presented at the "Computer Graphics 1970" conference in England a linear algorithm for drawing ellipses and circles. In 1971, L. B. Smith published similar algorithms for all conic sections and proved them to have good properties.[29] These algorithms need only a few multiplications and additions to calculate each vector.
It is beneficial to use a parametric formulation in computer graphics because the density of points is greatest where there is the most curvature. Thus, the change in slope between each successive point is small, reducing the apparent "jaggedness" of the approximation.
- Drawing with Bézier paths
Composite Bézier curves may also be used to draw an ellipse to sufficient accuracy, since any ellipse may be construed as an affine transformation of a circle. The spline methods used to draw a circle may be used to draw an ellipse, since the constituent Bézier curves behave appropriately under such transformations.
Optimization theory
It is sometimes useful to find the minimum bounding ellipse on a set of points. The ellipsoid method is quite useful for solving this problem.
See also
- Cartesian oval, a generalization of the ellipse
- Circumconic and inconic
- Distance of closest approach of ellipses
- Ellipse fitting
- Elliptic coordinates, an orthogonal coordinate system based on families of ellipses and hyperbolae
- Elliptic partial differential equation
- Elliptical distribution, in statistics
- Elliptical dome
- Geodesics on an ellipsoid
- Great ellipse
- Kepler's laws of planetary motion
- n-ellipse, a generalization of the ellipse for n foci
- Oval
- Spheroid, the ellipsoid obtained by rotating an ellipse about its major or minor axis
- Stadium (geometry), a two-dimensional geometric shape constructed of a rectangle with semicircles at a pair of opposite sides
- Steiner circumellipse, the unique ellipse circumscribing a triangle and sharing its centroid
- Superellipse, a generalization of an ellipse that can look more rectangular or more "pointy"
- True, eccentric, and mean anomaly
Notes
- ^ Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012), New Horizons in Geometry, The Dolciani Mathematical Expositions #47, The Mathematical Association of America, p. 251, ISBN 978-0-88385-354-2
- ^ The German term for this circle is Leitkreis which can be translated as "Director circle", but that term has a different meaning in the English literature (see Director circle).
- ^ "Ellipse - from Wolfram MathWorld". Mathworld.wolfram.com. 2020-09-10. Retrieved 2020-09-10.
- ^ Protter & Morrey (1970, pp. 304, APP-28)
- ^ Larson, Ron; Hostetler, Robert P.; Falvo, David C. (2006). "Chapter 10". Precalculus with Limits. Cengage Learning. p. 767. ISBN 978-0-618-66089-6.
- ^ Young, Cynthia Y. (2010). "Chapter 9". Precalculus. John Wiley and Sons. p. 831. ISBN 978-0-471-75684-2.
- ^ a b Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie, GÖTTINGEN, VANDENHOECK & RUPRECHT, 1967, p. 26
- ^ Bronstein&Semendjajew: Taschenbuch der Mathematik, Verlag Harri Deutsch, 1979, ISBN 3871444928, p. 274.
- ^ Encyclopedia of Mathematics, Springer, URL: http://encyclopediaofmath.org/index.php?title=Apollonius_theorem&oldid=17516 .
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, S. 26.
- ^ J. van Mannen: Seventeenth century instruments for drawing conic sections. In: The Mathematical Gazette. Vol. 76, 1992, p. 222–230.
- ^ E. Hartmann: Lecture Note 'Planar Circle Geometries', an Introduction to Möbius-, Laguerre- and Minkowski Planes, p. 55
- ^ W. Benz, Vorlesungen über Geomerie der Algebren, Springer (1973)
- ^ Archimedes. (1897). The works of Archimedes. Heath, Thomas Little, Sir, 1861-1940. Mineola, N.Y.: Dover Publications. p. 115. ISBN 0-486-42084-1. OCLC 48876646.
- ^ Carlson, B. C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- ^ Ivory, J. (1798). "A new series for the rectification of the ellipsis". Transactions of the Royal Society of Edinburgh. 4 (2): 177–190. doi:10.1017/s0080456800030817.
- ^ Bessel, F. W. (2010). "The calculation of longitude and latitude from geodesic measurements (1825)". Astron. Nachr. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN....331..852K. doi:10.1002/asna.201011352. S2CID 118760590. Englisch translation of Bessel, F. W. (1825). "Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen". Astron. Nachr. 4 (16): 241–254. arXiv:0908.1823. Bibcode:1825AN......4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
- ^ Ramanujan, Srinivasa (1914). "Modular Equations and Approximations to π". Quart. J. Pure App. Math. 45: 350–372. ISBN 9780821820766.
- ^ Jameson, G.J.O. (2014). "Inequalities for the perimeter of an ellipse". Mathematical Gazette. 98 (542): 227–234. doi:10.1017/S002555720000125X. S2CID 125063457.
- ^ David Drew. "Elliptical Gears". [1]
- ^ Grant, George B. (1906). A treatise on gear wheels. Philadelphia Gear Works. p. 72.
- ^ Encyclopedia of Laser Physics and Technology - lamp-pumped lasers, arc lamps, flash lamps, high-power, Nd:YAG laser
- ^ "Archived copy". Archived from the original on 2013-05-17. Retrieved 2013-06-20.
{{cite web}}: CS1 maint: archived copy as title (link) - ^ Chamberlain, G. (February 1983). "A characterization of the distributions that imply mean—Variance utility functions". Journal of Economic Theory. 29 (1): 185–201. doi:10.1016/0022-0531(83)90129-1.
- ^ Owen, J.; Rabinovitch, R. (June 1983). "On the class of elliptical distributions and their applications to the theory of portfolio choice". Journal of Finance. 38 (3): 745–752. doi:10.1111/j.1540-6261.1983.tb02499.x. JSTOR 2328079.
- ^ Pitteway, M.L.V. (1967). "Algorithm for drawing ellipses or hyperbolae with a digital plotter". The Computer Journal. 10 (3): 282–9. doi:10.1093/comjnl/10.3.282.
- ^ Van Aken, J.R. (September 1984). "An Efficient Ellipse-Drawing Algorithm". IEEE Computer Graphics and Applications. 4 (9): 24–35. doi:10.1109/MCG.1984.275994. S2CID 18995215.
- ^ Smith, L.B. (1971). "Drawing ellipses, hyperbolae or parabolae with a fixed number of points". The Computer Journal. 14 (1): 81–86. doi:10.1093/comjnl/14.1.81.
References
- Besant, W.H. (1907). "Chapter III. The Ellipse". Conic Sections. London: George Bell and Sons. p. 50.
- Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). New York: Wiley. pp. 115–9.
- Meserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry, Dover Publications, ISBN 978-0-486-63415-9
- Miller, Charles D.; Lial, Margaret L.; Schneider, David I. (1990). Fundamentals of College Algebra (3rd ed.). Scott Foresman/Little. p. 381. ISBN 978-0-673-38638-0.
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
External links
 Quotations related to Ellipse at Wikiquote
Quotations related to Ellipse at Wikiquote Media related to Ellipses at Wikimedia Commons
Media related to Ellipses at Wikimedia Commons- ellipse at PlanetMath.
- Weisstein, Eric W. "Ellipse". MathWorld.
- Weisstein, Eric W. "Ellipse as special case of hypotrochoid". MathWorld.
- Apollonius' Derivation of the Ellipse at Convergence
- The Shape and History of The Ellipse in Washington, D.C. by Clark Kimberling
- Ellipse circumference calculator
- Collection of animated ellipse demonstrations
- Ivanov, A.B. (2001) [1994], "Ellipse", Encyclopedia of Mathematics, EMS Press
- Trammel according Frans van Schooten






 원점을 중심으로 한 표준 타원의 방정식은 다음과 같습니다.
원점을 중심으로 한 표준 타원의 방정식은 다음과 같습니다.


 .표준 파라미터 방정식은 다음과 같습니다.
.표준 파라미터 방정식은 다음과 같습니다.

 거리
거리 
 2
2 타원의 중심이라고 합니다.Foci를 통과하는 선을 장축이라고 하며, 중심을 통과하는 선에 수직인 선을 단축이라고 합니다.장축은
타원의 중심이라고 합니다.Foci를 통과하는 선을 장축이라고 하며, 중심을 통과하는 선에 수직인 선을 단축이라고 합니다.장축은 


 몫은 편심률입니다.
몫은 편심률입니다.  원을 생성하며 특수한 유형의 타원에 포함된다.
원을 생성하며 특수한 유형의 타원에 포함된다.  다른 방식으로 볼 수 있습니다(그림 참조).
다른 방식으로 볼 수 있습니다(그림 참조). 






 경우
경우 (x
(x 










 > 0
> 0









 다음과 같은 좌표가 있습니다.
다음과 같은 좌표가 있습니다.











 퇴화되지 않은 경우
퇴화되지 않은 경우 





![{\displaystyle {\begin{aligned}a,b&={\frac {-{\sqrt {2{\Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{\Big )}\left((A+C)\pm {\sqrt {(A-C)^{2}+B^{2}}}\right)}}}{B^{2}-4AC}}\\x_{\circ }&={\frac {2CD-BE}{B^{2}-4AC}}\\[3pt]y_{\circ }&={\frac {2AE-BD}{B^{2}-4AC}}\\[3pt]\theta &={\begin{cases}\arctan \left({\frac {1}{B}}\left(C-A-{\sqrt {(A-C)^{2}+B^{2}}}\right)\right)&{\text{for }}B\neq 0\\0&{\text{for }}B=0,\ A<C\\90^{\circ }&{\text{for }}B=0,\ A>C\\\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)






![{\displaystyle {\begin{aligned}x(u)&=a{\frac {1-u^{2}}{1+u^{2}}}\\[10mu]y(u)&=b{\frac {2u}{1+u^{2}}}\end{aligned}}\;,\quad -\infty <u<\infty \;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c86f5ffc504dac624df3b6ce483c47521615fd18)

![{\displaystyle u\in [0,\,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)



![{\displaystyle [u:v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/297de5a93c52f13ef84add1d79d693fcda686176)
![{\displaystyle [u:v]\mapsto \left(a{\frac {v^{2}-u^{2}}{v^{2}+u^{2}}},b{\frac {2uv}{v^{2}+u^{2}}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1c21205522d70966ce62b8e324b19ec4c90f41)
![{\textstyle [1:0]\mapsto (-a,\,0).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da12e69b8138a30dcb6cfbeeb95bd63b890f2db)
 이용한 파라메트릭 표현은 표준
이용한 파라메트릭 표현은 표준 




 위쪽,
위쪽,  타원의 아래쪽입니다.수직 접선이 있는
타원의 아래쪽입니다.수직 접선이 있는
 접선의 방정식은
접선의 방정식은 
 (는) 대응하는
(는) 대응하는 




 (는) 임의 벡터입니다.
(는) 임의 벡터입니다.



 일반적으로 수직이 아닌 두
일반적으로 수직이 아닌 두 














 파라메트릭 표현을
파라메트릭 표현을 









































































































































































































![{\displaystyle x\in [-a,a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)


















![{\displaystyle {\begin{aligned}C&=2\pi a\left[{1-\left({\frac {1}{2}}\right)^{2}e^{2}-\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}{\frac {e^{4}}{3}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}{\frac {e^{6}}{5}}-\cdots }\right]\\&=2\pi a\left[1-\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}}\right]\\&=-2\pi a\sum _{n=0}^{\infty }\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}{\frac {e^{2n}}{2n-1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)




![{\displaystyle {\begin{aligned}C&=\pi (a+b)\sum _{n=0}^{\infty }\left({\frac {(2n-3)!!}{2^{n}n!}}\right)^{2}h^{n}\\&=\pi (a+b)\left[1+{\frac {h}{4}}+\sum _{n=2}^{\infty }\left({\frac {(2n-3)!!}{2^{n}n!}}\right)^{2}h^{n}\right]\\&=\pi (a+b)\left[1+\sum _{n=1}^{\infty }\left({\frac {(2n-1)!!}{2^{n}n!}}\right)^{2}{\frac {h^{n}}{(2n-1)^{2}}}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{\displaystyle C\approx \pi {\biggl [}3(a+b)-{\sqrt {(3a+b)(a+3b)}}{\biggr ]}=\pi {\biggl [}3(a+b)-{\sqrt {10ab+3\left(a^{2}+b^{2}\right)}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)









![{\displaystyle s=b\left[E\left(z\;{\Biggl |}\;1-{\frac {a^{2}}{b^{2}}}\right)\right]_{\arccos {\frac {x_{2}}{a}}}^{\arccos {\frac {x_{1}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebc2de5598b87bb3ec27bc053759d3d10cb99b4d)



















![{\displaystyle {\begin{aligned}a&={\frac {r_{a}+r_{p}}{2}}\\[2pt]b&={\sqrt {r_{a}r_{p}}}\\[2pt]\ell &={\frac {2}{{\frac {1}{r_{a}}}+{\frac {1}{r_{p}}}}}={\frac {2r_{a}r_{p}}{r_{a}+r_{p}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271)



