
Hese 정규 형태로 계산된 출발지 O에서 선 E까지의 거리. 빨간색은 정상 벡터, 녹색은 선, 파란색은 점 O. 오토 헤세의 이름을 딴 헤세 정상형식은 분석 기하학에서 사용되는 방정식으로, 2 }}개의 선이나 유클리드 R 의 평면이나
유클리드 R 의 평면이나 고차원의 하이퍼플레인을 설명한다.[1][2] 주로 거리 계산에 사용된다(점 평면 거리 및 점선 거리 참조).
고차원의 하이퍼플레인을 설명한다.[1][2] 주로 거리 계산에 사용된다(점 평면 거리 및 점선 거리 참조).
벡터 표기법으로 다음과 같이 쓰여 있다.

점dot 은(는) 스칼라 제품 또는 도트 제품을 나타낸다 . 벡터 → 좌표계의 원점인 O에서 평면이나 선 E에 정확히 놓여 있는 모든 점 P까지의 점
. 벡터 → 좌표계의 원점인 O에서 평면이나 선 E에 정확히 놓여 있는 모든 점 P까지의 점 . 벡터 → 는 평면이나 선 E의 단위 정상 벡터를 나타낸다
. 벡터 → 는 평면이나 선 E의 단위 정상 벡터를 나타낸다 . 거리는 원점 O에서 평면 또는 선까지의 최단 거리다
. 거리는 원점 O에서 평면 또는 선까지의 최단 거리다 .
.
정규 형식에서 파생/계산
참고: 단순성을 위해 다음 파생에서는 3D 사례를 설명한다. 단, 2D로도 적용 가능하다.
정상적인 형태로는

평면은 점 의 임의 위치 a→ 와
위치 a→ 와 함께 일반 벡터 → {\{에 의해 주어진다
함께 일반 벡터 → {\{에 의해 주어진다 → {n의 방향은 다음과 같은 불평등을 만족시키기 위해 선택된다
→ {n의 방향은 다음과 같은 불평등을 만족시키기 위해 선택된다 .
.

정상 벡터 → 을(를) n→ {\로 나누어 단위(또는 정규화된) 정상 벡터를 얻는다
나누어 단위(또는 정규화된) 정상 벡터를 얻는다

그리고 위의 방정식은 다음과 같이 다시 쓰여질 수 있다.

대체

우리는 헤세의 정상적인 형태를 얻는다.

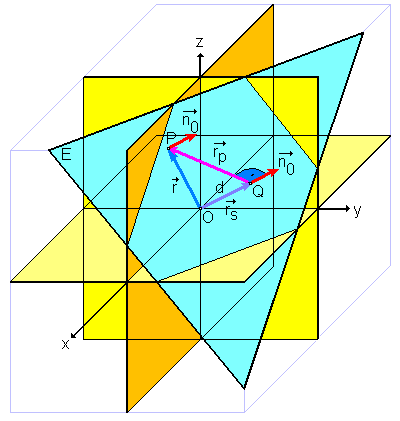
이 도표에서 d는 원점으로부터의 거리다. Because  holds for every point in the plane, it is also true at point Q (the point where the vector from the origin meets the plane E), with
holds for every point in the plane, it is also true at point Q (the point where the vector from the origin meets the plane E), with  , per the definition of the Scalar product
, per the definition of the Scalar product

→ 의 r→ 는
r→ 는 원점에서 평면까지의 최단 거리다.
원점에서 평면까지의 최단 거리다.
참조
- ^ Bôcher, Maxime (1915), Plane Analytic Geometry: With Introductory Chapters on the Differential Calculus, H. Holt, p. 44.
- ^ 존 빈스: 컴퓨터 그래픽을 위한 기하학. Springer, 2005, ISBN 9781852338343, 페이지 42, 58, 135, 273
외부 링크










 함께 일반 벡터
함께 일반 벡터 








 r
r 원점에서 평면까지의 최단 거리다.
원점에서 평면까지의 최단 거리다. 

