직교(지오메트리)

곡선의 기하학에서, 직교란 주어진 곡선의 두 접선이 직각에서 만나는 점들의 집합이다.

포물선의 정식은 그것의 다이렉트릭스(purple)이다.

타원 및 그 직교(퍼플)

직교(퍼플)가 있는 하이퍼볼라

예:

포물선의 직교성(prooftic)은 다이렉트릭스(proof: 아래 참조)이다.
는 SSLellipse .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{의 정시의.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}x2/a2+y2/b2=1은 감독 원 미국+y2)a2+b2(아래 참조),.
하이퍼볼라 $x 2 / a 2$ - $y 2 / b 2$ = $1$ , a > $b$ 는 원 x + $y 2 2$ = $a 2$ - b이다( $b 2$ b의 $경우$ 직교 접선이 없다, 아래 참조).
는 아스트 x.mw-parser-output의 정시의 .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}2⁄3+y2⁄3=는 극 방정식과 1은 quadrifolium.

r={\tfrac {1}{\\sqrt {2}}\cos(2\varphi ),\caps 0\leq \varphi <2\pi }

(아래 참조).

일반화:

이솝틱은 주어진 곡선의 두 접선이 일정한 각도에서 만나는 점의 집합이다(아래 참조).
두 평면 곡선의 이솝틱은 두 접선이 고정된 각도에서 만나는 점들의 집합이다.
화음 $PQ$ 에 대한 탈레스의 정리는 두 점 $P$ 와 $Q$ 로 퇴보되는 두 원의 직교로 간주할 수 있다.

포물선의 직교

어떤 포물선도 $y=ax^{2}$ = $y=ax^{2}$ $y=ax^{2}$ ${\$ y $=ax^{2}}$ 의 $y=ax^{2}$ 포물선으로 변형될 수 있다. The slope at a point of the parabola is $m=2ax$ . Replacing $x$ gives the parametric representation of the parabola with the tangent slope as parameter: $\ ({\tfrac {m}{2a}},{\tfrac {m^{2}}{4a}})\;.$ $\ ({\tfrac {m}{2a}},{\tfrac {m^{2}}{4a}})\;.$ 접선에는 $아직$ 알려지지 않은 n {\ $displaystyle$ n $}$ 과(와 $y=mx+n$ $)$ y $y=mx+n$ = $y=mx+n$ x $y=mx+n$ + n $y=mx+n$ 이라는 방정식이 있으며 $n$ 포물선 점의 좌표를 삽입하여 결정할 수 있다. 하나는 $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ = m $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ - $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ . ${\displaystyle$ \ $y=mx-{\tfrac{m^{2}}:{4a}\;;$ 를 얻는다. $}$

접선이 $포물선$ 을₀ 벗어나 $점 0 (x$ , y)을 포함하는 경우 방정식

y_{0}=mx_{0}-{\frac {m^{2}}:{4a}\i1\rightarrow \i1\2}-4ax_{0}\;m+4ay_{0}=0}

holds는 두 접선 통과 $(x 0,$ $y 0$ )에 해당하는 두 개의 용액 $m$ 과₁ $m$ 을₂ 가지고 있다 $.$ 감소된 2차 방정식의 자유 항은 항상 그 해결책의 산물이다. 따라서 접선이 직교적으로 ( $x 0,$ $y 0)$ 에서 만나는 경우 다음 방정식은 다음을 지탱한다.

m_{1}m_{2}=-1=4ay_{0}

마지막 방정식은 다음과 같다.

y_{0}=-{\frac {1}{4a}\;,

그게 다이렉트릭스의 방정식이야

타원형 및 하이퍼볼라의 직교

타원체

$\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ : $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ a $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ + y $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ = 1 ${\$ tfrac { $y^{2}}:{b^{2}}}}=1\}}}$ 을(를) 고려의 타원이 되게 $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ $한다$ .

(1) 인접 정점에 있는 $E$ $타원$ E $displaystyle$ $E$ $}$ 의 접선은 원하는 직교 곡선( $x^{2}+y^{2}=a^{2}+b^{2}$ $(\pm a,\pm b)$ $x^{2}+y^{2}=a^{2}+b^{2}$ 2 $x^{2}+y^{2}=a^{2}+b^{2}$ + $x^{2}+y^{2}=a^{2}+b^{2}$ $x^{2}+y^{2}=a^{2}+b^{2}$ = 2 $x^{2}+y^{2}=a^{2}+b^{2}$ + $x^{2}+y^{2}=a^{2}+b^{2}$ $x^{2}+y^{2}=a^{2}+b^{2}$ = 2 + b = $x^{2}+y^{2}=a^{2}+b^{2}$ 2 + $displaysty$ x $^{2}+y^{2$ }{\ $displaysty$ x^}{\displaystysty $})$ 에 있는 4점 $(\pm a,\pm b)$ 중 $하나$ 에서 교차한다 $(\pm a,\pm b)$ $}}=a^{2}+b^{2}}.$

(2) The tangent at a point $(u,v)$ of the ellipse $E$ has the equation ${\tfrac {u}{a^{2}}}x+{\tfrac {v}{b^{2}}}y=1$ (s. Ellipse). 이 방정식이 풀 수 있는 꼭지점이 아닌 경우: $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ = $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ - $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ $u$ $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ 2 $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ + b $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ $\ y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\;.$ ${\displaystyle$ \ y $=-{\tfrac {b^{2}u}{a^{2}v}\;x\;;;;$ $+\;{\tfrac{b^{2}}:{v}\;$ $}$

Using the abbreviations $(I)\;m=-{\tfrac {b^{2}u}{a^{2}v}},\;{\color {red}n={\tfrac {b^{2}}{v}}}\;$ and the equation ${\displaystyle \;{\color {blue}{\tfrac {u^{2}}{a^{$ ${{}}}}=1-{\tfrac{v^{2}}:{b^{2}}=1-{\tfrac{b^{2}}:{n^{2}}:}\}}$ 1은 $\;{\color {blue}{\tfrac {u^{2}}{a^{2}}}=1-{\tfrac {v^{2}}{b^{2}}}=1-{\tfrac {b^{2}}{n^{2}}}}\;$ 다음과 같은 $효과$ 를 얻는다.

m^{2}={\frac {b^{4}u^{2}}{a^{4}v^{2}}}={\frac {1}{a^{2}}}{\color {red}{\frac {b^{4}}{v^{2}}}}{\color {blue}{\frac {u^{2}}{a^{2}}}}={\frac {1}{a^{2}}}{\color {red}n^{2}}{\color {blue}(1-{\frac {b^{2}}{n^{2}}})}={\frac {n^{2}-b^{2}}{a^{2}}}\;.

따라서 $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ ( $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ ) $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ = $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ ± m $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ + b $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ ${\$ \ $(II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2$ } $}}}}$ 과 $\ (II)\;n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$ (와) 비 수직 탄젠트의 방정식은

y=m\;x\;\pm {\sqrt {m^{2}a^{2}+b^{2}}.

$u$ , $v$ $u,v$ 및 존중 $u,v$ $(II)$ ) ${\displaystyle i)$ 에 대한 관계 $($ I $(I)$ )를 해결하면 $(II)$ 타원의 파라메트릭 표현에 따라 기울기가 발생한다.

{\

}}}}\,\;{\tfrac {b^{2}}:{\pm {\sqrt{m^{2}a^{2}+b^{2

}}}}\ .\

}(

(u,v)=(-{\tfrac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\;,\;{\tfrac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}})\ .\

다른 증거는: 타원을 참조하십시오.)

접선에 점 $(x_{0},y_{0})$ $(x_{0},y_{0})$ , $(x_{0},y_{0})$ 0 $(x_{0},y_{0})$ ) ${\displaystyle(x_{0},y_{0}}})$ 이 포함되어 있으면 타원으로부터 떨어진 방정식이 있다.

y_{0}=mx_{0}\pm {\sqrt {m^{2}a^{2}+b^{2}}}}

정사각형 근을 제거하면

m^{2}-{0}y_{0}}}{0}}{0}^{0}-{0}^{2}m+{\frac {y_{0}^{0}-b^{2}}:{x_{0}-b^{0}-{0}-a^{2}}}}=0,0,}}}

두 개의 용액 $m_{1},m_{2}$ $m_{1},m_{2}$ , $m_{1},m_{2}$ 2 ${\$ 2}}개가 $있으며$ $(x_{0},y_{0})$ 이는 지나가는 두 개의 접선( $(x_{0},y_{0})$ $(x_{0},y_{0})$ , $(x_{0},y_{0})$ $(x_{0},y_{0})$ ) $(x_{0},y_{0}}}}$ 에 해당된다 $m_1,m_2$ $(x_{0},y_{0})$ 일차 이차 방정식의 상수 항은 항상 그 해결책의 산물이다. 따라서 접선이 직교적으로 $(x_{0},y_{0})$ ( $(x_{0},y_{0})$ x $(x_{0},y_{0})$ , $(x_{0},y_{0})$ y $(x_{0},y_{0})$ ) ${\displaystyle$ ( $x_{0},y_{0}}}$ 에서 만나는 경우 다음 방정식은 다음을 유지한다.

원, 타원 및 하이퍼볼라의 직교(빨간색 원)

{\displaystyle m_{1}m_{2}=-1={\frac {y_{0}^{2}-b^{2}}:{x_{0}^{0}^{2}-a^{2}}:

마지막 방정식은 다음과 같다.

x_{0}^{2}+y_{0}}^{2}=a^{2}+b^{2}\;.

(1)과 (2)에서 다음과 같은 것을 얻는다.

직교 접선의 교차점은 원 $x^{2}+y^{2}=a^{2}+b^{2}$ $x^{2}+y^{2}=a^{2}+b^{2}$ + $x^{2}+y^{2}=a^{2}+b^{2}$ 2 $x^{2}+y^{2}=a^{2}+b^{2}$ = $x^{2}+y^{2}=a^{2}+b^{2}$ + $x^{2}+y^{2}=a^{2}+b^{2}$ $x^{2}+y^{2}=a^{2}+b^{2}$ ${\$ }의 점이다. $}}=a^{2}+b^{2}}.$

하이퍼볼라

타원형 케이스는 거의 정확히 하이퍼볼라 케이스에 채택할 수 있다. b $b^{2}$ ${\$ 개를 $-b^{2}$ - b $-b^{2}$ ${\$ 개로 $b^{2}$ 교체하고 $-b^{2}$ $m$ ~ $m$ > $b / a$ 로 제한해야 한다. 따라서 다음과 같다.

직교 접선의 교차점은 원 $x^{2}+y^{2}=a^{2}-b^{2}$ 2 $x^{2}+y^{2}=a^{2}-b^{2}$ + $x^{2}+y^{2}=a^{2}-b^{2}$ 2 $x^{2}+y^{2}=a^{2}-b^{2}$ = $x^{2}+y^{2}=a^{2}-b^{2}$ - $x^{2}+y^{2}=a^{2}-b^{2}$ $x^{2}+y^{2}=a^{2}-b^{2}$ ${\$ }의 점이다. $}}=a^{2}-b^{2$ $여기$ 서 a > $b$ .

아스트로이드의 직교

아스트로이드의 직교(퍼플)

아스트로이드는 모수적 표현으로 설명할 수 있다.

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

→ (

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

)

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

=

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

(

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

,

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

)

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

,

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

<

{\vec {c}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi

{\

displaystyle {\vec}}}(t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad

0

\leq<2\pi

.

조건으로부터

{\vec}{\dot{c}(t)\cdot {\vec}(t+\dot )=0

$ċ \to(t)$ 에 직교 접선이 나타나는 매개변수 공간의 거리 $α$ 를 인식한다. 거리는 매개변수 $t$ , 즉 $α =$ ± $π / 2$ 와 무관하다는 것이 밝혀졌다. $c \to(t)$ 및 $c \to(t$ + $π / 2$ )점에 있는 (직교) 접선의 방정식은 각각 다음과 같다.

{\ligned}y&=-\tan t(x-\cos ^{3}t\right)+\sin ^{3}t,\\y&={\frace{1}{1}}}\t}왼쪽(x+\sin ^}t\right)+\cos ^{3}t.\end{정렬}}

공통점에는 다음과 같은 좌표가 있다.

#\displaystyle {\sin t-\cos t(\sin t-\cos t)\\sin t=\sin t+\cos t(\sin t+\cos t)\\cos t(\sin t+\cos t.\end{정렬}}}

이것은 동시에 정자의 파라메트릭 표현이다.

매개변수 $t$ 를 제거하면 암묵적 표현이 나타난다.

2\좌(x^{2}+y^{2}\우)^{3}-\좌(x^{2}-y^{2}\우)^{2}=0.

새로운 파라미터 $introducing$ = $t$ - 5 $5 / 4$ 를 도입한다.

{\barphi}x&={\tfrac {1}{\sqrt{2}}\cos(2\varphi )\cos \varphi ,\y&={\tfrac {1}{\sqrt{2}}}\cos(2\varphi )\sinvarphi.end{}}}}}

(검증은 각도 합과 차이 식별을 사용한다.) 그래서 우리는 극의 표현을 얻는다.

r={\tfrac {1}{\\sqrt {2}}\cos(2\varphi ),\caps 0\leq \varphi <2\pi }

정격의 따라서 다음과 같다.

아스트로이드의 정식은 4중골이다.

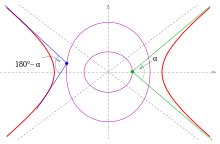
포물선, 타원, 하이퍼볼라의 이솝틱

80° 및 100° 각도에 대한 포물선의 이솝틱스(퍼플)

80° 및 100° 각도에 대한 타원의 이솝틱스(퍼플)

80° 및 100° 각도에 대한 하이퍼볼라의 이솝틱스(퍼플)

각도 $α$ ≠ $90°$ 에 대한 동위원소 아래에 열거되어 있다. 그것들은 α-이솝틱스라고 불린다. 자세한 내용은 아래를 참조하십시오.

이솝틱스 방정식

포물선:

등식 $y$ = $도끼$ 가² 있는 포물선의 α 이등분자는 하이퍼볼라의 가지다.

x^{2}-\tan ^{2}\{2}\proc{1}{4a}\right)^{2}-{\frac {a}}=0.

하이퍼볼라의 가지들은 두 각 $α$ 와 $180°$ - $α$ 에 대해 이솝소틱을 제공한다(그림 참조).

타원:

등식 $x 2 / a 2$ + $y 2 / b 2$ = $1$ 을 갖는 타원의 α-이소포틱스는 도-4 곡선의 두 부분이다.

\left(x^{2}+y^{2}-a^{2}-a^{2}-b^{2}\right)^{2}\tan^{2}\ft=4\ft(a^{2}y^{2}y^{2}+b^{2}){2}x^{2}-a^{2}b^{2}\오른쪽)

(그림 참조).

하이퍼볼라:

$x 2 / a 2$ - $y 2 / b 2$ = $1$ 등식을 갖는 하이퍼볼라의 α-이소방틱스는 도-4 곡선의 두 부분이다.

\left(x^{2}+y^{2}-a^{2}+b^{2}}\right)^{2}\tan^{2}\cHB =4\left(a^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}\right)

교정쇄

포물선:

$포물선$ y = $도끼$ 는² $접선$ m = $2ax$ :

{\vec}(m)=\왼쪽({\frac {m}{2a},{\frac {m^{2}}:{4a}\오른쪽),\quad m\in \mathb {R}.

경사 $m$ 의 접선에는 방정식이 있다.

y=mx-{\frac {m^{2}}{4a}}.

점 $(x 0,$ $y 0)$ 은 다음과 같은 경우에만 접선에 위치한다.

y_{0}=mx_{0}-{\frac {m^{2}}{4a}}.

이는 ( $x 0,$ y $)$ 를₀ 포함하는 두 접선의 경사 m, $m$ 이₁₂ 2차 방정식을 충족함을 의미한다.

m^{2}-4ax_{0}m+4ay_{0}=0.

접선이 각도 $α$ 또는 $180°$ 에서 만나는 경우 - $α$ , 등식

\tan ^{2}\cHB =\lefted\frac {m_{1}-m_{2}}:{1+m_{1}m_{2}}\오른쪽)^{2

반드시 이루어져야 한다. $m$ 에 대한 2차 방정식을 풀고, 마지막 $방정식$ 에₁ m, $m$ 을₂ 삽입하면,

x_{0}^{2}-\tan ^{2}\reft(y_{0}+{\frac{1}{4a}\오른쪽)^{2}-{\frac {y_{0}}}=0}=0.

이것이 위의 하이퍼볼라의 방정식이다. 그것의 가지에는 두 각 $α$ 와 $180°$ - $α$ 에 대한 포물선의 두 이등분자가 있다.

타원:

타원 x/ $a 2$ + $y 2$ / $b 2 2$ = $1$ 의 경우 2차 방정식에 대한 직교 개념을 채택할 수 있다.

m^{2}-{0}y_{0}}}{0}}{0}^{0}-{0}^{2}m+{\frac {y_{0}^{0}-b^{2}}:{x_{0}-a^{2}-2}}:0}=0.

이제 포물선의 경우와 마찬가지로 2차 방정식을 풀고 두 용액 $m 1$ , $m$ 을₂ 방정식에 삽입해야 한다.

\tan ^{2}\cHB =\lefted\frac {m_{1}-m_{2}}:{1+m_{1}m_{2}}\오른쪽)^{2}

재배열은 이솝소틱이 도-4 곡선의 일부라는 것을 보여준다.

\left(x_{0}^{2}+y_{0}}^{2}-a^{2}-b^{2}}\right)^{2}\tan^{2}\tan^{2}\ft=4\reft(a^{2}y_{0}^{2}+b^{2}}x_{0}^{2}-a^{2}b^{2}\오른쪽).

하이퍼볼라:

하이퍼볼라의 경우 용액은 $타원형 2$ 케이스에서 $b$ 를² -b로 대체하여 채택할 수 있다(정형체의 경우, 위 참조).

이등분석을 시각화하려면 암시적 곡선을 참조하십시오.

외부 링크

메모들

참조

Lawrence, J. Dennis (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5.
Odehnal, Boris (2010). "Equioptic Curves of Conic Sections" (PDF). Journal for Geometry and Graphics. 14 (1): 29–43.
Schaal, Hermann (1977). "Lineare Algebra und Analytische Geometrie". III. Vieweg: 220. ISBN 3-528-03058-5. Cite 저널은 필요로 한다. journal= (도움말)
Steiner, Jacob (1867). Vorlesungen über synthetische Geometrie. Leipzig: B. G. Teubner. Part 2, p. 186.
Ternullo, Maurizio (2009). "Two new sets of ellipse related concyclic points". Journal of Geometry. 94: 159–173.

hide v t 평면 곡선의 차동 변환
단항작업	에볼루트 비자발적 이중 곡선 역곡선 평행 곡선 이솝틱
점으로 정의된 단항 연산	페달 & 대칭 곡선 음극 페달 곡선 추격곡선 가우스틱
두 점으로 정의된 단항 연산	스트롭호이드
점으로 정의된 이진 연산	룰렛 시스소이드
곡선 계열의 작업	봉투

Search