토너먼트 솔루션
Tournament solution| 정치 시리즈의 일부 |
| 선거 제도 |
|---|
 |
| |
토너먼트 솔루션은 방향 완전 그래프를 정점의 비어 있지 않은 부분 집합에 매핑하는 함수입니다.그것은 비공식적으로 토너먼트에서 서로 경쟁하는 모든 대안들 중에서 "최고의" 대안을 찾는 방법으로 생각될 수 있다.토너먼트 솔루션은 사회적 선택 [1][2][3][4]이론에서 비롯되었지만 스포츠 경기, 게임 이론,[5] 다중 기준 결정 분석, 생물학,[6][7] 웹 페이지 순위 [8]및 결투 강도 [9]문제에서도 고려되었습니다.
사회적 선택 이론의 맥락에서 토너먼트 솔루션은 피시번의 C1 사회적 선택 [10]기능과 밀접하게 관련되어 있기 때문에 모든 후보 중에서 누가 가장 좋은 후보인지를 보여주는 것을 추구합니다.
정의.
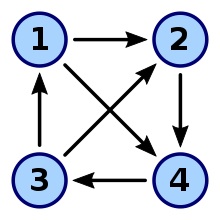
토너먼트(그래프) T는 튜플입니다.서 A 는 정점 세트(대체)이며,{는 정점 위의 연결 및 비대칭 이진 관계입니다.사회적 선택 이론에서, 이항 관계는 전형적으로 대안들 사이의 쌍대 다수결 비교를 나타낸다.
토너먼트 솔루션은 각 ( A, ){ T = ( , \ )} 를 A{ \ A} (선택[2] 세트라고 함)의 비어있지 않은 f (에 매핑하는 함수f { f( 입니다.
- : \ h :A는 두 T ( , ) { T= ( A , \ succ )} T~ ( , ~) { T } = ( B , { \ { T}) , \ widetildeen ) )。
예
토너먼트 솔루션의 일반적인 예는 다음과 같습니다.[1][2]
레퍼런스
- ^ a b Laslier, J.-F. (1997). Tournament Solutions and Majority Voting. Springer Verlag.
- ^ a b c Felix Brandt; Markus Brill; Paul Harrenstein (28 April 2016). "Chapter 3: Tournament Solutions" (PDF). In Felix Brandt; Vincent Conitzer; Ulle Endriss; Jérôme Lang; Ariel D. Procaccia (eds.). Handbook of Computational Social Choice. Cambridge University Press. ISBN 978-1-316-48975-8.
- ^ Brandt, F. (2009). Tournament Solutions - Extensions of Maximality and Their Applications to Decision-Making. Habilitation Thesis, Faculty for Mathematics, Computer Science, and Statistics, University of Munich.
- ^ Scott Moser. "Chapter 6: Majority rule and tournament solutions". In J. C. Heckelman; N. R. Miller (eds.). Handbook of Social Choice and Voting. Edgar Elgar.
- ^ Fisher, D. C.; Ryan, J. (1995). "Tournament games and positive tournaments". Journal of Graph Theory. 19 (2): 217–236. doi:10.1002/jgt.3190190208.
- ^ Allesina, S.; Levine, J. M. (2011). "A competitive network theory of species diversity". Proceedings of the National Academy of Sciences. 108 (14): 5638–5642. doi:10.1073/pnas.1014428108. PMC 3078357. PMID 21415368.
- ^ Landau, H. G. (1951). "On dominance relations and the structure of animal societies: I. Effect of inherent characteristics". Bulletin of Mathematical Biophysics. 13 (1): 1–19. doi:10.1007/bf02478336.
- ^ Felix Brandt; Felix Fischer (2007). "PageRank as a Weak Tournament Solution" (PDF). Lecture Notes in Computer Science (LNCS). 3rd International Workshop on Internet and Network Economics (WINE). Vol. 4858. San Diego, USA: Springer. pp. 300–305.
- ^ Siddartha Ramamohan; Arun Rajkumar; Shivani Agarwal (2016). Dueling Bandits: Beyond Condorcet Winners to General Tournament Solutions (PDF). 29th Conference on Neural Information Processing Systems (NIPS 2016). Barcelona, Spain.
- ^ Fishburn, P. C. (1977). "Condorcet Social Choice Functions". SIAM Journal on Applied Mathematics. 33 (3): 469–489. doi:10.1137/0133030.


 튜플
튜플
 정점 세트(대체)이며,
정점 세트(대체)이며, 정점 위의
정점 위의 
 매핑하는
매핑하는 
 두
두 


