할바흐 어레이

Halbach 어레이의 플럭스 다이어그램

각 피스의 자기장의 방향을 나타내는 할바흐 어레이.이 배열은 아래에 강력한 필드를 제공하지만 위의 필드는 취소됩니다.

선형 Halbach 어레이의 강변과 약변 방향(강변 위)

선형 Halbach 어레이의 강변과 약변 방향(약변 위)

Halbach 어레이는 어레이의 한쪽에서는 자기장을 증가시키고 다른 ^[1]^[2]한쪽에서는 자기장을 거의 0으로 소거하는 영구 자석의 특별한 배열입니다.이는 공간적으로 회전하는 자화 패턴을 통해 달성됩니다.

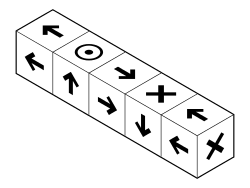
영구 자석의 회전 패턴(전면, 왼쪽, 위쪽, 오른쪽, 아래쪽)은 무기한 지속할 수 있으며 동일한 효과를 발휘합니다.이 배열의 효과는 비슷한 극이 서로 맞닿아 있는 많은 말굽 자석과 거의 유사합니다.

이 원리는 제임스 M에 의해 처음 발명되었다.1970년 Magnepan의 Wenny는 단측 스트라이프 모양의 ^[3]코일에 의해 유도되는 연속 회전 자화의 이상적인 경우에 사용되었습니다.

그 효과는 또한 John C에 의해 발견되었다. 1973년 Mallinson과 이러한 "단측 플럭스" 구조는 처음에 그가 "호기성"이라고 설명했지만, 그는 이 발견으로 인해 자기 테이프 ^[4]기술의 상당한 개선 가능성을 인식했다.

물리학자 클라우스 할바흐는 1980년대 로렌스 버클리 국립연구소에 있을 때 입자 가속기 ^[5]빔에 초점을 맞추기 위해 독립적으로 할바흐 어레이를 발명했다.

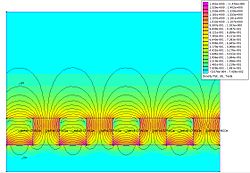
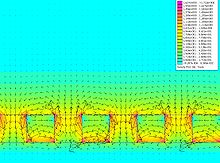
선형 어레이

자화

자성분 소거로 인해 단측 플럭스 발생

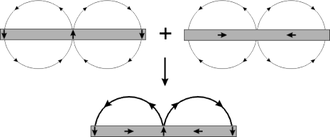
이러한 자속 분포는 단순한 막대 자석이나 솔레노이드에 익숙한 사람들에게는 다소 직관에 반하는 것처럼 보이지만, 이러한 자속 분포의 이유는 Mallinson의 원래 다이어그램을 사용하여 직관적으로 시각화할 수 있다(Mallinson 기사의 다이어그램과 달리 음의 y 성분을 사용한다는 점에 유의하십시오).이 다이어그램은 Y 방향(왼쪽 위)과 X 방향(오른쪽 위)으로 번갈아 자화된 강자성 재료 스트립의 필드를 보여 줍니다.평면 위의 필드는 두 구조 모두에서 같은 방향이지만 평면 아래의 필드는 반대 방향입니다.이 두 구조를 겹치는 효과는 그림에 나와 있습니다.

중요한 점은 플럭스가 평면 아래에서 상쇄되고 평면 위로 강화된다는 것입니다. $실제로$ 자화 성분이 서로 위상이 맞지 $\pi /2$ $\pi /2$ 자화 $패턴$ 은 단측 플럭스를 발생시킵니다 $.$ 일부 함수의 모든 성분의 위상을 $\pi /2$ / $(\displaystyle \pi / 2$ )만큼 $\pi /2$ 이동하는 수학적 변환을 힐버트 변환이라고 합니다.따라서 자화 벡터의 성분은 힐버트 변환 쌍이 될 수 있습니다(그 중 $\sin(x)\cos(y)$ 단순한 것은 sin $\sin(x)\cos(y)$ ( $\sin(x)\cos(y)$ x ) cos $\sin(x)\cos(y)$ ( $\sin(x)\cos(y)$ y $\sin(x)\cos(y)$ ) \ $displaystyle$ \ $sin(x)$ \cosy $\sin(x)\cos(y)$ )입니다).를 참조해 주세요).

입방체 자석의 무한 할바흐 배열 주위의 자기장.사용되는 개별 자석으로 인해 필드가 완전히 취소되지 않습니다.

이상적이고 지속적으로 변화하는 무한 배열의 취소되지 않는 쪽의 필드는 다음과 같습니다^[6].

F(x,y)=F_{0}e^{ikx}e^{-ky}

어디에

F(x,y)

(

F(x,y)

,

F(x,y)

) {

displaystyle

F (

x

,

y

) the

F(x,y)

、

F_{x}+iF_{y}

+

F_{x}+iF_{y}

F_{x}+iF_{y}

( \

displaystyle

F _ {

x

} +

iF _

{ y

F_{x}+iF_{y}

)

F_{x}+iF_{y}

f f 。

F_{0}

0

(\

은

F_{0}

어레이 표면의 필드 크기입니다.

k

{

display style

k

}는

k

파수(공간 주파수)

2\pi /\lambda

/

（

\

display

2 \

pi

/ \

displayda

입니다.

적용들

단측 플럭스 분포의 장점은 두 가지입니다.

이 필드는 플럭스가 구속된 쪽의 두 배입니다(이상적인 경우).
반대편에는 (이상적인 경우) 유영장이 생성되지 않습니다.이는 일반적으로 자기 구조 설계의 문제인 필드 구속에 도움이 됩니다.

비록 일방적인 자속 분포 다소 추상적인 것처럼 보일지라도, 그들은 애플리케이션 냉장고 자석은 브러실 리스 DC모터, wiggler 자석 입자 가속기와 free-elect에 사용된 첨단 응용 프로그램에 목소리 coils,[7]자기 약 targeting[8] 같은 산업적 응용까지 이르는 놀랄 만한 수의고 있다.ron 라sers.

이 장치는 또한 인덕트랙 자기부상열차와^[9] 인덕트랙 로켓 ^[10]발사 시스템의 핵심 부품으로, Halbach 어레이는 열차가 들어올릴 수 있는 속도로 가속된 후 선로를 형성하는 와이어의 루프를 격퇴합니다.

냉장고 자석의 플럭스 분포

단측 플럭스 자석의 가장 간단한 예는 냉장고 자석이다.이것들은 보통 플라스틱이나 고무와 같은 바인더에 가루로 된 페라이트들로 구성되어 있습니다.압출된 자석은 회전장에 노출되어 자성 화합물 내의 페라이트 입자에 자화를 가함으로써 일방적인 플럭스 분포를 초래합니다.이 분포는 예를 들어 자성 화합물의 균일한 자화에 의한 유지력에 비해 투과성 표면에 놓였을 때 자석의 유지력을 증가시킵니다.

자유 전자 레이저의 개략도

이 디자인을 스케일업하고 톱시트를 추가하면 싱크로트론 및 자유전자 레이저에 사용되는 위글러 자석이 생성됩니다.위글러 자석은 전자빔을 자기장에 수직으로 흔들거나 진동시킵니다.전자는 가속을 거치면서 비행 방향으로 전자파 에너지를 방출하고, 이미 방출된 빛과 상호작용할 때, 그 선을 따라 광자가 위상별로 방출되어 "레이저 같은" 단색 간섭성 빔을 생성한다.

위에 표시된 디자인은 보통 Halbach 위글러로 알려져 있습니다.자화 시트의 자화 벡터는 서로 반대 방향으로 회전합니다.상부 시트의 자화 벡터는 시계 방향으로 회전하고, 하부 시트의 자화 벡터는 시계 반대 방향으로 회전합니다.이 설계는 시트에서 자기장의 x 성분이 취소되고 y 성분이 보강되도록 선택되며 다음과 같이 필드가 주어집니다.

apprough \cos(kxdisplaystyledisplaystyle H_{y}\about \(kx)

여기서 k는 동일한 자화 벡터를 가진 자기 블록 사이의 간격에 의해 주어진 자기 시트의 파수입니다.

리니어

의 등가 (Halbach)

축에 수직으로 자화된 일련의 자기봉은 할바흐 어레이로 배열할 수 있다.그 후 각 로드를 90° 교대로 회전시키면 그림에 도식적으로 나타나듯이 로드의 평면 한쪽에서 다른 쪽으로 이동한다.

이 배치는 로드의 회전에 따라 로드의 평면 위 또는 아래에서 필드를 효과적으로 온/오프할 수 있도록 한다.이러한 장치는 전력을 필요로 하지 않는 효율적인 기계식 자기 래치를 만듭니다.이러한 배치에 대한 자세한 연구 결과, 각 로드는 인접 로드의 강한 토크를 받기 때문에 기계적 ^[11]안정화가 필요한 것으로 나타났습니다.그러나 안정성과 각 로드를 번갈아 회전시키는 기능을 모두 제공하는 간단하고 효율적인 솔루션은 그림과 같이 각 로드에 등가 기어 배치를 제공하는 것입니다.

★★★★★★★★★★★★★★★★★」

한

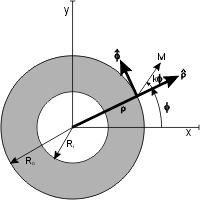
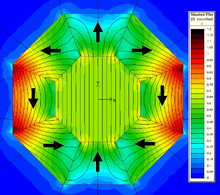
Halbach 실린더는 강자성 재료로 구성된 자화 실린더로, 외부에는 0개의 전계가 있는 상태에서 실린더 안에 완전히 갇힌 강도 높은 자기장을 생성합니다(이상적인 경우).실린더는 또한 자기장이 실린더 내부에 0인 상태에서 완전히 실린더 외부에 있도록 자화할 수 있습니다.그림에는 몇 가지 자화 분포가 나와 있습니다.

재료 이며, 강자성 재료의 자화 방향은 축에 수직인 평면이다.

M왼쪽(\- {\}+\sin \left)\left- {\fright}\ hatright) {\fright}{{{\}\what}\ hatt}\wide 모자\right) {{\wh}\wh}\wide 모자

여기서_r M은 강자성 잔류(A/m)입니다.k - 1의 양의 값은 내부 자기장을, 음의 값은 외부 자기장을 나타냅니다.

이상적으로는 이러한 구조는 자화 방향이 지속적으로 변화하는 자성 물질의 무한 길이 원통에서 생성됩니다.이 이상적인 설계에 의해 생성되는 자속은 완벽하게 균일하며 실린더의 보어 또는 실린더의 외부로 완전히 제한됩니다.물론, 무한 길이의 이상적인 경우는 실현 가능하지 않으며, 실제로 실린더의 유한한 길이는 최종 효과를 발생시켜 현장에서 ^[12]^[13]불균일성을 초래한다.또한 지속적으로 변화하는 자성을 가진 실린더를 제작하는 것이 어렵기 때문에 설계가 분할되는 경우가 많습니다.

프로그램

이러한 원통형 구조는 브러시리스 AC 모터, 자기 커플링 및 하이필드 실린더와 같은 장치에 사용됩니다. 모두 필드 합니다.

브러시리스 모터는 일반적으로 모든 플럭스가 보어의 중심(위의 k = 4, 6극 로터 등)으로 제한되는 원통형 설계를 사용하며 보어 내부에도 AC 코일이 포함되어 있습니다.이러한 셀프 실드 모터 설계는 기존 모터 설계보다 더 효율적이고 높은 토크를 생성합니다.
자기 결합 장치는 예를 들어 밀폐된 용기 또는 가압된 용기 사이에서 자기 투명 장벽(즉, 장벽은 비자성 또는 자성이지만 적용된 자기장의 영향을 받지 않음)을 통해 토크를 전달합니다.최적의 토크 커플링은 +k 및 -k 플럭스 자화 패턴이 반대인 한 쌍의 동축 중첩 실린더로 구성됩니다. 이 구성은 무한히 ^[14]긴 실린더가 토크를 생성하는 유일한 시스템이기 때문입니다.최저 에너지 상태에서는 내통 외통속은 외통 내통속과 정확하게 일치한다.이 상태에서 한 실린더를 다른 실린더에 대해 회전시키면 토크가 복원됩니다.

한 필드

Halbach Halbach

k = 2의 특수한 경우, 보어 내부의 장은 균일하며 다음과 같이 주어진다.

Htext{displaystyle H=M_{r}\ln \leftfrac {R_{\text}}}{R_{text}}}}{text}}}}}}{right}}}}{R_{right}}}}}{R}}}}}}}}}

여기서 내측 및 외측 실린더 반지름은 각각_i R 및_o R이다.H는 y방향이다.이것은 할바흐 실린더의 가장 단순한 형태이며, 외측과 내측 반지름의 비율이 e보다 크면 보어 내부의 플럭스가 실제로 실린더를 만드는 데 사용된 자성 물질의 잔류량을 초과한다는 것을 알 수 있습니다.그러나 사용된 영구 자석의 보자기력을 초과하는 자기장이 생성되지 않도록 주의해야 한다. 이는 실린더의 소자 및 ^[15]^[16]의도한 것보다 훨씬 낮은 자기장이 생성될 수 있기 때문이다.

하는 3가지 설계

이 원통형 설계는 영구 자석 배열 내의 공동 내부에서 균일한 필드를 생성하는 설계 클래스 중 하나에 불과합니다.아벨리 젠센은 아벨리 젠센이다.

(A)의 웨지 자화 방향은 Abelle이 제시한 일련의 규칙을 사용하여 계산할 수 있으며 캐비티 형상의 큰 자유도를 가능하게 한다.또 다른 설계 클래스는 Coey와 Cugat이 ^[17]^[18]제안한 자기 망글(B)로, 6로드 설계에서와 같이 균일하게 자화된 로드가 할바흐 실린더와 일치하도록 배치되어 있습니다.이 설계는 균일한 필드의 부피가 원통형 설계보다 작기 때문에 균일한 필드의 영역에 대한 접근을 크게 증가시킨다(단, 이 영역은 구성 요소 로드의 수를 증가시켜 더 크게 만들 수 있다).로드를 서로 상대적으로 회전시키면 동적으로 가변적인 필드 및 다양한 쌍극자 구성을 포함하여 많은 가능성이 발생합니다.(A)와 (B)의 설계는 k = 2 Halbach 실린더와 밀접한 관련이 있음을 알 수 있다.균일 장에 대한 다른 매우 단순한 설계에는 그림 (C)와 같이 부드러운 철 리턴 경로를 가진 분리된 자석이 포함됩니다.

최근 몇 년 동안 이러한 Halbach 쌍극자는 저장 NMR ^[19]실험을 수행하기 위해 사용되어 왔다.상용화된 (Bruker Minispec) 영구 자석의 표준 플레이트 형상(C)과 비교하여, 위에서 설명한 바와 같이 보어 직경이 크면서도 상당히 균일한 필드를 유지합니다.

인

실린더에 의해 생성된 필드를 찾는 데 사용되는 방법은 수학적으로 균일하게 자화된 ^[20]구를 조사하는 데 사용되는 방법과 매우 유사합니다.

실린더 축을 따른 배열의 대칭성 때문에 이 문제는 2차원으로 처리될 수 있습니다.plane-polar 좌표에 종사하다{\displaystyle(r,\theta)}관련 단위 벡터와이었고 넌 결코 모르네 ^{\displaystyle{\hat{\mathbf{r}}}}과θ ^{\displaystyle{\hat{\boldsymbol{\theta}}}}, &lt의 r. 실린더의 방사 범위 하게 내버려두며<>(r, θ), r({\displaystyle r_{\mathrm{나는}}<>r&.그것은, r_{\mathrm ${o}$ 그러면 $M_{0}$ $M_{0}$ 0 $({$ 인 실린더 벽면의 자화가 부드럽게 $회전$ 합니다.

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

c

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

0 (

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

r

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

+

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

^

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

^

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

^ ) {

display style

\

mathbf {

M }

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

_ { \

mathrm

{ }

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

=

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

M _

0

（

cos

\

theta

} 、 { \

hat \ mathbf

{

r

}

}

}

\mathbf {M} _{\mathrm {cyl} }=M_{0}(\cos \theta \,{\hat {\mathbf {r} }}+\sin \theta \,{\hat {\boldsymbol {\theta }}})

、

벽 밖에서 자화가 사라지는 동안, 즉 $r<r_{\mathrm {i} }$ r < $r<r_{\mathrm {i} }$ $r<r_{\mathrm {i} }$ \ $displaystyle$ r < r $_$ r _ { \ $mathrm$ { $i }$ } surround $r<r_{\mathrm {i} }$ surround $r>r_{\mathrm {o} }$ surround > $r>r_{\mathrm {o} }$ > r $r>r_{\mathrm {o} }$ \ $display$ r > r $r>r_{\mathrm {o} }$ _ { \ $mathrm$ { }} $r>r_{\mathrm {o} }$ 。

정의상 보조 자기장 $\mathbf {H}$ H $(\$ 는 $\mathbf{H}$ B $=$ $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ 0 ( $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ + M $)$ (\ $displaystyle \mathbf {B}$ $\mathbf {B}$ =\ $mu _0}$ (\ $displaystyle$ \mathbf ${H}$ + $mathb})$ 의 자속 $\mathbf {B}$ B $(\$ B})와 $\mathbf {B}$ 관련이 있다. $abla \cdot \mathbf {B} =0$ 이는 동등합니다.

\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M}

∇

\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M}

-

\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M}

⋅

M

\

displaystyle

\

cdot

\

mathbf

{ H } = - \

cdot

\

mathbf

{ M

\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M}

}

\nabla \cdot \mathbf {H} =-\nabla \cdot \mathbf {M}

(1)

문제는 정적이기 때문에 자유 전류가 없고 모든 시간 도함수가 사라지기 때문에 Amper의 법칙은 추가로 $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \phi$ × $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \phi$ $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \phi$ $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \phi$ † H $=$ $\nabla \times \mathbf {H} =0\implies \mathbf {H} =\nabla \phi$ { $displaystyle \ times$ \ $mathbf { H$ } $=$ 0 \ $displaystyle$ \ $mathbf$ { $H$ } = \ $la$ \ $phi$ ({ displaystyle \ displaystyle })를 $\phi$ 요구합니다. 여기서 = \ $\phi$ \ phyle ） $=$ \ $phi$ )이것을 H $(\$ 와 $\mathbf{H}$ M $(\$ 을 $\mathbf {H}$ 하는 이전의 방정식 1에 대입하면, 우리는 풀어야 한다는 것을 알게 된다.

\nabla ^{2}\phi =-\nabla \cdot \mathbf {M}

\nabla ^{2}\phi =-\nabla \cdot \mathbf {M}

-

\nabla ^{2}\phi =-\nabla \cdot \mathbf {M}

⋅

M

\

\nabla ^{2}\phi =-\nabla \cdot \mathbf {M}

displaystyle \

phi =

- \

displayla

\

cdot

\

mathbf

{ M

\nabla ^{2}\phi =-\nabla \cdot \mathbf {M}

,

(2)

포아송 방정식의 형태를 띠고 있습니다.

이제 실린더-공기 $r=r_{\mathrm {i} }$ r $r=r_{\mathrm {i} }$ $r=r_{\mathrm {i} }$ {\ $displaystyle$ r $=r_{\mathrm {i}}}$ $r=r_{\mathrm {o} }$ r $= r$ $r=r_{\mathrm {o} }$ {\ $displaystyle$ $\nabla \times \mathbf {H} =0$ r $=r_{\mathrm {o$ 의 경계 조건을 고려합니다. $\nabla \times \mathbf {H} =0$ × $\nabla \times \mathbf {H} =0$ $=$ 0 {\ $displaystyle \times$ \times \ $mathbf {h}$ 의 $\nabla \times \mathbf {H} =0$ 작은 스트링 루프를 적용합니다.H $(\$ 의 $\mathbf{H}$ 병렬 성분이 연속적입니다.이를 위해서는 $\phi$ { $display$ $\phi$ style \ $phi$ }가 $\phi$ 경계에 걸쳐 연속적으로 존재해야 합니다.(더 정확하게는 $display$ { displaystyle \ $phi }$ 가 $\phi$ 경계에 걸쳐 일정하게 달라야 한다는 것을 의미하지만, 이 전위의 구배에 따라 관심이 있는 물리량이 달라지기 때문에 c에 대해 임의로 상수를 0으로 설정할 수 있습니다.불편함).두 번째 조건 세트를 얻으려면, 방정식 1을 경계를 가로지르는 작은 부피 전체에 통합하고 다음을 찾기 위해 발산 정리를 적용한다.

\left[{\frac {\partial \phi }{\partial r}}\right]=\pm \mathbf {M} \cdot {\hat {\mathbf {r} }}

\left[{\frac {\partial \phi }{\partial r}}\right]=\pm \mathbf {M} \cdot {\hat {\mathbf {r} }}

\left[{\frac {\partial \phi }{\partial r}}\right]=\pm \mathbf {M} \cdot {\hat {\mathbf {r} }}

]

=

± M

\left[{\frac {\partial \phi }{\partial r}}\right]=\pm \mathbf {M} \cdot {\hat {\mathbf {r} }}

r

^

{ \

displaystyle \ left

[ { \

frac \ phi }

{ \

right

]= \

pm

\

mathbf

{

M

} \

cdot

\

mathbf { r

}

}

,

여기서 $[f]$ [ $f]$ {displaystyle [ $f]$ 는 $[f]$ 경계를 가로지르는 $양$ f ${$ $displaystyle$ f $}$ 의 $f$ 점프를 나타내며, 이 경우 부호는 r $r=r_{\mathrm {i} }$ ${\mathrm {i}}}$ 에서 $r=r_{\mathrm {i} }$ 음수이고 r $=$ $r=r_{\mathrm {o} }$ $r=r_{\mathrm {o} }$ {\ $displaystyle$ r $=r_{\mathrm {o$ 에서 양수이다.부호 차이는 자화의 상대적인 방향과 실린더 벽 내부의 통합 부피 부분에 수직인 표면이 내부 및 외부 경계에서 반대이기 때문이다.

평면 극좌표에서 $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ F $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ + $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ $^$ $displaystyle \mathbf {F}$ = $F_{r} {\hat$ {\ $mathbf$ {r $}}$ + $F_$ {\ $theta$ } {\ $hat}$ {\ $boldsymbol$ {\ $ta$ }}}은 $\mathbf {F} =F_{r}{\hat {\mathbf {r} }}+F_{\theta }{\hat {\boldsymbol {\theta }}}$ 다음과 같이 주어진다.

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

=

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

r

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

∂

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

(

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

) +

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

r ∂

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

F θ

\nabla \cdot \mathbf {F} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rF_{r})+{\frac {1}{r}}{\frac {\partial F_{\theta }}{\partial \theta }}

θ

、

{

displaystyle

\

displayla

\

cdot

\

mathbf

{ F } =

scfrac {1} {r}

{\

frac

} {\ frac } {\

frac

（

R

_ r _ r

}

}

(3)

마찬가지로 스칼라 $필드$ f $\displaystyle$ f의 $f$ 구배는 다음과 같습니다.

\nabla f={\frac {\partial f}{\partial r}}{\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}{\hat {\boldsymbol {\theta }}}

bold

bold

f

\nabla f={\frac {\partial f}{\partial r}}{\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}{\hat {\boldsymbol {\theta }}}

^ +

\nabla f={\frac {\partial f}{\partial r}}{\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}{\hat {\boldsymbol {\theta }}}

r

\nabla f={\frac {\partial f}{\partial r}}{\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}{\hat {\boldsymbol {\theta }}}

f

bold

{

displaystyle

\

la

f

=

bold

frac

{

r }

{

\ frac

{

r

} + { \

frac

{

r

} { \

frac

} { \

theta

(4)

이 두 관계를 조합하면 라플라시안 $\nabla ^{2}f=\nabla \cdot (\nabla f)$ $\nabla ^{2}f=\nabla \cdot (\nabla f)$ $=$ ( ( ( $\nabla ^{2}f=\nabla \cdot (\nabla f)$ $\nabla ^{2}f=\nabla \cdot (\nabla f)$ ){ $display$ \ $scla ^{2}f$ =\ $scdot$ ( \ $scla$ f $\nabla ^{2}f=\nabla \cdot (\nabla f)$ )는 $\nabla ^{2}f=\nabla \cdot (\nabla f)$

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

f

=

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

r

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

(

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

) +

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

r 2

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

f

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂ 2 f

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

∂ 2 ∂ 2 ∂ 2 ∂ 2 ∂ 2 ∂

\nabla ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}}

2

displaydisplay

2

display

\ display

\ display

\

flac ^

{

r

} { \

frac

{ \

frac

} { \

frac

} { \ r } { \

lefrf r }

{ \ r

left

( r } { \

light

(

r （

r )

(5)

등식 3을 사용하여 실린더 벽의 자화 확산은 다음과 같다.

∇ ⋅ Mc는 yl=1r∂ ∂ r(rM0cos ⁡ θ)+1r∂ ∂ θ(M 0⁡ 이순신 θ))M 0 정해⁡ θ r+M 0 정해⁡ θ r)2M 0 정해⁡ θ r{\displaystyle{\begin{정렬}\nabla \cdot \mathbf{M}_{\mathrm{cyl}}&={\frac{1}{r}}{\frac{\partial}{r\partial}}(rM_{0}\cos.\theta

)+{\frac {1}{r}{\frac \theta

}}(

M_{0}\sin \theta)\&=

frac

{M_{0}\cos \theta }{r}+{\frac {M_{0}\

cos \

theta

}}}\

frac {\

ta =

frcs

\ta } {\ta } {\

ta

}

에 따라서 방정식 2, 그러니까 우리가 해결하고 싶다, 방정식을 5를 사용하여게 된다.

1r∂ ∂ r(r∂ ϕ ∂ r)+1r2∂ 2ϕ ∂ θ 2){0r<나는 − r2M 0 정해⁡ θ r나는 < r;r<>r o 0r>r0{\displaystyle{\frac{1}{r}}{\frac{\partial}{r\partial}}\left(r{\frac{\partial \phi}{\partial r}}\right)+{\frac{1}{r^{2}.}}{\frac{)부분 ^{2}\phi}{\partial\theta ^{2}}}=\left\{{\begin{행렬}0&, r<, r_{\mathrm{나는}}\\-{\frac{2M_{0}\cos\theta}{r}}&r_{\mathrm{나는}}<>r<, r_{\mathrm{는 o}}\\0&, r>, r_{\mathrm{0}}\end{매트릭스}}\right.}.

(6)

실린더 벽에서 이 방정식의 특정 해를 찾습니다. $\phi _{\mathrm {p} }=r\ln r\cos \theta$ 에 생각하면 p $\phi _{\mathrm {p} }=r\ln r\cos \theta$ $\phi _{\mathrm {p} }=r\ln r\cos \theta$ $\phi _{\mathrm {p} }=r\ln r\cos \theta$ cos $⁡display{\mathrm {p} =r\ln$ r $\cos \theta$ $\phi _{\mathrm {p} }=r\ln r\cos \theta$ 를 생각할 수 있습니다.그 이유는 다음과 같습니다.

\displaystyle {\frac {1} {r} {\frac r} {\frac r} {\frac r} {\mathrm {p} {\frac r} = {1} {\frac r} {\frac r} {\frac} {\frac r} \ left}\&=secfrac {cos \theta } {r} {\frac } {\sechr} \left [r(\ln r+1)\right] \\&=snfrac {cos \theta } {r}(\ln r+1+1)\\&=snfrac {\cos \theta } {r} + {\frac {2\cos \theta } {r}} \end {aligned}}

그리고 또

1r2∂ 2ϕ p∂ θ 2=1r2∂ 2∂ θ 2(rln ⁡ rcos ⁡ θ))− ln ⁡ r~왜냐면 ⁡θ r{\displaystyle{\begin{정렬}{\frac{1}{r^{2}}}{\frac{\partial ^{2}\phi _{\mathrm{p}}}{\partial\theta ^{2}}}&={\frac{1}{r^{2}}}{\frac{\partial ^{2}}{\partial\theta ^{2}}}(r\ln. r\co

s \theta

)

\\&=-{\frac {ln

r

\cos \theta

}{

r}}\end {aligned

따라서 $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ 2 $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ p $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ cos $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ \ $displaystyle$ \ $displayla$ ^ { $2$ } \ $phi$ _ { \ $mathrm$ { $p$ } = $display$ frac ${ 2$ \ $cos$ \ $theta$ } { $r$ } { r }} $\nabla ^{2}\phi _{\mathrm {p} }={\frac {2\cos \theta }{r}}$ = 식 6과의 비교 결과 - M $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ - $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ 0 $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ r $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ r ⁡ l ⁡ r $coscos$ 0 - $0$ - 0 $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ { { { { 0 - $-M_{0}\phi _{\mathrm {p} }=-M_{0}r\ln r\cos \theta$ { { { 0 { 0 { 0 { 。

이제 방정식 6의 균질 방정식을 생각해 봅시다. 즉, $\nabla ^{2}\phi _{\mathrm {h} }=0$ $\nabla ^{2}\phi _{\mathrm {h} }=0$ h $\nabla ^{2}\phi _{\mathrm {h} }=0$ \ $displaystyle$ \ $displayla$ ^{ $2}\phi$ _ ${\mathrm {h}$ = $0$ 입니다.이것은 라플라스 방정식의 형태를 가지고 있다.변수 분리 방법을 통해 구배가 $\theta$ 인 (모든 물리량이 단일값인 $)$ $일반적$ 인 균질해는 다음과 같이 나타낼 수 있다.

、

}\theta

+

C_{

0}\

ln

r+\

sum _{n=

1}^{\infty

}\left(A_{n}r^{n

}+

B_{n}r^{-n}\right)\cos

n

\theta +\sum _{n=

1}^{\infty

}\

lefty }\

lefty_{n

}\lefti }

여기서 $A_{i},\ B_{i},\ C_{i},\ D_{i}$ $A_{i},\ B_{i},\ C_{i},\ D_{i}$ $A_{i},\ B_{i},\ C_{i},\ D_{i}$ $(\$ 는 $A_{i},\ B_{i},\ C_{i},\ D_{i}$ 임의의 상수입니다.원하는 솔루션은 경계 조건을 충족하는 특정 및 균질 솔루션의 합계가 될 것이다.다시 한 번, 나중에 생각해보면, 대부분의 상수를 즉시 0으로 설정하고 해답이 다음과 같다고 주장하자.

ϕ){α r~왜냐면, 나는 − r데다 ⁡ θ β rθ r<>⁡ M 0rln ⁡ r~왜냐면 ⁡θ r나는 &lt하며<>r o 0r>r o{\displaystyle\phi =\left\{{\begin{행렬}\alpha r\cos\theta&r<, r_{\mathrm{나는}}\\\beta r\cos -M_{0}r\ln r\cos\theta 및 \theta, r_{\mathrm{나는}}<>r<, r_{\mathrm{는 o}}\\0&, r>r_{\mathrm{는 o}}\end{매트릭스}}\right.}

\phi =\left\{{\begin{matrix}\alpha r\cos \theta &r<r_{\mathrm {i} }\\\beta r\cos \theta -M_{0}r\ln r\cos \theta &r_{\mathrm {i} }<r<r_{\mathrm {o} }\\0&r>r_{\mathrm {o} }\end{matrix}}\right.

,

$\alpha ,\ \beta$ 서 $\alpha ,\ \beta$ β(\ $displaystyle \alpha,\displays }$ 는 $\alpha ,\ \beta$ 결정되는 상수입니다.만약 우리가 경계 조건이 충족되도록 상수를 선택할 수 있다면, 포아송 방정식의 고유성 정리에 의해 우리는 해답을 찾은 것이 틀림없다.

연속성 조건에 따라 다릅니다.

\alpha =\displays - M_{0}\ln r_{\mathrm {i}}

(7)

안쪽 경계에

\displaystyle -M_{0}\ln r_{\mathrm {o} = 0}

(8)

바깥 경계에 있습니다.전위 $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ 는 실린더 $\alpha \cos \theta$ 과 $\alpha \cos \theta$ cos $\alpha \cos \theta$ - $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ r cos $\alpha \cos \theta$ $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ - M 0 $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ cos $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ - $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ 0 cos $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ display $\alpha \cos \theta$ $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ （ \ $displaystyle \beta \cos \theta$ - $M_{0}\ln$ r $\cos$ \ $theta$ \cos \ $cs$ $\beta \cos \theta -M_{0}\ln r\cos \theta -M_{0}\cos \theta$ \cos \cs \cs \cos \cos \ta \cos \cos \cos \cos \cos \cos \cos \cos \cseta $\alpha \cos \theta$ \ $cos$ \cos \ta \cseta \ $\alpha \cos \theta$

\displaystyle (\cos \cos \theta - M_{0}\ln r_{i}\cos \theta - M_{0}\cos \theta \cos \cos \cos \cos \ta \m_{0}\ln r_{i})-\alpha \ta \cos \cos \cos \cos \cos \cseta \ta \ta \ta \ta - M_{0}

안쪽 경계에

\displaystyle 0-(\cos \theta - M_{0}\ln r_{\mathrm {0}\cos \theta )=M_{0}\cos \theta \cos \cs - M_{0}\ln r_{\mathrmo} =0}

바깥 경계에 있습니다.이것들은 식 7과 식 8과 동일하기 때문에 추측은 일관성이 있습니다.따라서 $\beta =M_{0}\ln r_{\mathrm {o} }$ $=$ M $\beta =M_{0}\ln r_{\mathrm {o} }$ $\beta =M_{0}\ln r_{\mathrm {o} }$ {\ $displaystyle$ \ $displaystyle$ $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ = $M_$ ${$ 0 $}\$ $ln r_{\mathrm$ { $o$ $}}}$ 및 α = M 0 ln $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ （ $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ ） { $\alpha =M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)$ \ $alpha = M_{0}\ln$ { $rmathrm$ { $rm}$ {rm} {rm} { $rm}$ 이 있습니다 $.$

\phi =\left\{{\begin{matrix}M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)r\cos \theta &r<r_{\mathrm {i} }\\M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)r\cos \theta &r_{\mathrm {i} }<r<r_{\mathrm {o} }\\0&r>r_{\mathrm {o} }\end{matrix}}\right.

M_{0}\ln \left({\frac {r_{\mathrm {o}}}) {r_{\mathrm {i}}}\right) r\cos \theta &r <r_{\mathrm {i}}\ln \left({\frac {\mathrecr}}\right}}}}}})

\phi =\left\{{\begin{matrix}M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)r\cos \theta &r<r_{\mathrm {i} }\\M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)r\cos \theta &r_{\mathrm {i} }<r<r_{\mathrm {o} }\\0&r>r_{\mathrm {o} }\end{matrix}}\right.

그 결과, 자기장은 다음과 같이 주어진다.

H)∇ϕ={M 0;r 나는 M 0 정해⁡ θ[ln ⁡(r거예요 r)− 1]r^(M 0ln ⁡(r거예요 r)sin ⁡ θθ ^ 나는 < r;r<>r o 0r을⁡(r거예요 r나는). 왜냐하면⁡ θ r^(M 0ln ⁡(r거예요 r나는)sin ⁡ θθ ^ r<>ln;r o

\mathbf {H} =\displayla \phi =\left\{\display{H

M_{0}\ln \left({\frac{r_{\mathrm{시}}}{r_{\mathrm{나는}}}}\right)\cos(\,{\hat{\mathbf{r}}}-M_{0}\ln \left({\frac{r_{\mathrm{시}}}{r_{\mathrm{나는}}}}\right)\sin \theta \,{\hat{\boldsymbol{\theta}}}&r<, r_{\mathrm{나는}}\\M_{0}\cos(\left[\ln \left시({\frac{r_{\mathrm{}}}{r}}\right)-1\right]\,{\hat{\mathbf{r}}}-M_{0}\ln.\left(

{\frac {r_{\mathrm {o}}}{r}}\sin \theta

},

{\hat

{

boldsymbol {theta

}&

r_{\mathrm {o}}\0&r> r_{\mathrm {o}\end{\h}},

{\hat

},

right

\mathbf {H} =\nabla \phi =\left\{{\begin{matrix}M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)\cos \theta \,{\hat {\mathbf {r} }}-M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)\sin \theta \,{\hat {\boldsymbol {\theta }}}&r<r_{\mathrm {i} }\\M_{0}\cos \theta \left[\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)-1\right]\,{\hat {\mathbf {r} }}-M_{0}\ln \left({\frac {r_{\mathrm {o} }}{r}}\right)\sin \theta \,{\hat {\boldsymbol {\theta }}}&r_{\mathrm {i} }<r<r_{\mathrm {o} }\\0&r>r_{\mathrm {o} }\end{matrix}}\right.

자속 밀도는 이전 $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ B = $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ 0 ( $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ $\mathbf {B} =\mu _{0}(\mathbf {H} +\mathbf {M} )$ $)$ { $displaystyle \mathbf {B}$ =\ $mu$ _ ${0}(\mathbf {H} +\mathbf {M$ 을 사용하여 어디에서나 찾을 수 있지만, 보어에서는 자속이 사라지는 B $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ 0 $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ 로 $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ 합니다. ${param}$ } $= param frac {$ 1} ${\mu$ _ ${0}}\mathbf$ {H} $_{\mathrm$ {param $\mathbf {B} _{\mathrm {bore} }={\frac {1}{\mu _{0}}}\mathbf {H} _{\mathrm {bore} }$ 따라서 플럭스 밀도의 크기는 다음과 같습니다.

B_{\mathrm {bore} }=\left|\mathbf {B} _{\mathrm {bore} }\right|={\sqrt {\cos ^{2}\theta +\sin ^{2}\theta }}{\frac {M_{0}}{\mu _{0}}}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)={\frac {M_{0}}{\mu _{0}}}\ln \left({\frac {r_{\mathrm {o} }}{r_{\mathrm {i} }}}\right)

ftbc\frac {r_

{\

mathrm

{o

}}}}{r_{\mathrm

{

i}}}\right)=bln frac

{

M_{0}{\mathrm {o}}}}{r_{\right

위치와는 무관합니다.마찬가지로 실린더 외부에서는 자화도 사라지며, 거기서 자기장이 사라지기 때문에 플럭스 밀도도 사라집니다.즉, 이 장은 실제로 물리적 치수에 따라 크기가 달라지고 이상적인 할바흐 원통 밖에서는 0이 됩니다.

필드 변경

Halbach 실린더는 정적 필드를 생성합니다.그러나 실린더를 네스트할 수 있고 한쪽 실린더를 다른 쪽 실린더에 대해 회전시킴으로써 필드 취소 및 방향 조정을 실현할 ^[21]수 있다.실린더의 외부 자기장이 매우 낮기 때문에 상대 회전은 강한 힘을 필요로 하지 않는다.무한히 긴 실린더의 이상적인 경우, 실린더를 다른 실린더에 대해 회전시키는 데 힘이 필요하지 않습니다.

평면 할바흐 어레이와 동심원 구조 권선을 이용한 자기 부상

구

할바흐 실린더의 2차원 자기분포 패턴을 3차원까지 연장하면 할바흐 구가 된다.이러한 설계는 유한 길이 실린더 설계에서 일반적인 "끝 효과"의 영향을 받지 않기 때문에 설계 내부에는 매우 균일한 필드가 있습니다.구체의 균일한 필드의 크기는 또한 동일한 내부 반지름과 외부 반지름을 가진 이상적인 원통 설계의 4/3까지 증가한다.그러나 구면 구조의 경우 균일한 필드 영역에 대한 접근은 일반적으로 설계의 상단과 하단의 좁은 구멍으로 제한됩니다.

할바흐 구체의^[22] 장 방정식은 다음과 같다.

({displaystyle B=bcfrac {4}{3}}B_{0}\ln \leftfrac {R_{\text{o}}}{R_{\text{i}}}}\right).}

구형 설계가 (선 쌍극자가 아닌) 점 쌍극자로 구성된다는 사실을 고려하도록 최적화함으로써 더 높은 필드가 가능합니다.그 결과 구체가 타원 모양으로 늘어나며 구성 요소 전체에 걸쳐 자화가 불균일하게 분포됩니다.설계 내의 연성 극 조각뿐만 아니라 이 방법을 사용하여 1998년 ^[23]Bloch 등에 의해 20mm의³ 작업 부피의 4.5T가 달성되었고,^[24] 이는 0.05mm의³ 더 작은 작업 부피에도 불구하고 2002년에 5T로 더 증가하였다.경질 재료는 온도에 의존하기 때문에 Kumada 등에서도 알 수 있듯이 마그네트 어레이 전체를 냉동하면 작업 영역 내에서 자기장이 더욱 커질 수 있다.이 그룹은 ^[25]또한 2003년에 5.16T 할바흐 쌍극자 실린더의 개발을 보고했다.

「」를 참조해 주세요.

초자석
영구 자석
집중력이 강하다
인덕트랙은 Halbach 어레이를 사용하여 자기부상용으로 강력한 필드를 생성합니다.
헬름홀츠 코일은 매우 고른 자기장을 제공할 수 있습니다.

레퍼런스

^ Klaus Halbach (1980). "Design of permanent multipole magnets with oriented rare earth cobalt material" (PDF). Nuclear Instruments and Methods. 169 (1): 1–10. Bibcode:1980NucIM.169....1H. doi:10.1016/0029-554X(80)90094-4. ISSN 0029-554X.
^ Klaus Halbach (1985). "Applications of Permanent Magnets in Accelerators and Electron Storage Rings" (PDF). Journal of Applied Physics. 57 (1): 3605–3608. Bibcode:1985JAP....57.3605H. doi:10.1063/1.335021. ISSN 0029-554X.
^ "Electromagnetic Transducer, James Winey, Figure 29; United States Patent 3,674,946, filed Dec. 23, 1970". www.espacenet.com.
^ Mallinson J.C. (1973). "One-Sided Fluxes — A Magnetic Curiosity?". IEEE Transactions on Magnetics. 9 (4): 678–682. Bibcode:1973ITM.....9..678M. doi:10.1109/TMAG.1973.1067714.
^ "Magnetically levitated train takes flight US Department of Energy Science News EurekAlert! Science News". www.eurekalert.org.
^ Creel, James R. (2006). "Concerning the Physics of Halbach Arrays". Archived from the original on 4 June 2011. Retrieved 31 August 2008.
^ "High efficiency voice coil motor".
^ A. Sarwar; A. Nemirovski; B. Shapiro (2012). "Optimal Halbach permanent magnet designs for maximally pulling and pushing nanoparticles" (PDF). Journal of Magnetism and Magnetic Materials. 324 (5): 742–754. Bibcode:2012JMMM..324..742S. doi:10.1016/j.jmmm.2011.09.008. PMC 3547684. PMID 23335834.
^ Richard F. Post (10 October 2005). "Toward More Efficient Transport: The Inductrack Maglev System" (PDF). Lawrence Livermore National Laboratory. Retrieved 1 December 2017.
^ L. S. Tung; R. F. Post; J. Martinez-Frias (27 June 2001). "Final progress report for the NASA Inductrack model rocket launcher at the Lawrence Livermore National Laboratory" (PDF). UCRL-ID-144455. Archived from the original (PDF) on 5 March 2016. Retrieved 12 January 2016. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ J. E. Hilton; S. M. McMurry (2012). "An adjustable linear Halbach array" (PDF). Journal of Magnetism and Magnetic Materials. 324 (13): 2051–2056. Bibcode:2012JMMM..324.2051H. doi:10.1016/j.jmmm.2012.02.014. hdl:2262/63909.
^ T. R. Ni Mhiochain; D. Weaire; S. M. McMurry; J. M. D. Coey (1999). "Analysis of torque in nested magnetic cylinders". Journal of Applied Physics. 86 (11): 6412–6424. Bibcode:1999JAP....86.6412N. doi:10.1063/1.371705.
^ R. Bjørk (2011). "The ideal dimensions of a Halbach cylinder of finite length". Journal of Applied Physics. 109 (1): 013915–013915–6. arXiv:1410.0496. Bibcode:2011JAP...109a3915B. doi:10.1063/1.3525646. S2CID 119168717.
^ R. Bjørk; A. Smith; C. R. H. Bahl (2010). "Analysis of the magnetic field, force, and torque for two-dimensional Halbach cylinders" (PDF). Journal of Magnetism and Magnetic Materials. 322 (1): 133–141. arXiv:1409.1712. Bibcode:2010JMMM..322..133B. doi:10.1016/j.jmmm.2009.08.044. S2CID 56325133.
^ R. Bjørk; A. Smith; C. R. H. Bahl (2015). "The efficiency and the demagnetization field of a general Halbach cylinder" (PDF). Journal of Magnetism and Magnetic Materials. 384: 128–132. arXiv:1502.06700. Bibcode:2015JMMM..384..128B. doi:10.1016/j.jmmm.2015.02.034. S2CID 54826296.
^ A. R. Insinga; C. R. H. Bahl; R. Bjørk; A. Smith (2016). "Performance of Halbach magnet arrays with finite coercivity". Journal of Magnetism and Magnetic Materials. 407: 369–376. Bibcode:2016JMMM..407..369I. doi:10.1016/j.jmmm.2016.01.076. S2CID 124300587.
^ J. M. D. Coey; T.R. Ní Mhíocháin (2003). "Permanent Magnets". In F. Herlach; N. Miura (eds.). High Magnetic Fields: Science and Technology. Vol. 1. World Scientific Publishing. pp. 25–47. ISBN 978-981-02-4964-9.
^ O. Cugat; F. Bloch; J.C. Toussaint (1998). "4-Tesla Permanent Magnetic Flux Source". Proc. 15th International Workshop on Rare Earth Magnets and Their Applications: 807.
^ Raich, H., Blümler, P. (21 October 2004). "Design and construction of a dipolar Halbach array with a homogeneous field from identical bar magnets: NMR Mandhalas". Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 23B: 16–25. doi:10.1002/cmr.b.20018.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)
^ Fitzpatrick, Richard (27 June 2014). "Uniformly Magnetized Sphere". The University of Texas at Austin. Retrieved 28 March 2022.
^ "Tip Magazine: Magnets, Markets, and Magic Cylinders The Industrial Physicist by Michael Coey and Denis Weaire" (PDF). Archived from the original (PDF) on 28 March 2006.
^ 영구 자석 기반 자기장 소스.
^ Bloch, F. and Cugat, O. and Meunier, G. and Toussaint, J.C. (1998). "Innovating approaches to the generation of intense magnetic fields: design and optimization of a 4 Tesla permanent magnet flux source". IEEE Transactions on Magnetics. 34 (5): 2465–2468. Bibcode:1998ITM....34.2465B. doi:10.1109/20.717567.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ "Record-breaking magnet has five-tesla field". CERN Courier. 22 March 2002.
^ Kumada, M. and Antokhin, E.I. and Iwashita, Y. and Aoki, M. and Sugiyama, E. (2004). "Super Strong Permanent Magnet Quadrupole for a Linear Collider" (PDF). IEEE Transactions on Applied Superconductivity. 14 (2): 1287–1289. Bibcode:2004ITAS...14.1287K. doi:10.1109/TASC.2004.830555. S2CID 23698444.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

외부 링크

[Halbach1980-1] Klaus Halbach (1980). "Design of permanent multipole magnets with oriented rare earth cobalt material" (PDF). Nuclear Instruments and Methods. 169 (1): 1–10. Bibcode:1980NucIM.169....1H. doi:10.1016/0029-554X(80)90094-4. ISSN 0029-554X.

[Halbach1985-2] Klaus Halbach (1985). "Applications of Permanent Magnets in Accelerators and Electron Storage Rings" (PDF). Journal of Applied Physics. 57 (1): 3605–3608. Bibcode:1985JAP....57.3605H. doi:10.1063/1.335021. ISSN 0029-554X.

[3] "Electromagnetic Transducer, James Winey, Figure 29; United States Patent 3,674,946, filed Dec. 23, 1970". www.espacenet.com.

[4] Mallinson J.C. (1973). "One-Sided Fluxes — A Magnetic Curiosity?". IEEE Transactions on Magnetics. 9 (4): 678–682. Bibcode:1973ITM.....9..678M. doi:10.1109/TMAG.1973.1067714.

[5] "Magnetically levitated train takes flight US Department of Energy Science News EurekAlert! Science News". www.eurekalert.org.

[6] Creel, James R. (2006). "Concerning the Physics of Halbach Arrays". Archived from the original on 4 June 2011. Retrieved 31 August 2008.

[7] "High efficiency voice coil motor".

[Sarwar2012-8] A. Sarwar; A. Nemirovski; B. Shapiro (2012). "Optimal Halbach permanent magnet designs for maximally pulling and pushing nanoparticles" (PDF). Journal of Magnetism and Magnetic Materials. 324 (5): 742–754. Bibcode:2012JMMM..324..742S. doi:10.1016/j.jmmm.2011.09.008. PMC 3547684. PMID 23335834.

[9] Richard F. Post (10 October 2005). "Toward More Efficient Transport: The Inductrack Maglev System" (PDF). Lawrence Livermore National Laboratory. Retrieved 1 December 2017.

[Tung2001-10] L. S. Tung; R. F. Post; J. Martinez-Frias (27 June 2001). "Final progress report for the NASA Inductrack model rocket launcher at the Lawrence Livermore National Laboratory" (PDF). UCRL-ID-144455. Archived from the original (PDF) on 5 March 2016. Retrieved 12 January 2016. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[Hilton2012-11] J. E. Hilton; S. M. McMurry (2012). "An adjustable linear Halbach array" (PDF). Journal of Magnetism and Magnetic Materials. 324 (13): 2051–2056. Bibcode:2012JMMM..324.2051H. doi:10.1016/j.jmmm.2012.02.014. hdl:2262/63909.

[Mhiochain1999-12] T. R. Ni Mhiochain; D. Weaire; S. M. McMurry; J. M. D. Coey (1999). "Analysis of torque in nested magnetic cylinders". Journal of Applied Physics. 86 (11): 6412–6424. Bibcode:1999JAP....86.6412N. doi:10.1063/1.371705.

[Bjoerk2011-13] R. Bjørk (2011). "The ideal dimensions of a Halbach cylinder of finite length". Journal of Applied Physics. 109 (1): 013915–013915–6. arXiv:1410.0496. Bibcode:2011JAP...109a3915B. doi:10.1063/1.3525646. S2CID 119168717.

[Bjoerk2010-14] R. Bjørk; A. Smith; C. R. H. Bahl (2010). "Analysis of the magnetic field, force, and torque for two-dimensional Halbach cylinders" (PDF). Journal of Magnetism and Magnetic Materials. 322 (1): 133–141. arXiv:1409.1712. Bibcode:2010JMMM..322..133B. doi:10.1016/j.jmmm.2009.08.044. S2CID 56325133.

[Bjoerk2015-15] R. Bjørk; A. Smith; C. R. H. Bahl (2015). "The efficiency and the demagnetization field of a general Halbach cylinder" (PDF). Journal of Magnetism and Magnetic Materials. 384: 128–132. arXiv:1502.06700. Bibcode:2015JMMM..384..128B. doi:10.1016/j.jmmm.2015.02.034. S2CID 54826296.

[Insinga2016-16] A. R. Insinga; C. R. H. Bahl; R. Bjørk; A. Smith (2016). "Performance of Halbach magnet arrays with finite coercivity". Journal of Magnetism and Magnetic Materials. 407: 369–376. Bibcode:2016JMMM..407..369I. doi:10.1016/j.jmmm.2016.01.076. S2CID 124300587.

[Coey2003-17] J. M. D. Coey; T.R. Ní Mhíocháin (2003). "Permanent Magnets". In F. Herlach; N. Miura (eds.). High Magnetic Fields: Science and Technology. Vol. 1. World Scientific Publishing. pp. 25–47. ISBN 978-981-02-4964-9.

[Cugat1998-18] O. Cugat; F. Bloch; J.C. Toussaint (1998). "4-Tesla Permanent Magnetic Flux Source". Proc. 15th International Workshop on Rare Earth Magnets and Their Applications: 807.

[19] Raich, H., Blümler, P. (21 October 2004). "Design and construction of a dipolar Halbach array with a homogeneous field from identical bar magnets: NMR Mandhalas". Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering. 23B: 16–25. doi:10.1002/cmr.b.20018.{{cite journal}}: CS1 maint: 작성자 파라미터 사용(링크)

[20] Fitzpatrick, Richard (27 June 2014). "Uniformly Magnetized Sphere". The University of Texas at Austin. Retrieved 28 March 2022.

[21] "Tip Magazine: Magnets, Markets, and Magic Cylinders The Industrial Physicist by Michael Coey and Denis Weaire" (PDF). Archived from the original (PDF) on 28 March 2006.

[22] 영구 자석 기반 자기장 소스.

[Bloch1998-23] Bloch, F. and Cugat, O. and Meunier, G. and Toussaint, J.C. (1998). "Innovating approaches to the generation of intense magnetic fields: design and optimization of a 4 Tesla permanent magnet flux source". IEEE Transactions on Magnetics. 34 (5): 2465–2468. Bibcode:1998ITM....34.2465B. doi:10.1109/20.717567.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[24] "Record-breaking magnet has five-tesla field". CERN Courier. 22 March 2002.

[Kumada2004-25] Kumada, M. and Antokhin, E.I. and Iwashita, Y. and Aoki, M. and Sugiyama, E. (2004). "Super Strong Permanent Magnet Quadrupole for a Linear Collider" (PDF). IEEE Transactions on Applied Superconductivity. 14 (2): 1287–1289. Bibcode:2004ITAS...14.1287K. doi:10.1109/TASC.2004.830555. S2CID 23698444.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[1]

[2]

[3]

[4]

[5]

[6]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

Search

할바흐 어레이

네임스페이스

더

목차

선형 어레이

자화

적용들

리니어

★★★★★★★★★★★★★★★★★」

프로그램

한 필드

인

필드 변경

구

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

할바흐 어레이

선형 어레이

자화

적용들

리니어

★★★★★★★★★★★★★★★★★」

프로그램

한 필드

인

필드 변경

구

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.