트러스
Truss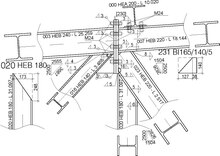
트러스란 견고한 구조를 만드는 보와 같은 부재의 집합체이며, [1]노드로 연결됩니다.
공학에서 트러스란 "2개의 힘 부재로만 구성되며, 부재는 집합체가 전체적으로 단일 개체로 동작하도록 구성되어 있다"[2]는 구조이다."2-힘 부재"는 힘이 두 지점에만 적용되는 구조 구성요소이다.이 엄격한 정의를 통해 부재가 안정된 구성으로 연결된 형상을 가질 수 있지만 트러스에는 일반적으로 5개 이상의 삼각 유닛이 있으며, 이들 유닛의 끝은 노드라고 불리는 조인트로 연결되어 있습니다.
이 전형적인 맥락에서, 외부 힘과 그러한 힘에 대한 반응은 노드에서만 작용하는 것으로 간주되며, 인장 또는 압축된 부재의 힘을 발생시킨다.직선 부재의 경우 모멘트(토크)는 명시적으로 제외됩니다.이는 트러스 내의 모든 조인트가 2개의 힘 부재가 되기 위해 필요한 회전으로 취급되기 때문입니다.
평면 트러스란 모든 부재와 노드가 2차원 평면 내에 있는 반면 공간 트러스에는 3차원으로 확장되는 부재와 노드가 있습니다.트러스에서 상단 보를 상단 현이라고 하며 일반적으로 압축 상태이고 하단 보를 하단 현이라고 하며 일반적으로 장력 상태입니다.내부 빔을 웹이라고 하고 웹 내부의 영역을 [3]패널 또는 그래픽 스태틱스(Cremona 다이어그램 참조) 폴리곤이라고 합니다.[4]
어원학
트러스(Truss)는 고대 프랑스어 truse에서 유래한 말로, 1200년 경에 "함께 묶인 것들의 집합"[5][6]을 뜻한다.트러스라는 용어는 종종 크럭[7][8] 프레임이나 [9][10]서까래와 같은 부재의 조립을 나타내는 데 사용됩니다.한 가지 공학적 정의는 "트러스는 먼 거리를 가로지르기 위해 일련의 삼각형[sic]을 형성하는 각각의 구조 부재[sic]의 끝부분이 연결된 단일 평면 프레임워크입니다."[11]
특성.
트러스(trus)는 일반적으로 접합부에 연결된 직선 부재(반드시 그렇지는 않음)로 구성됩니다. 이 부재는 일반적으로 패널 점이라고 합니다.트러스(Trus)는 일반적으로 삼각형으로 구성됩니다(반드시[12] 그렇지는 않습니다). 이 모양과 설계의 구조적 안정성 때문입니다.삼각형은 변의 길이가 [13]고정되어도 모양이 변하지 않는 가장 단순한 기하학적 도형입니다.이에 비해 사각형은 각도와 길이가 모두 고정되어 있어야 모양을 유지할 수 있다.트러스가 지지되도록 설계된 조인트를 일반적으로 먼터 [citation needed]점이라고 합니다.
심플 트러스

트러스의 가장 단순한 형태는 하나의 삼각형이다.이러한 트러스 유형은 서까래와 천장 [14]받침으로 구성된 프레임 지붕과 자전거 및 항공기 같은 다른 기계 구조에서 볼 수 있습니다.이 형상의 안정성과 그 안의 힘을 계산하는 데 사용되는 분석 방법 때문에, 완전히 삼각형으로 구성된 트러스(trus)[15]는 단순 트러스(simple trus)라고 합니다.단, 단순 트러스란 각각 기존 2개의 접합부에 연결되고 새로운 접합부를 형성하기 위해 서로 연결된 한 쌍의 부재를 연속적으로 추가하여 시공할 수 있도록 요구함으로써 보다 제한적으로 정의되는 경우가 많으며,[12] 이 정의는 단순 트러스만으로 구성될 필요가 없다.두 개의 삼각형을 연결한 전통적인 다이아몬드 모양의 자전거 프레임은 단순한 [16]트러스입니다.
평면 트러스
평면 트러스는 단일 [15]평면에 있습니다.평면 트러스는 일반적으로 지붕과 [17]교량을 형성하기 위해 병렬로 사용됩니다.
트러스의 깊이 또는 상현과 하현 사이의 높이가 트러스 구조를 효율적으로 만듭니다.동일한 강도를 가진 고체 거더 또는 보는 트러스 대비 상당한 무게 및 재료 비용을 가집니다.지정된 스팬에서 트러스가 깊을수록 현에 필요한 재료는 줄어들고 수직 및 대각선에 더 많은 재료가 필요합니다.트러스 깊이의 최적화는 효율을 [18]극대화할 것이다.
공간 프레임 트러스
공간 프레임 트러스란 끝부분에 핀으로 고정된 부재의 3차원 구조입니다.사면체 모양은 가장 단순한 공간 트러스이며, 4개의 [15]조인트에서 만나는 6개의 부재로 구성됩니다.대형 평면구조는 공통 가장자리를 가진 사면체로 구성될 수 있으며, 또한 대형 독립 전력선 주탑의 베이스 구조에도 사용된다.
이 주탑은 3차원 트러스 구조입니다.
종류들
- 트러스 유형은 교량에 사용되는 트러스 유형을 참조하십시오.

트러스에는 기본적으로 두 가지 유형이 있습니다.
- 피치 트러스 또는 공통 트러스(common trus)는 삼각형 모양으로 특징지어집니다.그것은 지붕 공사에 가장 많이 사용된다.일부 일반적인 트러스에는 "웹 구성"에 따라 이름이 지정됩니다.코드 크기와 웹 구성은 스판, 하중 및 간격에 따라 결정됩니다.
- 평행현 트러스 또는 플랫트러스는 평행한 상단 및 하단 현에서 이름을 얻습니다.그것은 바닥 공사에 자주 사용된다.
두 가지 조합은 힙 루프 구조에 사용되는 잘린 트러스입니다.금속판 연결 목재 트러스란 나무 부재가 금속 커넥터 플레이트로 연결된 지붕 또는 바닥 트러스입니다.
워렌 트러스
트러스 부재는 위아래로 번갈아 가면서 일련의 정삼각형을 형성합니다.
옥텟 트러스
트러스 부재는 모든 등변 삼각형으로 구성됩니다.최소 구성은 8면체와 함께 두 개의 정사면체이다.다양한 구성으로 3차원 공간을 채웁니다.
프랫 트러스
![]() 프랫 트러스는 1844년 두 명의 보스턴 철도 엔지니어 [19]케일럽 프랫과 그의 아들 토마스 윌리스 [20]프랫에 의해 특허를 받았다.이 디자인은 수직 부재를 압축에 사용하고 대각 부재를 사용하여 장력에 반응합니다.프랫 트러스 디자인은 교량 설계자가 나무에서 철로, 그리고 철에서 [21]강철로 바뀌면서 인기를 유지했습니다.이러한 Pratt Trus의 지속적인 인기는 아마도 부재의 구성이 더 긴 대각 부재가 중력 하중 효과에만 장력이 있다는 것을 의미하기 때문일 것이다.압축하중에서의 좌굴과 관련된 슬렌더니스 효과(부재의 길이에 의해 복합됨)는 일반적으로 설계를 제어하지 않기 때문에 이러한 부재를 보다 효율적으로 사용할 수 있다.따라서 고정된 깊이의 평면 트러스의 경우 일반적으로 정적 수직 하중에서 Pratt 구성이 가장 효율적입니다.
프랫 트러스는 1844년 두 명의 보스턴 철도 엔지니어 [19]케일럽 프랫과 그의 아들 토마스 윌리스 [20]프랫에 의해 특허를 받았다.이 디자인은 수직 부재를 압축에 사용하고 대각 부재를 사용하여 장력에 반응합니다.프랫 트러스 디자인은 교량 설계자가 나무에서 철로, 그리고 철에서 [21]강철로 바뀌면서 인기를 유지했습니다.이러한 Pratt Trus의 지속적인 인기는 아마도 부재의 구성이 더 긴 대각 부재가 중력 하중 효과에만 장력이 있다는 것을 의미하기 때문일 것이다.압축하중에서의 좌굴과 관련된 슬렌더니스 효과(부재의 길이에 의해 복합됨)는 일반적으로 설계를 제어하지 않기 때문에 이러한 부재를 보다 효율적으로 사용할 수 있다.따라서 고정된 깊이의 평면 트러스의 경우 일반적으로 정적 수직 하중에서 Pratt 구성이 가장 효율적입니다.
애리조나주 템페에 있는 서던 퍼시픽 철교는 1912년에 [22][23]건설된 393미터의 트러스 다리이다.이 구조는 길이가 다양한 9개의 Pratt 트러스 스팬으로 구성됩니다.그 다리는 오늘날에도 여전히 사용되고 있다.
Wright Flyer는 압축 부재 길이를 최소화하여 공기역학적 저항을 [24]줄일 수 있도록 날개 구조에 Pratt 트러스(트러스)를 사용했습니다.
보스트링 트러스
그 모양 때문에 이름이 붙여진 활줄 트러스(bowstring truss)는 종종 묶인 아치형 다리와 혼동되는 아치형 트러스 교량에 처음 사용되었습니다.
제2차 세계대전 동안 수천 개의 활줄 트러스들이 항공기 격납고와 다른 군용 건물의 곡면 지붕을 지탱하는 데 사용되었다.거의 이등변삼각형에서 프랫트러스의 변형에 이르기까지 상부 호의 노드와 하부 직선 계열의 부재의 노드를 연결하는 부재의 배열에는 많은 변화가 존재한다.
킹 포스트 트러스
가장 간단한 트러스 스타일 중 하나인 킹 포스트는 공통 수직 지지대로 기울어진 두 개의 각진 지지대로 구성됩니다.
퀸 포스트 트러스(때로는 퀸 포스트 또는 퀸 포스트)는 외부 지지대가 구조물의 중앙을 향해 기울어져 있다는 점에서 킹 포스트 트러스(King Post Trus)와 유사합니다.주된 차이점은 중앙의 수평 익스텐션이며, 빔의 작용에 의존하여 기계적 안정성을 제공합니다.이 트러스 스타일은 비교적 짧은 [25]스팬에만 적합합니다.
렌즈 트러스
1878년 윌리엄 더글러스에 의해 특허 취득된 렌티큘러 트러스는 (1823년의 다리가 최초의 형태이긴 하지만) 트러스 상부와 하부의 현을 아치형으로 하여 렌즈 모양을 형성합니다.렌티큘러 포니 트러스 교량은 노반 위아래로 뻗은 렌티큘러 트러스 교량 설계입니다.
마을의 격자 트러스
미국의 건축가 Ithiel Town은 무거운 나무 다리의 대안으로 타운의 래티스 트러스를 디자인했습니다.1820년과 1835년에 특허를 받은 그의 디자인은 짧은 간격을 두고 대각선으로 배열된 다루기 쉬운 판자를 사용하여 격자를 형성한다.
비에렌델 트러스

비에렌델 트러스란 부재가 삼각형이 아닌 직사각형 개구부를 형성한 구조로 굽힘 모멘트를 전달하고 저항할 수 있는 고정 접합부가 있는 프레임이다.따라서 트러스(비2포스 부재 포함)의 엄격한 정의에 부합하지 않습니다.일반 트러스에는 일반적으로 핀 조인트가 있는 것으로 간주되는 부재로 구성되며, 이는 접합된 단부에 모멘트가 존재하지 않는다는 것을 의미합니다.이 건축양식은 1896년에 이 디자인을 개발한 벨기에의 기술자 Arthur Vierendeel의 [26]이름을 따서 지어졌다.삼각 트러스보다 비용이 높아 교량 용도로 사용하는 경우는 드물다.
건물에서 이러한 유형의 구조물은 많은 양의 외부 외피가 방해되지 않고 창문과 문 개구부에 사용될 수 있다는 것이 효용이다.일부 용도에서는 대각선 가새로 인해 일부 영역이 막히는 브레이스 프레임 시스템보다 이 방법이 선호됩니다.
스태틱스
핀 조인트(pin joint)에 의해 연결되고 힌지 조인트(hinged joint)와 롤러(roller)에 의해 양단에서 지지되는 부재로 구성된 트러스(trus)는 정적으로 결정되는 것으로 설명된다.뉴턴의 법칙은 구조 전체뿐만 아니라 각 노드 또는 관절에도 적용됩니다.외부 부하 또는 힘에 노출될 수 있는 노드가 공간 내에서 정적인 상태를 유지하려면 모든(수평 및 수직) 힘의 합계와 노드 주위에 작용하는 모든 모멘트의 합계가 0이 되어야 합니다.각 노드에서 이러한 조건을 분석하면 압축력 또는 장력의 크기가 산출됩니다.
두 개 이상의 위치에서 지지되는 트러스들은 정적으로 불확정하다고 하며, 뉴턴의 법칙을 적용하는 것만으로는 부재력을 결정하는 데 충분하지 않다.
핀으로 연결된 부재를 가진 트러스가 안정되기 위해서는 완전히 [12]삼각형으로 구성될 필요가 없습니다.수학적 용어로 단순 트러스 안정성을 위해 다음과 같은 필요 조건이 있습니다.
여기서 m은 트러스 부재의 총수, j는 접합부의 총수, r은 2차원 구조에서의 반응수(일반적으로 3회)이다.
m - { m =일 때, 트러스의 외하중과 형상을 알게 되면 (m+3) 내부부재의 힘 및 지지반응이 2j 평형방정식으로 완전히 결정되기 때문에 트러스는 정적으로 결정된다고 한다.특정 수의 조인트가 지정되면 최소 멤버 수가 됩니다. 즉, 부재 중 하나가 제거(또는 고장)되면 트러스 전체가 고장납니다.(a)관계는 필요하지만 안정성에 있어서는 충분하지 않으며, 이는 트러스 형상, 지지조건 및 부재의 내하력에도 좌우된다.
일부 구조물은 최소 트러스 부재 수보다 더 많은 트러스 부재로 건설됩니다.그 구조들은 몇몇 구성원들이 실패하더라도 살아남을 수 있다.이들 부재의 힘은 기술된 평형 조건 외에 부재의 상대적 강성에 따라 달라진다.
분석.
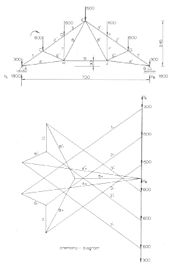
두 개의 주요 거더 각각에 가해지는 힘은 기본적으로 평면적이기 때문에 트러스도 보통 2차원 평면 프레임으로 모델링됩니다.그러나 상당한 평면 외 힘이 있는 경우, 구조물은 3차원 공간으로 모델링되어야 합니다.
트러스 해석에서는 종종 하중이 부재를 따라 중간점이 아닌 접합부에만 적용된다고 가정합니다.부재의 중량은 가해진 하중에 비해 경미하기 때문에 생략되는 경우가 많다.그렇지 않으면 각 부재의 중량의 절반이 2개의 엔드 조인트에 적용될 수 있다.부재가 길고 가늘면 조인트를 통해 전달되는 모멘트는 무시할 수 있으며 접합부는 "힌지" 또는 "핀 조인트"로 취급할 수 있다.
이러한 단순화된 가정 하에서 트러스의 모든 부재는 순수한 압축력 또는 순수한 장력을 받게 됩니다. 전단, 굽힘 모멘트 및 기타 복잡한 응력은 사실상 모두 0입니다.거의 모든 재료가 전단, 굽힘, 비틀림 또는 다른 종류의 힘보다 장력 또는 압축 시 훨씬 큰 하중을 견딜 수 있기 때문에 트러스는 구조 요소를 배열하는 다른 방법보다 물리적으로 강합니다.
이러한 단순화로 트러스 분석이 쉬워집니다.직접강성법, 플렉시블법, 유한요소법 등의 매트릭스법을 사용하여 어떤 종류의 트러스도 쉽게 구조해석을 할 수 있다.
구성원의 힘
그림은 9개의 조인트와 (2 x 9) - 3 = 15개의 멤버를 가진 단순하고 정적으로 결정된 플랫 트러스입니다.외부 하중은 외측 조인트에 집중됩니다.이것은 대칭적인 수직 하중을 가진 대칭 트러스이기 때문에 A와 B의 반력은 수직이고, 동일하며, 총 하중의 절반입니다.
트러스 부재의 내부 힘은 그래픽 방법을 포함하여 다양한 방법으로 계산할 수 있습니다.
부재 설계
트러스란 웹이 연속된 판이 아닌 일련의 개별 부재로 구성된 빔이라고 생각할 수 있습니다.트러스에서 하부 수평부재(하단현)와 상부 수평부재(상단현)는 장력 및 압축력을 가지며 I빔의 플랜지와 같은 기능을 한다.어떤 현이 장력을 전달하고 어떤 현이 압축을 전달하느냐는 전체적인 굽힘 방향에 따라 달라집니다.오른쪽의 트러스에서는 하현을 장력으로 하고 상현을 압축으로 하고 있습니다.
대각부재와 수직부재가 트러스웹을 형성하여 전단응력을 전달한다.또한 개별적으로 장력과 압축 상태에 있으며, 정확한 힘의 배열은 트러스 유형과 굽힘 방향에 따라 달라집니다.오른쪽 트러스에서는 수직부재가 장력상태이고 대각선이 압축상태이다.
부재는 정력을 운반하는 것 외에 서로 안정화시켜 좌굴을 방지하는 부가적인 기능을 한다.인접한 화상은 브레이싱의 존재와 웹 부재의 강성에 의해 상현 좌굴을 방지한다.
표시된 요소의 포함은 주로 경제성에 기초한 엔지니어링 결정이며, 이는 원자재 비용, 오프사이트 제작, 부품 운송, 현장 조립, 기계의 가용성 및 인건비 사이의 균형이다.다른 경우에는 구조물의 외관이 더 중요해지고, 따라서 단순한 경제 문제를 넘어 설계 결정에 영향을 미칠 수 있다.프리스트레스트 콘크리트와 같은 현대 재료와 자동 용접과 같은 제작 방법은 현대 교량 설계에 큰 영향을 미쳤다.
각 부재의 힘을 알면 다음 단계는 개별 트러스 부재의 단면을 결정하는 것입니다.장력을 받는 부재의 경우 단면적 A는 A = F × θ / θ를y 사용하여 구할 수 있다. 여기서 F는 부재의 힘이고, θ는 안전 계수(일반적으로 1.5이지만 건물 법규에 따라 다름)이고, θ는y 사용된 강철의 항복 인장 강도이다.
또한 압축 중인 부재는 좌굴로부터 안전하도록 설계되어야 한다.
트러스 부재의 중량은 단면에 직접 의존하며, 이 중량에 따라 트러스 내의 다른 부재의 강도가 부분적으로 결정됩니다.한 멤버에게 이전 반복보다 더 큰 단면을 부여하려면 다른 멤버에게도 더 큰 단면을 부여하여 첫 번째 멤버의 무게를 유지하도록 해야 합니다.다른 멤버의 필요량을 정확히 파악하려면 다른 반복을 수행해야 합니다.때때로 설계자는 설계 프로세스를 여러 번 반복하여 각 부재에 대해 "오른쪽" 단면에 수렴합니다.한편, 이전 반복에서 한 부재의 크기를 줄이면 다른 부재가 기술적으로 필요한 것보다 더 큰(그리고 더 비싼) 안전 계수를 갖게 될 뿐이지만, 제작 가능한 트러스를 찾기 위해 다른 반복 작업이 필요하지 않습니다.
교량 등 대형 트러스에서 개별 트러스 부재의 중량은 일반적으로 외부 하중의 힘에 비해 영향이 미미합니다.
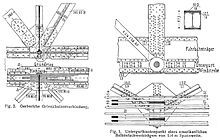
접합부 설계
부재의 최소 단면을 결정한 후 트러스 설계의 마지막 단계는 볼트 조인트의 상세(예: 조인트에 사용되는 볼트 연결부의 전단 응력 포함)가 될 것이다.프로젝트의 필요에 따라 트러스 내부 연결부(조인트)를 강성, 반강성 또는 힌지로 설계할 수 있습니다.견고한 연결은 벤딩 모멘트를 전달하여 부재의 2차 벤딩 모멘트를 발생시킬 수 있습니다.
적용들
포스트 프레임 구조
구성 요소 연결은 프레임 시스템의 구조적 무결성에 매우 중요합니다.크고 투명한 목재 트러스를 사용하는 건물에서 가장 중요한 연결부는 트러스와 지지대 사이의 연결부입니다.중력에 의한 힘(지지력 하중이라고도 함) 외에, 이러한 연결부는 트러스 평면에 수직으로 작용하는 전단력과 바람에 의한 상승력에 저항해야 한다.전체적인 건물 설계에 따라 벤딩 모멘트를 전달하기 위해 연결부가 필요할 수도 있습니다.
목재 기둥을 사용하면 대형 트러스와 벽 사이에 견고하고 직접적이지만 저렴한 연결을 만들 수 있습니다.포스트 투 트러스트 접속에 대한 자세한 내용은 설계자에 따라 다르며 포스트 타입에 따라 영향을 받을 수 있습니다.일반적으로 단단한 톱질 목재와 글램 기둥을 절단하여 트러스 지지면을 형성한다.트러스는 노치에 얹혀 제자리에 볼트로 고정된다.연결 부하 전달 능력을 높이기 위해 특수 플레이트/브래킷을 추가할 수 있습니다.기계적으로 적층된 기둥의 경우, 트러스는 단축된 외피 또는 단축된 내피 위에 놓일 수 있습니다.이후의 시나리오는 볼트를 이중 전단 상태로 하여 매우 효과적인 연결입니다.
갤러리
홍콩 중국은행 타워는 외부에서 볼 수 있는 트러스 구조를 가지고 있다
홍콩 HSBC 본관은 외부에서 볼 수 있는 트러스 구조를 가지고 있다.
1942년 북부 호주 전쟁부 소유물용으로 제작된 조립식 강철 활줄 지붕 트러스
프랑스 클루니 수도원의 옆 건물에 있는 지붕 트러스
퀸 포스트 목재 지붕 트러스를 통과하는 단면
「 」를 참조해 주세요.
- 격자탑
- Andreini 테셀레이션, 모든 곳에서 동일한 조인트를 가진 트러스 3D 공간을 채울 수 있는 유일한 28가지 방법
- 브라운 트러스
- 구 모양의 트러스인 지오데식 돔
- 구조역학
- Serrurier 트러스, 망원경에 사용되는 트러스 형태
- 스트레스:
- 구조용 강재
- Tensegrity 트러스, 압축 부재가 다른 압축 부재와 접촉하지 않는 트러스
- 트러스 로드, 기타 부품
레퍼런스
- ^ "Definition of TRUSS".
- ^ Plesha, Michael E.; Gray, Gary L.; Costanzo, Francesco (2013). Engineering Mechanics: Statics (2nd ed.). New York: McGraw-Hill Companies Inc. pp. 364–407. ISBN 978-0-07-338029-2.
- ^ 칭, 프랭크건축 비주얼 사전제2판호보켄, 뉴저지 주:와일리, 2012년, 277년, 인쇄물ISBN 97804706488
- ^ Bow R. H., 골조구조와 관련된 건설경제학.스폰, 런던, 1873년
- ^ Reif, F., etymonline.com (표준)
- ^ 옥스퍼드 영어사전
- ^ 노블, 앨런 조지전통적인 건축물은 구조 형태와 문화적 기능에 대한 세계적인 조사입니다.런던: I.B. 타우리스; 2007, 115.ISBN 1845113055
- ^ 데이비스, 니콜라, 그리고 에르키 조키니에미.건축 및 건축 공사 사전.암스테르담:Elsevier/Architecture Press, 2008. 394.ISBN 0750685026
- ^ 데이비스, 니콜라, 그리고 에르키 조키니에미.건축가의 일러스트 포켓 사전.옥스퍼드:Architectural Press, 2011. 121. ISBN 0080965377
- ^ 크랩, 조지유니버설 테크놀로지 사전 또는 모든 예술과 과학에서 사용되는 용어에 대한 친숙한 설명...," 제1권 런던: 1823.커플들.
- ^ 셰카르, R. K. 찬드라토목 공학 학술 사전.델리: Isha Books, 2005. 431. ISBN 8182051908
- ^ a b c Beer, Ferd; Johnston, Russ (2013). Vector Mechanics for Engineers: Statics (10th ed.). New York, NY: McGraw-Hill. pp. 285–313. ISBN 978-0-07-740228-0.
- ^ Ricker, Nathan Clifford (1912) [1912]. A Treat on Design and Construction of Roofs. New York: J. Wiley & Sons. p. 12. Retrieved 2008-08-15.
- ^ Maginnis, Owen Bernard (1903). Roof Framing Made Easy (2nd ed.). New York: The Industrial Publication Company. p. 9. Retrieved 2008-08-16.
- ^ a b c Hibbeler, Russell Charles (1983) [1974]. Engineering Mechanics-Statics (3rd ed.). New York: Macmillan Publishing Co., Inc. pp. 199–224. ISBN 0-02-354310-8.
- ^ Wingerter, R. 및 Labossiere, P., ME 354, Mechanics of Materials Laboratory: Structures, Washington 대학교 (2004년 2월), 페이지 1
- ^ Lubliner, Jacob; Papadopoulos, Panayiotis (2016-10-23). Introduction to Solid Mechanics: An Integrated Approach. Springer. ISBN 9783319188782.
- ^ Merriman, Mansfield (1912) [192]. American Civil Engineers' Pocket Book. New York: J. Wiley & Sons. p. 785. Retrieved 2008-08-16.
The Economic Depth of a Truss is that which makes the material in a bridge a minimum.
- ^ Bethanga Bridge 2011-06-09 NSW Heritage Office의 Wayback Machine에서 아카이브 완료, 2008-06년 2월 회수
- ^ 테네시 교통부의 테네시 주 피복 교량 개요, 2008년 2월 6일 취득
- ^ 2008-05-28 Maryland 교통부 제공으로 Wayback Machine에 보관된 Pratt Truss, 2008-2월 6일 회수
- ^ "1. Southern Pacific Railroad Bridge, Ash Avenue Bridge and Mill Avenue Bridge from Tempe Butte looking northwest. - Arizona Eastern Railroad Bridge, Spanning Salt River, Tempe, Maricopa County, AZ". Library of Congress. Retrieved 26 March 2020.
- ^ Tempe Historical Property Survey 2007-11-10년 Tempe Historical Museum 웨이백머신에서 아카이브된 Tempe Historical Property Survey 2008-2월 6일 취득
- ^ 케이스 웨스턴 리저브 대학의 다리오 가스파리니입니다라이트 형제와 프랫 트러스, 프레젠테이션 슬라이드
- ^ 2008년 5월 12일 웨이백 머신에 보관된 피복교 트러스 유형
- ^ 비에렌델 브루겐