파라콤팩트 균일 벌집

파라콤팩트 일반 허니컴의 예

{3,3,6}	{6,3,3}	{4,3,6}	{6,3,4}
{5,3,6}	{6,3,5}	{6,3,6}	{3,6,3}
{4,4,3}	{3,4,4}	{4,4,4}

기하학에서 쌍곡선 공간의 균일한 벌집들은 볼록한 균일한 다면세포의 테셀레이션이다.3차원 쌍곡선 공간에는 위트오프 구조로 생성되고 각 패밀리의 Coxeter 다이어그램의 링 순열로 표현되는 파라콤팩트 균일한 벌집형 23개 그룹 패밀리가 있다.이러한 패밀리는 무한의 이상적인 정점을 포함하여 무한하거나 한이 없는 면이나 정점 형상을 가진 균일한 벌집을 만들 수 있으며, 2차원 쌍곡선 기울기와 유사하다.

일반 파라콤팩트 벌집

균일한 파라콤팩트 H³ 허니콤 중 11개는 규칙적인 것으로, 그들의 대칭 집단이 그들의 깃발에서 전이적으로 작용한다는 것을 의미한다.이들은 Schléfli 기호 {3,3,6}, {6,3,3}, {3,4,4,4}, {4,3}, {3,6,3}, {4,3,6}, {4,4,4}, {5,3,6}, {6,3,5}, {6},6}을 가지며, 아래에 나와 있다.4개의 유한 이상 다면세포가 있다: {3,3,6}, {4,3,6}, {3,4,4}, {5,3,6}.

11개의 파라콤팩트 일반 꿀벌집
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

이름	슐레플리 기호 {p,q,r}	콕시터	셀 타자를 치다 {p,q}	면 타자를 치다 {p}	가장자리 형상을 나타내다 {r}	꼭지점 형상을 나타내다 {q,r}	이중	콕시터 무리를 짓다
순서 6 사면 벌집	{3,3,6}		{3,3}	{3}	{6}	{3,6}	{6,3,3}	[6,3,3]
육각 타일링 벌집	{6,3,3}		{6,3}	{6}	{3}	{3,3}	{3,3,6}
순서-4 팔면 벌집	{3,4,4}		{3,4}	{3}	{4}	{4,4}	{4,4,3}	[4,4,3]
사각 타일링 벌집	{4,4,3}		{4,4}	{4}	{3}	{4,3}	{3,4,4}
삼각 타일링 벌집	{3,6,3}		{3,6}	{3}	{3}	{6,3}	셀프듀얼	[3,6,3]
오더-6입방 벌집	{4,3,6}		{4,3}	{4}	{4}	{3,6}	{6,3,4}	[6,3,4]
순서-4 육각형 타일링 벌집	{6,3,4}		{6,3}	{6}	{4}	{3,4}	{4,3,6}
순서-4 사각 타일링 벌집	{4,4,4}		{4,4}	{4}	{4}	{4,4}	셀프듀얼	[4,4,4]
주문-6도면체 벌집	{5,3,6}		{5,3}	{5}	{5}	{3,6}	{6,3,5}	[6,3,5]
순서-5 육각 타일링 벌집	{6,3,5}		{6,3}	{6}	{5}	{3,5}	{5,3,6}
오더-6 육각형 타일링 벌집	{6,3,6}		{6,3}	{6}	{6}	{3,6}	셀프듀얼	[6,3,6]

파라콤팩트 균일한 벌집합들의 콕시터 그룹

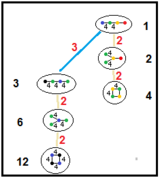이 그래프들은 파라콤팩트 쌍곡선 Coxeter 그룹의 부분군 관계를 보여준다.순서 2 부분군은 거울 대칭의 평면으로 구르사트 사면체를 이등분하는 것을 나타낸다.

이것은 사면체 기본 영역(순위 4개 파라콤팩트 콕시터 그룹)에서 생성된 151개의 고유한 와이토피아 파라콤팩트 균일 벌집을 완전히 열거한 것이다.꿀콤은 이중 양식을 상호 참조하기 위해 여기서 색인화되며, 비주요 건축물을 중심으로 괄호가 있다.

교체가 나열되지만 반복되거나 균일한 솔루션을 생성하지 않는다.단일 홀 교체는 미러 탈거 작업을 의미한다.엔드 노드가 제거되면 또 다른 심플렉스(테트라헤드) 패밀리가 생성된다.구멍에 두 개의 분기가 있으면 빈버그 폴리토프(Vinberg polytope)가 생성되는데, 거울 대칭이 있는 빈버그 폴리토프만이 심플렉스 그룹과 관련이 있고, 이들의 균일한 허니콤은 체계적으로 탐구되지 않았다.4면체 그룹의 반쪽 그룹에 대한 특별한 경우를 제외하고, 이러한 비강제(피강) Coxeter 그룹은 이 페이지에 열거되지 않는다.

사면 쌍곡선 포물선 그룹 요약

콕시터군		심플렉스 부피	정류자 부분군	고유 벌집 수
[6,3,3]		0.0422892336	[1+,6,(3,3)+] = [3,3[3]]+	15
[4,4,3]		0.0763304662	[1+,4,1+,4,3+]	15
[3,3[3]]		0.0845784672	[3,3[3]]+	4
[6,3,4]		0.1057230840	[1+,6,3+,4,1+] = [3[]x[]]+	15
[3,41,1]		0.1526609324	[3+,41+,1+]	4
[3,6,3]		0.1691569344	[3+,6,3+]	8
[6,3,5]		0.1715016613	[1+,6,(3,5)+] = [5,3[3]]+	15
[6,31,1]		0.2114461680	[1+,6,(31,1)+] = [3[]x[]]+	4
[4,3[3]]		0.2114461680	[1+,4,3[3]]+ = [3[]x[]]+	4
[4,4,4]		0.2289913985	[4+,4+,4+]+	6
[6,3,6]		0.2537354016	[1+,6,3+,6,1+] = [3[3,3]]+	8
[(4,4,3,3)]		0.3053218647	[(4,1+,4,(3,3)+)]	4
[5,3[3]]		0.3430033226	[5,3[3]]+	4
[(6,3,3,3)]		0.3641071004	[(6,3,3,3)]+	9
[3[]x[]]		0.4228923360	[3[]x[]]+	1
[41,1,1]		0.4579827971	[1+,41+,1+,1+]	0
[6,3[3]]		0.5074708032	[1+,6,3[3]] = [3[3,3]]+	2
[(6,3,4,3)]		0.5258402692	[(6,3+,4,3+)]	9
[(4,4,4,3)]		0.5562821156	[(4,1+,4,1+,4,3+)]	9
[(6,3,5,3)]		0.6729858045	[(6,3,5,3)]+	9
[(6,3,6,3)]		0.8457846720	[(6,3+,6,3+)]	5
[(4,4,4,4)]		0.9159655942	[(4+,4+,4+,4+)]	1
[3[3,3]]		1.014916064	[3[3,3]]+	0

비강제적(비강제적) 파라콤팩트 Coxeter 그룹의 전체 목록은 P에 의해 발표되었다.2003년 투마르킨.^[1]H에서³ 가장 작은 파라콤팩트 형태는 , 또는 [3,3,3,3,3,3]으로 나타낼 수 있는데, 파라콤팩트 쌍곡선 그룹[3,4]을 [3,4⁺]로 거울 제거하여 구성할 수 있다. 2중 기본 영역이 사면체에서 사면체 피라미드로 바뀐다.또 다른 피라미드는 또는 [4,4,1⁺,4] = [4,4,4,4,4,4] : = .

Removing a mirror from some of the cyclic hyperbolic Coxeter graphs become bow-tie graphs: [(3,3,4,1⁺,4)] = [((3,∞,3)),((3,∞,3))] or , [(3,4,4,1⁺,4)] = [((4,∞,3)),((3,∞,4))] or , [(4,4,4,1⁺,4)] = [((4,∞,4)),((4,∞,4))] or . = , = , = .

또 다른 과소평가된 반쪽 그룹은 파운드다.

급진적인 비선택적 부분군은 파운드로, 이것은 파운드로 삼각형 프리즘 영역으로 두 배가 될 수 있다.

피라미드 쌍곡선 포물선 그룹 요약

치수	순위	그래프
H3	5

선형 그래프

[6,3,3]가족

#	벌집 이름 Coxeter 다이어그램: 슐레플리 기호	위치별 셀 (각 꼭지점 주위로 카운트)				정점수	사진
		1	2	3	4
1	육각형의 {6,3,3}	-	-	-	(4) (6.6.6)	사면체
2	정류된 육각형 t1{6,3,3} 또는 r{6,3,3}	(2) (3.3.3)	-	-	(3) (3.6.3.6)	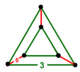삼각 프리즘
3	수정 순서-6 사면체 t1{3,3,6} 또는 r{3,3,6}	(6) (3.3.3.3)	-	-	(2) (3.3.3.3.3.3)	육각 프리즘
4	order-6 사면체 {3,3,6}	(∞) (3.3.3)	-	-	-	삼각 타일링
5	잘린 육각형 t0,1{6,3,3} 또는 t{6,3,3}	(1) (3.3.3)	-	-	(3) (3.12.12)	삼각피라미드
6	통조림 t0,2{6,3,3} 또는 rr{6,3,3}	(1) 3.3.3.3	(2) (4.4.3)	-	(2) (3.4.6.4)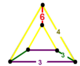
7	육각형의 달팽이관 t0,3{6,3,3}	(1) (3.3.3)	(3) (4.4.3)	(3) (4.4.6)	(1) (6.6.6)
8	알 수 있는 명령-6 사면체 t0,2{3,3,6} 또는 rr{3,3,6}	(1) (3.4.3.4)	-	(2) (4.4.6)	(2) (3.6.3.6)
9	굵게 깎은 육각형 t1,2{6,3,3} 또는 2t{6,3,3}	(2) (3.6.6)	-	-	(2) (6.6.6)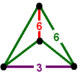
10	잘린서-6 사면체 t0,1{3,6} 또는 t{3,3,6}	(6) (3.6.6)	-	-	(1) (3.3.3.3.3.3)
11	캔트런으로 된 육각형 t0,1,2{6,3,3} 또는 tr{6,3,3}	(1) (3.6.6)	(1) (4.4.3)	-	(2) (4.6.12)
12	구불구불한 육각형 t0,1,3{6,3,3}	(1) (3.4.3.4)	(2) (4.4.3)	(1) (4.4.12)	(1) (3.12.12)
13	6 사면구획 t0,1,3{3,3,6}	(1) (3.6.6)	(1) (4.4.6)	(2) (4.4.6)	(1) (3.4.6.4)
14	캔트런 경도 순서-6 사면체 t0,1,2{3,3,6} 또는 tr{3,3,6}	(2) (4.6.6)	-	(1) (4.4.6)	(1) (6.6.6)
15	의 육각형. t0,1,2,3{6,3,3}	(1) (4.6.6)	(1) (4.4.6)	(1) (4.4.12)	(1) (4.6.12)

대식식

#	이름 이름 Coxeter 다이어그램: 슐레플리 기호	셀 (각 꼭지점 주위로 카운트)						사
		1	2	3	4	알트
[137]	( ↔ ) =	-	-		(4) (3.3.3.3.3.3)	(4) (3.3.3)	(3.6.6)
[138]	통조림 육각형 ↔	(1) (3.3.3.3)	-		(2) (3.6.3.6)	(2) (3.6.6)
[139]	↔	(1) (4.4.4)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.3.4)
[140]	대서방 육각형 ↔	(1) (3.6.6)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.6)
일일요	스너브 수정 순서-6 사면체 ↔ sr{3,6} sr{3,6}					관개(3.3.3)
일일요	광합성 스너브 순서-6 사면체 sr3{3,6}
일일요	옴니즈너브 순서-6 사면체 ht0,1,2,3{6,3,3}					관개(3.3.3)

[6,3,4]가족

Coxeter 그룹의 링 순열에 의해 생성되는 15가지 형태가 있다. [6,3,4] 또는

#	콕시터 다이어그램 슐레플리 기호	꼭지점당 위치 및 카운트별 셀					사
		0	1	2	3
16	(정규) 순서-4 육각형 {6,3,4}	-	-	-	(8) (6.6.6)	(3.3.3.3)
17	순서-4 육각형 t1{6,3,4} 또는 r{6,3,4}	(2) (3.3.3.3)	-	-	(4) (3.6.3.6)	(4.4.4)
18	수정 순서-6입방체 t1{4,3,6} 또는 r{4,3,6}	(6) (3.4.3.4)	-	-	(2) (3.3.3.3.3.3)	(6.4.4)
19	오더-6 입방체 {4,3,6}	(20) (4.4.4)	-	-	-	(3.3.3.3.3.3)
20	순서-4 육각형 t0,1{6,3,4} 또는 t{6,3,4}	(1) (3.3.3.3)	-	-	(4) (3.12.12)
21	잘린 순서-6 입방체 t1,2{6,3,4} 또는 2t{6,3,4}	(2) (4.6.6)	-	-	(2) (6.6.6)
22	잘린 순서-6 입방체 t0,1{4,3,6} 또는 t{4,3,6}	(6) (3.8.8)	-	-	(1) (3.3.3.3.3.3)
23	알 수 있는 순서-4 육각형 t0,2{6,3,4} 또는 rr{6,3,4}	(1) (3.4.3.4)	(2) (4.4.4)	-	(2) (3.4.6.4)
24	알 수 있는 주문-6 입방체 t0,2{4,3,6} 또는 rr{4,3,6}	(2) (3.4.4.4)	-	(2) (4.4.6)	(1) (3.6.3.6)
25	런케이트 오더-6 입방체 t0,3{6,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.6)	(1) (6.6.6)
26	순서-4 육각형 t0,1,2{6,3,4} 또는 tr{6,3,4}	(1) (4.6.6)	(1) (4.4.4)	-	(2) (4.6.12)
27	캔트런치 오더-6 입방체 t0,1,2{4,3,6} 또는 tr{4,3,6}	(2) (4.6.8)	-	(1) (4.4.6)	(1) (6.6.6)
28	런커런티드 오더-4 육각형 t0,1,3{6,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.12)	(1) (3.12.12)
29	6인치 t0,1,3{4,3,6}	(1) (3.8.8)	(2) (4.4.8)	(1) (4.4.6)	(1) (3.4.6.4)
30	전분산 오더-6 입방체 t0,1,2,3{6,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.12)	(1) (4.6.12)

대식식

#	콕시터 다이어그램 슐레플리 기호	꼭지점당 위치 및 카운트별 셀						사
		0	1	2	3	알트
[87]	교번 오더-6 입방체 ↔ h{4,3,6}	(3.3.3)				(3.3.3.3.3.3)	(3.6.3.6)
[88]	캔틱 오더-6 입방체 ↔ h2{4,3,6}	(2) (3.6.6)	-	-	(1) (3.6.3.6)	(2) (6.6.6)
[89]	런치 오더-6 입방체 ↔ h3{4,3,6}	(1) (3.3.3)	-	-	(1) (6.6.6)	(3) (3.4.6.4)
[90]	런시코틱 오더-6 입방체 ↔ h2,3{4,3,6}	(1) (3.6.6)	-	-	(1) (3.12.12)	(2) (4.6.12)
[141]	순서-4 육각형 ↔ ↔ h{6,3,4}	-	-		(3.3.3.3.3.3)	(3.3.3.3)	(4.6.6)
[142]	↔ ↔ h1{6,3,4}	(1) (3.4.3.4)	-		(2) (3.6.3.6)	(2) (4.6.6)
[143]	런치 순서-4 육각형 ↔ h3{6,3,4}	(1) (4.4.4)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.4.4)
[144]	런코코틱 순서-4 육각형 ↔ h2,3{6,3,4}	(1) (3.8.8)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.8)
[151]	4분의 1 순서-4 육각형 ↔ q{6,3,4}	(3)	(1)	-	(1)	(3)
일일요	비스눕 순서-6 입방체 ↔ 2s{4,3,6}	(3.3.3.3.3.3)	-	-	(3.3.3.3.6)	+(3.3.3)
일일요	런치 비스눕 순서-6 입방체
일일요	스너브 정류 순서 6입방체 ↔ sr{4,3,6}	(3.3.3.3.3)	(3.3.3)	(3.3.3.4)	(3.3.3.3.6)	+(3.3.3)
일일요	6입방런cic snub 수리가능서-6입방체 sr3{4,3,6}
일일요	스너브 정류 순서-4 육각형 ↔ sr{6,3,4}	(3.3.3.3.3.3)	(3.3.3)	-	(3.3.3.3.6)	+(3.3.3)
일일요	런시니럽 정류 순서-4 육각형 sr3{6,3,4}
일일요	수정 주문서 6입방 입방체 ht0,1,2,3{6,3,4}	(3.3.3.3.4)	(3.3.3.4)	(3.3.3.6)	(3.3.3.3.6)	+(3.3.3)

[6,3,5]가족

#	이름 이름 콕시터 다이어그램 슐레플리 기호	셀 (각 꼭지점 주위로 카운트)					사
		0	1	2	3
31	육각형 {6,3,5}	-	-	-	(20) (6)3	이코사헤드론
32	수정이능정 육각형서-5 육각형 t1{6,3,5} 또는 r{6,3,5}	(2) (3.3.3.3.3)	-	-	(5) (3.6)2	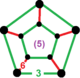(5.4.4)
33	t1{5,3,6} 또는 r{5,3,6}	(5) (3.5.3.5)	-	-	(2) (3)6	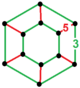(6.4.4)
34	도라면면 {5,3,6}	(5.5.5)	-	-	-	(∞) (3)6
35	순서-5 육각형 t0,1{6,3,5} 또는 t{6,3,5}	(1) (3.3.3.3.3)	-	-	(5) 3.12.12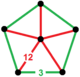
36	알 수 있는 순서-5 육각형 t0,2{6,3,5} 또는 rr{6,3,5}	(1) (3.5.3.5)	(2) (5.4.4)	-	(2) 3.4.6.4
37	도도면 t0,3{6,3,5}	(1) (5.5.5)	-	(6) (6.4.4)	(1) (6)3
38	수 있는 6 도도면 t0,2{5,3,6} 또는 rr{5,3,6}	(2) (4.3.4.5)	-	(2) (6.4.4)	(1) (3.6)2
39	순서-6 도도면 t1,2{6,3,5} 또는 2t{6,3,5}	(2) (5.6.6)	-	-	(2) (6)3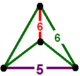
40	t0,1{5,3,6} 또는 t{5,3,6}	(6) (3.10.10)	-	-	(1) (3)6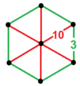
41	오더-5 육각형 t0,1,2{6,3,5} 또는 tr{6,3,5}	(1) (5.6.6)	(1) (5.4.4)	-	(2) 4.6.10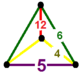
42	런커런티드 오더-5 육각형 t0,1,3{6,3,5}	(1) (4.3.4.5)	(1) (5.4.4)	(2) (12.4.4)	(1) 3.12.12
43	리리 6 도도면 t0,1,3{5,3,6}	(1) (3.10.10)	(1) (10.4.4)	(2) (6.4.4)	(1) 3.4.6.4
44	캔트런으로 갈린 순서-6 도데카헤드랄 t0,1,2{5,3,6} 또는 tr{5,3,6}	(1) (4.6.10)	-	(2) (6.4.4)	(1) (6)3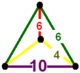
45	도 6도면도 t0,1,2,3{6,3,5}	(1) (4.6.10)	(1) (10.4.4)	(1) (12.4.4)	(1) 4.6.12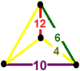

대식식

#	이름 이름 콕시터 다이어그램 슐레플리 기호	셀 (각 꼭지점 주위로 카운트)						사
		0	1	2	3	알트
[145]	순서-5 육각형 ↔ h{6,3,5}	-	-	-	(20) (3)6	(12) (3)5	(5.6.6)
[146]	캔틱 순서-5 육각형 ↔ h2{6,3,5}	(1) (3.5.3.5)	-		(2) (3.6.3.6)	(2) (5.6.6)
[147]	런치 오더-5 육각형 ↔ h3{6,3,5}	(1) (5.5.5)	(1) (4.4.3)		(1) (3.3.3.3.3.3)	(3) (3.4.5.4)
[148]	런코코틱 오더-5 육각형 ↔ h2,3{6,3,5}	(1) (3.10.10)	(1) (4.4.3)		(1) (3.6.3.6)	(2) (4.6.10)
일일요	스너브 수정 순서-6 도치형 ↔ sr{5,3,6}	(3.3.5.3.5)	-	(3.3.3.3)	(3.3.3.3.3.3)	관개하다
일일요	옴니스너브 순서-5 육각형 ht0,1,2,3{6,3,5}	(3.3.5.3.5)	(3.3.3.5)	(3.3.3.6)	(3.3.6.3.6)	관개하다

[6,3,6]가족

Coxeter 그룹의 링 순열에 의해 생성되는 9가지 형태가 있다. [6,3,6] 또는

#	콕시터 다이어그램 슐레플리 기호	꼭지점당 위치 및 카운트별 셀					사
		0	1	2	3
46	오더-6 육각형 {6,3,6}	-	-	-	(20) (6.6.6)	(3.3.3.3.3.3)
47	정류서-6 육각형 t1{6,3,6} 또는 r{6,3,6}	(2) (3.3.3.3.3.3)	-	-	(6) (3.6.3.6)	(6.4.4)
48	순서-6 육각형 t0,1{6,3,6} 또는 t{6,3,6}	(1) (3.3.3.3.3.3)	-	-	(6) (3.12.12)
49	알 수 있는 순서-6 육각형 t0,2{6,3,6} 또는 rr{6,3,6}	(1) (3.6.3.6)	(2) (4.4.6)	-	(2) (3.6.4.6)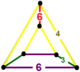
50	런케이티드 오더-6 육각형 t0,3{6,3,6}	(1) (6.6.6)	(3) (4.4.6)	(3) (4.4.6)	(1) (6.6.6)
51	오더-6 육각형 t0,1,2{6,3,6} 또는 tr{6,3,6}	(1) (6.6.6)	(1) (4.4.6)	-	(2) (4.6.12)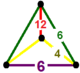
52	런커런티드 오더-6 육각형 t0,1,3{6,3,6}	(1) (3.6.4.6)	(1) (4.4.6)	(2) (4.4.12)	(1) (3.12.12)
53	순서-6 육각형 t0,1,2,3{6,3,6}	(1) (4.6.12)	(1) (4.4.12)	(1) (4.4.12)	(1) (4.6.12)
[1]	육각bitrunculated order-6 육각형 ↔ ↔ t1,2{6,3,6} 또는 2t{6,3,6}	(2) (6.6.6)	-	-	(2) (6.6.6)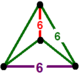

대식식

#	콕시터 다이어그램 슐레플리 기호	꼭지점당 위치 및 카운트별 셀						사
		0	1	2	3	알트
[47]	정류서-6 육각형 ↔ ↔ q{6,3,6} = r{6,3,6}	(2) (3.3.3.3.3.3)	-	-	(6) (3.6.3.6)		(6.4.4)
[54]	삼각형의 ( ↔ ) = h{6,3} = {3,6,3}	-	-	-	(3.3.3.3.3.3)	(3.3.3.3.3.3)	{6,3}
[55]	캔틱 순서-6 육각형 ( ↔ ) = h2{6,3,6} = r{3,6,3}	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)
[149]	런치 오더-6 육각형 ↔ h3{6,3,6}	(1) (6.6.6)	(1) (4.4.3)	(3) (3.4.6.4)	(1) (3.3.3.3.3.3)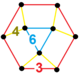
[150]	런코코틱 오더-6 육각형 ↔ h2,3{6,3,6}	(1) (3.12.12)	(1) (4.4.3)	(2) (4.6.12)	(1) (3.6.3.6)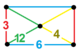
[137]	( ↔ ↔ ) = = 2s{6,3,6} = h{6,3}	(3.3.3.3.6)	-	-	(3.3.3.3.6)	+(3.3.3)	(3.6.6)
일일요	스너브 정류 순서-6 육각형 sr{6,3,6}	(3.3.3.3.3.3)	(3.3.3.3)	-	(3.3.3.3.6)	+(3.3.3)
일일요	런케인드 오더-6 육각형 ht0,3{6,3,6}	(3.3.3.3.3.3)	(3.3.3.3)	(3.3.3.3)	(3.3.3.3.3.3)	+(3.3.3)
일일요	옴니스너브 순서-6 육각형 ht0,1,2,3{6,3,6}	(3.3.3.3.6)	(3.3.3.6)	(3.3.3.6)	(3.3.3.3.6)	+(3.3.3)

[3,6,3]가족

Coxeter 그룹의 링 순열에 의해 생성되는 9가지 형태가 있다. [3,6,3] 또는

#	이름 이름 콕시터 다이어그램 슐래플리 기호	셀 카운트/버텍스 그리고 벌집 안의 위치들					사
		0	1	2	3
54	삼각형의 {3,6,3}	-	-	-	(∞) {3,6}	{6,3}
55	된 삼각형 t1{3,6,3} 또는 r{3,6,3}	(2) (6)3	-	-	(3) (3.6)2	(3.4.4)
56	세모꼴로 알 수 있는 t0,2{3,6,3} 또는 rr{3,6,3}	(1) (3.6)2	(2) (4.4.3)	-	(2) (3.6.4.6)
57	삼각으로 장식한 삼각형 t0,3{3,6,3}	(1) (3)6	(6) (4.4.3)	(6) (4.4.3)	(1) (3)6
58	세모꼴로 갈라진 t1,2{3,6,3} 또는 2t{3,6,3}	(2) (3.12.12)	-	-	(2) (3.12.12)
59	세모꼴로 된 칸트런 t0,1,2{3,6,3} 또는 tr{3,6,3}	(1) (3.12.12)	(1) (4.4.3)	-	(2) (4.6.12)
60	삼각형으로 늘어뜨린 t0,1,3{3,6,3}	(1) (3.6.4.6)	(1) (4.4.3)	(2) (4.4.6)	(1) (6)3
61	삼각형 t0,1,2,3{3,6,3}	(1) (4.6.12)	(1) (4.4.6)	(1) (4.4.6)	(1) (4.6.12)
[1]	삼각형 ↔ ↔ t0,1{3,6,3} 또는 t{3,6,3} = {6,3,3}	(1) (6)3	-	-	(3) (6)3	{3,3}

대식식

#	이름 이름 콕시터 다이어그램 슐래플리 기호	셀 카운트/버텍스 그리고 벌집 안의 위치들						사
		0	1	2	3	알트
[56]	세모꼴로 알 수 있는 = s2{3,6,3}	(1) (3.6)2	-	-	(2) (3.6.4.6)	(3.4.4)
[60]	삼각형으로 늘어뜨린 = s2,3{3,6,3}	(1) (6)3	-	(1) (4.4.3)	(1) (3.6.4.6)	(2) (4.4.6)
[137]	( ↔ ) = ( ↔ ) s{3,6,3}	(3)6	-	-	(3)6	+(3)3	(3.6.6)
스칼리폼	삼각형 모양의 런시스너브 s3{3,6,3}	r{6,3}	-	(3.4.4)	(3)6	트라이크업
통일형	삼각 타일링 벌집 ht0,1,2,3{3,6,3}	(3.3.3.3.6)	(3)4	(3)4	(3.3.3.3.6)	+(3)3

[4,4,3]가족

Coxeter 그룹의 링 순열에 의해 생성되는 15가지 형태가 있다: [4,4,3] 또는

#	벌집 이름 콕시터 다이어그램 슐래플리 기호	셀 카운트/버텍스 그리고 벌집 안의 위치들				정점수	사진
		0	1	2	3
62	정사각형의 = {4,4,3}	-	-	-	(6)	큐브
63	정사각형 = t1{4,4,3} 또는 r{4,4,3}	(2)	-	-	(3)	삼각 프리즘
64	수정 순서-4 팔면체 t1{3,4,4} 또는 r{3,4,4}	(4)	-	-	(2)
65	order-4 팔면체 {3,4,4}	(∞)	-	-	-
66	잘린 사각형 = t0,1{4,4,3} or t{4,4,3}	(1)	-	-	(3)
67	truncated order-4 octahedral t0,1{3,4,4} or t{3,4,4}	(4)	-	-	(1)
68	bitruncated square t1,2{4,4,3} or 2t{4,4,3}	(2)	-	-	(2)
69	cantellated square t0,2{4,4,3} or rr{4,4,3}	(1)	(2)	-	(2)
70	cantellated order-4 octahedral t0,2{3,4,4} or rr{3,4,4}	(2)	-	(2)	(1)
71	runcinated square t0,3{4,4,3}	(1)	(3)	(3)	(1)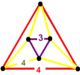
72	cantitruncated square t0,1,2{4,4,3} or tr{4,4,3}	(1)	(1)	-	(2)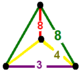
73	cantitruncated order-4 octahedral t0,1,2{3,4,4} or tr{3,4,4}	(2)	-	(1)	(1)
74	runcitruncated square t0,1,3{4,4,3}	(1)	(1)	(2)	(1)
75	runcitruncated order-4 octahedral t0,1,3{3,4,4}	(1)	(2)	(1)	(1)
76	omnitruncated square t0,1,2,3{4,4,3}	(1)	(1)	(1)	(1)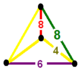

Alternated forms

#	Honeycomb name Coxeter diagram and Schläfli symbol	Cell counts/vertex and positions in honeycomb					Vertex figure	Picture
		0	1	2	3	Alt
[83]	alternated square ↔ h{4,4,3}	-	-	-		{4,3}	(4.3.4.3)
[84]	cantic square ↔ h2{4,4,3}	(3.4.3.4)	-	(3.8.8)		(4.8.8)
[85]	runcic square ↔ h3{4,4,3}	(3.3.3.3)	-	(3.4.4.4)		(4.4.4)
[86]	runcicantic square ↔	(4.6.6)	-	(3.4.4.4)		(4.8.8)
Nonsimplectic	alternated rectified square ↔ hr{4,4,3}		-	-		{}x{3}
Scaliform	snub order-4 octahedral = = s{3,4,4}		-	-		{}v{4}
Scaliform	runcisnub order-4 octahedral s3{3,4,4}					cup-4
152	snub square = s{4,4,3}		-	-		{3,3}
Nonuniform	snub rectified order-4 octahedral sr{3,4,4}		-			irr. {3,3}
Nonuniform	alternated runcitruncated square ht0,1,3{3,4,4}					irr. {}v{4}
Nonuniform	omnisnub square ht0,1,2,3{4,4,3}					irr. {3,3}

[4,4,4] family

There are 9 forms, generated by ring permutations of the Coxeter group: [4,4,4] or .

#	Honeycomb name Coxeter diagram and Schläfli symbol	Cell counts/vertex and positions in honeycomb				Symmetry	Vertex figure	Picture
		0	1	2	3
77	order-4 square {4,4,4}	-	-	-		[4,4,4]	Cube
78	truncated order-4 square t0,1{4,4,4} or t{4,4,4}		-	-		[4,4,4]
79	bitruncated order-4 square t1,2{4,4,4} or 2t{4,4,4}		-	-		[[4,4,4]]
80	runcinated order-4 square t0,3{4,4,4}					[[4,4,4]]
81	runcitruncated order-4 square t0,1,3{4,4,4}					[4,4,4]
82	omnitruncated order-4 square t0,1,2,3{4,4,4}					[[4,4,4]]
[62]	square ↔ t1{4,4,4} or r{4,4,4}		-	-		[4,4,4]	Square tiling
[63]	rectified square ↔ t0,2{4,4,4} or rr{4,4,4}			-		[4,4,4]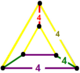
[66]	truncated order-4 square ↔ t0,1,2{4,4,4} or tr{4,4,4}			-		[4,4,4]

Alternated constructions

#	Honeycomb name Coxeter diagram and Schläfli symbol	Cell counts/vertex and positions in honeycomb					Symmetry	Vertex figure	Picture
		0	1	2	3	Alt
[62]	Square ( ↔ ↔ ↔ ) =	(4.4.4.4)	-	-		(4.4.4.4)	[1+,4,4,4] =[4,4,4]
[63]	rectified square = s2{4,4,4}			-			[4+,4,4]
[77]	order-4 square ↔ ↔ ↔	-	-	-			[1+,4,4,4] =[4,4,4]	Cube
[78]	truncated order-4 square ↔ ↔ ↔	(4.8.8)	-	(4.8.8)	-	(4.4.4.4)	[1+,4,4,4] =[4,4,4]
[79]	bitruncated order-4 square ↔ ↔ ↔	(4.8.8)	-	-	(4.8.8)	(4.8.8)	[1+,4,4,4] =[4,4,4]
[81]	runcitruncated order-4 square tiling = s2,3{4,4,4}						[4,4,4]
[83]	alternated square ( ↔ ) ↔ hr{4,4,4}		-	-			[4,1+,4,4]	(4.3.4.3)
[104]	quarter order-4 square ↔ q{4,4,4}						[[1+,4,4,4,1+]] =[[4[4]]]
153	alternated rectified square tiling ↔ ↔ hrr{4,4,4}			-			[((2+,4,4)),4]
154	alternated runcinated order-4 square tiling ht0,3{4,4,4}						[[(4,4,4,2+)]]
Scaliform	snub order-4 square tiling s{4,4,4}		-	-			[4+,4,4]
Nonuniform	runcic snub order-4 square tiling s3{4,4,4}						[4+,4,4]
Nonuniform	bisnub order-4 square tiling 2s{4,4,4}		-	-			[[4,4+,4]]
[152]	snub square tiling ↔ sr{4,4,4}			-			[(4,4)+,4]
Nonuniform	alternated runcitruncated order-4 square tiling ht0,1,3{4,4,4}						[((2,4)+,4,4)]
Nonuniform	omnisnub order-4 square tiling ht0,1,2,3{4,4,4}						[[4,4,4]]+

Tridental graphs

[3,4^1,1] family

There are 11 forms (of which only 4 are not shared with the [4,4,3] family), generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	0'	3
83	alternated square ↔	-	-	(4.4.4)	(4.4.4.4)	(4.3.4.3)
84	cantic square ↔	(3.4.3.4)	-	(3.8.8)	(4.8.8)
85	runcic square ↔	(4.4.4.4)	-	(3.4.4.4)	(4.4.4.4)
86	runcicantic square ↔	(4.6.6)	-	(3.4.4.4)	(4.8.8)
[63]	rectified square ↔	(4.4.4)	-	(4.4.4)	(4.4.4.4)
[64]	rectified order-4 octahedral ↔	(3.4.3.4)	-	(3.4.3.4)	(4.4.4.4)
[65]	order-4 octahedral ↔	(4.4.4.4)	-	(4.4.4.4)	-
[67]	truncated order-4 octahedral ↔	(4.6.6)	-	(4.6.6)	(4.4.4.4)
[68]	bitruncated square ↔	(3.8.8)	-	(3.8.8)	(4.8.8)
[70]	cantellated order-4 octahedral ↔	(3.4.4.4)	(4.4.4)	(3.4.4.4)	(4.4.4.4)
[73]	cantitruncated order-4 octahedral ↔	(4.6.8)	(4.4.4)	(4.6.8)	(4.8.8)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	0'	3	Alt
Scaliform	snub order-4 octahedral = = s{3,41,1}		-	-		irr. {}v{4}
Nonuniform	snub rectified order-4 octahedral ↔ sr{3,41,1}	(3.3.3.3.4)	(3.3.3)	(3.3.3.3.4)	(3.3.4.3.4)	+(3.3.3)

[4,4^1,1] family

There are 7 forms, (all shared with [4,4,4] family), generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter diagram	Cells by location				Vertex figure	Picture
		0	1	0'	3
[62]	Square ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)
[62]	Square ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)
[63]	rectified square ( ↔ ) =	(4.4.4.4)	(4.4.4)	(4.4.4.4)	(4.4.4.4)
[66]	truncated square ( ↔ ) =	(4.8.8)	(4.4.4)	(4.8.8)	(4.8.8)
[77]	order-4 square ↔	(4.4.4.4)	-	(4.4.4.4)	-
[78]	truncated order-4 square ↔	(4.8.8)	-	(4.8.8)	(4.4.4.4)
[79]	bitruncated order-4 square ↔	(4.8.8)	-	(4.8.8)	(4.8.8)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	0'	3	Alt
[77]	order-4 square ( ↔ ↔ ) =		-		-	Cube
[78]	truncated order-4 square ( ↔ ) = ( ↔ )
[83]	Alternated square ↔		-
Scaliform	Snub order-4 square		-
Nonuniform			-
Nonuniform			-
Nonsimplectic	( ↔ ) = ( ↔ )
Nonuniform	Snub square ↔ ↔	(3.3.4.3.4)	(3.3.3)	(3.3.4.3.4)	(3.3.4.3.4)	+(3.3.3)

[6,3^1,1] family

There are 11 forms (and only 4 not shared with [6,3,4] family), generated by ring permutations of the Coxeter group: [6,3^1,1] or .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	0'	3
87	alternated order-6 cubic ↔	-	-	(∞) (3.3.3.3.3)	(∞) (3.3.3)	(3.6.3.6)
88	cantic order-6 cubic ↔	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.6)
89	runcic order-6 cubic ↔	(1) (6.6.6)	-	(3) (3.4.6.4)	(1) (3.3.3)
90	runcicantic order-6 cubic ↔	(1) (3.12.12)	-	(2) (4.6.12)	(1) (3.6.6)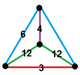
[16]	order-4 hexagonal ↔	(4) (6.6.6)	-	(4) (6.6.6)	-	(3.3.3.3)
[17]	rectified order-4 hexagonal ↔	(2) (3.6.3.6)	-	(2) (3.6.3.6)	(2) (3.3.3.3)
[18]	rectified order-6 cubic ↔	(1) (3.3.3.3.3)	-	(1) (3.3.3.3.3)	(6) (3.4.3.4)
[20]	truncated order-4 hexagonal ↔	(2) (3.12.12)	-	(2) (3.12.12)	(1) (3.3.3.3)
[21]	bitruncated order-6 cubic ↔	(1) (6.6.6)	-	(1) (6.6.6)	(2) (4.6.6)
[24]	cantellated order-6 cubic ↔	(1) (3.4.6.4)	(2) (4.4.4)	(1) (3.4.6.4)	(1) (3.4.3.4)
[27]	cantitruncated order-6 cubic ↔	(1) (4.6.12)	(1) (4.4.4)	(1) (4.6.12)	(1) (4.6.6)

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	0'	3	Alt
[141]	alternated order-4 hexagonal ↔ ↔ ↔						(4.6.6)
Nonuniform	bisnub order-4 hexagonal ↔
Nonuniform	snub rectified order-4 hexagonal ↔	(3.3.3.3.6)	(3.3.3)	(3.3.3.3.6)	(3.3.3.3.3)	+(3.3.3)

Cyclic graphs

[(4,4,3,3)] family

There are 11 forms, 4 unique to this family, generated by ring permutations of the Coxeter group: , with ↔ .

#	Honeycomb name Coxeter diagram	Cells by location				Vertex figure	Picture
		0	1	2	3
91	tetrahedral-square	-	(6) (444)	(8) (333)	(12) (3434)	(3444)
92	cyclotruncated square-tetrahedral	(444)	(488)	(333)	(388)
93	cyclotruncated tetrahedral-square	(1) (3333)	(1) (444)	(4) (366)	(4) (466)
94	truncated tetrahedral-square	(1) (3444)	(1) (488)	(1) (366)	(2) (468)
[64]	( ↔ ) = rectified order-4 octahedral	(3434)	(4444)	(3434)	(3434)
[65]	( ↔ ) = order-4 octahedral	(3333)	-	(3333)	(3333)
[67]	( ↔ ) = truncated order-4 octahedral	(466)	(4444)	(3434)	(466)
[83]	alternated square ( ↔ ) =	(444)	(4444)	-	(444)	(4.3.4.3)
[84]	cantic square ( ↔ ) =	(388)	(488)	(3434)	(388)
[85]	runcic square ( ↔ ) =	(3444)	(3434)	(3333)	(3444)
[86]	runcicantic square ( ↔ ) =	(468)	(488)	(466)	(468)

#	Honeycomb name Coxeter diagram	Cells by location					Vertex figure	Picture
		0	1	2	3	Alt
Scaliform	snub order-4 octahedral = =		-	-		irr. {}v{4}
Nonuniform
Nonsimplectic	alternated tetrahedral-square ↔

[(4,4,4,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group: .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	2	3
95	cubic-square	(8) (4.4.4)	-	(6) (4.4.4.4)	(12) (4.4.4.4)	(3.4.4.4)
96	octahedral-square	(3.4.3.4)	(3.3.3.3)	-	(4.4.4.4)	(4.4.4.4)
97	cyclotruncated cubic-square	(4) (3.8.8)	(1) (3.3.3.3)	(1) (4.4.4.4)	(4) (4.8.8)
98	cyclotruncated square-cubic	(1) (4.4.4)	(1) (4.4.4)	(3) (4.8.8)	(3) (4.8.8)
99	cyclotruncated octahedral-square	(4) (4.6.6)	(4) (4.6.6)	(1) (4.4.4.4)	(1) (4.4.4.4)
100	rectified cubic-square	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (4.4.4.4)	(2) (4.4.4.4)
101	truncated cubic-square	(1) (4.8.8)	(1) (3.4.4.4)	(2) (4.8.8)	(1) (4.8.8)
102	truncated octahedral-square	(2) (4.6.8	(1) (4.6.6)	(1) (4.4.4.4)	(1) (4.8.8)
103	omnitruncated octahedral-square	(1) (4.6.8)	(1) (4.6.8)	(1) (4.8.8)	(1) (4.8.8)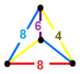

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure
		0	1	2	3	Alt
Nonsimplectic	alternated cubic-square ↔	-				(3.4.4.4)
Nonuniform	snub octahedral-square
Nonuniform	cyclosnub square-cubic
Nonuniform	cyclosnub octahedral-square
Nonuniform	omnisnub cubic-square	(3.3.3.3.4)	(3.3.3.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	+(3.3.3)

[(4,4,4,4)] family

There are 5 forms, 1 unique, generated by ring permutations of the Coxeter group: . Repeat constructions are related as: ↔ , ↔ , and ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	2	3
104	quarter order-4 square ↔	(4.8.8)	(4.4.4.4)	(4.4.4.4)	(4.8.8)
[62]	square ↔ ↔	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)
[77]	order-4 square ( ↔ ) =	(4.4.4.4)	-	(4.4.4.4)	(4.4.4.4)	(4.4.4.4)
[78]	truncated order-4 square ( ↔ ) =	(4.8.8)	(4.4.4.4)	(4.8.8)	(4.8.8)
[79]	bitruncated order-4 square ↔	(4.8.8)	(4.8.8)	(4.8.8)	(4.8.8)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure
		0	1	2	3	Alt
[83]	alternated square ( ↔ ↔ ) =	(6) (4.4.4.4)	(6) (4.4.4.4)	(6) (4.4.4.4)	(6) (4.4.4.4)	(8) (4.4.4)	(4.3.4.3)
Nonsimplectic	alternated order-4 square ↔		-
Nonsimplectic	cantic order-4 square ↔
Nonuniform	cyclosnub square
Nonuniform	snub order-4 square
Nonuniform	bisnub order-4 square ↔	(3.3.4.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	(3.3.4.3.4)	+(3.3.3)

[(6,3,3,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group: .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure
		0	1	2	3
105	tetrahedral-hexagonal	(4) (3.3.3)	-	(4) (6.6.6)	(6) (3.6.3.6)	(3.4.3.4)
106	tetrahedral-triangular	(3.3.3.3)	(3.3.3)	-	(3.3.3.3.3.3)	(3.4.6.4)
107	cyclotruncated tetrahedral-hexagonal	(3) (3.6.6)	(1) (3.3.3)	(1) (6.6.6)	(3) (6.6.6)
108	cyclotruncated hexagonal-tetrahedral	(1) (3.3.3)	(1) (3.3.3)	(4) (3.12.12)	(4) (3.12.12)
109	cyclotruncated tetrahedral-triangular	(6) (3.6.6)	(6) (3.6.6)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
110	rectified tetrahedral-hexagonal	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.6.3.6)	(2) (3.4.6.4)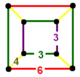
111	truncated tetrahedral-hexagonal	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.12.12)	(2) (4.6.12)
112	truncated tetrahedral-triangular	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.6.4)	(1) (6.6.6)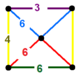
113	omnitruncated tetrahedral-hexagonal	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.12)	(1) (4.6.12)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure
		0	1	2	3	Alt
Nonuniform	omnisnub tetrahedral-hexagonal	(3.3.3.3.3)	(3.3.3.3.3)	(3.3.3.3.6)	(3.3.3.3.6)	+(3.3.3)

[(6,3,4,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure
		0	1	2	3
114	octahedral-hexagonal	(6) (3.3.3.3)	-	(8) (6.6.6)	(12) (3.6.3.6)
115	cubic-triangular	(∞) (3.4.3.4)	(∞) (4.4.4)	-	(∞) (3.3.3.3.3.3)	(3.4.6.4)
116	cyclotruncated octahedral-hexagonal	(3) (4.6.6)	(1) (4.4.4)	(1) (6.6.6)	(3) (6.6.6)
117	cyclotruncated hexagonal-octahedral	(1) (3.3.3.3)	(1) (3.3.3.3)	(4) (3.12.12)	(4) (3.12.12)
118	cyclotruncated cubic-triangular	(6) (3.8.8)	(6) (3.8.8)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
119	rectified octahedral-hexagonal	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.6.3.6)	(2) (3.4.6.4)
120	truncated octahedral-hexagonal	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.12.12)	(2) (4.6.12)
121	truncated cubic-triangular	(2) (4.6.8)	(1) (3.8.8)	(1) (3.4.6.4)	(1) (6.6.6)
122	omnitruncated octahedral-hexagonal	(1) (4.6.8)	(1) (4.6.8)	(1) (4.6.12)	(1) (4.6.12)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure
		0	1	2	3	Alt
Nonuniform	cyclosnub octahedral-hexagonal	(3.3.3.3.3)	(3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	irr. {3,4}
Nonuniform	omnisnub octahedral-hexagonal	(3.3.3.3.4)	(3.3.3.3.4)	(3.3.3.3.6)	(3.3.3.3.6)	irr. {3,3}

[(6,3,5,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	2	3
123	icosahedral-hexagonal	(6) (3.3.3.3.3)	-	(8) (6.6.6)	(12) (3.6.3.6)	3.4.5.4
124	dodecahedral-triangular	(30) (3.5.3.5)	(20) (5.5.5)	-	(12) (3.3.3.3.3.3)	(3.4.6.4)
125	cyclotruncated icosahedral-hexagonal	(3) (5.6.6)	(1) (5.5.5)	(1) (6.6.6)	(3) (6.6.6)
126	cyclotruncated hexagonal-icosahedral	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(5) (3.12.12)	(5) (3.12.12)
127	cyclotruncated dodecahedral-triangular	(6) (3.10.10)	(6) (3.10.10)	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)
128	rectified icosahedral-hexagonal	(1) (3.5.3.5)	(2) (3.4.5.4)	(1) (3.6.3.6)	(2) (3.4.6.4)
129	truncated icosahedral-hexagonal	(1) (5.6.6)	(1) (3.5.5.5)	(1) (3.12.12)	(2) (4.6.12)
130	truncated dodecahedral-triangular	(2) (4.6.10)	(1) (3.10.10)	(1) (3.4.6.4)	(1) (6.6.6)
131	omnitruncated icosahedral-hexagonal	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.12)	(1) (4.6.12)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	2	3	Alt
Nonuniform	omnisnub icosahedral-hexagonal	(3.3.3.3.5)	(3.3.3.3.5)	(3.3.3.3.6)	(3.3.3.3.6)	+(3.3.3)

[(6,3,6,3)] family

There are 6 forms, generated by ring permutations of the Coxeter group: .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	2	3
132	hexagonal-triangular	(3.3.3.3.3.3)	-	(6.6.6)	(3.6.3.6)	(3.4.6.4)
133	cyclotruncated hexagonal-triangular	(1) (3.3.3.3.3.3)	(1) (3.3.3.3.3.3)	(3) (3.12.12)	(3) (3.12.12)
134	cyclotruncated triangular-hexagonal	(1) (3.6.3.6)	(2) (3.4.6.4)	(1) (3.6.3.6)	(2) (3.4.6.4)
135	rectified hexagonal-triangular	(1) (6.6.6)	(1) (3.4.6.4)	(1) (3.12.12)	(2) (4.6.12)
136	truncated hexagonal-triangular	(1) (4.6.12)	(1) (4.6.12)	(1) (4.6.12)	(1) (4.6.12)
[16]	order-4 hexagonal tiling =	(3) (6.6.6)	(1) (6.6.6)	(1) (6.6.6)	(3) (6.6.6)	(3.3.3.3)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	2	3	Alt
[141]	alternated order-4 hexagonal ↔ ↔ ↔	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(3.3.3.3.3.3)	+(3.3.3.3)	(4.6.6)
Nonuniform	cyclocantisnub hexagonal-triangular
Nonuniform	cycloruncicantisnub hexagonal-triangular
Nonuniform	snub rectified hexagonal-triangular	(3.3.3.3.6)	(3.3.3.3.6)	(3.3.3.3.6)	(3.3.3.3.6)	+(3.3.3)

Loop-n-tail graphs

[3,3^[3]] family

There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [3,3^[3]] or . 7 are half symmetry forms of [3,3,6]: ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
		0	1	0'	3
137	alternated hexagonal ( ↔ ) =	-	-	(3.3.3)	(3.3.3.3.3.3)	(3.6.6)
138	cantic hexagonal ↔	(1) (3.3.3.3)	-	(2) (3.6.6)	(2) (3.6.3.6)
139	runcic hexagonal ↔	(1) (4.4.4)	(1) (4.4.3)	(3) (3.4.3.4)	(1) (3.3.3.3.3.3)
140	runcicantic hexagonal ↔	(1) (3.10.10)	(1) (4.4.3)	(2) (4.6.6)	(1) (3.6.3.6)
[2]	rectified hexagonal ↔	(1) (3.3.3)	-	(1) (3.3.3)	(6) (3.6.3.6)	Triangular prism
[3]	rectified order-6 tetrahedral ↔	(2) (3.3.3.3)	-	(2) (3.3.3.3)	(2) (3.3.3.3.3.3)	Hexagonal prism
[4]	order-6 tetrahedral ↔	(4) (4.4.4)	-	(4) (4.4.4)	-
[8]	cantellated order-6 tetrahedral ↔	(1) (3.3.3.3)	(2) (4.4.6)	(1) (3.3.3.3)	(1) (3.6.3.6)
[9]	bitruncated order-6 tetrahedral ↔	(1) (3.6.6)	-	(1) (3.6.6)	(2) (6.6.6)
[10]	truncated order-6 tetrahedral ↔	(2) (3.10.10)	-	(2) (3.10.10)	(1) (3.6.3.6)
[14]	cantitruncated order-6 tetrahedral ↔	(1) (4.6.6)	(1) (4.4.6)	(1) (4.6.6)	(1) (6.6.6)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure
		0	1	0'	3	Alt
Nonuniform	snub rectified order-6 tetrahedral ↔	(3.3.3.3.3)	(3.3.3.3)	(3.3.3.3.3)	(3.3.3.3.3.3)	+(3.3.3)

[4,3^[3]] family

There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [4,3^[3]] or . 7 are half symmetry forms of [4,3,6]: ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
		0	1	0'	3
141	alternated order-4 hexagonal ↔	-	-	(3.3.3.3)	(3.3.3.3.3.3)	(4.6.6)
142	cantic order-4 hexagonal ↔ ↔	(1) (3.4.3.4)	-	(2) (4.6.6)	(2) (3.6.3.6)
143	runcic order-4 hexagonal ↔	(1) (4.4.4)	(1) (4.4.3)	(3) (3.4.4.4)	(1) (3.3.3.3.3.3)
144	runcicantic order-4 hexagonal ↔	(1) (3.8.8)	(1) (4.4.3)	(2) (4.6.8)	(1) (3.6.3.6)
[16]	order-4 hexagonal ↔	(4) (4.4.4)	-	(4) (4.4.4)	-
[17]	rectified order-4 hexagonal ↔	(1) (3.3.3.3)	-	(1) (3.3.3.3)	(6) (3.6.3.6)
[18]	rectified order-6 cubic ↔	(2) (3.4.3.4)	-	(2) (3.4.3.4)	(2) (3.3.3.3.3.3)
[21]	bitruncated order-4 hexagonal ↔	(1) (4.6.6)	-	(1) (4.6.6)	(2) (6.6.6)
[22]	truncated order-6 cubic ↔	(2) (3.8.8)	-	(2) (3.8.8)	(1) (3.6.3.6)
[23]	cantellated order-4 hexagonal ↔	(1) (3.4.4.4)	(2) (4.4.6)	(1) (3.4.4.4)	(1) (3.6.3.6)
[26]	cantitruncated order-4 hexagonal ↔	(1) (4.6.8)	(1) (4.4.6)	(1) (4.6.8)	(1) (6.6.6)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure
		0	1	0'	3	Alt
Nonuniform	snub rectified order-4 hexagonal ↔	(3.3.3.3.4)	(3.3.3.3)	(3.3.3.3.4)	(3.3.3.3.3.3)	+(3.3.3)

[5,3^[3]] family

There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [5,3^[3]] or . 7 are half symmetry forms of [5,3,6]: ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
		0	1	0'	3
145	alternated order-5 hexagonal ↔	-	-	(3.3.3.3.3)	(3.3.3.3.3.3)	(3.6.3.6)
146	cantic order-5 hexagonal ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.3.6)
147	runcic order-5 hexagonal ↔	(1) (5.5.5)	(1) (4.4.3)	(3) (3.4.5.4)	(1) (3.3.3.3.3.3)
148	runcicantic order-5 hexagonal ↔	(1) (3.10.10)	(1) (4.4.3)	(2) (4.6.10)	(1) (3.6.3.6)
[32]	rectified order-5 hexagonal ↔	(1) (3.3.3.3.3)	-	(1) (3.3.3.3.3)	(6) (3.6.3.6)
[33]	rectified order-6 dodecahedral ↔	(2) (3.5.3.5)	-	(2) (3.5.3.5)	(2) (3.3.3.3.3.3)
[34]	Order-5 hexagonal ↔	(4) (5.5.5)	-	(4) (5.5.5)	-
[35]	truncated order-6 dodecahedral ↔	(2) (3.10.10)	-	(2) (3.10.10)	(1) (3.6.3.6)
[38]	cantellated order-5 hexagonal ↔	(1) (3.4.5.4)	(2) (6.4.4)	(1) (3.4.5.4)	(1) (3.6.3.6)
[39]	bitruncated order-5 hexagonal ↔	(1) (5.6.6)	-	(1) (5.6.6)	(2) (6.6.6)
[44]	cantitruncated order-5 hexagonal ↔	(1) (4.6.10)	(1) (6.4.4)	(1) (4.6.10)	(1) (6.6.6)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure	Picture
		0	1	0'	3	Alt
Nonuniform	snub rectified order-5 hexagonal ↔	(3.3.3.3.5)	(3.3.3)	(3.3.3.3.5)	(3.3.3.3.3.3)	+(3.3.3)

[6,3^[3]] family

There are 11 forms, 4 unique, generated by ring permutations of the Coxeter group: [6,3^[3]] or . 7 are half symmetry forms of [6,3,6]: ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				vertex figure	Picture
		0	1	0'	3
149	runcic order-6 hexagonal ↔	(1) (6.6.6)	(1) (4.4.3)	(3) (3.4.6.4)	(1) (3.3.3.3.3.3)
150	runcicantic order-6 hexagonal ↔	(1) (3.12.12)	(1) (4.4.3)	(2) (4.6.12)	(1) (3.6.3.6)
[1]	hexagonal ↔ ↔ ↔	(1) (6.6.6)	-	(1) (6.6.6)	(2) (6.6.6)
[46]	order-6 hexagonal ↔	(4) (6.6.6)	-	(4) (6.6.6)	-
[47]	rectified order-6 hexagonal ↔	(2) (3.6.3.6)	-	(2) (3.6.3.6)	(2) (3.3.3.3.3.3)
[47]	rectified order-6 hexagonal ↔	(1) (3.3.3.3.3.3)	-	(1) (3.3.3.3.3.3)	(6) (3.6.3.6)
[48]	truncated order-6 hexagonal ↔	(2) (3.12.12)	-	(2) (3.12.12)	(1) (3.3.3.3.3.3)
[49]	cantellated order-6 hexagonal ↔	(1) (3.4.6.4)	(2) (6.4.4)	(1) (3.4.6.4)	(1) (3.6.3.6)
[51]	cantitruncated order-6 hexagonal ↔	(1) (4.6.12)	(1) (6.4.4)	(1) (4.6.12)	(1) (6.6.6)
[54]	triangular tiling honeycomb ( ↔ ) =	-	-	(3.3.3.3.3.3)	(3.3.3.3.3.3)	(6.6.6)
[55]	cantic order-6 hexagonal ( ↔ ) =	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)

Alternated forms

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					vertex figure	Picture
		0	1	0'	3	Alt
[54]	triangular tiling honeycomb ( ↔ ↔ ) =		-		-		(6.6.6)
[137]	alternated hexagonal ( ↔ ) = ( ↔ )		-			+(3.6.6)	(3.6.6)
[47]	rectified order-6 hexagonal ↔ ↔ ↔	(3.6.3.6)	-	(3.6.3.6)	(3.3.3.3.3.3)
[55]	cantic order-6 hexagonal ( ↔ ) = ( ↔ ) =	(1) (3.6.3.6)	-	(2) (6.6.6)	(2) (3.6.3.6)
Nonuniform	snub rectified order-6 hexagonal ↔	(3.3.3.3.6)	(3.3.3.3)	(3.3.3.3.6)	(3.3.3.3.3.3)	+(3.3.3)

Multicyclic graphs

[3^{[ ]×[ ]}] family

There are 8 forms, 1 unique, generated by ring permutations of the Coxeter group: . Two are duplicated as ↔ , two as ↔ , and three as ↔ .

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)				Vertex figure	Picture
		0	1	2	3
151	Quarter order-4 hexagonal ↔
[17]	rectified order-4 hexagonal ↔ ↔ ↔					(4.4.4)
[18]	rectified order-6 cubic ↔ ↔ ↔					(6.4.4)
[21]	bitruncated order-6 cubic ↔ ↔ ↔
[87]	alternated order-6 cubic ↔ ↔	-				(3.6.3.6)
[88]	cantic order-6 cubic ↔ ↔
[141]	alternated order-4 hexagonal ↔ ↔		-			(4.6.6)
[142]	cantic order-4 hexagonal ↔ ↔

#	Honeycomb name Coxeter diagram	Cells by location (and count around each vertex)					Vertex figure	Picture
		0	1	2	3	Alt
Nonuniform	bisnub order-6 cubic ↔					irr. {3,3}

[3^[3,3]] family

There are 4 forms, 0 unique, generated by ring permutations of the Coxeter group: . They are repeated in four families: ↔ (index 2 subgroup), ↔ (index 4 subgroup), ↔ (index 6 subgroup), and ↔ (index 24 subgroup).

#	Name Coxeter diagram	0	1	2	3	vertex figure	Picture
[1]	hexagonal ↔					{3,3}
[47]	rectified order-6 hexagonal ↔					t{2,3}
[54]	triangular tiling honeycomb ( ↔ ) =		-			t{3[3]}
[55]	rectified triangular ↔					t{2,3}

#	Name Coxeter diagram	0	1	2	3	Alt	vertex figure	Picture
[137]	alternated hexagonal ( ↔ ) =	s{3[3]}	s{3[3]}	s{3[3]}	s{3[3]}	{3,3}	(4.6.6)

Summary enumerations by family

Linear graphs

Paracompact hyperbolic enumeration

Group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
${\displaystyle {\bar {R}}_{3}}$ [4,4,3]	[4,4,3]	15		[1+,4,1+,4,3+]	(6)	(↔ ) (↔ )
				[4,4,3]+	(1)
${\displaystyle {\bar {N}}_{3}}$ [4,4,4]	[4,4,4]	3		[1+,4,1+,4,1+,4,1+]	(3)	(↔ = )
	[4,4,4] ↔	(3)		[1+,4,1+,4,1+,4,1+]	(3)	(↔ )
	[2+[4,4,4]]	3		[2+[(4,4+,4,2+)]]	(2)
				[2+[4,4,4]]+	(1)
${\displaystyle {\bar {V}}_{3}}$ [6,3,3]	[6,3,3]	15		[1+,6,(3,3)+]	(2)	(↔ )
				[6,3,3]+	(1)
${\displaystyle {\bar {BV}}_{3}}$ [6,3,4]	[6,3,4]	15		[1+,6,3+,4,1+]	(6)	(↔ ) (↔ )
				[6,3,4]+	(1)
${\displaystyle {\bar {HV}}_{3}}$ [6,3,5]	[6,3,5]	15		[1+,6,(3,5)+]	(2)	(↔ )
				[6,3,5]+	(1)
${\displaystyle {\bar {Y}}_{3}}$ [3,6,3]	[3,6,3]	5
	[3,6,3] ↔	(1)		[2+[3+,6,3+]]	(1)
	[2+[3,6,3]]	3		[2+[3,6,3]]+	(1)
${\displaystyle {\bar {Z}}_{3}}$ [6,3,6]	[6,3,6]	6		[1+,6,3+,6,1+]	(2)	(↔ )
	[2+[6,3,6]] ↔	(1)		[2+[(6,3+,6,2+)]]	(2)
	[2+[6,3,6]]	2
				[2+[6,3,6]]+	(1)

Tridental graphs

Paracompact hyperbolic enumeration

Group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
${\displaystyle {\bar {DV}}_{3}}$ [6,31,1]	[6,31,1]	4
	[1[6,31,1]]=[6,3,4] ↔	(7)		[1[1+,6,31,1]]+	(2)	(↔ )
				[1[6,31,1]]+=[6,3,4]+	(1)
${\displaystyle {\bar {O}}_{3}}$ [3,41,1]	[3,41,1]	4		[3+,41,1]+	(2)	↔
	[1[3,41,1]]=[3,4,4] ↔	(7)		[1[3+,41,1]]+	(2)
				[1[3,41,1]]+	(1)
${\displaystyle {\bar {M}}_{3}}$ [41,1,1]	[41,1,1]	0	(none)
	[1[41,1,1]]=[4,4,4] ↔	(4)		[1[1+,4,1+,41,1]]+=[(4,1+,4,1+,4,2+)]	(4)	(↔ )
	[3[41,1,1]]=[4,4,3] ↔	(3)		[3[1+,41,1,1]]+=[1+,4,1+,4,3+]	(2)	(↔ )
				[3[41,1,1]]+=[4,4,3]+	(1)

Cyclic graphs

Paracompact hyperbolic enumeration

Group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
${\displaystyle {\widehat {CR}}_{3}}$ [(4,4,4,3)]	[(4,4,4,3)]	6		[(4,1+,4,1+,4,3+)]	(2)	↔
	[2+[(4,4,4,3)]]	3		[2+[(4,4+,4,3+)]]	(2)
				[2+[(4,4,4,3)]]+	(1)
${\displaystyle {\widehat {RR}}_{3}}$ [4[4]]	[4[4]]	(none)
	[2+[4[4]]]	1		[2+[(4+,4)[2]]]	(1)
	[1[4[4]]]=[4,41,1] ↔	(2)		[(1+,4)[4]]	(2)	↔
	[2[4[4]]]=[4,4,4] ↔	(1)		[2+[(1+,4,4)[2]]]	(1)
	[(2+,4)[4[4]]]=[2+[4,4,4]] =	(1)		[(2+,4)[4[4]]]+ = [2+[4,4,4]]+	(1)
${\displaystyle {\widehat {AV}}_{3}}$ [(6,3,3,3)]	[(6,3,3,3)]	6
	[2+[(6,3,3,3)]]	3		[2+[(6,3,3,3)]]+	(1)
${\displaystyle {\widehat {BV}}_{3}}$ [(3,4,3,6)]	[(3,4,3,6)]	6		[(3+,4,3+,6)]	(1)
	[2+[(3,4,3,6)]]	3		[2+[(3,4,3,6)]]+	(1)
${\displaystyle {\widehat {HV}}_{3}}$ [(3,5,3,6)]	[(3,5,3,6)]	6
	[2+[(3,5,3,6)]]	3		[2+[(3,5,3,6)]]+	(1)
${\displaystyle {\widehat {VV}}_{3}}$ [(3,6)[2]]	[(3,6)[2]]	2
	[2+[(3,6)[2]]]	1
	[2+[(3,6)[2]]]	1
	[2+[(3,6)[2]]] =	(1)		[2+[(3+,6)[2]]]	(1)
	[(2,2)+[(3,6)[2]]]	1		[(2,2)+[(3,6)[2]]]+	(1)

Paracompact hyperbolic enumeration

Group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
${\displaystyle {\widehat {BR}}_{3}}$ [(3,3,4,4)]	[(3,3,4,4)]	4
	[1[(4,4,3,3)]]=[3,41,1] ↔	(7)		[1[(3,3,4,1+,4)]]+ = [3+,41,1]+	(2)	(= )
				[1[(3,3,4,4)]]+ = [3,41,1]+	(1)
${\displaystyle {\bar {DP}}_{3}}$ [3[ ]x[ ]]	[3[ ]x[ ]]	1
	[1[3[ ]x[ ]]]=[6,31,1] ↔	(2)
	[1[3[ ]x[ ]]]=[4,3[3]] ↔	(2)
	[2[3[ ]x[ ]]]=[6,3,4] ↔	(3)		[2[3[ ]x[ ]]]+ =[6,3,4]+	(1)
${\displaystyle {\bar {PP}}_{3}}$ [3[3,3]]	[3[3,3]]	0	(none)
	[1[3[3,3]]]=[6,3[3]] ↔	0	(none)
	[3[3[3,3]]]=[3,6,3] ↔	(2)
	[2[3[3,3]]]=[6,3,6] ↔	(1)
	[(3,3)[3[3,3]]]=[6,3,3] =	(1)		[(3,3)[3[3,3]]]+ = [6,3,3]+	(1)

Loop-n-tail graphs

Symmetry in these graphs can be doubled by adding a mirror: [1[n,3^[3]]] = [n,3,6]. Therefore ring-symmetry graphs are repeated in the linear graph families.

Paracompact hyperbolic enumeration

Group	Extended symmetry	Honeycombs		Chiral extended symmetry	Alternation honeycombs
${\displaystyle {\bar {P}}_{3}}$ [3,3[3]]	[3,3[3]]	4
	[1[3,3[3]]]=[3,3,6] ↔	(7)		[1[3,3[3]]]+ = [3,3,6]+	(1)
${\displaystyle {\bar {BP}}_{3}}$ [4,3[3]]	[4,3[3]]	4
	[1[4,3[3]]]=[4,3,6] ↔	(7)		[1+,4,(3[3])+]	(2)	↔
				[4,3[3]]+	(1)
${\displaystyle {\bar {HP}}_{3}}$ [5,3[3]]	[5,3[3]]	4
	[1[5,3[3]]]=[5,3,6] ↔	(7)		[1[5,3[3]]]+ = [5,3,6]+	(1)
${\displaystyle {\bar {VP}}_{3}}$ [6,3[3]]	[6,3[3]]	2
	[6,3[3]] =	(2)	( ↔ ) ( = )
	[(3,3)[1+,6,3[3]]]=[6,3,3] ↔ ↔	(1)		[(3,3)[1+,6,3[3]]]+	(1)
	[1[6,3[3]]]=[6,3,6] ↔	(6)		[3[1+,6,3[3]]]+ = [3,6,3]+	(1)	↔ (= )
				[1[6,3[3]]]+ = [6,3,6]+	(1)

See also

• Uniform tilings in hyperbolic plane
• List of regular polytopes#Tessellations of hyperbolic 3-space

Notes

References

• James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN99-35678, ISBN0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)
• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I,II)
• Coxeter Decompositions of Hyperbolic Tetrahedra, arXiv/PDF, A. Felikson, December 2002
• C. W. L. Garner, Regular Skew Polyhedra in Hyperbolic Three-Space Can. J. Math. 19, 1179-1186, 1967. PDF [1]
• Norman Johnson, Geometries and Transformations, (2018) Chapters 11,12,13
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [2] [3]
• N.W. Johnson, R. Kellerhals, J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H³: p130. [4]
• Klitzing, Richard. "Hyperbolic honeycombs H3 paracompact".