큐브 연결 사이클

Cube-connected cycles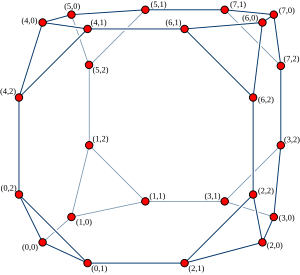
오더 3의 큐브 연결 사이클로, 잘린 큐브의 꼭지점에 기하학적으로 배열한다.

그래프 이론에서 큐브 연결 주기는 하이퍼큐브 그래프의 각 꼭지점을 사이클로 교체하여 형성된 비방향 입방 그래프다.Prepata & Vuillemin(1981)이 병렬 컴퓨팅에서 네트워크 토폴로지로 사용하기 위해 도입했다.

정의

주문 n(표시 CCCn)의cube-connected 주기가 0≤)<>그래프를 n2n 노드 집합 중에서 형성된, 숫자의 쌍에 의해 인덱싱 되(), y), 2n고 0≤ y<>로 n. 정의될 수 있그러한 각각의 노드 셋의 이웃:mod(x(y+1)nx에,)mod n(x(y− 1),()⊕ 2y, y),"⊕"이진 숫자를 비트 또는 연산이 독점적인을 의미한다 연결되어 있다..

이 그래프는 n차원 하이퍼큐브 그래프의 각 꼭지점을 n-vertex 사이클로 교체한 결과로도 해석할 수 있다.하이퍼큐브 그래프 정점은 숫자 x에 의해 색인되고, 각 사이클 내의 위치는 숫자 y에 의해 색인화된다.

특성.

order n의 큐브 연결 사이클은 단어의 회전과 플립 비트에 의해 길이가 n인 이항 단어에 작용하는 그룹의 Cayley 그래프다.[1]그룹에서 이 Cayley 그래프를 형성하는 데 사용되는 발전기는 단어를 한 위치 왼쪽으로 회전시키거나 한 위치 오른쪽으로 회전시키거나 첫 비트를 뒤집어서 작용하는 그룹 요소들이다.그것은 Cayley 그래프이기 때문에, 그것은 정점 변환이다: 어떤 정점을 다른 정점에 매핑하는 그래프의 대칭성이 있다.

순서 n의 입방체 연결 주기 지름은 2n + +n/2⌋ - 2이며, (x, y)로부터 가장 먼 점은 (2n - x - 1, (y + n/2) mod n)[2]이다.Sýkora & Vrťo(1993)는 CCC의n 교차번호는 (1/20) + o(1) 4n.

로바즈 추측에 따르면 큐브 연결 사이클 그래프에는 항상 해밀턴 사이클이 포함되어야 하며, 현재 이것은 사실로 알려져 있다.더 일반적으로, 비록 이러한 그래프들이 범순환은 아니지만, 그것들은 가능한 짝수 길이의 경계를 제외한 모든 주기의 주기를 포함하고, n이 홀수일 때는 가능한 홀수 길이의 많은 주기도 포함하고 있다.[3]

병렬 처리 응용 프로그램

큐브 연결 사이클은 Prepata & Vuillemin(1981)에 의해 조사되었는데, 그는 이 그래프를 병렬 컴퓨터에서 프로세서를 연결하는 네트워크의 상호 접속 패턴으로 적용했다.이 애플리케이션에서 큐브 연결 주기는 프로세서당 3개의 연결만 필요로 하는 반면 하이퍼큐브의 연결 장점을 가지고 있다.Prepyata와 Vuillemin은 이 네트워크를 기반으로 하는 평면 배치가 많은 병렬 처리 작업에 대해 최적의 면적 × 시간2 복잡성을 가지고 있다는 것을 보여주었다.

메모들

  1. ^ Akers & Crishnamurthy (1989년); Annexstein, Baumslag & Rosenberg (1990년)
  2. ^ 프리시, 하벨 & 리블(1997)
  3. ^ 게르마, 헤이데만 & 소토(1998)

참조

  • Akers, Sheldon B.; Krishnamurthy, Balakrishnan (1989), "A group-theoretic model for symmetric interconnection networks", IEEE Transactions on Computers, 38 (4): 555–566, doi:10.1109/12.21148.
  • Annexstein, Fred; Baumslag, Marc; Rosenberg, Arnold L. (1990), "Group action graphs and parallel architectures", SIAM Journal on Computing, 19 (3): 544–569, doi:10.1137/0219037.
  • Friš, Ivan; Havel, Ivan; Liebl, Petr (1997), "The diameter of the cube-connected cycles", Information Processing Letters, 61 (3): 157–160, doi:10.1016/S0020-0190(97)00013-6.
  • Germa, Anne; Heydemann, Marie-Claude; Sotteau, Dominique (1998), "Cycles in the cube-connected cycles graph", Discrete Applied Mathematics, 83 (1–3): 135–155, doi:10.1016/S0166-218X(98)80001-2, MR 1622968.
  • Preparata, Franco P.; Vuillemin, Jean (1981), "The cube-connected cycles: a versatile network for parallel computation", Communications of the ACM, 24 (5): 300–309, doi:10.1145/358645.358660, hdl:2142/74219.
  • Sýkora, Ondrej; Vrťo, Imrich (1993), "On crossing numbers of hypercubes and cube connected cycles", BIT Numerical Mathematics, 33 (2): 232–237, doi:10.1007/BF01989746, hdl:11858/00-001M-0000-002D-92E4-9.