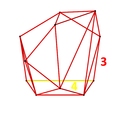
런케이티드 24셀
Runcinated 24-cells 24셀 |  런케이티드 24셀 |
 24-셀 런시 셀 |  전지 24셀 (Runcicantitruntrunturn 24-cell) |
| F4 Coxeter 평면의 직교 투영 | |
|---|---|
4차원 기하학에서 런케이티드 24 셀은 볼록한 균일한 4 폴리토프로서 일반 24 셀의 런케이닝(제3의 순서 절단)이다.
24-셀에는 순열 자르기와 운율을 포함하여 3개의 독특한 운율이 있다.
런케이티드 24셀
| 런케이티드 24셀 | ||
| 유형 | 제복4폴리토프 | |
| 슐레플리 기호 | t0,3{3,4,3} | |
| 콕시터 다이어그램 | ||
| 세포 | 240 | 48 3.3.3.3 192 3.4.4 |
| 얼굴 | 672 | 384{3} 288{4} |
| 가장자리 | 576 | |
| 정점 | 144 | |
| 정점수 |  길쭉한 사각 반감 | |
| 대칭군 | 자동(F4), [3,4,3], 주문 2304 | |
| 특성. | 볼록한, 가장자리-변환성 | |
| 균일지수 | 25 26 27 | |
기하학에서 런케이티드 24셀 또는 작은 프리즘타테트라콘토라콘은 48옥타헤드라와 192개의 삼각 프리즘으로 경계된 균일한 4폴리토프다.팔면체세포는 24세포의 세포와 그 이중과 일치한다.
E. L. Elte는 1912년에 그것을 반정형 폴리토프로 확인했다.
대체 이름
- 런케이티드 24셀(노르만 W. 존슨)
- 룬케티드이코시테트라초론
- 런케이트 폴리오크헤드론
- 작은 프리즘토테콘토락타코론(스픽) (조나단 보우어스)
좌표
에지 길이가 2인 런케이티드 24 셀의 데카르트 좌표는 다음 부호의 모든 순열과 좌표에 의해 주어진다.
- (0, 0, √2, 2+√2)
- (1, 1, 1+√2, 1+√2)
두 번째 좌표 세트의 순열은 새겨진 칸막이의 정점과 일치한다.
투영
| 콕시터 평면 | F4 | B4 |
|---|---|---|
| 그래프 |  |  |
| 치측 대칭 | [[12]] = [24] | [8] |
| 콕시터 평면 | B3 / A2 | B2 / A3 |
| 그래프 |  |  |
| 치측 대칭 | [6] | [[4]] = [8] |
| 3D 투시 투영 | ||
|---|---|---|
 팔면체 중심의 슐레겔 도표와 팔면체도가 표시된다. |  런케이티드 24 셀의 원근 투영법은 팔면 셀을 중심으로 3차원으로 한다. 회전은 구조를 보여주기 위해 3D 영상의 일부일 뿐, 4-공간에서의 회전은 아니다.4D 시점으로 향하는 팔면체 중 15개가 빨간색으로 표시되어 있다.그들 사이의 간격은 삼각 프리즘의 틀로 채워진다. |  48개의 팔면체 세포 중 24개를 이용한 입체 투영 |
관련정규다면체
일반 스큐 다면체, {4,8 3}은(는) 지그재그하는 비 평면 정점 그림에서 각 꼭지점 둘레에 8제곱이 있는 4공간으로 존재한다.이러한 사각형 면은 576개의 가장자리와 288개의 꼭지점을 모두 사용하여 런케이티드 24-셀에서 볼 수 있다.런케이티드 24셀의 384개의 삼각형 면은 제거된 것으로 볼 수 있다.이중 정사각형 다면체, {8,4 3}은 비트코인 24셀의 팔각면과 유사하게 관련이 있다.
24-셀 런시 셀
| 24-셀 런시 셀 | ||
| 유형 | 제복4폴리토프 | |
| 슐레플리 기호 | t0,1,3{3,4,3} s2,3{3,4,3} | |
| 콕시터 다이어그램 | ||
| 세포 | 240 | 24 4.6.6 96 4.4.6 96 3.4.4 24 3.4.4.4 |
| 얼굴 | 1104 | 192{3} 720{4} 192{6} |
| 가장자리 | 1440 | |
| 정점 | 576 | |
| 정점수 |  사다리꼴 피라미드 | |
| 대칭군 | F4, [3,4,3], 주문 1152 | |
| 특성. | 볼록하게 하다 | |
| 균일지수 | 28 29 30 | |
24-셀 또는 프리즘토르혼방 이코시테트라초론은 24-셀에서 파생된 균일한 4-폴리토프다.24세포의 세포에 해당하는 잘린 옥타헤드라 24개, 롬비쿠옥타헤드라 24개, 이중 24세포의 세포와 일치하는 24개, 삼각 프리즘 96개, 육각 프리즘 96개로 경계를 이룬다.
좌표
에지 길이 2를 가진 24-셀의 원점 중심 런시트의 데카르트 좌표는 좌표와 부호의 모든 순열로 주어진다.
- (0, √2, 2√2, 2+3√2)
- (1, 1+√2, 1+2√2, 1+3√2)
두 번째 좌표 세트의 순열은 내접된 전위차 경계의 정점을 나타낸다.
이중 구성에는 모든 순열에서 생성된 좌표와 다음 징후가 있다.
- (1,1,1+√2,5+√2)
- (1,3,3+√2,3+√2)
- (2,2,2+√2,4+√2)
투영
| 콕시터 평면 | F4 | |
|---|---|---|
| 그래프 |  | |
| 치측 대칭 | [12] | |
| 콕시터 평면 | B3 / A2 (a) | B3 / A2 (b) |
| 그래프 |  |  |
| 치측 대칭 | [6] | [6] |
| 콕시터 평면 | B4 | B2 / A3 |
| 그래프 |  |  |
| 치측 대칭 | [8] | [4] |
 슐레겔 도표 롬비큐옥타헤드론을 중심으로 삼각 프리즘만 표시됨 |
런시칸틱 스너브 24세포
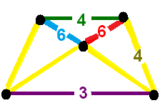
런시티가 있는 24셀(또는 런시칸텔링된 24셀)의 반대칭 구조는, 런시칸틱 스너브 24셀이라고도 하며, 로써는 기하학적으로 동일하지만, 삼각형 면은 더욱 세분화된다.스너브 24-셀과 마찬가지로 대칭 [3+,4,3], 순서 576이다.런시트가 있는 24셀은 192개의 동일한 육각면을 가지고 있고, 런시코틱 스너브 24셀은 2개의 건설적인 96개의 육각형을 가지고 있다.차이점은 정점 그림에서 확인할 수 있다.
 |  |
룬스크 스너브 24셀
| 룬스크 스너브 24셀 | ||
|---|---|---|
| 슐레플리 기호 | s3{3,4,3} | |
| 콕시터 다이어그램 | ||
| 세포 | 240 | 24 {3,5} 24 t{3,3} 96 (4.4.3) 96 삼류 |
| 얼굴 | 960 | 576 {3} 288 {4} 96 {6} |
| 가장자리 | 1008 | |
| 정점 | 288 | |
| 정점수 |  | |
| 대칭군 | [3+,4,3] 주문 576 | |
| 특성. | 볼록하게 하다 | |
관련 4-폴리토프는 런치 스너브 24-셀 또는 프리즘토르옴비즈니ub icositetrachoron, s3{3,4,3}. 균일하지는 않지만 정점 변환이며 모든 정규 폴리곤 얼굴을 가지고 있다.틈새에 이코사헤드라 24개, 잘린 사트라헤드라 24개, 삼각 프리즘 96개, 삼각 큐폴레 96개로 구성되어 있으며, 총 240개 셀, 960개 면, 1008개 모서리, 288개 꼭지점 등이 있다.스너브 24-셀과 마찬가지로 대칭 [3+,4,3], 순서 576이다.[1]
정점 모양은 고드름 1개, 삼각형 프리즘 2개, 잘린 사면체 1개, 삼각형 큐폴레 3개를 포함한다.
| 직교 투영 | 그물 | ||
|---|---|---|---|
 |  |  |  |
전지 24셀
| 전지 24셀 | ||
| 유형 | 제복4폴리토프 | |
| 슐레플리 기호 | t0,1,2,3{3,4,3} | |
| 콕시터 다이어그램 | ||
| 세포 | 240 | 48 (4.6.8) 192 (4.4.6) |
| 얼굴 | 1392 | 864{4} 384{6} 144{8} |
| 가장자리 | 2304 | |
| 정점 | 1152 | |
| 정점수 |  식물성 분산체 | |
| 대칭군 | 자동(F4), [3,4,3], 주문 2304 | |
| 특성. | 볼록하게 하다 | |
| 균일지수 | 29 30 31 | |
전집 24셀 또는 대 프리즘타테콘톡타코론은 24셀에서 파생된 균일한 4폴리토프다.정점 1152개, 가장자리 2304개, 면 1392개(사각형 864개, 육각 384개, 옥타곤 144개)로 구성되어 있다.그것은 240개의 세포를 가지고 있다: 잘린 큐보타헤드라 48개, 육각형 프리즘 192개.각 꼭지점에는 6각형의 프리즘 2개와 잘린 큐보타헤드라 2개의 식물성 분산 꼭지점 모양에 4개의 세포가 있다.
구조
잘린 48개의 칸옥타헤드랄 세포는 팔각형의 얼굴을 통해 서로 연결되어 있다.그것들은 각각 24개의 두 그룹으로 분류될 수 있고, 24개의 셀과 그것의 이중의 셀과 일치한다.이들 사이의 간격은 192개의 육각 프리즘으로 이루어진 네트워크에 의해 채워지고, 교대로 사각면을 통해 서로 연결되며, 육각면과 나머지 사각면을 통해 잘린 큐보타헤드라에 연결된다.
좌표
가장자리 길이 2를 가진 24-셀의 카르테시안 좌표는 모두 좌표 순열과 다음 부호의 표시들이다.
- (1, 1+√2, 1+2√2, 5+3√2)
- (1, 3+√2, 3+2√2, 3+3√2)
- (2, 2+√2, 2+2√2, 4+3√2)
이미지들
| 콕시터 평면 | F4 | B4 |
|---|---|---|
| 그래프 |  |  |
| 치측 대칭 | [[12]] = [24] | [8] |
| 콕시터 평면 | B3 / A2 | B2 / A3 |
| 그래프 |  |  |
| 치측 대칭 | [6] | [[4]] = [8] |
| 3D 투시 투영 | |
|---|---|
 슐레겔 도표 |  잘린 칸옥타헤드론 중심의 3D 투영법.4D 관점에서 가장 가까운 큰 롬비큐옥타헤드랄 세포는 빨간색으로 표시되며, 6개의 주변 큰 롬비큐옥타헤드라는 노란색으로 표시된다.가장 가까운 세포와 정사각형 면을 공유하는 육각형 프리즘 중 12개가 노란 세포와 함께 파란색으로 표시된다.나머지 세포는 녹색으로 표시된다.4D 관점에서 폴리포프의 저쪽에 놓여있는 세포들은 명확성을 위해 도태되었다. |
 전지 24셀 |  듀얼 - 옴니트런 24-셀 |
관련 폴리토페스
Nonuniform variants with [3,4,3] symmetry and two types of truncated cuboctahedra can be doubled by placing the two types of truncated cuboctahedra on each other to produce a nonuniform polychoron with 48 truncated cuboctahedra, 144 octagonal prisms (as ditetragonal trapezoprisms), 192 hexagonal prisms, two kinds of 864 rectangular trapezoprisms (2D2d 대칭의 88과 C2v 대칭의 576), 그리고 2304 정점.그것의 꼭지점 모양은 불규칙한 삼각형 두피라미드다.
그런 다음 이 폴리초론을 교대로 만들어 48개의 스너브 정사각형, 144개의 사각형 반격, 192개의 옥타헤드라(삼각형 반격), 2016년 3종류의 사다리꼴 디스페노이드, 576개의 필릭 디스프레노이드, 1152개의 불규칙 사다리꼴 반정맥, 1152개의 정점 등을 만들 수 있다.대칭은 [3,4,3],+ 순서 1152이다.
풀 스너브 24셀
균일한 스너브 24셀은 로서4 D 계열의 풀 스너브나 옴니스너브이긴 하지만 F 계열4 내의 콕시터 도표를 가지고 존 호튼 콘웨이에 의해 세미 스너브 24셀이라고 불린다.
이와는 대조적으로, 전분해 24 셀의 교대로 정의되는 완전한 스너브 24 셀 또는 전분해 24 셀은 균일하게 만들 수 없지만, 그것은 Coxeter 다이어그램과 대칭 [3,4,3],+ 순서 1152로, 48 스너브 입방체, 192 옥타헤드론, 576 사분해로 구성하여 정점을 삭제했다.그것의 꼭지점 모양은 4개의 4개, 2개의 8각형, 2개의 스너브 정사각형을 포함하고 있다.816개의 세포, 2832개의 면, 2592개의 가장자리, 576개의 꼭지점을 가지고 있다.[2]
관련 폴리토페스
| 24-셀 계열 폴리토페스 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 이름 | 24셀 | 잘린 24셀 | 24셀을 훔치다 | 정류 24세포 | 24세포로 알 수 있는 | 24구경. | 캔트런 24셀 | 윤택 24셀 | 24구경. | 전지 24셀 | |
| 슐레플리 심볼 | {3,4,3} | t0,1{3,4,3} t{3,4,3} | s{3,4,3} | t1{3,4,3} r{3,4,3} | t0,2{3,4,3} rr{3,4,3} | t1,2{3,4,3} 2t{3,4,3} | t0,1,2{3,4,3} tr{3,4,3} | t0,3{3,4,3} | t0,1,3{3,4,3} | t0,1,2,3{3,4,3} | |
| 콕시터 도표를 만들다 | |||||||||||
| 슐레겔 도표를 만들다 |  |  |  |  |  |  |  |  |  |  | |
| F4 |  |  |  |  |  |  |  |  |  |  | |
| B4 |  |  |  |  |  |  |  |  |  |  | |
| B3(a) |  |  |  |  |  |  |  |  |  |  | |
| B3(b) |  |  |  |  |  |  | |||||
| B2 |  |  |  |  |  |  |  |  |  |  | |
메모들
참조
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6
- (용지 22) H.S.M. Coxeter, 정규 및 반정규 다항체 I, [수학]Zeit. 46 (1940) 380-407, MR 2,10]
- (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
- (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
- J.H.콘웨이와 M.J.T. 가이: 4차원 아르키메데스 폴리토페스, 코펜하겐에서의 볼록성에 관한 콜로키움의 진행, 38페이지와 39페이지, 1965년
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
- 4차원 아르키메데스 폴리토페스(독일어), 마르코 뮐러, 2004년 박사 논문 [1] m58 m59 m53
- 3. icositetrachoron(24셀), George Olshevsky를 바탕으로 한 볼록한 균일한 폴리초라.
- Klitzing, Richard. "4D uniform polytopes (polychora)". x3o4o3x - spic, x3x4o3x - priico, s3s4o3x - prisi, x3x4x3x - gippic
| 가족 | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 다각형 | 삼각형 | 사각형 | p-곤 | 육각형 | 펜타곤 | |||||||
| 균일다면체 | 사면체 | 옥타헤드론 • 큐브 | 데미큐브 | 도데카헤드론 • 이코사헤드론 | ||||||||
| 균일 폴리초론 | 펜타코론 | 16-셀 • 테세락트 | 데미테세락트 | 24셀 | 120 셀 • 600 셀 | |||||||
| 제복5폴리토프 | 5와섹스 | 5정형 • 5정형 | 5데미큐브 | |||||||||
| 제복6폴리토프 | 6-630x | 6-정통 • 6-118 | 6데미큐브 | 122 • 221 | ||||||||
| 제복7폴리토프 | 7시 15분 | 7정맥 • 7정맥 | 7데미큐브 | 132 • 231 • 321 | ||||||||
| 제복8폴리토프 | 8시 15분 | 8정형 • 8정형 | 8데미큐브 | 142 • 241 • 421 | ||||||||
| 제복9폴리토프 | 9시 15분 | 9-정통 • 9-11 | 9데미큐브 | |||||||||
| 균일 10폴리토프 | 10센트짜리 | 10정형 • 10정형 | 10데미큐브 | |||||||||
| 균일 n폴리토프 | n-제곱스 | n-직관 • n-직관 | n-데미큐브 | 1k2 • 2k1 • k21 | n-자갈 폴리토프 | |||||||
| 주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록 | ||||||||||||