Strategic dominance

This article includes a list of general references, but it remains largely unverified because it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2016) (Learn how and when to remove this template message)

In game theory, strategic dominance (commonly called simply dominance) occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance. The opposite, intransitivity, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play.

Terminology

When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better. The result of the comparison is one of:

• B is equivalent to A: choosing B always gives the same outcome as choosing A, no matter what the other players do.
• B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other players do.
• B weakly dominates A: choosing B always gives at least as good an outcome as choosing A, no matter what the other players do, and there is at least one set of opponents' action for which B gives a better outcome than A. (Notice that if B strictly dominates A, then B weakly dominates A. Therefore, we can say "B dominates A" as synonymous of "B weakly dominates A".)^[1]
• B and A are intransitive: B and A are not equivalent, and B neither dominates, nor is dominated by, A. Choosing A is better in some cases, while choosing B is better in other cases, depending on exactly how the opponent chooses to play. For example, B is "throw rock" while A is "throw scissors" in Rock, Paper, Scissors.
• B는 A가 약하게 지배하고 있다: B가 A보다 더 나쁜 결과를 주는 적어도 한 세트의 상대적 행동이 있고, 반면에 다른 모든 일련의 상대적 행동들은 B와 같은 보상을 A에게 준다. (전략 A는 약하게 B를 지배한다.)
• B는 A가 엄격히 지배하고 있다. B를 선택하는 것은 다른 선수가 무엇을 하든 A를 선택하는 것보다 항상 더 나쁜 결과를 낳는다. (전략 A는 B를 엄격히 지배한다.)

이 개념은 두 전략의 비교를 넘어 일반화될 수 있다.

• 전략 B가 다른 가능한 모든 전략을 엄격하게 지배한다면 전략 B는 엄격히 지배적이다.
• 전략 B가 다른 가능한 모든 전략을 약하게 지배한다면 전략 B는 약하게 우세하다.
• 전략 B는 엄격하게 B를 지배하는 다른 전략이 존재한다면 엄격하게 지배된다.
• 전략 B는 약하게 B를 지배하는 다른 전략이 존재한다면 약하게 지배된다.

전략: 그 게임에서 선수를 위한 완전한 조건부 계획. 완전한 조건부 계획은 선수가 가능한 모든 결정 지점에서 취할 각 행동을 설명하는 선수의 행동의 완전한 사양이다. 정보 집합은 플레이어가 결정을 내려야 하는 게임에서 포인트를 나타내기 때문에 플레이어의 전략은 각 정보 집합에서 플레이어가 수행할 작업을 설명한다.^[2]

합리성: 각 플레이어가 자신이 가장 선호하는 것을 가져오도록 설계된 방식으로 행동한다는 가정; 폰 노이만과 모겐스턴은 이러한 선호가 특정 조건을 충족한다면 이는 수학적으로 보상의 극대화와 동등하다는 것을 보여주었다. 보상의 극대화를 위한 직접적인 예는 금전적 이득이지만, 게임 이론 분석의 목적상, 이 보상은 원하는 결과를 얻을 수 있다. 예를 들어, 현금 보상, 노력 또는 불편함의 최소화, 정의 증진 또는 전체적인 "유틸리티"의 축적과 같은 합리성의 가정은 참가자가 항상 다양한 가능한 결과 중 최선에서 최악의 순서로 순서를 가장 잘 충족하는 방식으로 행동할 것이라고 말한다.^[2]

상식: 각 플레이어가 게임에 대한 지식을 가지고 있고, 각 행동 과정과 관련된 규칙과 보답을 알고 있으며, 다른 모든 플레이어가 이와 같은 수준의 이해력을 가지고 있다는 가정을 하게 된다. 이것은 플레이어가 행동을 선택할 때 합리성을 가정하여 다른 플레이어의 행동에 대해 가치 판단을 할 수 있도록 하는 전제다.^[2]

Dominance and Nash equilibria

	C	D
C	1, 1	0, 0
D	0, 0	0, 0

If a strictly dominant strategy exists for one player in a game, that player will play that strategy in each of the game's Nash equilibria. If both players have a strictly dominant strategy, the game has only one unique Nash equilibrium. However, that Nash equilibrium is not necessarily "efficient", meaning that there may be non-equilibrium outcomes of the game that would be better for both players. The classic game used to illustrate this is the Prisoner's Dilemma.

Strictly dominated strategies cannot be a part of a Nash equilibrium, and as such, it is irrational for any player to play them. On the other hand, weakly dominated strategies may be part of Nash equilibria. For instance, consider the payoff matrix pictured at the right.

Strategy C weakly dominates strategy D. Consider playing C: If one's opponent plays C, one gets 1; if one's opponent plays D, one gets 0. Compare this to D, where one gets 0 regardless. Since in one case, one does better by playing C instead of D and never does worse, C weakly dominates D. Despite this, ${\displaystyle (D,D)}$ is a Nash equilibrium. Suppose both players choose D. Neither player will do any better by unilaterally deviating—if a player switches to playing C, they will still get 0. This satisfies the requirements of a Nash equilibrium. Suppose both players choose C. Neither player will do better by unilaterally deviating—if a player switches to playing D, they will get 0. This also satisfies the requirements of a Nash equilibrium.

Iterated elimination of strictly dominated strategies (IESDS)

The iterated elimination (or deletion) of dominated strategies (also denominated as IESDS or IDSDS) is one common technique for solving games that involves iteratively removing dominated strategies. In the first step, at most one dominated strategy is removed from the strategy space of each of the players since no rational player would ever play these strategies. This results in a new, smaller game. Some strategies—that were not dominated before—may be dominated in the smaller game. The first step is repeated, creating a new even smaller game, and so on. The process stops when no dominated strategy is found for any player. This process is valid since it is assumed that rationality among players is common knowledge, that is, each player knows that the rest of the players are rational, and each player knows that the rest of the players know that he knows that the rest of the players are rational, and so on ad infinitum (see Aumann, 1976).

이 과정에는 두 가지 버전이 있다. 한 가지 버전은 엄격하게 지배하는 전략만 제거하는 것을 포함한다. 이 과정을 마친 뒤 선수별로 전략이 하나뿐이라면 그 전략 세트는 독특한 나시 평형이다.^[3]

엄격한 우위 삭제 단계별 예:

1. C는 1번 선수에게 A가 엄격히 지배하고 있다. 따라서 플레이어 1은 결코 전략 C를 플레이하지 않을 것이다. 2번 선수도 이 사실을 알고 있다. (IESDS 그림 1 참조)
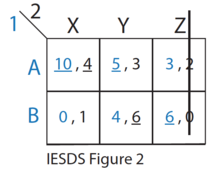
2. 나머지 전략(IESDS 그림 2 참조) 중 Z는 플레이어 2의 Y와 X가 엄격히 지배하고 있다. 따라서, 플레이어 2는 전략 Z를 절대로 플레이하지 않을 것이다. 1번 플레이어는 이것을 알고 있다.
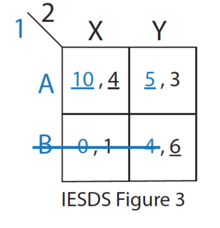
3. 나머지 전략(IESDS 그림 3 참조) 중 B는 플레이어 1의 경우 A가 엄격히 지배한다. 따라서 1번 플레이어는 절대 B를 플레이하지 않을 것이다. 2번 선수도 이 사실을 알고 있다.
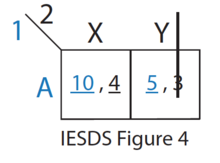
4. 나머지 전략(IESDS 그림 4 참조) 중 Y는 플레이어 2의 X에 의해 엄격히 지배된다. 따라서 2번 플레이어는 절대 Y를 플레이하지 않을 것이다. 1번 플레이어는 이것을 알고 있다.
5. 합리화할 수 있는 하나의 전략만이 {A,X}을(를) 남겨두고 있어 그 결과 (10,4)의 보수가 된다. 이것은 이 게임을 위한 싱글 나시 평형이다.

또 다른 버전은 엄격하게 그리고 약하게 지배하는 전략을 모두 제거하는 것을 포함한다. 그 과정이 끝날 때 각 선수에 대한 단일 전략이 있다면 이 전략 세트 역시 내시 평형이다. 그러나 첫 번째 과정과 달리 약하게 지배하는 전략을 제거하면 일부 나시 평준화가 제거될 수 있다. 결과적으로 약하게 지배하는 전략을 제거함으로써 발견되는 나시 평형만이 나시 평형만이 아닐 수도 있다. (일부 경기에서는 약하게 지배하는 전략을 다른 순서로 제거하면 결국 다른 나시 평형(Nash 평형)으로 끝날 수도 있다.)

취약한 우위 삭제 단계별 예:

1. O는 1번 선수에게 N이 엄격히 지배한다. 따라서, 플레이어 1은 전략 O를 결코 플레이하지 않을 것이다. 2번 선수도 이 사실을 알고 있다. (IESDS 그림 5 참조)
2. U는 2번 선수에게 T가 약하게 지배하고 있다. 플레이어 2가 T를 선택하면 최종 평형은 (N,T)

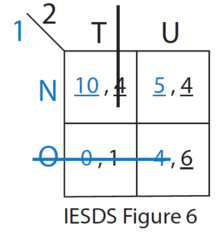
1. O는 1번 선수에게 N이 엄격히 지배한다. 따라서, 플레이어 1은 전략 O를 결코 플레이하지 않을 것이다. 2번 선수도 이 사실을 알고 있다. (IESDS 그림 6 참조)
2. T is weakly dominated by U for Player 2. If Player 2 chooses U, then the final equilibrium is (N,U)

In any case, if by iterated elimination of dominated strategies there is only one strategy left for each player, the game is called a dominance-solvable game.

Iterated elimination by mixed strategy

There are instances when there is no pure strategy that dominates another pure strategy, but a mixture of two or more pure strategies can dominate another strategy. This is called Strictly Dominant Mixed Strategies. If there is a mixture between two strategies or more that strictly dominates another strategy, then the last strategy should be eliminated immediately. Strictly dominated strategies are irrational, while pure strategies or mixed strategies dominate them.

Example:

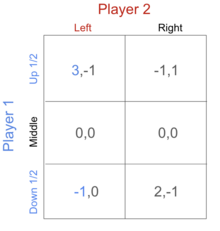
In this scenario, for player 1, there is no pure strategy that dominates another pure strategy. Let’s define the possibility of player 1 playing up as p, and let p = ½. We can set a mixed strategy where player 1 plays up and down at a possibility (½,½). When player 2 plays left, then the payoff for player 1 playing the mixed strategy of up and down is 1, when player 2 plays right, the payoff for player 1 playing the mixed strategy is 0.5. Thus regardless of whether player 2 chooses left or right, player 1 gets more from playing this mixed strategy between up and down than if the player were to play the middle strategy. In this case, we should eliminate the middle strategy for player 1 since it’s been dominated by the mixed strategy of playing up and down with probability (½,½).

See also

• Arbitrage
• Max-dominated strategy
• Newcomb's paradox
• Risk dominance
• Winning strategy

References

• Fudenberg, Drew; Tirole, Jean (1993). Game Theory. MIT Press.
• Gibbons, Robert (1992). Game Theory for Applied Economists. Princeton University Press. ISBN 0-691-00395-5.
• Gintis, Herbert (2000). Game Theory Evolving. Princeton University Press. ISBN 0-691-00943-0.
• Leyton-Brown, Kevin; Shoham, Yoav (2008). Essentials of Game Theory: A Concise, Multidisciplinary Introduction. San Rafael, CA: Morgan & Claypool Publishers. ISBN 978-1-59829-593-1.. An 88-page mathematical introduction; see Section 3.3. Free online at many universities.
• Rapoport, A. (1966). Two-Person Game Theory: The Essential Ideas. University of Michigan Press.
• 짐 라틀리프의 게임 이론 코스: 전략적 우위
• Shoham, Yoav; Leyton-Brown, Kevin (2009). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. New York: Cambridge University Press. ISBN 978-0-521-89943-7.. 계산적 관점에서 포괄적인 참조. 섹션 3.4.3, 4.5. 온라인 무료 다운로드.
• "혼합 전략에서의 엄격한 우위 – 게임 이론 101". gametheory101.com 2021-12-17 검색됨

이 글에는 크리에이티브 커먼스 귀속/공유 알리크 라이센스에 따라 라이센스가 부여된 PlanetMath에 대한 지배적 전략의 자료가 포함되어 있다.