괴델의 완전 정리
Gödel's completeness theorem괴델의 완전성 정리는 1차 논리학에서 의미적 진리와 통사적 검증 가능성 사이의 일치성을 확립하는 수학 논리의 기본 정리다.null
완전성 정리는 어떤 제1순서 이론에도 적용된다:T가 그러한 이론이고, φ은 문장(동일한 언어로 된)이고 T의 어떤 모델이 φ의 모델이라면, T의 문장을 공리로 사용하는 φ의 (일차적인) 증명서가 있다.사람들은 때때로 이것을 "진정한 것은 무엇이든 증명할 수 있다"라고 말한다.null
그것은 다른 모델에서 진실한 것을 다루는 모델 이론과 특히 공식적인 시스템에서 공식적으로 증명될 수 있는 것을 연구하는 증명 이론 사이에 긴밀한 연계를 만든다.null
그것은 1929년에 커트 괴델에 의해 처음 증명되었다.그 후 1947년 리언 헨킨이 박사 논문에서 입증의 어려운 부분을 '모델 존재 정리'로 제시할 수 있다고 관찰하면서 단순화되었다(49년 발표).헨킨의 증거는 1953년 기스베르트 하센재거에 의해 단순화되었다.null
예선
1차 논리에는 자연 공제의 시스템, 힐버트식 시스템 등 수많은 연역적 시스템이 있다.모든 연역체계에 공통적인 것은 형식적인 추리의 개념이다.이것은 특수하게 지정된 결론을 가진 공식의 순서(또는 경우에 따라서는 유한한 나무)이다.추론의 정의는 유한하며, 공식의 주어진 순서(또는 나무)가 실제로 추론이라는 것을 알고리즘적으로(예를 들어 컴퓨터로, 또는 손으로) 검증할 수 있는 것이다.null
1차 공식은 공식의 언어(즉, 공식의 변수에 값을 할당하는 경우)에 대한 모든 구조에서 사실이면 논리적으로 유효하다고 불린다.공식적으로, 그리고 나서 완전성 정리를 증명하기 위해서는 연역제도 또한 정의할 필요가 있다.모든 논리적으로 유효한 공식들이 어떤 형식적 추론의 결론이라면 연역체계를 완전체라고 하며, 특정 연역체계에 대한 완전정리는 이런 의미에서 완전체라는 정리다.따라서 어떤 의미에서 연역체계마다 다른 완성도 정리가 있다.완전성의 반대는 연역체계에서 논리적으로 유효한 공식만이 증명될 수 있다는 사실인 건전성이다.null
1차 논리학의 어떤 특정한 연역제도가 건전하고 완전하다면, 그것은 "완벽한" 것이다(논리적으로 타당하다면 그리고 논리적으로 타당할 경우에만 공식으로 증명할 수 있다), 따라서 같은 품질을 가진 다른 연역 시스템과 동등하다(한 시스템의 어떤 증명도 다른 것으로 변환할 수 있다).null
성명서
우리는 먼저 잘 알려진 동등한 시스템 중 하나를 선택하면서 1차 술어 미적분 연역 체계를 고친다.괴델의 원래 증거는 힐베르트-아커만 교정 시스템을 가정했다.null
괴델의 원래 공식화
완전성 정리는 공식이 논리적으로 타당하다면 공식에 대한 유한한 추론(공식증거)이 존재한다고 말한다.null
따라서 연역제는 모든 논리적으로 유효한 공식을 증명하기 위해 추가적인 추론 규칙이 필요하지 않다는 점에서 "완전"하다.완전성의 반대는 연역체계에서 논리적으로 유효한 공식만이 증명될 수 있다는 사실인 건전성이다.이 정리는 건전성(검증이 쉬운)과 함께 공식은 형식적 공제의 결론일 경우에만 논리적으로 유효하다는 것을 내포하고 있다.null
더 일반적인 형태
그 정리는 논리적인 결과의 관점에서 더 일반적으로 표현될 수 있다.우리는 문장 s가 연역 체계에서 T로부터 증명될 수 있는 경우 를 나타내는 이론 T의 통사적 결과라고 말한다우리는 s가 T의 모든 모델에 포함되는 T 로 표시된 T의 의미적 결과라고 말한다완성도 정리는 그 다음, 잘 정돈된 언어를 가진 어떤 1차 이론 T와 T의 언어로 된 어떤 문장 s에 대해서,
- T 그 다음에 T s s
컨버스(음향)도 포함되기 때문에, s {\displaystyle bdash s}이(가) s s인 에만 T }s T\에 따라 1차 논리에 대한 통사적 및 의미적 결과가 동일하다.null
이 보다 일반적인 정리는 예를 들어 임의의 집단을 고려하고 그 집단에 의해 문장이 충족됨을 보여줌으로써 집단이론의 공리로부터 증명할 수 있는 것으로 보여질 때 암묵적으로 사용된다.null
괴델의 원래 공식은 어떠한 공리 없이 이론의 특정한 경우를 취함으로써 추론된다.null
모델존재정리
완성도 정리도 헨킨의 모델 존재 정리의 결과로서 일관성 측면에서도 이해할 수 있다.우리는 이론 T가 우리의 연역 체계에서 s와 그것의 부정이 모두 T로부터 증명될 수 있는 문장이 없다면 구문론적으로 일관된다고 말한다.모델 존재 정리는 잘 정돈된 언어를 가진 어떤 1차 이론 T에 대해서도
- 이(가) 구문적으로 일치하면 T 에 모델이 있음.
뢰웬하임-스콜렘 정리와의 연관성이 있는 또 다른 버전은 다음과 같이 말한다.
- 모든 구문론적으로 일관되고 계수 가능한 1차 이론은 유한하거나 계수 가능한 모델을 가지고 있다.
헨킨의 정리를 감안할 때 완전성 정리는 다음과 같이 증명할 수 있다:t 헨킨의 정리의 모순에 의해 은 구문론적으로 일관성이 없다.따라서 모순({ )은 연역계통의 ∪ s로부터 증명할 수 있다.따라서( ) {\ {\displaystyle s 연역계통의 속성에 의해 s
산술의 정리로서
모델 존재 정리 및 그 증명서는 페아노 산술의 틀에서 공식화될 수 있다.정확히 말하면, 우리는 T의 각 기호를 기호의 인수가 되는 산술적 공식으로 해석함으로써 페아노 산술에서 일관적인 유효 1차 이론 T의 모델을 체계적으로 정의할 수 있다.(대부분의 경우, Peano 산술은 그 사실을 증명하지 못할 수도 있기 때문에, 우리는 공사의 가설로서 T가 일관된다고 가정할 필요가 있을 것이다.)그러나 이 공식에 의해 표현된 정의는 재귀적이지 않다(일반적으로 Δ이다2).null
결과들
완전성 정리의 중요한 결과는 이론의 공리로부터 가능한 모든 형식적 추론을 열거함으로써, 효과적인 1차 이론의 의미적 결과를 재귀적으로 열거할 수 있으며, 이를 이용하여 결론의 열거도 산출할 수 있다는 것이다.null
이는 특정 언어의 모든 구조에 대해 정량화하는 의미적 결과 개념의 직접적인 의미와 대조적으로 나타나는데, 이는 명백히 재귀적 정의가 아니다.null
또, 「제공성」의 개념, 즉 「테오렘」의 개념을, 즉, 그 이론의 공리의 선택된 시스템에 의존할 뿐, 증명 시스템의 선택에 의존하지 않는 명확한 개념으로 만든다.null
불완전성 이론과의 관계
괴델의 불완전성 이론은 수학에서 주어진 1차 이론 안에서 증명될 수 있는 것에 내재된 한계가 있다는 것을 보여준다.이름에서 "완전성"은 완전성의 또 다른 의미를 가리킨다(모델 이론 – 컴팩트함과 완전성 이론 사용). 의 언어로 된 모든 S }이(가) 입증 가능(⊢ S{\ T이거나 또는 검증 불가능( S인 경우 이론 complete(또는 decon(또는 decompleteprecompletionable)이 완성된다.null
첫 번째 불완전성 정리는 일관되고 효과적이며 로빈슨 Q")을 포함하는 T 이(가) 이러한 의미에서 불완전해야 한다고 명시하고 있는데, 이는 내에서 증명할 수도, 반증할 수도 없는 문장 T}을 명시적으로 구성함 Th.e 두 번째 불완전성 정리는 T 를 선택하여 T 자체의 일관성을 표현할 수 있음을 보여줌으로써 이 결과를 확장시킨다.null
는 에서 반증할 수 없으므로, 완전 정리는 S 가 거짓인 의 모델의 존재를 암시한다사실 는 π1 문장으로서, 즉 일부 미세한 성질은 모든 자연수에 대해 참이라고 명시하고 있으므로, 만일 그것이 거짓이라면, 어떤 자연수는 백과사전이다.만약 이 백색상이 자연수 내에 존재한다면, 그 존재는 T 에서 S {\를 반증할 것이다 그러나 불완전성 정리는 이것이 불가능함을 보여 주었으므로 백색수는 표준수가 아니어야 하며, 따라서 의 어떤 모델도 될 수 없다. 은(는) 거짓이며 비표준 숫자를 포함해야 한다.null
사실 산술적 모델 존재 정리의 체계적 구성에 의해 얻은 Q를 포함하는 어떤 이론의 모델은 항상 비균등적 검증성 술어와 그 자체의 구성을 해석하는 비균등적 방법으로 비표준적이므로 이 구성은 비반복적(재귀적 정의는 모호하지 않을 것이기 때문에)이다.null
또한 이 Q(예: 경계가 있는 실존 공식에 대한 유도를 포함하는 경우)보다 최소한 약간 더 강한 경우, 텐넨바움의 정리는 재귀적인 비표준 모델을 가지고 있지 않음을 보여준다.null
압축성 정리와의 관계
완전성 정리와 콤팩트성 정리는 일차 논리학의 두 가지 초석이다.이 두 가지 이론 모두 완전히 효과적인 방법으로 증명될 수는 없지만, 각각의 이론은 다른 이론으로부터 효과적으로 얻어질 수 있다.null
콤팩트성 정리는 공식 φ이 공식 γ의 (아마도 무한한) 집합의 논리적 결과라면, finite의 유한 부분 집합의 논리적 결과라고 말한다.이는 γ의 형식적 차감에서는 φ로부터의 공리의 유한한 수만이 언급될 수 있을 뿐이며, 이때 연역계통의 건전성은 φ이 유한한 집합의 논리적 결과임을 암시하기 때문이다.이 압축성 정리의 증명은 원래 괴델 때문이다.null
반대로, 많은 연역적 시스템의 경우, 콤팩트성 정리의 효과적인 결과로서 완전성 정리를 증명할 수 있다.null
완전성 정리의 비효과성은 역수학 계열을 따라 측정할 수 있다.셀 수 있는 언어에 대해 고려할 때, 완전성과 콤팩트성 이론은 서로 동등하고 약한 쾨니히의 보조정리라고 알려진 약한 형태의 선택과 동등하며, 동등성은 RCA에서0 증명할 수 있다(Peano 산술의 2차 변종, formulas01 공식에 대한 유도로 제한됨).약한 쾨니히의 보조마차는 선택의 공리 없이 제르멜로-프라엔켈 세트 이론의 체계인 ZF에서 증명할 수 있으며, 따라서 셀 수 있는 언어에 대한 완전성과 압축성 이론은 ZF에서 증명할 수 있다.그러나 그 이후로 언어가 임의로 큰 카디널리티의 경우 상황은 다르지만, 완전성과 콤팩트성 이론은 ZF에서 서로 확실히 동등하지만, 그것들은 또한 초필터 보조마라고 알려진 선택의 공리의 약한 형태와 동일할 수 있다.특히 ZF를 확장하는 어떤 이론도 같은 카디널리티의 집합에 있는 초필터 보조기 역시 증명하지 않고서는 임의의 (아마도 헤아릴 수 없는) 언어에 대한 완전성이나 콤팩트성 이론 중 하나를 증명할 수 없다.null
기타 로직의 완전성
완전성 정리는 모든 로직들을 보유하지 않는 1차 논리학의 중심 속성이다.예를 들어 2차 논리학에는 표준 의미론(Henkin 의미론에는 완전성 정리가 없지만 Henkin 의미론에는 완전성 속성을 가지고 있다)에 대한 완전성 정리가 없으며, 2차 논리학에서 논리적으로 검증된 공식들의 집합은 반복적으로 열거되지 않는다.모든 고차 로직도 마찬가지다.고차 로직의 경우 건전한 연역 시스템을 만들 수 있지만, 그러한 시스템은 완성될 수 없다.null
린드스트룀의 정리는 1차적 논리가 콤팩트함과 완전성을 모두 만족시키는 가장 강력한(특정 제약조건에 따른) 논리라고 기술하고 있다.null
크립케 의미론에 관한 모달논리학이나 직관논리에 대해 완전성 정리가 증명될 수 있다.null
교정쇄
괴델의 원래 정리 증명은 문제를 특정 구문형식의 공식에 대한 특수한 경우로 축소시킨 다음, 이 양식을 임시변통으로 처리하는 것으로 진행되었다.null
현대 논리 문헌에서 괴델의 완전성 정리는 괴델의 원래 증명보다는 헨킨의 증명으로 보통 증명된다.헨킨의 증거는 어떤 일관된 1차 이론에 대한 용어 모델을 직접 구성한다.제임스 마겟슨(2004)은 이사벨 정리 프로베러를 이용해 컴퓨터화된 형식적 증거를 개발했다.[1]다른 증거들도 알려져 있다.null
참고 항목
추가 읽기
- Gödel, K (1929). "Über die Vollständigkeit des Logikkalküls". Doctoral dissertation. University Of Vienna.
{{cite journal}}: cite 저널은 (도움) 완전성 정리의 첫 번째 증거를 요구한다. - Gödel, K (1930). "Die Vollständigkeit der Axiome des logischen Funktionenkalküls". Monatshefte für Mathematik (in German). 37 (1): 349–360. doi:10.1007/BF01696781. JFM 56.0046.04. S2CID 123343522. 논문과 동일한 자료로, 보다 간결한 설명과 장문의 서론을 생략한다.
- ^ James Margetson (Sep 2004). Proving the Completeness Theorem within Isabelle/HOL (PDF) (Technical Report).
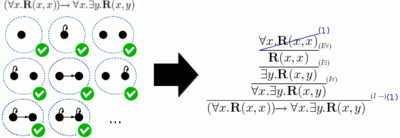


 (가) 구문적으로 일치하면 T
(가) 구문적으로 일치하면 T 








