위상 초상화

단순한 진자의 잠재적 에너지 및 위상 초상화. x축은 각도가 되어 2㎛ 라디안마다 자체로 감싼다는 점에 유의한다.

단순한 진자의 움직임을 위해 위상 초상화가 어떻게 구성되는지를 예시한다.

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

2

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

t

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

+

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

2

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

-

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

)

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

+ y

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

=

{\frac {d^{2}y}{dt^{2}}}+\mu (y^{2}-1){\frac {dy}{dt}}+y=0

{\dystyle {\frac

{

d^{2}y}{dt^{2}}}}+\mu(y^{2}-1){\frac {

d}{dy

}{d}{

d}+

y=0

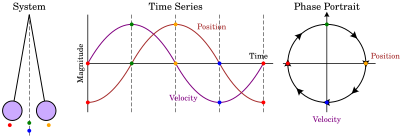
위상 초상화는 위상 평면에서 역동적인 시스템의 궤적을 기하학적으로 표현한 것이다. 초기 조건의 각 집합은 다른 곡선 또는 점으로 표현된다.

위상 초상화는 역동적인 시스템을 연구하는 데 귀중한 도구다. 그들은 주공간의 전형적인 궤도를 그린 그림으로 구성되어 있다. 이는 선택된 매개변수 값에 대해 유인기, 리피터 또는 한계 사이클이 있는지와 같은 정보를 나타낸다. 위상적 등가성의 개념은 서로 다른 두 단계의 초상화가 동일한 질적 동적 행동을 나타내는 시기를 명시함으로써 시스템의 행동을 분류하는 데 중요하다. 유인원은 "싱크"라고도 불리는 안정된 지점이다. 리펠러는 불안정한 점으로 간주되는데, 이를 '출처'라고도 한다.

동적 시스템의 위상 초상화 그래프는 시스템의 궤적(화살로 표시)과 안정 상태(점 포함) 및 상태 공간의 불안정한 안정 상태(원 포함)를 나타낸다. 축은 상태 변수의 것이다.

예

단순한 진자, 그림(오른쪽)을 보라.
위상 초상화가 고정점인 원점을 중심으로 타원으로 구성된 단순 고조파 오실레이터.
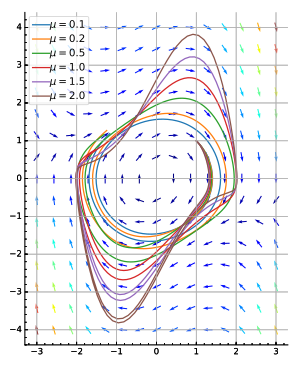
Van der Pol 오실레이터 그림 보기(오른쪽 아래)
파라미터 평면(c-plane) 및 Mandelbrot 세트

일반 미분방정식의 동작 시각화

위상 초상화는 일반적인 미분방정식(oDE)의 계통의 방향성을 나타낸다. 위상 초상화는 시스템의 안정성을 나타낼 수 있다. ^[1]

안정성^[1]

불안정한	대부분의 시스템 솔루션은 시간이 지남에 따라 ∞을 지향하는 경향이 있다.
점증상 안정적	모든 시스템 솔루션은 시간이 지남에 따라 0이 되는 경향이 있음
중성적으로 안정적	시스템 솔루션 중 어느 것도 시간이 지남에 따라 ∞을 지향하지 않지만, 대부분의 솔루션도 0을 지향하지 않는다.

ODE 시스템의 위상 초상 거동은 시스템의 고유값 또는 추적 및 결정인자(추적 = λ₁ + λ₂, 결정인자 = λ₁ x λ₂)에 의해 결정될 수 있다.^[1]

위상 초상화^[1] 동작

고유값, 추적, 결정 요인	위상 세로 모양
λ₁ & λ은₂ 실제와 반대 기호가 있다. 결정인자 < 0	안장(불안정)
λ₁ & are은₂ 진짜고 같은 부호의 것이고₁ λ₂ ;; 0 < 결정인자 < (trace² / 4)	노드(추적 < 0일 경우 안정화 가능, 트레이스 > 0일 경우 불안정)
λ₁ & λ은₂ 실제 및 가상 구성요소를 모두 가지고 있다. (1998² / 4) < 결정인자	Spiral(추적 < 0일 경우 안정화 가능, 트레이스 > 0일 경우 불안정)

참고 항목

참조

^ ^a ^b ^c ^d 헤인즈 밀러, 아서 마턱 18.03 미분 방정식 2010년 봄. 매사추세츠 공과대학교: MIT OpenCourseWare, https://ocw.mit.edu. 라이센스: Creative Commons BY-NC-SA (Haynes Miller의 보조 노트 26: https://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_26.pdf)

Jordan, D. W.; Smith, P. (2007). Nonlinear Ordinary Differential Equations (fourth ed.). Oxford University Press. ISBN 978-0-19-920824-1. 제1장.
Steven Strogatz (2001). Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering. ISBN 9780738204536.

외부 링크

선형 위상 초상화, MIT 산술집.

[:0-1] 헤인즈 밀러, 아서 마턱 18.03 미분 방정식 2010년 봄. 매사추세츠 공과대학교: MIT OpenCourseWare, https://ocw.mit.edu. 라이센스: Creative Commons BY-NC-SA (Haynes Miller의 보조 노트 26: https://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_26.pdf)

[1]

Search

위상 초상화

네임스페이스

더

목차

예

일반 미분방정식의 동작 시각화

참고 항목

참조

외부 링크