크로스 프로덕트

수학에서 교차곱 또는 벡터곱(가끔 그 기하학적 중요성을 강조하기 위해 지시된 영역곱)은 3차원 지향 유클리드 벡터 공간$($서 E {\$displaystyle$ E$})$의 두 벡터에 대한 이항 연산이며 기호$$× {$displaystyle \times$로 나타난다.두 개의 선형 ind가 주어지면ependent 벡터 a와 b, 교차곱 a × b ("a cross b"로 읽음)는 a와 ^[1]b 모두에 수직인 벡터이며, 따라서 이들을 포함하는 평면에 수직이다.그것은 수학, 물리학, 공학, 컴퓨터 프로그래밍에 많은 응용 분야를 가지고 있다.도트 제품(투영 제품)과 혼동해서는 안 됩니다.

두 벡터가 방향이 같거나 서로 완전히 반대 방향(즉, 선형 독립적이지 않음)이거나 둘 중 하나의 길이가 0이면 교차곱은 ^[2]0이 됩니다.보다 일반적으로 곱의 크기는 변에 대한 벡터가 있는 평행사변형의 면적과 같다. 특히, 두 수직 벡터의 곱의 크기는 길이의 곱이다.

교차곱은 반교합적(즉, a × b = - b × a)이며, 덧셈에 대한 분포(즉, a × (b + c) = a × b + a × c)^[1]이다.$공간{\displaystyle }$ E$(\displaystyle$ E$)$와 교차곱은 가환도 관계도 없는 실수 대수로, 교차곱이 Lie 괄호인 Lie 대수로 되어 있습니다.

점곱과 마찬가지로, 그것은 유클리드 공간의 메트릭에 따라 달라지지만, 점곱과 달리, 그것은 또한 공간의 방향(또는 "손잡이")의 선택에 달려있다.교차곱과 관련하여 벡터의 외부곱은 임의의 치수(쌍방향자 또는 2형식 결과)로 사용할 수 있으며 공간의 방향과는 무관하다.

이 곱은 기존의 3차원 교차곱과 마찬가지로 방향과 미터법을 이용하여 n차원에서는 n-1 벡터의 곱을 취하여 모든 벡터에 수직인 벡터를 생성할 수 있다.그러나 제품이 벡터 결과를 가진 단순하지 않은 바이너리 제품으로 제한되는 경우, 3차원 ^[3]및 7차원으로만 존재합니다.그러나 7차원의 교차곱은 바람직하지 않은 특성을^[which?] 가지고 있기 때문에 수학물리학에서는 ^[4]다차원 시공간과 같은 양을 나타내기 위해 사용되지 않는다.(기타 치수에 대해서는 § Generalizations, 이하를 참조해 주세요).

정의.

두 벡터 a와 b의 교차곱은 3차원 공간에서만 정의되며 a × b로 표시됩니다.물리학과 응용 수학에서는 쐐기 표기법 a b b가 종종 사용된다(이름 벡터 ^[5][6][7]곱과 함께). 그러나 순수 수학에서는 이러한 표기법은 보통 벡터 곱의 n차원 추상화인 외부 곱만을 위해 예약된다.

교차곱 a × b는 a와 b 모두에 수직(직교)인 벡터 c로 정의되며, 오른쪽 규칙에^[1] 의해 주어진 방향과 벡터가 가로지르는 ^[2]평행 사변형의 면적과 크기가 같다.

교차곱은 다음 공식으로^[8][9] 정의됩니다.

$\displaystyle \mathbf {a} \times \mathbf {b} = \left\left\\mathbf {b} \right\sin(\theta)\\mathbf {n} }$

여기서:

• θ는 이들을 포함하는 평면에서 a와 b 사이의 각도이다(단, 0°에서 180° 사이).
• 'a'와 'b'는 벡터 a와 b의 크기이다.
• n은 a와 b를 포함하는 평면에 수직인 단위 벡터이며, 오른쪽 규칙에서 주어진 방향(정렬)^[2]이다.

상기 식에 의해 벡터 a와 b가 평행(즉, 이들 사이의 각도θ가 0° 또는 180°)일 경우 a와 b의 교차곱은 제로 벡터 0이다.

방향

관례상 벡터 n의 방향은 오른손 검지를 a의 방향으로, 가운데 손가락을 b의 방향으로만 가리키는 오른손 규칙으로 주어진다.다음으로 벡터 n이 엄지손가락에서 나옵니다(인접 그림 참조).이 규칙을 사용하는 것은 교차곱이 반교환적이라는 것을 의미한다. 즉, b × a = -(a × b)이다.집게손가락으로 먼저 b를 가리키고 가운데손가락으로 a를 가리키면 엄지손가락이 반대방향으로 힘을 주어 곱 벡터의 부호를 반전시킨다.

교차곱 연산자는 공간의 방향(위의 정의에서 명시적)에 의존하므로, 두 벡터의 교차곱은 "참" 벡터가 아니라 의사벡터이다.자세한 내용은 § 핸드니스 참조.

이름

1881년, 조시아 윌러드 깁스와 올리버 헤비사이드는 각각 마침표(a. b)와 "x"(a x b)를 사용하여 점곱과 교차곱을 ^[10]둘 다 소개했다.

1877년, 도트곱의 결과는 스칼라이고 교차곱의 결과는 벡터라는 사실을 강조하기 위해 윌리엄 킹든 클리포드는 ^[10]두 연산을 위한 대체적인 이름인 스칼라곱과 벡터곱을 만들었다.이러한 대체 명칭들은 여전히 문헌에서 널리 사용되고 있다.

교차 표기법(a × b)과 교차 곱은 모두 a × b의 각 스칼라 성분이 a와 b의 비대응 성분을 곱하여 계산된다는 사실에서 영감을 받았을 수 있다.반대로 도트곱 a δ b는 a와 b의 대응하는 성분 간의 곱셈을 포함한다.아래에 설명된 바와 같이, 교차곱은 특수 3 × 3 행렬의 행렬식의 형태로 표현될 수 있다.사루스의 규칙에 따르면, 이것은 교차 대각선으로 식별되는 행렬 요소 간의 곱셈을 포함합니다.

컴퓨팅

좌표 표기법

만약 (i, j,k)가 양의 방향의 직교 정규 기저라면, 기저 벡터는 다음과 같은 등식을^[1] 만족한다.

${\displaystyle{\begin{alignedat}{2}\mathbf{\color{ 푸른}{나는}}&\times{\color{ 빨간}{j}}및 \mathbf,&=\mathbf{\color{녹색}{k}}\\\mathbf{\color{ 빨간}{j}}&\times{\color{녹색}{k}}및 \mathbf,&=\mathbf{\color{ 푸른}{나는}}\\\mathbf{\color{녹색}{k}}&\times{\color{ 푸른}{나는}}및 \mathbf,&=\mathbf{\color{ 빨간}{j}.}\end{alignedat}}}$

이는 교차 곱의 반상환성에 의해 다음과 같은 의미를 갖는다.

${\displaystyle{\begin{alignedat}{2}\mathbf{\color{ 빨간}{j}}&\times{\color{ 푸른}{나는}}및 \mathbf,&=-\mathbf{\color{녹색}{k}}\\\mathbf{\color{녹색}{k}}&\times{\color{ 빨간}{j}}및 \mathbf,&=-\mathbf{\color{ 푸른}{나는}}\\\mathbf{\color{ 푸른}{나는}}&\times{\color{녹색}{k}}및 \mathbf,&=-\mathbf{\color{ 빨간}.{j}}\end{alignedat}}}$

교차 곱의 반상환성(및 선형 독립성의 명백한 결여)은 또한 다음을 의미한다.

$i$× ${\displaystyle i\mathbf{}}$ ${\displaystyle =}$ ${\displaystyle j\mathbf{}=k\mathbf{}}$ × ${\displaystyle k\mathbf{}}$ ${\displaystyle =}$ \$displaystyle \mathbf {blue}$ {i} \$times$ \mathbf {color {blue} {$i} =$ \$mathbf {color$ {$red}$ {$j}$ \times $\mathbf$ {$k}$ {$green}$ \mathbf {color$}$

이러한 등식은 교차곱의 분포도와 선형성과 함께 (위 정의에서 쉽게 따르지 않지만) 두 벡터 a와 b의 교차곱을 결정하기에 충분하다.각 벡터는 표준 기저 벡터에 평행한 세 가지 직교 성분의 합으로 정의할 수 있습니다.

$({displaystyle {color {blue} {i}} &+a_{2} \mathbf {color {red} {j} &+a_{3})}\mathbf {color {green} {k} \\mathbf {b} &=b_{1} \mathbf {blue} {i} &&+b_{2} \mathbf {color {red} {j} &+b_{3}\mathbf {color {green} {k} \end {alignedat} }$

이들의 교차곱 a × b는 분포도를 사용하여 확장할 수 있다.

${\displaystyle\mathbf {a} \times \mathbf {b} = {}&(a_{1}\mathbf {blue} {i}} +a_{2}\mathbf {red} {j} +a_{3}}\mathbf {green}{k}\times (b_{1}\mathbf {blue}{i}} +b_{2}\mathbf {red} {j} +b_{3}}\mathbf}{\color{녹색}{k})\\={}&, a_ᆯb_ᆰ(\mathbf{\color{}일 경우 파란 색{나는}}\mathbf{\color{}일 경우 파란 색{나는}}\times)+a_ᆱb_ᆲ(\mathbf{\color{}일 경우 파란 색{나는}}\mathbf{\color{}일 경우 빨간{j}}\times)+a_ᆳb_ᆴ(\mathbf{\color{}일 경우 파란 색{나는}}\mathbf{\color{}녹색{k}}\times)+{}\\&, a_ᆶb_ᆷ(\mathbf{\color{}일 경우 빨간{j}}\mathbf{\color{}일 경우 파란 색{나는}}\times)+a_{2}b._{2}(\maThbf{\color{ 빨간}{j}};a_ᆲb_ᆳ(\mathbf{\color{}녹색{k}}\mathbf{\color{}일 경우 파란 색{나는}}\times)+a_ᆴb_ᆵ(\mathbf{\color{}녹색{k}}\mathbf{\color{}일 경우 빨간{j}}\times)+a_{3}b_{3}(\mathbf{\color{녹색}{k}}\mathbf{\colo \times\mathbf{\color{ 빨간}{j}})+a_ᆯb_ᆰ(\mathbf{\color{}일 경우 빨간{j}}\mathbf{\color{}녹색{k}}\times)+{}\\& \times.r{green}{k}}\\end{aligned}}$

이는 a × b가 i, j 또는 k로 정렬된 벡터를 포함하는 9개의 단순한 교차 곱의 합으로 분해되는 것으로 해석될 수 있다.이들 9개의 교차곱 각각은 서로 평행하거나 직교하기 때문에 다루기 쉬운 2개의 벡터로 동작합니다.이 분해로부터, 상기의 등식을 사용하고, 유사한 용어를 수집함으로써, 다음을 얻는다.

${\displaystyle{\begin{정렬}\mathbf{를}\times, \quad)a_{1}b_{1}\mathbf{0}+a_{1}b_{2}\mathbf{\color{녹색}{k}}-a_{1}b_{3}\mathbf{\color{ 빨간}{j}}\\&, -a_{2}b_{1}\mathbf{\color{녹색}{k}}{0}+a_{2}b_{3}\mathbf{\color{ 푸른}{나는}}\\& +a_{2}b_{2}\mathbf, +a_{3}b_{1}\mathbf{\color{ 빨간}{j}})-a_{3}b_{2}\mathbf{년{b}={}& \mathbf.색{ 파란}{i} \ +a_{3}b_{3}\mathbf {0} \\={}&(a_{2}b_{3}-a_{3}b_{2}\mathbf {blue}{i}} +(a_{3}b_{1}-a_{3}b_{2}) +(a_{1}-{1}b_f {color {color {color {{2}) {color {{} {} {color {{color} {color {color} {color}}}}$

즉, 결과 벡터 s = si₁ + sj₂ + sk₃ = a × b의 세 가지 스칼라 성분이

${{displaystyle}s_{1}&=a_{2}b_{3}-a_{2}b_{2}&=a_{3}b_{1}-a_{3}b_{3}\=a_{1}b_{2}-{2}-{1}b_{1}-{1}-{1}-{1}-{1}-{1}-{1}-{1}-{b_{1}-{1}-{b_{1}-{1}-{1}-{1}-{1}-{b_{1}-{1}-{1}-{1}-{1}-{b_aligned}-{1}$

열 벡터를 사용하여 다음과 같은 결과를 나타낼 수 있습니다.

${\displaystyle {bmatrix}s_{1}\\s_{3}\end{bmatrix}=barget{bmatrix}a_{2}b_{3}-a_{3}b_{2}\a_{3}b_{1}b_{1}\b_1}b_{1}\b_{1}\b_1}$

행렬 표기법

교차곱은 공식 ^{[note 1][1]}행렬식으로도 표현될 수 있다.

${\displaystyle \mathbf {a\times b} = syslog {vmatrix}\mathbf {j} &\mathbf {k} \a_{1}&b_{2}&b_{3}\end{vmatrix}$

이 행렬식은 Sarrus 법칙 또는 보조 요인 확장을 사용하여 계산할 수 있습니다.사루스의 법칙을 이용하여, 그것은 확장되어

${\displaystyle {displaystyle}\mathbf {a\times b} &=(a_{2}b_{3}b_{1}\mathbf {j} +a_{1}b_{k}-(a_{3}b_{2}\mathb_i}+mathb_i}$

대신 첫 번째 행을 따라 보조 요인 확장을 사용하면 다음과 같이 확장됩니다^[11].

${\displaystyle{\begin{정렬}\mathbf{a\times b}&={\begin{vmatrix}a_{2}&, a_{3}\\b_{2}&, b_{3}\end{vmatrix}}{나는}-{\begin{vmatrix}a_{1}& \mathbf, a_{3}\\b_{1}&, b_{3}\end{vmatrix}}{j}+{\begin{vmatrix}a_{1}& \mathbf, a_{2}\\b_{1}&, b_{2}\end{vmatrix}}{k}\\& \mathbf, =(a_{2}b_{3}-a_{3}b_{2})\mathbf{나는}-(a_{1}b_{3}-a_{3}b_{1})\m.athbf{j}+(a_{1}b_{2}-a_{2}b_{1})\mathbf {k},\end {aligned}}$

결과 벡터의 구성 요소를 직접 제공합니다.

Levi-Civita 텐서 사용

• 어떤 기초에서도 $교차곱{\displaystyle }$a × $(표시$ 스타일 a$\$$times$ b$)$는 $텐셔너리식{\displaystyle {}_{}}$ $E_ijk}a^{i}b$$^{j}($${\displaystyle {여기}_{}}$서 $E_ijk}$는 공변 Levi-Civita 텐서)에 의해 주어진다.그것은 여기에 제시된 내적 공식에 해당된다.
• a${\displaystyle }$× $(표시 스타일$ a$\times$ b$)$는 공간과 같은 방향의 직교 기준에서 의사 텐셔너리식 ${\displaystyle {}_{}{}^{}}$ a$ib$ j(표시 $스타일$ \$varepsilon _{i}a^{i}b$$^{$j$$})에 의해 주어진다.$여기$서 ${\displaystyle {\mathrm{\theta i}}_{}}$ k$(표시$ 스타일 \$varepsilon _ijita$})는$$ Levi-기호이다.이것은 일상적인 물리학에 사용되는 공식이지만, 이 특별한 기초 선택에만 적용됩니다.
• 어떤 직교 기준에서든${\displaystyle a}$ ×$$b {\$displaystyle$$$a$\times$ b$}$는 의사 요인식${\displaystyle (-1{}^{}}$ ${\displaystyle B^{}}$ ${\displaystyle i_{}}$ ${\displaystyle {\mathrm{ij}}_{}}$ k ${\displaystyle a^{}}$ i ${\displaystyle b^{}}$j {$1}$ \ $varepsilon$ _${ijk} a^{i}$ b$^{j$$\},{\displaystyle {여기}^{}}$서${\displaystyle {}^{}}$(-1${\displaystyle )}$ B $=$ ± ${\displaystyle 1}$ {$pm\b}이다.$

후자의 공식은 우리가 직교기저를 역방향으로 할 때 공간의 방향을 바꿀 필요가 없다.

특성.

기하학적 의미

교차 곱의 크기는 a와 b를 변으로 하는 평행 사변형의 양의 영역으로 해석할 수 있다(그림 1 참조).^[1]

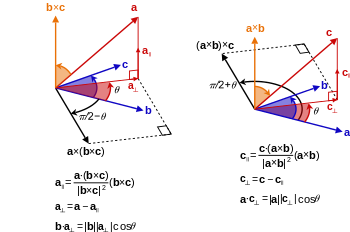
실제로, 교차곱과 스칼라 삼중곱(scalar triple product)이라고 불리는 점곱의 조합을 사용하여 a, b 및 c를 모서리로 하는 평행 입방체의 부피 V를 계산할 수도 있다(그림 2 참조).

$\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} \cdot )=\mathbf {c} \cdot (\mathbf {a} \times \mathbf {b})}$

스칼라 삼중곱의 결과는 음수일 수 있으므로, 평행입방체의 부피는 절대값에 의해 주어진다.

$\displaystyle V= \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ).}$

교차곱의 크기는 인수 사이의 각도의 사인(sine)에 의해 결정되기 때문에 교차곱은 점곱이 평행성의 척도인 것과 같은 방식으로 수직성의 척도라고 생각할 수 있습니다.두 단위 벡터가 주어졌을 때, 두 단위 벡터가 수직이면 크기가 1이고 두 단위 벡터가 평행하면 크기가 0입니다.두 단위 벡터의 점곱은 정반대로 작용합니다. 단위 벡터가 수직일 경우 0이고 단위 벡터가 평행일 경우 1입니다.

단위 벡터는 두 가지 편리한 식별을 가능하게 합니다. 두 단위 벡터의 점곱은 두 단위 벡터 사이의 각도의 코사인(양수 또는 음수일 수 있음)을 생성합니다.두 단위 벡터의 교차 곱의 크기는 사인(항상 양수)을 산출합니다.

대수적 성질

두 벡터의 교차곱이 제로 벡터(즉, a × b = 0)이면 입력 중 하나 또는 둘 다 제로 벡터(a = 0 또는 b = 0)이거나 평행 또는 역평행(a ≤ b)이므로 둘 사이의 각도의 사인값이 0(θ = 0° 또는 θ = 180° 및 sin = 0)이 됩니다.

벡터의 자기 교차곱은 제로 벡터입니다.

$\displaystyle \mathbf {a} \times \mathbf {a} = \mathbf {0} .}$

교차곱은 반교합적입니다.

$\displaystyle \mathbf {a} \times \mathbf {b} =-(\mathbf {b} \times \mathbf {a} ),$

분배와 덧셈,

$\displaystyle \mathbf {a} \times (\mathbf {b} + \mathbf {c} )=(\mathbf {a} \times \mathbf {c} ) + (\mathbf {a} \times \mathbf {c} ) ,$

스칼라 곱셈과 호환되므로

$\displaystyle(r,\mathbf {a})\times \mathbf {b}=r,(\mathbf {a} \times \mathbf {b})}$

연관성은 없지만 야코비 정체성을 충족합니다.

$\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} \times \mathbf {a} +\mathbf {c} \times \times \mathbf {bf {b}) = mathbf {c}.$

분포성, 선형성 및 자코비 항등식은 R 벡터 공간이 벡터³ 덧셈 및 교차곱과 함께 3차원에서의 실제 직교 그룹의 Lie 대수인 SO(3)를 형성한다는 것을 보여준다.교차곱은 취소 법칙을 따르지 않는다. 즉, a × b = a × c가 θ 0인 것은 b = c를 의미하는 것이 아니라 다음 사항을 의미한다.

$\displaystyle {displaystyle {mathbf {0} &=(\mathbf {a} \times \mathbf {c} )-\&=\mathbf {a} \times (\mathbf {b} -\mathbf {c})\\\end {aligned}}$

이는 b와 c가 취소되는 경우일 수 있지만 a와 b - c가 평행한 경우일 수 있습니다. 즉, 이들은 스케일 계수 t에 의해 관련되므로 다음과 같은 결과가 초래됩니다.

${\displaystyle \mathbf {c} =\mathbf {b} +t,\mathbf {a} ,}$

스칼라 t를 위해서요

위와 같이 a × b = a × c 및 a 0 0에 더하여 a b b = a c c인 경우

$(\displaystyle {displaystyle {mathbf {a} \times (\mathbf {b} - \mathbf {c} )=\mathbf {a} \cdot (\mathbf {b} - \mathbf {c} )&=0,\end {aligned})$

b - c는 a에 대해 평행(교차곱이 0인 경우)과 수직(도트곱이 0인 경우)을 동시에 가질 수 없으므로 b와 c가 소거되는 경우 b = c이어야 한다.

기하학적 정의에서 교차곱은 a × b에 의해 정의된 축에 대한 적절한 회전 하에서 불변한다.공식:

${\displaystyle (}$ ${\displaystyle R\mathbf{}}$a${\displaystyle }$)${\displaystyle }$× ( ${\displaystyle R\mathbf{}}$b ) ${\displaystyle =R}$ (${\displaystyle a\mathbf{}}$ ×${\displaystyle b\mathbf{}}$) \ $displaystyle ( R$\ $mathbf { a }$ ) \$times$ \ $mathbf { b$}$$$=$ $R$$$( \ $displaystyle$$$${\displaystyle \mathrm{R<img\; alt="R"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/4b0bfb3769bf24d80e15374dc37b0441e2616e33"\; style="vertical-align:\; -0.338ex;\; width:1.764ex;\; height:2.176ex;">}}$)$=$$$1 \ $det$ style

보다 일반적으로, 교차곱은 행렬 변환에서 다음과 같은 동일성을 따릅니다.

$\displaystyle (M\mathbf {a} )\times (M\det M)\left (M^{-1}\right)^{\mathrm {T} }(\mathbf {b})=\operatorname {cof} M(\mathb} \times {a} \mathb} \times$

$여기$서$$M {\$displaystyle$ M$}$은 3x3 매트릭스이고$,$ ${\displaystyle {{(}^{}}^{\mathrm{}}}$- 1) T {{$displaystyle \left$(M$^{-1}\$right$)^{\mathrm${$T}}}$는 역행렬의 전치이며, ${displaystyle \operatorname$ {cof$}$은 보조 행렬입니다.M$(\displaystyle$ M$)$이$$ 회전 매트릭스일 $경우{\displaystyle }$ 이 공식이 전자의 공식으로 어떻게 환원되는지를 쉽게 알 수 있다.M$${\$displaystyle$ M$}$이(가) 일반 $×$b ${\displaystyle \mathbf$ {a} \$times$\mathbf {$b}$에 적용되는 3x3 대칭 행렬인 $경우{\displaystyle }$ 다음 관계가 성립합니다.

$\displaystyle M(\mathbf {a} \times \mathbf {b} )=\operatorname {Tr}(M)(\mathbf {a} \times M\mathbf {b} +\mathbf {b} \times M\mathbf {a})$

두 벡터의 교차곱은 벡터를 행으로 하는 2 × 3 행렬의 늘 공간에 있습니다.

$\displaystyle \mathbf {a} \times \mathbf {b} \in NS\left ({\begin{bmatrix}\mathbf {a} \\\mathbf {b} \end{bmatrix}}}\right).}$

두 교차 곱의 합계에 대해 다음 식별 정보가 유지됩니다.

$\displaystyle \mathbf {a} \times \mathbf {b} +\mathbf {c} \times \mathbf {a} -\mathbf {c} =(\mathbf {b} -\mathbf {d}) \times \mathbf {a} +\c}$

차별화

미분 미적분의 곱 법칙은 모든 쌍선형 연산에 적용되며, 따라서 교차 곱에도 적용됩니다.

${\displaystyle {d}{dt}(\mathbf {a} \times \mathbf {a} } {dt} =times \mathbf {b} +\mathbf {a} \times \frac {d\mathbf {b} } }$

여기서 a와 b는 실수 변수 t에 의존하는 벡터이다.

3배의 제품 확장

크로스 곱은 트리플 곱의 두 가지 형태에 모두 사용됩니다.세 벡터의 스칼라 삼중곱은 다음과 같이 정의된다.

$\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} ) }$

이는 엣지 a, b 및 c로 연결된 의 부호화된 볼륨이며, 따라서 벡터는 위의 순서에서 균등하게 배열된 순서로 사용할 수 있습니다.따라서 다음 사항이 동일합니다.

$\displaystyle \mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} \cdot (\mathbf {c} \times \mathbf {a} ) =\mathbf {cdot (\mathbf {a} \times \mathbf {b} ) ) )$

벡터 삼중곱은 벡터의 다른 교차곱의 결과와 교차곱이며, 다음 공식에 의해 도트곱과 관련된다.

$\displaystyle {displaystyle \mathbf {a} \times \mathbf {c} \mathbf {b} = \mathbf {c} \mathbf {c} - \mathbf {a} \mathbf {c} \times$

니모닉 "BAC - CAB"는 오른쪽 멤버의 벡터 순서를 기억하기 위해 사용됩니다.이 공식은 벡터 계산을 단순화하기 위해 물리학에서 사용됩니다.기울기와 벡터 미적분에 유용한 특별한 경우는,

$(\displaystyle \displaystyle \times \mathbf {f})&=\displayla (\displayla \cdot \mathbf {f})-(\displaystyle \cdot \mathbf {f})-(\displaystyla \cdot \mathbf {f {f} {f})\displayla \times \times \cdot \times \cdot \mathbf {f {f})$

여기서 ²θ는 벡터 라플라시안 연산자입니다.

다른 정체성은 교차곱과 스칼라 삼중곱을 관련짓는다.

$(\displaystyle {mathbf {a} \times \mathbf {b} \times \mathbf {c} \cdot (\mathbf {b} \times \mathbf {c}) \mathbf {a} \times \mathbf {a} \times)\timesI-\mathbf {c} \mathbf {a} ^{\mathrm {T} }\right)\mathbf {d} \\=(\mathbf {a} \cdot \mathbf {c}),\mathbf {d}-(\mathbf {d} \mathbot {cd})$

여기서 I는 아이덴티티 매트릭스입니다.

대체 제제

교차곱과 도트곱은 다음과 같이 관련되어 있습니다.

$\displaystyle \left \mathbf {a} \times \mathbf {b} \right \^{2} \left \mathbf {b} - \cdot \mathbf {b} {b} - (\mathbf {b})^2} =\left \ mathbf {a} 。$

오른쪽은 벡터들에 의해 정의된 평행사변형 영역의 제곱인 a와 b의 그램 행렬식이다.이 조건은 교차곱의 크기를 결정합니다.즉, 도트 곱은 다음과 같이 정의되므로 두 벡터 사이의 각도 θ의 관점에서 다음과 같이 정의된다.

$\displaystyle \mathbf {a\cdot b} =\left\mathbf {a} \right\mathbf {b} \right\cos \theta,}$

위의 관계를 다음과 같이 다시 작성할 수 있습니다.

$\displaystyle \left \mathbf {a\times b} \right\^{2}=\left\mathbf {a} \right\^{2}\left(1-\cos ^{2}\theta \right).}$

피타고라스 삼각함수 항등식을 호출하면 다음과 같이 얻을 수 있습니다.

$\displaystyle \left \mathbf {a} \times \mathbf {b} \right \left \mathbf {a} \right \ \mathbf {b} \right \ sin \theta \right }$

이는 θ 단위로 표현되는 교차곱의 크기로, a와 b에 의해 정의된 평행사변형의 면적과 같다(위 정의 참조).

이 요구사항과 교차곱이 성분 a와 b와 직교한다는 특성과의 조합은 교차곱의 ^[13]대체 정의를 제공한다.

라그랑주 항등식

관계:

$\displaystyle \left \mathbf {a} \times \mathbf {b} \right \ ^2} \equiv \det \det {bmatrix} \mathbf {a} \cdot \mathbf {a} \cdot \mathbf {a} \cdot \mathbf {a}$

오른쪽과 관련된 다른 관계, 즉 다음과 ^[14]같이 표현된 라그랑주의 정체성과 비교할 수 있다.

$\displaystyle \sum _{1\leq i<j\leq n}\left(a_{i}-a_{j}b_{i}\right)^2}\equiv \left\\\mathbf {a}\right\\mathbf {b}\right\{2-{bcda}^2-{bcda}^2-{bcd}$

여기서 a와 b는 n차원 벡터일 수 있다.이것은 또한 표면에 대한 리만 부피 형태가 벡터 미적분의 표면 요소임을 보여준다.n = 3인 경우, 이 두 방정식을 결합하면 ^[15]성분 측면에서 교차곱의 크기에 대한 식이다.

$\displaystyle {displaystyle \mathbf {a} \times \mathbf {b} \right \ ^{2} \equiv \sum _ {1\leq i } \left ( a _ { i } b _ { j } - a _ { j } b _ { i } \ \ right } \ \ equiv { 1 }$

동일한 결과는 다음과 같은 교차 곱의 구성 요소를 사용하여 직접 확인할 수 있습니다.

$(\displaystyle \mathbf {a} \times \mathbf {b} \equiv \det {\hat {mathbf {i} }} & {\hat {mathbf {j} } } } } } } \a_{1}&a_{b}}$

R에서³, 라그랑주 방정식은 4분위 대수에서 노름의 승수 vw = v w의 특별한 경우이다.

이것은 비네-코시 항등식의 ^[16][17]3차원 경우인 라그랑주 항등식이라고도 불리는 또 다른 공식의 특별한 경우이다.

$\displaystyle (\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \equiv (\mathbf {a} \cdot \mathbf {c} )-(\mathbf {d} \mathbf {d} \mathbf {cd} \mathbf {cd})\cdot}$

a = c 및 b = d이면 위의 공식으로 단순화됩니다.

무한소 회전 생성기

교차곱은 R의 회전³ 발생기를 매우 쉽게 기술합니다.구체적으로, n이 R의³ 단위 벡터이고 R(θ, n)이 각도 θ(n의 끝에서 보았을 때 반시계방향으로 측정됨)로 n에 의해 지정된 원점을 통과하는 축 주위의 회전을 나타낸다면,

$(\displaystyle\왼쪽).{d \over d\phi }\right _{\phi =0}R(\phi,{\boldsymbol {n}){\boldsymbol {x}}=boldsymbol {n}\times {x}}}$

R의 모든³ 벡터 x에 대해.따라서 n을 갖는 교차곱은 n에 대한 회전의 극소량 발생기를 나타냅니다.이러한 무한소 생성기는 회전군 SO(3)의 Lie 대수를 형성하고 교차곱을 갖는 Lie 대수³ R이 Lie 대수와 동형이라는 결과를 얻는다.

다른 계산 방법

행렬 곱셈으로 변환

벡터 교차곱은 스큐-대칭 행렬과 벡터의 ^[16]곱으로도 표현될 수 있습니다.

여기서 supercript는 전치 연산을 나타내며 [a]_×는 다음과 같이 정의됩니다.

벡터 a에 대한 스큐-대칭 행렬의 열 [a]_×,i은 단위 벡터를 사용하여 교차곱을 계산하여 얻을 수도 있습니다.그것은,

또는여기서 ${\$ { $displaystyle \otimes }$는 외부 제품 오퍼레이터입니다.

또한 a 자체가 교차곱으로 표현되는 경우:

그리고나서

이 결과는 기하학적 대수를 사용하여 더 높은 차원으로 일반화할 수 있습니다.특히 어떤 차원에서도 스큐대칭행렬로 동정할 수 있기 때문에 스큐대칭행렬과 벡터 사이의 곱은 쌍대칭행렬과 ^[18]벡터 곱의 1등급 부분과 동등하다.3차원에서 바이벡터는 벡터에 대해 이중이므로 곱은 벡터 대신 바이벡터를 사용하여 교차곱과 동등합니다.더 높은 차원에서도 곱은 여전히 계산될 수 있지만 바이벡터는 더 많은 자유도를 가지며 ^[18]벡터와 동등하지 않습니다.

이 표기법은 예를 들어 에피폴라 기하학에서 훨씬 더 쉽게 사용할 수 있습니다.

교차곱의 일반적인 특성으로부터 다음과 같이 즉시 이어진다.

그리고.그리고 [a]_×가 비뚤어진다는 사실로 미루어 보아 다음과 같다.

위의 트리플 프로덕트 확장(bac-cab 규칙)은 이 표기법을 사용하여 쉽게 입증할 수 있습니다.

이상과 같이, 교차곱을 갖는 리 대수³ R은 리 대수와 동형이며, 그 원소는 3×3 스큐 대칭 행렬로 동정할 수 있다.a → [a]_× 지도는 R과 so(3) 사이의³ 동형성을 제공한다.이 지도에서 3 벡터의 교차곱은 3x3 스큐-대칭 행렬의 정류자에 해당합니다.

표준 기저 벡터를 사용하는 교차곱 행렬 변환

${\displaystyle {}_{}{\mathbf{}}^{}}$ R ${\displaystyle {\mathrm{}}^{}}$× ${\displaystyle 1^{}}$$$({$displaystyle \mathbf {e} _{i}\in \mathbf {R}$^{$3\$$times1})$로 나타내며, 일반 $벡터{\displaystyle \mathbf{}}$ ${\displaystyle {\mathrm{}}^{}}$$i$ R 3$$× 1$$ ({$displaystyle \mathbf {v}$\$in \mathbf {3})$의 교차곱인$$i {i} - 정규 기저 벡터를 나타낸다.iven by:${\displaystyle }v{\displaystyle \mathbf{}}$ × ${\displaystyle {}_{}}$ i ${\displaystyle {}_{}}$ ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}\mathbf{}}$\ $displaystyle$\ $mathbf${ $v }$ \$times$ \ $mathbf${$e } _${ i$$= \ $mathbf$ { C$}$_ { i } \ $mathbf$ { $v$ , 여기서 $${\displaystyle \mathbf {C} _{1}=param {bmatrix} 0&0&1\\0&1&1\end {bmatrix},\param \mathbf {C}_{2}=param {bmatrix} 0&1&0&0&0\end$$ 이러한 매트릭스는 다음 속성을 공유합니다. ${\displaystyle {}_{}^{}}$ T $=$ - ${\displaystyle {}_{}}${\$displaystyle \mathbf {C} _{i}^{\textrm$ {T}}=-\$mathbf {C} _{$i}}$$ (csw-displaystyle$);$ 트레이스와 행렬식은 모두 제로입니다. ${\displaystyle {\mathbf{}}_{}}$( ${\displaystyle {}_{}}$) ${\displaystyle =}$ ${\displaystyle 2}${ $style${$text${ rank } （ $mathbf${ $C$} _ { i } $= 2$; ${\displaystyle {}_{}{\mathbf{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ T ${\displaystyle {=}_{}^{}}$ ${\displaystyle {\mathbf{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$ { $displaystyle \mathbf { C$ }$_$ { $i$} \ $mathbf${ $C$} $_${ $i } =$ \ $mathbf${ $P$} _ { \ $mathbf${ $e } =$ { i } ^{ \ $perp }$ （$$ ） ; $벡터{\displaystyle \mathbf{}}$ v${\displaystyle 0\mathbf{}}$ 0$(\$ \$neq \mathbf {0})$의 직교 투영 행렬은 P ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {=}_{}{}^{}v\mathbf{}}$ ( ${\displaystyle {v{\mathbf{}}^{}}^{}}$ ${\displaystyle {{}^{}{v}^{}\mathbf{}}^{}}$) - ${\displaystyle {}^{}}$ {\$displaystyle \mathbf {P} _{\mathbf {v} =$ \$left(textbf {$0})로 주어진다.직교 보수는 ${\displaystyle {\mathbf{}}_{}^{}}$ v $=$ ${\displaystyle I\mathbf{}}$- ${\displaystyle {\mathbf{}}_{}}$ v$$\$displaystyle \mathbf {P} {{\mathbf {v}} {{\perp}}=\mathbf$ {I} $-$$\$mathbf {$P}} {\$mathbf {$V$$\}\}\}\}\}$에 의해 주어지며$,$ $여기$서 $I$는 \displaystyle \$mathbf${I$$$}$ 행렬이다$.$v $=$ ${\displaystyle {}_{}}$\$displaystyle \mathbf {v}$ =\$mathbf {e}$ _${i$의 특수한 경우, 다음을 확인할 수 있다. $${\displaystyle \mathbf{P}_{\mathbf{e}_{1}}^{^{\perp}}={\begin{bmatrix}0&, 0&, 0\\0&, 1&, 0\\0&, 0&, 1\end{bmatrix}},\quad\mathbf{P}_{\mathbf{e}_{2}}^{^{\perp}}={\begin{bmatrix}1&, 0&, 0\\0&, 0&, 0\\0&, 0&, 1\end{bmatrix}},\quad\mathbf{P}_{\mathbf{e}_{3}}^{^{\perp}}={\begin{bmatrix}1&, 0&, 0\\0&, 1&amp을 말한다.0\\0&, 0&, 0\end{bmatrix}}}$$ 직교 투영 행렬의 다른 속성은 투영(선형 대수)을 참조하십시오.

텐서의 지수 표기법

교차곱은 Levi-Civita 텐서_ijk E 및 도트곱 θ의^mi 관점에서 정의할 수 있으며, 이는 텐서 적용을 위한 벡터 표기법 변환에 유용하다.

$\displaystyle \mathbf {c} =\mathbf {a\times b} \왼쪽 화살표 \c^{m}=\sum _{i=1}^{3}\sum _{k=1}^3}\eta ^{mi}E_{ijk}a^{j}b^{k}$

여기서 $인덱스{\displaystyle }$ i${\displaystyle ,}$ ${\displaystyle j,}$ $(\style$ i$,j,k)$는 벡터 성분에 해당합니다.교차곱의 이러한 특성은 종종 아인슈타인 합산 규칙을 사용하여 보다 간결하게 표현됩니다.

$\displaystyle \mathbf {c} =\mathbf {a\times b} \왼쪽 화살표 \c^{m}=\eta ^{mi}E_{ijk}a^{j}b^{k}$

1부터 3까지의 값에 대해 반복 지수가 합산됩니다.

긍정 지향의 직교 정규 기저에서 η^mimi = ( （ Kronecker 델타 ） $e{\displaystyle {}_{}}$ e ${\displaystyle e_{}}$ $=$ ${\displaystyle {\epsilon }_{}}$ i ${\displaystyle j_{}}$ ${\displaystyle k_{}}$（ $display style$ E_${ijk$ } =\$varepsilon$ _${ijk}$ $$（ Levi-Civita 기호).이 경우, 이 표현은 교차곱의 스큐-대칭 표현의 또 다른 형태이다.

${\displaystyle [\varepsilon _{ijk}a^{j}]=[\mathbf {a}_{\times }}$

고전역학에서: Levi-Civita 기호를 사용하여 교차곱을 표현하는 것은 물리적 시스템이 등방성일 때 기계적 대칭을 명백하게 만들 수 있습니다. (예: 3차원 공간에서 자유롭게 진동하는 후크의 법칙에 있는 입자를 고려합니다; 이 차원들 중 어느 것도 어떤 의미에서도 "특별하지 않습니다" 그래서 대칭입니다.s는 위에서 언급한 Levi-Civita ^{[citation needed]}표현에 의해 명확해진 교차 제품 표현 각운동량에 있다.

니모닉

"xyzzy"라는 단어는 교차곱의 정의를 기억하기 위해 사용될 수 있습니다.

한다면

$\displaystyle \mathbf {a} = \mathbf {b} \times \mathbf {c} }$

여기서:

${\displaystyle \mathbf {a} =param {bmatrix} a_{x} \\a_{y} \\a_{z}\end{bmatrix}, \mathbf {b} =param {bmatrix} b_{x}\b} \b_{x} \mathbc} \mathbf} \matrix} \mathbf=\c$

그 후, 다음과 같이 합니다.

$\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}$

$\displaystyle a_{y}=b_{z}c_{x}-b_{x}c_{z}$

${\displaystyle a_{z}=b_{x}c_{y}-b_{y}c_{x}.}$

두 번째와 세 번째 방정식은 첨자 x → y → z → x를 수직으로 회전시켜 첫 번째 방정식에서 얻을 수 있습니다.물론 문제는 첫 번째 방정식을 기억하는 방법이고, 이 목적을 위해 두 가지 옵션을 사용할 수 있습니다. Sarrus 스킴의 관련된 두 대각선(i를 포함하는 대각선)을 기억하는 방법 또는 xyzzy 시퀀스를 기억하는 방법입니다.

Sarrus 스킴의 첫 번째 대각선은 위에서 언급한 3×3 행렬의 주요 대각선이기 때문에, xyzzy라는 단어의 첫 세 글자는 매우 쉽게 기억될 수 있다.

크로스 비주얼라이즈

위의 니모닉 디바이스와 마찬가지로 방정식의 두 벡터 사이에 "크로스" 또는 X를 시각화할 수 있습니다.이는 올바른 교차 곱 공식 기억에 도움이 될 수 있습니다.

한다면

$\displaystyle \mathbf {a} = \mathbf {b} \times \mathbf {c} }$

그 후, 다음과 같이 합니다.

${\displaystyle \mathbf {a} = syslog{bmatrix} b_{x}\\b_{y}\end{bmatrix}\times {bmatrix}c_{x}\c_{y}\c_{z}\end{bmatrix}.}$

x$(\$의 공식을 얻으려면 공식에서 ${\displaystyle b_{}}$x(\$displaystyle b_{x})$와 c $(\$})를$$ 삭제하고 다음 2개의 컴포넌트를 제거합니다.

$({displaystyle a_{x}=sys {bmatrix}b_{y}\end {bmatrix}\times {bmatrix}c_{y}\c_{z}\end {bmatrix}).}$

$(\$에 대해 이 작업을 수행할 경우, 다음 두 요소는 z 구성요소 뒤에 x 구성요소가 오도록 매트릭스를 "감겨야" 합니다.알기 쉽게 하기 위해 y$(\$에 대해 이 작업을 수행할 때 다음 2개의 구성 요소는 z와 x(순서대로)여야 합니다.$(\$의 $경우{\displaystyle {}_{}}$ 다음 두 가지 구성요소는 x와 y로 간주해야 합니다.

$({displaystyle a_{y}=param {bmatrix}b_{z}\end {bmatrix}\times {bmatrix}\c_{x}\end {bmatrix},\a_{z}=param {bmatrix}b_{x}\times}\times$

x$(\$의 $경우{\displaystyle {}_{}}$ 왼쪽 요소에서 오른쪽 요소를 가리키는 것으로 교차 연산자를 시각화하면 왼쪽의 첫 번째 요소에 오른쪽 행렬에서 십자선이 가리키는 요소를 곱할 수 있습니다.다음으로 왼쪽 아래쪽에 있는 원소에 십자선이 가리키는 원소를 곱한 값을 뺍니다.$그{\displaystyle {}_{}}$ 결과 x$(\$의 ${\displaystyle {공식}_{}}$입니다.

${\displaystyle a_{x}=b_{y}c_{z}-b_{z}c_{y}.}$

y$(\$와 z$(\$도 같은 방법으로 관련 공식을 구성할 수 있습니다.

적용들

크로스 제품에는 다양한 컨텍스트의 응용 프로그램이 있습니다.예를 들어, 컴퓨터 기하학, 물리학 및 공학에서 사용됩니다.다음은 철저한 예가 아닌 목록입니다.

계산기하학

교차곱은 3차원 공간에서 두 개의 스큐 선(같은 평면에 있지 않은 선) 사이의 거리를 계산하는 데 나타납니다.

교차곱은 컴퓨터 그래픽스에서 자주 수행되는 연산인 삼각형 또는 다각형에 대한 법선을 계산하는 데 사용할 수 있습니다.예를 들어 폴리곤 내의 한 점에 대한 폴리곤(시계방향 또는 시계반대방향)의 감기는 폴리곤(휠을 찌르는 것과 같은)을 삼각측량하고 교차곱을 사용하여 (스포크 사이의) 각도를 가산하여 각 각도의 부호를 추적함으로써 계산할 수 있다.

평면의 계산기하학에서 교차곱은 $3개$의 $p$ ${\displaystyle {}_{}}$${\displaystyle {}_{}}$ (${\displaystyle {}_{}{x\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$y${\displaystyle {}_{}}$ ), ${\displaystyle {}_{}}$2${\displaystyle }$= (${\displaystyle {}_{}{x\mathrm{}}_{}}$ 2,$2$) ({1}= $(x_{1$}),$p_${2}= ($x_{2},y_{$2$$}) ${\displaystyle {및\mathrm{}}_{}}$ ${\displaystyle {x\mathrm{}}_{}{}_{}}$3 (${\displaystyle {}_{}}$$)$에 의해 정의된 예각의 부호를 결정하는 데 ${\displaystyle {}_{}}$된다.$({\displaystyle {}_{}{}_{}}$1, ${\displaystyle {p\mathrm{}}_{}}$2 $)({displaystyle (p_{1},p_{2})}$${\displaystyle }$및$$ (${\displaystyle {p\mathrm{}}_{}}$1 , $)({displaystyle (p_{1},p_{3}))$의 2쌍에 의해 정의된 2개의 코플러너 벡터의 교차곱의 방향(아래쪽 또는 아래쪽)에 스펀드를 바꿉니다$.$예각의 부호는 그 표현의 부호이다.

$({displaystyle P=(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1}),}$

두 벡터의 교차곱의 부호 길이입니다.

"오른쪽" 좌표계에서 결과가 0이면 점이 공선이고, 양수이면 3개의 ${\displaystyle {점}_{}}$이 p 2$({$ $p_{2}})$에서$$p 3$({$p_${$3$\}\})$까지의 p$$ $주위$의 정회전각을 구성하고, 그렇지 않으면 음의 각도를 구성합니다.다른 관점에서 $보면{\displaystyle }$ P$({displaystyle$ P$$$})$의 ${\displaystyle {부호}_{}}$는$p3$({$displaystyle p_${3$})$의${\displaystyle {}_{}{왼쪽}_{}}$인지${\displaystyle {}_{}}$p2$.({displaystyle p_1}, p_{2})$의 $오른쪽$인지 알 수 있습니다.$}$

교차곱은 사면체 또는 평행입방체와 같은 다면체의 부피를 계산하는 데 사용됩니다.

각운동량 및 토크

주어진 원점에 대한 입자의 각운동량 L은 다음과 같이 정의된다.

$\displaystyle \mathbf {L} = \mathbf {r} \times \mathbf {p} ,}$

여기서 r은 원점에 대한 입자의 위치 벡터이고 p는 입자의 선형 운동량입니다.

마찬가지로 점 A 주위의 점 B에 가해지는 힘_B F의 모멘트 M은 다음과 같이 주어진다.

$\displaystyle \mathbf {M} _{\mathrm {A} =\mathbf {r} _{\mathrm {AB} } \times \mathbf {F} _{\mathrm {B} },}$

역학에서는 힘의 모멘트를 토크라고도 하며$written{\displaystyle }$ {\$displaystyle \mathbf \tau }$로 표기합니다.

위치 r, 선형 운동량 p 및 힘 F는 모두 참 벡터이므로 각 운동량 L과 힘 M의 모멘트는 모두 의사 벡터 또는 축 벡터이다.

강체

교차곱은 강성 모션에 대한 설명에 자주 나타납니다.강체 위의 두 점 P와 Q는 다음과 같이 관련될 수 있습니다.

$\displaystyle \mathbf {v} _{P} - \mathbf {v} _{Q} = \times \left(\mathbf {r} _{P} - \mathbf {r} _{Q} \right} )$

$여기$서$$r$(\displaystyle \mathbf${r$})$은 점의 $,$ $v(\displaystyle \mathbf$ {v$})$는 속도,$${\(\$displaystyle\boldsymbol\mega}}}}$는 신체의 각 속도입니다.

$위치{\displaystyle \mathbf{}}$r(\$displaystyle \mathbf {r})$ 및$$ $속도{\displaystyle \mathbf{}}$v(\$displaystyle \mathbf {v})$는 참 벡터이므로 각속도$\theta {\displaystyle \mathit{}}$(\$displaystyle\boldsymbol\mega}}})$는 의사벡터 또는 축 벡터입니다.

로렌츠력

교차곱은 이동 전하_e q에 의해 발생하는 로렌츠 힘을 설명하는 데 사용됩니다.

$\displaystyle \mathbf {F} =q_{e}\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)}$

속도 v, 힘 F 및 전계 E는 모두 참벡터이므로 자기장 B는 의사벡터이다.

다른.

벡터 미적분학에서 교차곱은 벡터 연산자 컬의 공식을 정의하기 위해 사용된다.

행렬 곱셈의 관점에서 교차곱을 다시 쓰는 방법은 특히 일치하는 구속조건을 도출할 때 에피폴라 및 멀티뷰 지오메트리에 자주 나타납니다.

외부 제품으로서

교차곱은 외부곱으로 정의할 수 있습니다.3차원 ^[19]이외의 외부 제품으로 일반화할 수 있습니다.이^[which?] 뷰를 통해 교차곱을 자연스럽게 기하학적으로 해석할 수 있습니다.외부 대수학에서 두 벡터의 외부 곱은 쌍방향 벡터이다.바이벡터는 방향성 평면 요소이며, 벡터가 방향성 선 요소인 것과 거의 같은 방식으로 이루어집니다.2개의 벡터 a와 b가 주어졌을 때, 쌍방향 벡터 a δ b를 a와 b에 걸친 배향 평행사변형이라고 볼 수 있다.그런 다음 바이벡터 a µ b의 호지별을 취하여 2-벡터를 벡터에 매핑하여 교차곱을 구한다.

$(*displaystyle a\times b=\star (a\times b),}$

이것은 지향성 다차원 요소가 바이벡터에 "수직"이라고 생각할 수 있습니다.예를 들어, 4차원에서 바이벡터의 호지 듀얼은 2차원 바이벡터인 반면, 3차원에서만 지향성 1차원 요소가 됩니다.따라서 3차원에서만 a와 b의 벡터 교차곱을 바이벡터 a b b에 대해 쌍대 벡터로 정의할 수 있다.이 벡터는 쌍대 벡터에 대해 수직이며, 방향은 좌표계의 핸드니스에 따라 달라지며, 단위 법선 벡터에 대해 a b b가 단위 bector에 대해 갖는 것과 같은 크기를 가진다.정확히 적절한 값이다.상기의 넥타이

손재주

이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2021년 9월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍 확인)

일관성.

물리 법칙이 방정식으로 쓰여질 때, 핸드니스 등 좌표계를 임의로 선택할 수 있습니다.고려해야 할 모든 변환에서 양쪽이 동등하게 동작하지 않는 방정식을 결코 적지 않도록 주의해야 한다.예를 들어 방정식의 한 변이 두 극 벡터의 교차곱인 경우 결과가 축 벡터임을 고려해야 합니다.따라서 일관성을 위해 반대쪽도 축 ^{[citation needed]}벡터여야 합니다.보다 일반적으로 교차곱의 결과는 피연산자(극 벡터 또는 축 벡터)의 종류에 따라 극 벡터 또는 축 벡터 중 하나가 될 수 있다.즉, 극 벡터와 축 벡터는 교차곱을 적용하면 다음과 같은 방식으로 상호 연관된다.

• 극벡터 × 극벡터 = 축방향 벡터
• 축 벡터 × 축 벡터 = 축 벡터
• 극 벡터 × 축 벡터 = 극 벡터
• 축방향 벡터 × 극방향 벡터 = 극방향 벡터

또는 상징적으로

• 극성 × 극성 = 축방향
• 축 × 축 = 축
• 극 × 축 = 극성
• 축방향 × 극방향 = 극방향

교차곱은 극벡터일 수도 있기 때문에 거울상 변환으로 방향을 바꾸지 않을 수도 있습니다.위의 관계에 따라 피연산자 중 하나가 극 벡터이고 다른 하나가 축 벡터(예를 들어 두 극 벡터의 교차곱)인 경우 이러한 현상이 발생합니다.예를 들어 3개의 극 벡터를 포함하는 벡터 삼중곱은 극 벡터이다.

외부 대수를 사용하여 핸드니스 없는 접근이 가능하다.

직교 정규 기법의 역설

(i, j,k)를 직교 정규 기저로 한다.벡터 i, j, k는 공간의 방향에 의존하지 않는다.방향성이 없는 경우에도 정의할 수 있습니다.따라서 축 벡터가 될 수 없습니다.그러나 i와 j가 극 벡터라면 k는 i × j = k 또는 j × i = k에 대한 축 벡터이다.이것은 역설이다.

"축"과 "극성"은 물리적 벡터, 즉 속도 또는 자기장과 같은 물리적 양을 나타내는 벡터입니다.벡터 i, j 및 k는 수학적 벡터이며 축방향도 극방향도 아닙니다.수학에서, 두 벡터의 교차곱은 벡터이다.모순은 없다.

일반화

교차곱을 더 높은 차원으로 일반화하는 방법은 여러 가지가 있습니다.

리 대수

교차곱은 가장 단순한 Lie 곱 중 하나로 볼 수 있으며, 따라서 다선형성, 스큐-대칭성, 야코비 항등식의 공리를 만족시키는 이항곱으로 공리화된 리 대수에 의해 일반화된다.많은 리 대수가 존재하며, 그들의 연구는 리 이론이라고 불리는 수학의 주요 분야이다.

예를 들어 하이젠베르크 대수는 ${\displaystyle {\mathrm{}}^{}}$ $3$에${\displaystyle {}^{}}$또 다른 Li 대수 구조를 $제공$합니다$.$ {{displaystyle${\displaystyle }$\$mathbf${R$}^{$$3},${$displaystyle$\{x$,y,z\}}$의 곱은 [$=$ [$,z]$이다${\displaystyle \mathrm{.}}$

쿼터니온스

교차곱은 4분의 1로도 설명할 수 있다.일반적으로 벡터 [a₁, a₂, a₃]를 사분위₁ ai₂ + aj₃ + ak로 표현하면 2개의 벡터의 곱을 사분위수로 하여 그 결과의 실부를 삭제함으로써 2개의 벡터의 교차곱을 얻을 수 있다.실제 부분은 두 벡터의 점곱의 음수가 될 것이다.

옥토니언

4분위 대신에 옥토니언을 이용하는 것과 같은 방법으로 7차원 벡터의 크로스곱을 얻을 수 있다.다른 차원에서는 두 벡터의 중요하지 않은 벡터 값 교차곱이 존재하지 않는 것은 규격화된 분할 대수가 1, 2, 4, 8 차원을 가진 유일한 대수라는 후르비츠의 정리의 결과와 관련이 있다.

외장 제품

일반적으로 벡터를 생성하는 바이너리 크로스 곱의 직접적인 유사점은 없습니다.그러나 두 벡터의 외부 곱이 일반 벡터가 아닌 2-벡터라는 것 외에는 유사한 성질을 가진 외부 곱이 있습니다.위에서 설명한 바와 같이, 교차곱은 Hodge star 연산자를 사용하여 2-벡터를 벡터에 매핑함으로써 3차원 외부곱으로 해석할 수 있다.외부 제품의 Hodge 듀얼은 (n - 2) 벡터를 생성하며, 이는 임의의 차원에서의 교차곱의 자연스러운 일반화입니다.

외부 곱과 도트 곱은 합계를 통해 결합되어 기하학적 대수학에서 기하학적 곱을 형성할 수 있습니다.

외부 제품

위에서 말한 바와 같이, 크로스 곱은 외부 제품의 Hodge 듀얼로 입체적으로 해석할 수 있습니다.임의의 유한 n차원에서 n - 1 벡터의 외부 곱의 호지 쌍대는 벡터이다.따라서 이항 연산 대신 임의의 유한 차원에서는 교차곱이 주어진 n - 1 벡터의 외부곱의 호지 쌍으로 일반화된다.이러한 일반화를 외부 ^[20]제품이라고 합니다.

정류자 제품

대수의 3차원 벡터 공간을 3차원 기하학 대수의 2차원 부분 대수로 해석하는 것(1-수직이 아님), $여기$서 ${\displaystyle i{\mathbf{}}_{}}$ ${\displaystyle =}$ ${\displaystyle {}_{}{\mathbf{}}_{}}$ ${\displaystyle {2\mathbf{}}_{}}$e 3 \$displaystyle$ \mathbf {$i} =$ \$mathbf {e_{2}$} \$mathbf${$e_${$3{\displaystyle \mathbf{}}$}$$$=$ = $3$ e ${\displaystyle {3\mathbf{}}_{}}$ \$mathbf$ style {$mathbf$$}$$$, $및{\displaystyle \mathbf{}}$ ${\displaystyle k{\mathbf{}}_{}}$ ${\displaystyle =}$ ${\displaystyle {}_{}{\mathbf{}}_{}}$ ${\displaystyle {1\mathbf{}}_{}}$ e$$2 { $style \mathbf {k$} = \$mathbf {e_{1} \mathbf {e_{2}}$ $\},$ 기하학 대수의 정류자 곱에 정확히 해당하며, 두 개의$$기호$$× {\$displaystyle \times$ $\}$을 사용합니다. 정류자 곱은 $2-DISPLAYLE$ A$$및 $A$에 대해 $정의$됩니다.기하학 대수의 $스타일$ B$}$는 $다음$과 같습니다.

$({displaystyle A\times B=bgtfrac {1}{2}}(AB-BA)})$

${\displaystyle \mathrm{여기}}$서 A B$(\displaystyle$ AB$)$는 기하학적 ^[21]곱입니다.

정류자 곱은 3차원의 임의의 다변환자로 일반화될 수 있으며, 이는 등급 1(1-벡터/참 벡터) 및 등급 2(2-벡터/의사 벡터)의 요소만으로 구성된 다변환자가 된다.2개의 1-벡터의 정류자 곱은 실제로 외부 곱과 동일하고 2-벡터를 생성하는 반면, 1-벡터와 2-벡터의 정류자는 기하학 대수에서 좌우 수축에 대응하는 진정한 벡터를 생성한다.두 개의 2-벡터의 정류자 곱은 대응하는 곱이 없기 때문에 처음부터 2-벡터에 대해 정류자 곱이 정의됩니다.또한 3개의 2-벡터의 정류자 삼중곱은 벡터 대수에서 동일한 3개의 의사벡터의 벡터 삼중곱과 동일하다.그러나 기하학 대수에서 세 개의 1-벡터의 정류자 삼중곱은 벡터 대수에서 동일한 세 개의 참 벡터의 벡터 삼중곱의 음수이다.

고차원에 대한 일반화는 고차원 기하학적 대수에서 2-벡터의 동일한 정류자 곱에 의해 제공되지만, 2-벡터는 더 이상 의사 벡터가 아니다.3차원 2벡터의 정류자 곱/교차곱이 가장 단순한 리 대수에 대응하듯이, 정류자 곱을 갖춘 고차원 기하학 대수의 2벡터 서브 대수도 리 ^[22]대수에 대응한다.또한 3차원에서와 마찬가지로 정류자 곱은 임의의 다중 벡터로 더욱 일반화될 수 있다.

다선형 대수

다선형 대수의 맥락에서 교차곱은 지수를 상승시킴으로써 3차원 체적 ^{[note 2]}형태인 (0,3)-텐서로부터 얻은 (1,2)-텐서(혼합 텐서, 구체적으로는 쌍선형 맵)로 볼 수 있다.

구체적으로는, 3차원 부피 형태에서는, 이 3개의 벡터에 의해서 주어지는 행렬의 행렬식을 취해, 곱${\displaystyle }V{\displaystyle }$ ×${\displaystyle }$V × ${\displaystyle V}$ ${\displaystyle \to }$ $,$ {$style$ V$\times$ V$\times$ V\$to\$mathbf {$R},}$를 정의한다.이중성에 의해, 이는 $함수{\displaystyle V}$ × ${\displaystyle {}^{}}$ ${\displaystyle \to }$ V${\displaystyle {}^{}}$δ$,$ {\$displaystyle$$V\times$V\$to$ V$^{*}}($임의의 두 입력은 세 번째 입력에 대한 평가를 $통해{\displaystyle }$ ${\displaystyle 함수\mathbf{}}$ V$$ R ~ \$mathbf {R}$를 부여함) 및 내부 제품(일반적으로 닷 제품 등)의 존재에 상당한다.동형사 $V{\displaystyle }$ ${\displaystyle \to }$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ , ${\displaystyle$ V$\to$ V$^{*}}$ 이므로$$ 맵${\displaystyle }V{\displaystyle }$ × $,$ {\$displaystyle$V\$times$V\$to$ V$,}$ 이 생성됩니다. a (0,3)-1992 (3 벡터 입력, 스칼라 출력)가 입력(1,2).

위의 대수를 기하학으로 변환하면, $함수{\displaystyle }$ ${\displaystyle V\mathbf{}}$ $→$ R \$displaystyle V\$to \$mathbf${R$\}$를 ${\displaystyle \mathrm{정의}}$하는 함수 ${\displaystyle "(a,}$ b${\displaystyle }$, -${\displaystyle }$)${\displaystyle }${$displaystyle (a$, b ,$$- )$$}" (처음 두 벡터가 고정되고 마지막 벡터가 입력)에 의해 정의된 평행입체의 부피"는 도트 곱으로 고유하게 표현될 수 있다.이 벡터는 $교차곱{\displaystyle }$a ×${\displaystyle b}$입니다$.$ {\$displaystyle$ a$\times$ b$.}$ 이$$ 관점에서 교차곱은 스칼라 삼중곱 ${\displaystyle \mathrm{V}}$ ${\displaystyle o}$l (${\displaystyle a}$ ,${\displaystyle b}$ ,${\displaystyle c}$ )$=$ (${\displaystyle a}$ ×${\displaystyle b}$ )${\displaystyle .}$ c$$. \ $displaystyle \mathrm {Vol$} ($a$ ,$b$ )= ( a \ $times$b ) $cdot$ c$$} 로 정의됩니다.

마찬가지로 고차원에서는 ($)\displaystyle(0,n)-$tensor인$$ n차원 체적 형태의 지수를 높여 일반화 교차곱을 정의할 수 있다.교차곱의 가장 직접적인 일반화는 다음 중 하나를 정의하는 것입니다.

• $a{\displaystyle }$${\displaystyle }$( ${\displaystyle 1}$,${\displaystyle }$n -${\displaystyle 1}$ $){$ $displaystyle ( 1$, $n-1$) - exters$$${\displaystyle }$。${\displaystyle \mathrm{입력}}$n -$$1 { $displaystyle$( $n$-$$) -${\displaystyle }$ary$$ 벡터 값 곱 또는 출력 1 벡터입니다.
• a${\displaystyle }$(${\displaystyle n}$ -${\displaystyle 2}$ ,${\displaystyle 2}$ )$${$displaystyle$( n -$2$) } -displaystyle$$ ( n - 2 ) -displaystyle ( n - 2 ) -displaystyle ( n - 2 ) -displaystyle ( n - 2 ） - rank n - 2의 출력 스큐-disputer tensor ( n - 2의 스큐 텐서)$다른$ k에${\displaystyle \mathrm{대해}}$( ${\displaystyle k}$,$$n - k ) {$displaystyle$($k$, n - k$$ ) - tensors 를${\displaystyle }$정의할 수도 있습니다.

이러한 곱은 모두 다선형 및 스큐 대칭이며, 행렬식 및 패리티의 관점에서 정의할 수 있습니다.

$({\displaystyle n}$ -${\displaystyle 1}$ )$${ $displaystyle$( n -$1$$$) - ary$$$$ 곱은 $다음$과 같이 설명할 수 있습니다${\displaystyle .}$ ${\displaystyle {}_{}}$ -$$ { $displaystyle$v _ { 1 }${\displaystyle {}^{}}$ $v{\displaystyle {}_{}{1\mathrm{}}_{}}$,${\displaystyle }$… , $v$- 1 { $displaystyle v_{$1} \$$$displaystyle$\$mathbf {R}$^ { $n$$$} ^ { n$$$$} }$$} n$$ n n n v v v v v v ${\displaystyle {}_{}}$ v ${\displaystyle {}_{}}$ { { { { { product their their their${\displaystyle {}_{}}$their their product product product product ${\displaystyle {product\mathrm{}}_{}}$$ystyle v_{n}=v_{1}\times \cdots$\times $v_{n-1}:$ 다음과$$ 같습니다.

• ${\displaystyle {vi}_{}}$,$${\$displaystyle v_${i$}$에 의해 정의된 하이퍼플레인에 수직입니다.
• magnitude는 $,$ {\$displaystyle$$$v_${$$i$}에 의해$$ 정의된 병렬동위원소의 부피입니다. 이 ${\displaystyle {부피}_{}}$는$vi$, {\displaystyle $v_${$}$의 그램 행렬식으로 계산할 수 있습니다.
• ${\displaystyle {v1\mathrm{}}_{}\dots ,}$ $(\$이 $긍정적$인 방향을 갖도록 합니다.

이것은 e ${\displaystyle {1\mathrm{}}_{}}$×${\displaystyle }$× × ${\displaystyle {}_n}$ - ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle e_{}}$n { \ $display style$ e$_${ $n$1} \ times \ $cdots$\$times$ e _ { $n$} , ${\displaystyle {e\mathrm{}}_{}}$2 ×${\displaystyle \times }$ × ${\displaystyle e_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {e\mathrm{}}_{}}$1$$, \ $display style$ e$_$ { 2 } \ $times$\ $cdots$ e _ { $n$} = e _ { n } 로 $평가$되는 고유한 다선형 교대 제품입니다$.$

좌표에서 R의ⁿ 교차곱의${\displaystyle }$(${\displaystyle n}$-${\displaystyle 1}$)$${$displaystyle (n-1)}$ -ary 아날로그에$$ 대한 공식을 다음과 같이 나타낼 수 있다.

${\displaystyle \bigwedge _{i=0}^{n-1}\mathbf {v}_{i}=matrix {vmatrix}v_{1}^{1}&\cdots &\vdots &\vdots \\vdots {n-1}^{1-1} & cdots & cdots}$

이 공식은 기초 벡터의 행이 첫 번째 행이 아니라 행렬식의 마지막 행이라는 점을 제외하고 R의³ 정규 교차곱의 행렬식 공식과 구조가 동일하다.그 이유는 순서가 매겨진₁ 벡터(v_n−1, ..., v^n–1
_i=0i, δv₁)가 (e_n, ..., e)에 대해 양의 방향을 갖도록 하기 위해서입니다.n이 홀수일 경우 이 수정은 값을 변경하지 않으므로 이 규칙은 이진 곱의 정규 정의와 일치합니다.단, n이 짝수인 경우에는 구별을 유지해야 합니다.$({\displaystyle n}$ -${\displaystyle 1}$ )$$\ $displaystyle$( n -$1$ ) - ary$$ 형식은 벡터 크로스 곱과 동일한 특성을 많이 가지고 있습니다. 즉, 인수가 번갈아 선형이며, 각 인수에 수직이며, 인수에 의해 둘러싸인 영역의 하이퍼볼륨을 제공합니다.벡터 교차 곱과 마찬가지로, 이것은 좌표 독립적인 방식으로 인수의 쐐기 곱의 호지 쌍으로 정의될 수 있습니다.

역사

1773년, Joseph-Louis Lagrange는 4면체를 ^{[23][note 3]}3차원으로 연구하기 위해 점곱과 교차곱의 성분 형태를 모두 사용했습니다.

1843년, 윌리엄 로완 해밀턴은 4분의 1의 곱과 함께 벡터와 스칼라라는 용어를 도입했다.두 사분위수 [0, u]와 [0, v]가 주어졌을 때, 여기서 u와 v는 R의³ 벡터이며, 이들의 사분위수 곱은 [-u v v, u × v]로 요약할 수 있다.제임스 클럭 맥스웰은 해밀턴의 4분의 1 도구를 그의 유명한 전자기 방정식을 개발하기 위해 사용했고, 이것과 다른 이유들로 인해 한동안 4분의 1은 물리학 교육의 필수적인 부분이었다.

1844년에 헤르만 그라스만은 2차원이나 3차원에 얽매이지 않는 기하학적 대수를 발표했다.Grassmann은 당시 [uv]^[24]로 표현된 교차 제품을 포함하여 여러 제품을 개발합니다.(「외부 대수」도 참조).

1853년, 그라스만의 동시대인인 아우구스틴 루이 코치는 방정식을 푸는 데 사용되었고 ^[25][26]교차곱과 같은 곱셈 특성을 가진 대수 키에 관한 논문을 발표했다.

1878년, 윌리엄 킹든 클리포드는 벡터 곱이라는 용어가 증명된 동적 요소를 출판했다.이 책에서 두 벡터의 곱은 그들이 양변인 평행사변형의 면적과 같은 크기와 그들의 ^[27]평면에 수직인 방향을 갖는 것으로 정의된다.(Clifford 대수 참조).

1881년 강의 노트에서 깁스는 교차곱을 u ×$displaystyle$u\$times$ v$)$로 나타내며 이를 스큐 ^[28][29]곱이라고 부릅니다.1901년 깁의 제자 에드윈 비드웰 윌슨은 이 강의 노트를 편집하고 교과서 벡터 분석으로 확장합니다.Wilson은 스큐 곱이라는 용어를 유지하지만 교차곱과^{[note 4]} 벡터 곱의 대체 항이 더 ^[30]자주 사용되는 것을 관찰합니다.

1908년, Cesare Burali-Forti와 Roberto Marcolongo는 벡터 곱 표기법 u v ^[24]v를 도입했다.기호$$×({$displaystyle\times})$는 곱셈과 데카르트 곱을 나타내는 데 이미 사용되고 있기 때문에 프랑스 등에서는 오늘날까지 사용되고 있습니다.

「 」를 참조해 주세요.

• 데카르트 제품 – 2세트 제품
• 기하학 대수: 회전계
• 다중 크로스 제품 – 3개 이상의 벡터가 포함된 제품
• 벡터의 곱셈
• 4중 제품
• × (기호)

메모들

레퍼런스

참고 문헌

• Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. p. 134. ISBN 978-0-486-67766-8.
• Crowe, Michael J. (1994). A History of Vector Analysis. Dover. ISBN 0-486-67910-1.
• E. A. Milne(1948) 벡터 역학, 2장: 벡터 곱, 페이지 11-31, 런던:메튜엔 출판사
• Wilson, Edwin Bidwell (1901). Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale University Press.
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (in Italian). Bologna: Zanichelli editore.

외부 링크

• "Cross product", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 교차 곱의 기하학적 도출 및 해석
• 시러큐스 대학에서 작성된 인터랙티브 튜토리얼– (java 필요)
• W. Kahan (2007).유클리드 2-공간과 3-공간에서의 교차 산물과 회전.캘리포니아 대학교 버클리(PDF)
• 벡터 제품, Mathcentre(영국), 2009