하이젠베르크 군

수학에서, 베르너 하이젠베르크의 이름을 딴 하이젠베르크 $군{\displaystyle }$H(\$displaystyle$ H$)$는 3×3개의 상위 삼각형 행렬의 군이다.

$(\displaystyle {pmatrix} 1&a&c\0&b\0&1\end {pmatrix})$

행렬 곱셈의 연산 아래.원소 a, b 및 c는 동일성이 있는 임의의 교환환에서 얻을 수 있으며, 종종 실수환('연속 하이젠베르크 군'의 결과) 또는 정수환('이산 하이젠베르크 군'의 결과)으로 간주된다.

연속 하이젠베르크 그룹은 1차원 양자역학계의 기술, 특히 스톤-본 노이만 정리의 맥락에서 발생한다.보다 일반적으로, 사람들은 N차원 시스템, 그리고 가장 일반적으로, 심플렉틱 벡터 공간에 관련된 하이젠베르크 그룹을 고려할 수 있다.

3차원 케이스

3차원의 경우, 2개의 하이젠베르크 행렬의 곱은 다음과 같이 주어진다.

$(\displaystyle {pmatrix} 1&a&c\\end {pmatrix} 1&c'\displaystyle {pmatrix} 1&c'\displaystyle {pmatrix} 1&c'\display {pmatrix} 1&a+a&c'1&c'\display {pmatrix}}$

ab'라는 용어에서 알 수 있듯이, 그 그룹은 비-벨리안이다.

하이젠베르크 그룹의 중성 원소는 항등 행렬이며, 역행렬은 다음과 같이 주어진다.

$({displaystyle {pmatrix} 1&a&c\\0&1&b} {{pmatrix}} = {pmatrix} 1&a&ab-c\0&1-b\0&1\end {pmatrix} ) 。}$

는 2차원 아핀 그룹의 그룹은 하위 그룹 Aff(2):(1c01b001){\displaystyle{\begin{pmatrix}1&, a&, c\\0&, 1&, b\\0&, 0&, 1\\\end{pmatrix}}}()→, 1){\displaystyle({\vec{x}},1)}에서 작용하는 affine 대해 변형(101에 해당합니다. )x →+( b $)({$

이 3차원 사례에는 몇 가지 두드러진 예가 있다.

연속 하이젠베르크 군

a, b, c가 (환 R 내의) 실수라면, 1은₃ 연속적인 하이젠베르크 군 H(R)를 가진다.

차원 3의 전혀 쓸모없는 실제 Lie 그룹입니다.

실제 3×3 행렬로서 표현되는 것 외에, 연속 하이젠베르크 군에는 함수 공간의 관점에서 몇 가지 다른 표현이 있다.스톤-본 노이만 정리에 따르면, 동형사상까지, H의 중심이 주어진 중요하지 않은 특성에 의해 작용하는 독특한 환원 불가능한 단일 표현법이 있다.이 표현에는 몇 가지 중요한 깨달음 또는 모델이 있습니다.슈뢰딩거 모형에서 하이젠베르크 군(Group)은 제곱적분함수의 공간에 작용합니다.세타 표현에서, 그것은 위쪽 반평면의 정형함수 공간에 작용한다; 그것은 세타함수와의 연관성 때문에 이름이 붙여졌다.

이산 하이젠베르크 군

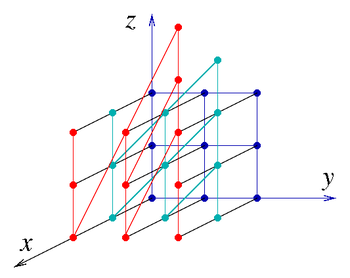
만약 a, b, c가 (고리 Z 내의) 정수라면, 하나는 이산 하이젠베르크 군 H₃(Z)를 가진다.그것은 비벨리안이 아닌 무능력 집단이다.발전기가 두 개 있고

$({displaystyle x=pmatrix}1&0&1&0\\0&1\\end{pmatrix}), \y=pmatrix}1&0&1&0&1\end{pmatrix})$

및 관계

${\displaystyle {}_{}^{}\text{z}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle x}$ y${\displaystyle {}^{}}$ - ${\displaystyle 1^{}{}^{}{}^{}{}^{}}$ -${\displaystyle {}^{}{1}^{}}$ , x ${\displaystyle z}$ ${\displaystyle =}$ ${\displaystyle z}$x , ${\displaystyle \text{y}}$ ${\displaystyle z}$ $=$ ${\displaystyle z}$y { \ $displaystyle z_${ }^{ - $1$} $y^{$ - $1$} , \ $xz$=$zx$, \ $yz$=$zy$} ,

어디에

$({displaystyle z=pmatrix}1&1\\0&1\\end{pmatrix})$

는 H 중심₃ 생성기입니다(x, y 및 z의 역수는 대각선 위의 1을 -1로 대체합니다).

베이스의 정리에 따르면, 그것은 4차 다항식 성장률을 가진다.

모든 요소를 생성할 수 있습니다.

${\displaystyle {pmatrix}1&a&c\0&1&1\end {pmatrix}=y^{b}z^{c}x^{a},}$

하이젠베르크 군 모듈로 홀수 소수 p

홀수 소수 p에 대해 Z/p Z의 a, b, c를 취하면 하이젠베르크 군 모듈로 p를 갖는다.생성기 x, y 및 관계를 갖는 순서³ p의 그룹입니다.

$\displaystyle z_{}^{-1}y^{-1},\x^{p}=y^{p}=z^{p}=1,\xz=zx,\yz=zy.}$

홀수 소수 p의 유한체 위에 있는 하이젠베르크 그룹의 유사체는 특별군, 또는 더 적절하게는 지수 p의 특별군이라고 불린다.보다 일반적으로, 그룹 G의 파생 부분군이 G의 중심 Z에 포함되어 있다면, G/Z × G/Z → Z로부터의 지도는 아벨 군에서 스큐-쌍선형 연산자이다.

단, G/Z가 유한 벡터 공간인 것을 요구하려면 G의 Frattini 부분군을 중심에 포함해야 하며, Z가 Z/p Z 위의 1차원 벡터 공간인 것을 요구하려면 Z가 차수 p를 가져야 하므로 G가 아벨리안이 아니라면 G는 더욱 특별하다.만약 G가 특별히 특수하지만 지수 p를 가지지 않는다면, 심플렉틱 벡터 공간 G/Z에 적용되는 아래의 일반 구조는 G와 군 동형성을 가지지 않는다.

하이젠베르크 군 모듈로 2

하이젠베르크 군 모듈로 2는 8차이고 이면체 군₄ D(사각형의 대칭)와 동형이다.주의해 주십시오.

( 1 1) , ( 1), y = $display style$ x $= display$ { $pmatrix } 1$ &$1$ & 0 \ 0 &$1$ \ \$0$ & $0$& $1$\ \ \ \ 0 & 0 & 1 \ \ \ \ \ 0 & 1 \ \ $y = display$ { $pmatrix }$1 & 0 $pmatrix }$1 & 1 & 1 & 1 & 1$、$ 0 \ 0 \ 0 \ 0 \ 0 \ 0 \ 1 。

그리고나서

$({displaystyle xy=pmatrix}1&1\\0&1\\end{pmatrix})$

그리고.

$({displaystyle yx=pmatrix}1&0&1\end{pmatrix})}$

x와 y 요소는 반사(45° 사이)에 해당하는 반면 xy와 yx는 90° 회전에 해당합니다.다른 반사는 xyx와 yxy이며 180° 회전은 xyxy(=yxyx)입니다.

하이젠베르크 대수

하이젠베르크 $그룹{\displaystyle }$ H$($$실수$$$위에$$ $있는$$)$의 $리$는 $하이젠베르크$ ^[1]대수로 알려져 있다.이것은^[2] 형태의 3×3 행렬의 공간을 사용하여 나타낼 수 있다.

$(\displaystyle {pmatrix} 0&c\0&b\0&0&0\end {pmatrix}}$

a${\displaystyle ,}$ ${\displaystyle b,}$ ${\displaystyle cr\mathbb{}}$R {\$displaystyle$ a,$b, c\in \mathbb {R}$$}$로 지정합니다.

다음 3가지 요소는$$h의 $기본$이 $됩니다$.\style {$mathfrak$ { h$\}$ 。

$({displaystyle X=pmatrix}0&1\0&0&0\\0&0&0\\end{pmatrix};\quad Y=pmatrix}0&0&1\0&0&0&0&1\end{pmatrix};\quad Z=pmatrix0&0&0&0&0&0&0&0})}$

이러한 기본 요소들은 정류 관계를 만족시킵니다.

${\displaystyle [X}$ , ${\displaystyle Y}$] ${\displaystyle =Z}$; [${\displaystyle X}$ ,${\displaystyle Z}$ ] ${\displaystyle =0}$; [${\displaystyle Y}$ , ${\displaystyle Z}$] ${\displaystyle =}$ \ $displaystyle [ X$ , Y ] =$$Z ; \$quad [ X$ , Z ] =$$0 ; \$quad [ Y$ , Z ] $= 0$ $\}$

"하이젠베르크 군"이라는 이름은 양자역학에서의 표준 정류관계와 같은 형태를 가진 앞의 관계에서 유래되었다.

$\displaystyle \left[{\hat {x}}\right]=I\hbar I;\quad \left[{\hat {x}},i\hbar I\right]=0;\quad \left[{\hat {p},i\hbar I\right]=0,$

$여기$서 x$^$ ${\displaystyle {x}}$은 위치$$ 연산자, p$^$ ${\$$displaystyle$ {$p}는$운동량 연산자,$\$ {\displaystyle \$hbar}$는 플랑크의 상수입니다.

하이젠베르크 그룹 H는 지수맵이 일대일이라는 특수성을 가지고 있으며, 리 $대수{\displaystyle \mathfrak{}}$h$(\displaystyle\mathfrak {$h})에서 그룹 ^[3]H로의 지도 위에 있다.

$(\displaystyle\exp {pmatrix}0&c\\end {pmatrix}=pmatrix}1&c+{\frac {ab}{2}}\0&b\0&1\end{pmatrix}).}$

고차원

보다 일반적인 하이젠베르크 $군{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{H2n}}_{}}$ ${\displaystyle {+}_{}}$(\$displaystyle H_{2n+1})$은 유클리드 공간에서의 고차원에 대해, 그리고 보다 일반적으로 심플렉틱 벡터 공간에 대해 정의할 수 있다.가장 단순한 일반적인 케이스는 임의의 $정수{\displaystyle }$ n$1$1(\$displaystyle$ n$\geq$1$)$에 대해 $치수{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{2n}}$ +$$1$(\backslash$$displaystyle 2n + 1$)의 실제 하이젠버그 그룹입니다.행렬의 그룹으로서 ${\displaystyle {\mathrm{H2n}}_{}}$${\displaystyle {+}_{}}$(\$displaystyle H_{2n + 1$${\displaystyle {}_{}}$R)\display H_{2n + ${\displaystyle 1_{}}$(\mathbbbb$)$ver 필드 $($실수의 \$displaystyle \mathbb {R})$은 R$(\$의 엔트리를 가진 그룹$({\displaystyle \mathrm{n}}$ ${\displaystyle +}$2${\displaystyle )}$× (${\displaystyle n}$+$)\times (n+2)$ 행렬로$$ 정의되며 다음 형식을 가집니다.

${\displaystyle {begin{bmatrix}1&\mathbf {a}&\mathbf {0}&\mathbf {0}&\end {bmatrix}}$

어디에

a는 길이 n의 행 벡터입니다.

b는 길이 n의 열 벡터이다.

I는_n 크기 n의 항등 행렬이다.

그룹 구조

이는 곱셈에서 알 수 있듯이 실제로 그룹입니다.

${\displaystyle {bmatrix}1&\mathbf {a}&c\0&I_{n}&\mathbf {b}\0&1\end {bmatrix}\cdot {begin {bmatrix}1&\mathbf {a} '&c'\0&I_{n}&\mathbf {b}'\0&1\end{bmatrix}="{bmatrix}1&\mathbf {a} +\mathbf {a} \cdot \mathbf {b}'\0&"I_{n}&\mathbf {b} +\mathbf {b} '\0&1\end {bmatrix}}$

그리고.

${\displaystyle {bmatrix}1&\mathbf {a}&c\0&I_{n}&\mathbf {b}\0&1\end{bmatrix}\cdot {begin{bmatrix}1&-\mathbf {a}\cdot \mathbf {b} \\0&I_{n}&-\mathbf {b} \\0&1\end {bmatrix} = begin { bmatrix }1&0\0&0&I_{n}&0\\0&1\end {bmatrix}.}$

리 대수

하이젠베르크 그룹은 단순히 연결된 리 군으로, 리 대수는 행렬로 구성되어 있다.

$({displaystyle {bmatrix} 0&\mathbf {a}&c\0&0_{n}&\mathbf {b}\\0&0&end {bmatrix})$

어디에

a는 길이 n의 행 벡터입니다.

b는 길이 n의 열 벡터이다.

0은_n 크기 n의 0 행렬입니다.

e, ..., e를_n R의 표준ⁿ 베이스로 하고₁,

${\displaystyle{\begin{정렬}p_{나는}&, ={\begin{bmatrix}0&,\operatorname{e}_{나는}^{\mathrm{T}}&0\\0&, 0_{n}&, 0\\0&, 0&, 0\end{bmatrix}},\\q_{j}&, ={\begin{bmatrix}0&, 0&, 0\\0&, 0_{n}&,\operatorname{e}_{j}\\0&, 0&, 0\end{bmatrix}},\\z&, ={\begin{bmatrix}0&, 0&, 1\\0&, 0_{n}&, 0\\0&, 0&, 0\end{bmatr.ix}},\end{정렬}}}$

연관된 리 대수는 표준 정류 관계에 의해 특징지어질 수 있다.

${\displaystyle {bmatrix}p_{i},q_{j}\end{bmatrix}=\displaystyle {ij}z,\qquad {bmatrix}p_{i},z\end{bmatrix}=0,\qquad {bmatrix}=0,$

(1)

여기서₁ p, ..., p_n, q₁, ..., q_n, z는 대수 생성기입니다.

특히, z는 하이젠베르크 리 대수의 중심 요소이다.하이젠베르크 그룹의 리 대수는 영가치가 없다는 점에 유의하십시오.

지수 지도

허락하다

${\displaystyle u=syslog{bmatrix}0&\mathbf {a}&c\0&0_{n}&\mathbf {b}\0&0&end{bmatrix}}},$

이는 ${\displaystyle {\mathrm{}}_{}}$ 3 $=$ 0${\displaystyle n_{}}$ + $({$ u$^{3$}=$0_{n+2$를 $충족$합니다.지수 맵은 다음과 같이 평가됩니다.

${\displaystyle \exp(u)=\sum _{k=0}^{\infty}{\frac {1}{k!}}u^{k}=I_{n+2}+u+{\tfrac {1}{2}}u^{2}={bmatrix}1&\mathbf {a}&c+{1 \over2}\mathbf {a} \cdot \mathbf {b} \\0&I_{n}&\mathbf {b} \\0&1\end {bmatrix}.}$

영가수 리 대수의 지수 맵은 리 대수와 연결된, 단순하게 연결된 고유한 리 군 사이의 미분 동형이다.

(치수와 Lie 그룹에 관한 문장에서 제외) 이 설명은 R을 임의의 가환환 A로 치환하는 경우에 더욱 적용됩니다.대응하는 그룹은 H(A)로 표시됩니다_n.

소수점 2가 링 A에서 반전가능하다는 추가 가정 하에 지수맵도 정의된다.이는 유한합으로 감소하여 위의 형태를 가지기 때문이다(예를 들어 A는 홀수 소수점 p 또는 특성 0의 임의의 필드를 갖는 링 Z/p Z일 수 있다).

표현 이론

하이젠베르크 그룹의 유니터리 표현 이론은 상당히 단순하며, 나중에 맥키 이론에 의해 일반화되며, 아래에서 논의된 것처럼 양자 물리학에서 그것이 도입된 동기가 되었다.

0이 아닌 실수$${\(\$display$$style$ \$hbar$에 $대해{\displaystyle }$ ${\displaystyle {\mathrm{H2}}_{}}$${\displaystyle {}^{}}$n +$$(\$displaystyle H_{$$2n+$$1})$의 축소 불가능한 유니터리 표현 $(\$$displaystyle$$\Pi_{\$$hbar})$을 ${\displaystyle {정의}^{}}$할 수 있습니다$.$

$\displaystyle \left[\Pi _{\hbar}{\begin{pmatrix}1&\mathbf {a}&c\0&I_{n}&\mathbf {b}\0&1\end{pmatrix}\psi \right](x)=e^{i\hbar c}e^{ib\cdot x}\psi(x+\hbar a)}$

이 표현은 슈뢰딩거 표현으로 알려져 있다.이 표현의 동기는 양자역학에서 지수화된 위치와 운동량 연산자의 작용이다.$파라미터{\displaystyle }$ a$(\displaystyle$ a$)$는 위치공간의 변환을 나타내고 $파라미터{\displaystyle }$b(\$displaystyle$ b$)$는 운동량공간의 변환을 나타내며 $파라미터{\displaystyle }$c(\$displaystyle$ c$)$는 전체적인 위상계수를 나타냅니다.위상 계수는 위치 공간에서의 변환과 운동량 공간에서의 변환은 이동하지 않기 때문에 연산자 그룹을 얻기 위해 필요합니다.

이는 본부 중대한 체하는 것이 하이젠베르크 그룹의 모든( 강하게 연속) 할 수 있는 일원화된 표현을 일부ℏ{\displaystyle \hbar}.[5]에 또는 ℏ{\displaystyle \Pi_{\hbar}}Π에, 그들 모두가 찾는 것 등가 있다고 주장하는 핵심적인 결과는 Stone–von 노이만 정리,.eW차원 2n의 심플렉틱 공간에서의 eyl 대수(또는 CCR 대수)입니다.

하이젠베르크 그룹은 $n의$1차원 중심 $확장$이므로$,$ 그 환원 불가능한 유니터리 표현은 $n의$ 불가능한 유니터리$투영$ 표현으로 볼 수 있다$.$ 개념적으로는 위의 구성 qua에 $주어진$ 표현이다.ntum 기계적인 부분, $고전{\displaystyle {\mathbb{}}^{}}$ 위상 공간의 변환 대칭 그룹에 대한 부분, ${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\mathrm{2n}}^{}}$ $\$양자 버전이 ${\displaystyle {\mathrm{}}^{}}$ $(\$})의 투영 표현일 뿐이라는 사실은 이미 고전적인 수준에서 제안되고 있다.위상 공간에서의 해밀턴 변환 생성기는 위치 및 운동량 함수입니다.그러나 이러한 함수의 스팬은 포아송 괄호 아래에 Lie 대수를 형성하지 않습니다. ${\displaystyle {}_{}}{\displaystyle }${ ${\displaystyle x_{}}$i , ${\displaystyle {}_{}}$ ${\displaystyle j_{}}$} ${\displaystyle =}$ ${\displaystyle {\delta }_{}}$i , j$$. { $displaystyle$\ {$x$_ {i _ {i } \ displaystyle \ {x _ {$i$} \ sp _ {j} = \ displaystyle _ {i , j$}$ } } } rather$$ _ {i , j} } } rather _ _ _ _ _ _ _ _ _ _ _ _ _ _ 、 { i rather functions _ { i rather _ { i rather _ _ _이 리 대수는 하이젠베르크 ${\displaystyle {}^{}}$의 리 대수와 동형인 교환 리 $대수$ $n의$1차원 중심 $확장$이다$.$

심플렉틱 벡터 공간에서

하이젠베르크 군의 일반적인 추상화는 심플렉틱 벡터 ^[6]공간에서 만들어진다.예를 들어, (V, θ)를 유한 차원 실심플렉틱 벡터 공간이라고 하자(따라서 θ는 V 위의 비변형 스큐 대칭 쌍선형 형태).하이젠베르크 군 H(V) on (V, )) (또는 간단히는 V)는 군법칙이 부여된 집합 V×R이다.

${\displaystyle (v,t)\cdot \left (v',t'\right)=\left (v+v',t+t'+{\frac {1}{2}}\obe \left (v,v'\right)\right.}$

하이젠베르크 그룹은 가법군 V의 중심 확장체이다.따라서 정확한 순서가 있다.

${\displaystyle 0\to\mathbf {R}\to H(V)\to V\to 0.}$

모든 심플렉틱 벡터 공간은 θ(e_jj, f^kk)_{1 ≤ j,k ≤ n} = θ를_j^k 만족하고 여기서 2n은 V의 차원이다(V의 차원은 필연적으로 짝수이다).이 기준에서, 모든 벡터는 다음과 같이 분해된다.

${\displaystyle v=q^{a}\mathbf {e}_{a}+p_{a}\mathbf {f}^{a}.}$

q와_a p는^a 규범적으로 공역 좌표이다.

{e_j, f^k}_{1 ≤ j,k ≤ n}이(가) V의 Darboux 기준이면 {E}이(가) R의 기준이고 {e_j, f^k, E}_{1 ≤ j,k ≤ n}이(가) V×R의 해당 기준입니다.다음으로 H(V)의 벡터는 다음과 같이 주어진다.

${\displaystyle v=q^{a}\mathbf {e}_{a}+p_{a}\mathbf {f}^{a}+tE}$

그리고 단체법은

$\displaystyle (p,q,t)\cdot \left(p',q',t'\right)=\left(p+p',q+q',t+t'+{\frac {1}{2}}(pq'-p'q)\right.}$

하이젠베르크 그룹의 기초 다양체는 선형 공간이기 때문에, 리 대수의 벡터는 군 내의 벡터와 규범적으로 동일시 될 수 있다.하이젠베르크 군의 리 대수는 정류 관계에 의해 주어진다.

$({displaystyle {bmatrix}(v_{1}, t_{1}), (v_{2})\end{bmatrix}}=\obega(v_{1}, v_{2})$

다르부어 베이스로 쓰여져 있다.

${\displaystyle \left[\mathbf {e} _{a},\mathbf {f}^{b}\right]=\displaystyle _{a}^{b}}$

다른 모든 정류자는 사라집니다.

또한 그룹 법칙을 다른 방식으로 정의할 수도 있지만, 이는 방금 정의한 그룹과 동일한 그룹을 생성합니다.혼란을 피하기 위해, 우리는 t 대신에 u를 사용할 것이다. 그래서 벡터는 다음과 같이 주어진다.

${\displaystyle v=q^{a}\mathbf {e}_{a}+p_{a}\mathbf {f}^{a}+uE}$

그리고 단체법은

$\displaystyle (p,q,u)\cdot \left(p',q',u'\right)=\left(p+p',q+q',u+u'+pq'\right.}$

그룹의 요소

${\displaystyle v=q^{a}\mathbf {e}_{a}+p_{a}\mathbf {f}^{a}+uE}$

그러면 행렬로 표현될 수 있다.

$]{$$I_{n}&q\0&1\end{bmatrix}},$

이것은 H(V)의 충실한 행렬 표현을 제공한다.이 식에서 u는 ${\displaystyle u=}$ ${\displaystyle t}$ + ${\displaystyle 1}$ 2 p$$q {\$displaystyle u=t+{\tfrac {1}{2$}}pq$\}$로 이전 식에서 t와 관련이 있으므로 제품의 t 값은 다음과 같습니다.

$display$$\={}&t+{\frac {1}{2}}pq+t'+{\frac {1}p'q'+pq'-{\frac {1}{2}\left(p+p'\right)\left(q+q'\오른쪽)$$\\={}&t+t'+{\frac {1}{2}}\left(pq'-p'q\right)\end{aligned}},$

종전과 같이

상부 삼각 행렬을 사용하는 그룹에 대한 동형성은 V u U u U *의 선택에 해당하는 Darboux 기법으로의 V 분해에 의존한다.새로운 군법칙은 더 높은 곳에 주어진 군과 동형성을 가지지만, 이 법칙을 가진 군을 때때로 편광 하이젠베르크 군이라고 부르기도 한다(라그랑주 부분공간의 선택은 편광이다.

어떤 리 대수에도, 독특하고 단순하게 연결된 리 군 G가 있습니다.G와 같은 Lie 대수를 갖는 다른 모든 연결 Lie 그룹은 G/N 형태이며, 여기서 N은 G의 중심 이산 군이다.이 경우 H(V)의 중심은 R이고 유일한 이산 부분군은 Z와 동형입니다.따라서 H(V)/Z는 이 Lie 대수를 공유하는 또 다른 Lie 군이다.이 Lie 그룹에 대해 주목할 점은 그것이 충실한 유한 차원 표현을 허용하지 않는다는 것이다; 그것은 어떤 행렬 군과도 동일하지 않다.그러나 이것은 잘 알려진 무한 차원 단일 표현 패밀리를 가지고 있다.

와일 대수와의 연관성

하이젠베르크 그룹의 라이 $대수{\displaystyle {\mathfrak{}}_{}}$ $(\$은 (1) 행렬의 라이 대수로서 설명되었다.Poincaré-Birkhoff-Witt 정리는 보편 $포락대수{\displaystyle }$U$({\mathfrak$${$$h}}_$${n$$\})$를 결정하는 데 적용된다. 다른 특성들 중에서, 보편 포락대수는 n$(\displaystyle {h}}$_n})이 주입하는$$ $연관{\displaystyle {\mathfrak{}}_{}}$ 대수이다.

따라서 푸앵카레-비르호프-윗 정리에 의해, 이것은 단수물질에 의해 생성되는 자유 벡터 공간이다.

${{displaystyle z^{j}p_{1}^{k_{2}^{k_{n}^{k_{n}}q_{1}^{\ell_{2}^{{2}}\cdots q_{n}^{n}^{\ell_{n}~},{1}^{\cdotsq_{n}$

여기서 지수는 모두 음이 아닙니다.

따라서 U${\displaystyle (h_{}}$n$$) {$displaystyle$ U$({\mathfrak {h}}_{n})}$는 실수 다항식으로 구성됩니다.

${\displaystyle \sum _{j,{\vec {k}},{jvec {k}},{vec {k}},{z^{j}p_{1}{k_{2}}\cdots_{n}{k},{k}{n}},{k}{{q}}},{\vecdots_1},{n}},{n}},{n}}},{n},{n}},{cdots}}},{cdots},{cdvec},{$

치환 관계와 함께

${\displaystyle p_{k}p_{\ell}p_{k}=q_{\ell}q_{k},\display p_{k}q_{\ell}q_{\ell}-q_{\ell}p_{k}=displaystyle _ {\ell}p}z,$

$대수{\displaystyle }$ U${\displaystyle (}$ ${\displaystyle h_{}}$n$$) {$style$ U$({\mathfrak {h}}_{n})}}$는 다항식 계수를 갖는 δⁿ 위의 미분 연산자의 대수와 밀접하게 관련되어 있다. 왜냐하면 그러한 연산자는 형태에서 고유한 표현을 가지고 있기 때문이다.

${\displaystyle P=\sum _{\vec {k}},{\vec {k},{\vec {k}},\vec _{x_{1},\vec _ {k_1},\cdots _ {k_{2}},{cdots \{x_{n}_{k}},{x}},{k},{n}},{\vec {\vec {\},{\vec},{\vec},{\vec},{\vec},{cdots},{$

이 대수는 바일 대수라고 불린다.Weyl 대수_n W는 U${\displaystyle }$( ${\displaystyle {}_{}{n}_{}}$) { $displaystyle$ U ( { \ $mathfrak { h$}}$_$ {$n$} )$$}의 몫이라는 추상적인 넌센스로부터 이어집니다.다만, 이것 또한 위의 표현에서 직접 볼 수 있습니다; 매핑에 의해.

${{displaystyle z^{j}p_{1}^{k_{2}^{k_{n}^{k_{n}}q_{1}^{\ell_{2}^{{2}\cdots q_{n}^{{n}^{\ell_{n},\mapsto\{x}^{{1}}{{{n}}}}}}}{{\cdotsq_{{\cdots}}}}}}{k_n}}}}}{{{{k_{k_{{{{{$

적용들

와일의 양자역학 파라미터화

헤르만 바일을 하이젠베르크 그룹의 명확한 실현으로 이끈 응용은 슈뢰딩거 그림과 하이젠베르크 그림이 왜 물리적으로 동등한지에 대한 질문이었다.추상적으로, 그 이유는 스톤-본 노이만 정리이다: 중심 리 대수 요소 z의 주어진 작용에 대한 독특한 유니터리 표현이 있다. 단일한 등가까지: 대수에서 중요하지 않은 요소들은 모두 통상적인 위치와 운동량 연산자와 동등하다.

따라서 슈뢰딩거 그림과 하이젠베르크 그림은 동등합니다.이러한 그림은 본질적으로 독특한 표현을 실현하기 위한 다른 방법일 뿐입니다.

세타 표현

데이비드 멈포드는 아벨 변종을 정의하는 방정식의 이론에서 이산 하이젠베르크 군을 위해 동일한 고유성 결과를 사용했습니다.이것은 야코비 타원함수에 사용된 접근방식의 큰 일반화이며, 이는 8차 모듈로 2 하이젠베르크 군의 경우이다.가장 간단한 경우는 Heisenberg 그룹의 Theta 표현으로, 이산적인 경우는 Theta 함수를 제공한다.

푸리에 분석

하이젠베르크 그룹은 푸리에 분석에서도 발생하며, 여기서 스톤-본 노이만 정리의 공식에 사용된다.이 경우, 하이젠베르크 그룹은 정사각형 적분 가능 함수의 공간에 작용한다고 이해할 수 있습니다. 그 결과는 바이엘 표현이라고도 불리는 하이젠베르크 군의 표현입니다.

서브리만 다양체로서

실수의 3차원 하이젠베르크 군₃ H(R)도 매끄러운 다양체, 구체적으로는 서브리만 ^[7]다양체의 단순한 예로 이해할 수 있다.R의³ 점 p=(x,y,z)가 주어졌을 때, 이 지점에서 미분 1-폼 δ를 다음과 같이 정의한다.

$\displaystyle \Theta _{p}=dz-{\frac {1}{2}}\left(xdy-ydx\오른쪽).}$

이 단일 형태는 R의³ 코탄젠트 다발에 속합니다.즉,

$\displaystyle \Theta _{p:T_{p}\mathbf {R}^{3}\to \mathbf {R} }$

는 접선 번들의 맵입니다.허락하다

$\displaystyle H_{p}=\left\{v\in T_{p}\mathbf {R}^{3}\mid \Theta _{p}(v)=0\right\}.}$

H는 접선다발³ TR의 부분군임을 알 수 있다.H상의 혜성은 x 및 y방향으로 벡터에 의해 스판되는 2차원 공간에 벡터를 투영함으로써 주어진다.즉, 벡터 $v{\displaystyle }$ $=$ ($$, ${\displaystyle {v\mathrm{}}_{}}$2, ${\displaystyle {}_{}{3\mathrm{}}_{}}$) {$displaystyle$ v=($v_{1}, v_{2$}, $v_{3}})$ $및$ w $=$ ( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}}$w 3)$${$displaystyle$ w=($w_{1$},$w_{$2},$w_{3$}})가$$ TR에³ 지정되면 내부 제품은 다음과 같습니다.

$\displaystyle v,w\rangle = v_{1}w_{1}+v_{2}w_{2}w_{2}.}$

결과 구조는 H를 하이젠베르크 그룹의 다양체로 변화시킨다.다지관의 직교 정규 프레임은 Lie 벡터 필드에 의해 제공됩니다.

${\displaystyle {begin {aligned} X&=beginfrac {\frac x}-{\frac {1}{\frac z},\Y&=beginfrac {1}{\frac {\frac z},\frac {\frac {1}{\frac {\frac z},\frac {\frac z},$

이 값은 [X, Y] = Z 및 [X, Z] = [Y, Z] = 0. Lie 벡터장이므로, 이들은 군 작용에 대한 좌-중립적 기초를 형성한다.다지관의 측지선은 나선형으로 2차원으로 원 아래로 돌출되어 있습니다.즉, 만약

$\displaystyle \display(t)=(x(t),y(t),z(t))}$

는 측지선 ${\displaystyle \mathrm{곡선}}$입니다${\displaystyle .}$곡선 $c{\displaystyle }$ (${\displaystyle }$t ) ${\displaystyle =}$ (${\displaystyle x}$ (${\displaystyle t}$) ,${\displaystyle y}$ ($){$ $display$ c ( t ) = ($x$ ($t$ ) $, y$ ( t ) } } 。는$$ 원의 원호입니다.

${\displaystyle z(t)=black {1}{2}}\int _{c}xdy-ydx}$

적분이 2차원 평면으로 한정되어 있습니다.즉, 곡선의 높이는 원호에 의해 기울어진 원의 면적과 비례하며, 그 다음에 스토크스의 정리가 뒤따른다.

국소 콤팩트 아벨군의 하이젠베르크 군

보다 일반적으로 국소적으로 콤팩트한 아벨 군 K의 하이젠베르크 군을 정의할 수 있으며, Haar ^[8]측도를 갖추고 있다.이러한 그룹에는 K의 모든 $연속{\displaystyle }$U($)$ {\$displaystyle$U(1)$값$ 문자로$$ 구성된 Pontrjagin $듀얼{\displaystyle \stackrel{}{}}$ K$^$ ${\displaystyle {K}}$이$($가) 있으며, 콤팩트 오픈 토폴로지를 가진 경우 로컬 콤팩트 아벨 그룹이기도 합니다.국소 콤팩트 아벨 군 K와 관련된 하이젠베르크 군(Heisenberg group)은 K로부터의 변환과 K$^$의 원소에 의한 곱셈에 의해 ${\displaystyle {생성}^{}}$된 L${\displaystyle {}^{}}$2 $(\displaystyle$ L$^{2}(K)$의 단일군(\$displaystyle$ L^{$K$$\})$의 부분군이다.

보다 자세한 것은, 힐베르트 ${\displaystyle {공간\mathrm{}}^{}}$ L2$K)({displaystyle L^{2}($K)})는$$ K상의 제곱 적분 가능 복소수 $함수{\displaystyle }$ f${style$ f$}$로 구성되어 있다.K의 변환은 K를$)$의 연산자로서의 단일 표현(\$displaystyle$ L$^{2}(K$

${\displaystyle(T_{x}f)(y)=f(x+y)}$

x${\displaystyle ,}$ ${\displaystyle y}$ ${\displaystyle †}$(\$style$ x$,y\in$ K$)$의 $경우{\displaystyle }$.문자별 곱셈도 마찬가지입니다.

$\displaystyle (M_{\chi }f)(y)=\chi(y)f(y)}$

${\displaystyle \chi \stackrel{}{}}$K$^$ { $display style$ \ chi $in \ hat$ { K$\}$ 。이러한 연산자는 통근하지 않고, 대신 만족합니다.

$\displaystyle \left(T_{x}M_{x}T_{x}M_{\chi}^{-1}f\right)(y)=오버라인(\chi(x)}f(y)}}$

고정 단위 계수 복소수에 의한 곱셈.

따라서 K와 관련된 Heisenberg $그룹{\displaystyle }$ H$(K)$ {$displaystyle$ $H($K)}는 ${\displaystyle K\stackrel{}{}}$× K$^(\style$ K\$times {K$의 $중앙{\displaystyle }$ 확장의 일종으로 다음과 같은 그룹의 순서를 따릅니다.

$(\displaystyle 1 to U(1) to H(K) \times \hat {K} \ to 0 . )$

보다 일반적인 하이젠베르크 그룹은 코호몰로지 $그룹{\displaystyle {}^{}}$ ${\displaystyle {H2\mathrm{}}^{}}$( ${\displaystyle K}$,${\displaystyle U}$ (${\displaystyle 1}$ $)\style$ H$^{2}$ ($K , U$ (1$)$)의 2-코실레로 기술됩니다$.$$K$와 $^$ ^ （ $displaystyle K$）의 이중성이 존재하기 때문에 표준적인 코사이클이 발생하지만, 일반적으로는 다른 것도 있습니다.

하이젠베르크 그룹은 ${\displaystyle {L2\mathrm{}}^{}}($$K)$에 $대해{\displaystyle {}^{}}$ 축소할 수 없는 작용을 합니다. 실제로 연속되는 문자는 점을 구분하기^[9] 때문에$K)$의 $단위{\displaystyle {}^{}}$ 연산자 중 L2(K$)$와 일치하는 것은 모두 L2(K$$)\$displaystyle$ L$^{$$2$$}($K)\fty$}$의 승수입니다$.$하지만 번역을 통해 출퇴근하는 것은 승수가 ^[10]일정하다는 것을 의미합니다.

George Mackey에 의해 증명된 스톤-본 노이만 ${\displaystyle \mathrm{정리}}$의 버전은 하이젠베르크 $그룹{\displaystyle }$H (${\displaystyle }$K ) \ $displaystyle$H ( $K$)$$^[11][12]。푸리에 변환은 L ${\displaystyle {2\mathrm{}}^{}}$($K$) \ ${\displaystyle displaystyle\stackrel{}{}}$ $L^{2}$ ( $K$) ) ${\displaystyle {L\mathrm{}}^{}}$2 ( K${\displaystyle \stackrel{}{}^}$) \ $displaystyle$ L$^{2}$ \$left$ ( { \$hat$ { $K}$ \ $right$) $\}$ the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the the

「 」를 참조해 주세요.

• 표준 정류 관계
• 위그너-와일 변환
• 스톤-본 노이만 정리
• 투영 표현

메모들

레퍼런스

• Binz, Ernst; Pods, Sonja (2008). Geometry of Heisenberg Groups. American Mathematical Society. ISBN 978-0-8218-4495-3.
• Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, ISBN 978-1461471158
• Hall, Brian C. (2015). Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. Graduate Texts in Mathematics. Vol. 222 (second ed.). Springer. ISBN 978-3319134666.
• Howe, Roger (1980). "On the role of the Heisenberg group in harmonic analysis". Bulletin of the American Mathematical Society. 3 (2): 821–843. doi:10.1090/s0273-0979-1980-14825-9. MR 0578375.
• Kirillov, Alexandre A. (2004). "Ch. 2: "Representations and Orbits of the Heisenberg Group". Lectures on the Orbit Method. American Mathematical Society. ISBN 0-8218-3530-0.
• Mackey, George (1976). The theory of Unitary Group Representations. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 978-0226500522.

외부 링크

• Groupprops, 그룹 속성 Wiki 유니트라이언귤러 매트릭스 그룹 UT(3,p)