열역학계

열역학 시스템은 벽에 의해 공간에 갇힌 물질 및/또는 방사선의 몸체로, 주변으로부터 분리되는 정의된 투과성을 가지고 있습니다.주변에는 다른 열역학 시스템 또는 열역학 시스템이 아닌 물리적 시스템이 포함될 수 있습니다.열역학 시스템의 벽은 모든 물질, 모든 방사선 및 모든 힘에 대해 '투과성'으로 묘사될 때 순전히 개념적일 수 있습니다.열역학 시스템의 상태는 여러 가지 다른 방법으로, 여러 가지 다른 열역학 상태 변수 세트에 의해 완전히 설명될 수 있습니다.

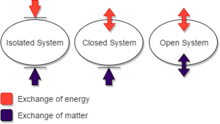
널리 사용되는 구분은 고립, 폐쇄 및 개방 열역학 시스템입니다.

고립된 열역학 시스템은 열을 전도하지 않고 모든 방사선을 완벽하게 반사하는 벽이 있으며, 단단하고 움직이지 않으며, 모든 형태의 물질과 모든 힘에 대해 투과되지 않습니다.(여기서 '고립'이라는 단어를 사용할 때 '닫힘'이라는 단어를 사용하는 작가도 있습니다.)

닫힌 열역학 시스템은 물질에 대해 투과되지 않는 벽에 의해 제한되지만, 열역학 작동에 의해 열에 대해 투과('열열적'이라고 함) 또는 투과되지 않는('단열적'이라고 함) 교대로 만들 수 있으며, 열역학 프로세스(열역학 작동에 의해 시작 및 종료됨)에 대해 교대로 허용되거나 허용하지 않을 수 있습니다.시스템의 체적 변화 또는 교반과 함께 시스템의 내용물에 내부 마찰이 있는 상태에서 움직여야 하며, 열의 기계적 등가물에 대한 Joule의 원래 시연에서와 같이 거칠거나 매끄럽게 하여 표면의 마찰에 의한 시스템 가열이 허용되거나 허용되지 않도록 할 수 있습니다.

개방된 열역학 시스템은 다른 열역학 시스템과 분리되는 적어도 하나의 벽을 가지고 있으며, 이 목적을 위해 개방된 시스템의 주변 환경의 일부로 간주되며, 벽은 적어도 하나의 화학 물질 및 방사선에 투과된다. 개방된 시스템이 열역학 평형 상태에 있을 때, 그러한 벽은 만족하지 않는다.온도차를 스스로 얼룩지게 하다

열역학 시스템은 열역학 작동이라고 불리는 외부 개입의 영향을 받습니다. 이러한 개입은 시스템의 벽이나 주변을 변화시킵니다. 그 결과, 시스템은 열역학 원리에 따라 일시적인 열역학 과정을 거칩니다.이러한 조작과 프로세스는 시스템의 열역학 상태의 변화에 영향을 미칩니다.

그 내용물의 강도 높은 상태 변수가 공간 내에서 변화할 때, 열역학 시스템은 서로 인접한 시스템의 수만큼 고려될 수 있으며, 각각은 다른 열역학 시스템이다.

열역학 시스템은 어떤 벽으로도 서로 분리되지 않은 상호 열역학 평형 상태에서 얼음, 액체 물 및 수증기와 같은 여러 상으로 구성될 수 있으며, 균질할 수도 있다.이러한 시스템은 '단순한' 것으로 간주될 수 있다.

'복합' 열역학 시스템은 각각 확실한 투과성의 하나 또는 여러 벽에 의해 상호 분리된 여러 개의 단순한 열역학 하위 시스템으로 구성될 수 있다.열역학적 평형 상태에서 초기에 격리된 복합 시스템을 고려한 후, 일부 하위 시스템 간 벽 투과성 증가의 열역학적 연산의 영향을 받아 일시적인 열역학적 프로세스를 시작하여 최종적인 새로운 열역학적 평형 상태를 생성하는 것이 종종 편리하다.이 아이디어는 카라테오도리에 의해 사용되었고 아마도 도입되었을 것이다.열역학적 평형 상태에서 초기에 격리된 복합 시스템에서 벽 투과성의 감소는 열역학적 과정이나 열역학적 상태의 변화에 영향을 미치지 않는다.이 차이는 열역학 제2법칙을 나타냅니다.이는 엔트로피 측정의 증가가 미시적 상태의 ^[1]접근성 증가로 에너지 분산의 증가를 나타낸다.

평형 열역학에서, 열역학계의 상태는 비균형 상태와 대조적으로 열역학적 평형 상태를 말한다.

시스템 벽의 투과성에 따라 열역학적 평형 상태에 도달할 때까지 시간과 함께 변하지 않는 것으로 간주되는 에너지와 물질의 이동이 시스템과 주변 사이에서 발생합니다.평형 열역학에서 고려되는 유일한 상태는 평형상태이다.고전 열역학에는 (a) 평형 열역학, (b) 시스템 상태가 아닌 프로세스의 주기적 시퀀스로 고려된 시스템이 포함된다. 이러한 시스템은 주체의 개념적 개발에 역사적으로 중요했다.안정된 흐름에 의해 기술된 프로세스를 지속적으로 유지하는 관점에서 고려되는 시스템은 엔지니어링에서 중요합니다.

열역학 시스템의 상태를 정의하는 열역학 평형의 존재 자체가 열역학의 필수적이고, 특징적이며, 가장 기본적인 가정입니다. 비록 그것이 숫자 ^[2][3][4]법칙으로 거의 인용되지 않습니다.베일린에 따르면, 열역학 제0법칙에 대해 일반적으로 리허설된 진술은 이 기본적인 ^[5]가설의 결과이다.사실, 자연에서 사실상 어떤 것도 엄격한 열역학 평형에 있지 않지만, 열역학 평형의 가정은 종종 이론적으로나 실험적으로 매우 유용한 이상화 또는 근사치를 제공합니다; 실험은 실제 열역학 평형의 시나리오를 제공할 수 있습니다.

평형 열역학에서 상태 변수는 플럭스를 포함하지 않는다. 왜냐하면 열역학적 평형 상태에서는 모든 플럭스가 정의상 0 값을 가지기 때문이다.평형 열역학 과정은 플럭스를 포함할 수 있지만, 열역학 과정 또는 작업이 완료될 때쯤 시스템이 최종 열역학 상태로 전환될 때까지 이러한 과정은 중단되어야 합니다.비균형 열역학에서는 상태 변수가 0이 아닌 플럭스를 포함할 수 있습니다. 즉, 시스템과 ^[6]그 주변 환경 사이의 질량이나 에너지 또는 엔트로피의 전달을 기술합니다.

1824년 Sadi Carnot은 열역학 시스템을 연구 중인 모든 열 엔진의 작동 물질(증기 부피 등)로 설명했습니다.

개요

열역학
고전적인 카르노 히트 엔진
나뭇가지 고전적인 통계 화학의 양자 열역학 평형/비평형
법률 제로스 첫번째 둘째 셋째
시스템들 폐쇄형 시스템 오픈 시스템 격리 시스템 주 상태 방정식 이상 기체 실가스 상황 위상(매터) 평형 볼륨 제어 인스트루먼트 과정 이소바릭 아이소코리 등온 단열성 등엔트로픽 이센탈픽 준정전성 폴리트로픽 자유 확장 가역성 불가역성 내복원성 사이클 히트 엔진 히트 펌프 열효율
시스템 속성 주의: 이탤릭체로 표시된 켤레 변수 속성도 집약적이고 광범위한 속성 프로세스 기능 일하다. 열 국가 기능 온도/엔트로피(개요) 압력/볼륨 화학 퍼텐셜/입자수 증기 품질 속성 감소
재료 특성 속성 데이터베이스 비열 용량 ${\displaystyle c=}$ ${\displaystyle T}$ $\displaystyle \partial S\$ ${\displaystyle N}$ ${\displaystyle\partial T}$ 압축성 $\displaystyle \displays =-}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ $(\displaystyle\displayp)$ 열팽창 $\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ ${\displaystyle\partial T}$
방정식 카르노의 정리 클라우시우스 정리 기본 관계 이상기체의 법칙 맥스웰 관계 온사저 호혜 관계 브리지만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 ${\displaystyle A(T,V)=U-TS}$ 깁스 자유 에너지 ${\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스 법칙 "영구 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너제틱스 이론들 열량론 Vis viva ('생체력') 열의 기계적 등가 동력 주요 출판물 실험적인 질문 ~에 대해서열 균형에 대하여 이종 물질 의 리플렉션 불의 원동력 타임라인 열역학 히트 엔진 예체능 교육 맥스웰의 열역학 표면 에너지 분산으로서의 엔트로피
과학자 베르누이 볼츠만 브리지만 카라테오도리 카르노 클라피론 클라우시우스 돈더 듀헴 깁스 폰 헬름홀츠 줄 루이스 마시외 맥스웰 폰 메이어 네른스트 온사게 플랑크 랭킨 스미톤 스틸 태트 톰슨 톰슨 판 데르 발스 워터스톤
다른. 핵생성 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

열역학적 균형은 질량이나 에너지의 흐름이 없는 것이 특징이다.평형 열역학은 물리학의 과목으로서 내부 열역학적 평형 상태에 있는 물질과 에너지의 거시적 물체를 고려한다.그것은 열역학적 과정의 개념을 사용하는데, 그 과정에서 물체는 물질과 에너지의 전달에 의해 하나의 평형 상태에서 다른 평형 상태로 넘어간다.'열역학계'라는 용어는 열역학의 특수한 맥락에서 물질과 에너지의 물체를 지칭하는 데 사용된다.물체 사이의 가능한 균형은 몸을 분리하는 벽의 물리적 특성에 의해 결정된다.평형 열역학에서는 일반적으로 시간을 측정하지 않습니다.평형 열역학은 비교적 간단하고 잘 정착된 과목이다.이것의 한 가지 이유는 '물체의 엔트로피'라고 불리는 잘 정의된 물리량의 존재이다.

비균형 열역학은 물리학의 과목으로서 내부 열역학적 평형 상태에 있지 않은 물질과 에너지의 물체를 고려하지만, 일반적으로 열역학 상태 변수와 밀접하게 관련된 양으로 기술할 수 있을 만큼 충분히 느린 전달 과정에 참여한다.그것은 물질과 에너지의 흐름으로 특징지어진다.이 주제에서 고려된 신체는 부드러운 공간 불균형을 가지므로, 예를 들어 온도 구배와 같은 공간 구배가 충분히 정의된다.따라서 비균형 열역학 시스템의 설명은 필드 이론이며, 평형 열역학 이론보다 더 복잡하다.비균형 열역학은 확립된 구조가 아니라 성장하는 주제이다.일반적으로 불균형 문제에 대해서는 정확하게 정의된 엔트로피를 찾을 수 없습니다.많은 비균형 열역학적 문제에서, '엔트로피 생산 시간 속도'라고 불리는 대략적으로 정의된 양은 매우 유용하다.비균형 열역학은 이 기사의 범위를 대부분 벗어난다.

공학에서는 또 다른 종류의 열역학 시스템이 고려된다.흐름 프로세스에 관여합니다.그 설명은 많은 경우에 있어서 평형 열역학적 개념에 근접한 것이다.이는 본 문서의 대부분 범위를 벗어나 있으며, 다른 문서(예: 흐름 프로세스)에 설명되어 있습니다.

역사

열역학 시스템의 개념을 최초로 만든 사람은 프랑스의 물리학자 사디 카르노로, 1824년 불의 동력에 대한 성찰은 그가 말하는 작동 물질, 예를 들어 증기 엔진에서 수증기의 몸체라고 불리는 작동 물질에 대해 연구했습니다.작동 물질은 열 저장 장치(보일러), 냉 저장 장치(냉수 흐름) 또는 피스톤(작업 주체가 눌러 작업을 수행할 수 있는)과 접촉할 수 있습니다.1850년 독일의 물리학자 루돌프 클라우시우스는 이 그림을 주변 환경의 개념을 포함시키기 위해 일반화했고, 이 시스템을 "작업하는 기관"이라고 부르기 시작했다.Clausius는 1850년에 쓴 '불의 원동력에 대하여'에서 다음과 같이 썼다.

그는 "(작업 주체에) 부피가 바뀔 때마다 일정량의 작업이 가스나 기체에 의해 이뤄져야 한다.그것은 팽창에 의해 외압을 극복하고, 압축은 외압의 작용에 의해서만 이루어질 수 있기 때문이다.가스 또는 가스 또는 가스 관련 작업 초과는 원칙적으로 소비 또는 생산되는 열의 비례 초과와 일치해야 하며, 가스는 받는 열과 동일한 양의 열을 "주변 매체"에 제공할 수 없습니다.

Carnot 열 엔진 기사는 Carnot이 이상적인 엔진에 대해 설명할 때 사용한 원래의 피스톤-실린더 다이어그램을 보여줍니다. 아래에서는 Carnot 엔진이 현재 사용되는 일반적인 모델임을 보여 줍니다.

그림에서 "작업체"(시스템)는 1850년에 Clausius에 의해 도입된 용어로, 열 Q가 유입되거나 전달되어 작업을 생성할 수 있는 유체 또는 증기체일 수 있습니다.1824년, Sadi Carnot은 그의 유명한 논문인 "불의 동력에 대한 성찰"에서 유체 물체는 물의 증기, 알코올의 증기, 수은의 증기, 영구 기체, 또는 공기 등과 같이 팽창할 수 있는 물질일 수 있다고 가정했다.초기 몇 년 동안 엔진은 여러 가지 구성으로 제공되었으며, 일반적으로_H 보일러에 의해 물이 끓어 올랐습니다_C. Q는 일반적으로 엔진의 별도 부분에 위치한 응축기 형태의 차가운 흐름의 물줄기였습니다.출력 작업 W는 피스톤이 크랭크 암을 돌렸을 때 움직이는 것으로, 일반적으로 도르래를 돌려 침수된 염광에서 물을 끌어올리는 역할을 했습니다.Carnot은 작업을 "높이를 통해 들어올려진 무게"로 정의합니다.

균형 잡힌 시스템

열역학적 평형에서 시스템의 특성은 정의상 시간에 따라 변하지 않는다.평형 상태에 있는 시스템은 평형 상태에 있지 않은 시스템보다 훨씬 간단하고 이해하기 쉽습니다.어떤 경우에, 열역학 과정을 분석할 때, 그 과정의 각 중간 상태가 평형 상태에 있다고 가정할 수 있다.이렇게 하면 분석이 상당히 간단해집니다.

격리된 시스템에서는 내부 재배치가 시간이 경과함에 따라 감소하여 안정적인 상태에 도달하는 것이 지속적으로 관찰됩니다.압력과 온도는 균등해지는 경향이 있으며 물질은 비교적 균일한 하나 또는 몇 개의 상으로 나뉩니다.모든 변화의 과정이 실질적으로 완료된 시스템은 열역학적 평형 상태로 간주됩니다.평형 상태에 있는 시스템의 열역학적 특성은 시간에 따라 변하지 않는다.평형 시스템 상태는 비평형 상태보다 결정론적 방식으로 설명하기가 훨씬 쉽다.

공정이 가역적이 되려면 공정의 각 단계가 가역적이어야 합니다.프로세스의 한 단계를 되돌릴 수 있으려면 시스템이 전체 단계에서 평형 상태에 있어야 합니다.그 이상은 실제로 달성될 수 없다. 왜냐하면 어떤 조치도 시스템을 균형으로부터 교란시키지 않고는 취해질 수 없기 때문이다. 그러나 이상적인 것은 천천히 변화함으로써 도달할 수 있다.

벽들

허용된 전송 유형

벽의 종류별로

벽형	전송 유형
	문제	일하다.	열
물질에 투과할 수 있는.	Y	N	N
에너지 투과성이지만 물질이 침투하지 않는.	N	Y	Y
단열성	N	Y	N
단음성과 물질이 침투하지 않는.	N	N	Y
격리	N	N	N

시스템은 그것을 묶고 그것을 ^{[7][8][9][10][11][12]}주변과 연결하는 벽으로 둘러싸여 있다.종종 벽은 물질이나 에너지의 어떤 형태로든 벽을 통과하는 것을 제한하여 간접적인 연결을 만든다.때때로 벽은 주변과 직접 연결되는 상상의 2차원 닫힌 표면에 지나지 않습니다.

벽은 고정(예: 정용량 원자로) 또는 이동(예: 피스톤)할 수 있다.예를 들어 왕복 엔진에서 고정 벽은 피스톤이 제자리에 잠긴 것을 의미하며, 그러면 일정한 체적 프로세스가 발생할 수 있습니다.동일한 엔진에서는 피스톤이 잠금 해제되어 안팎으로 이동할 수 있습니다.벽은 단열, 발열, 투과성, 투과성 또는 반투과성으로 선언할 수 있다.이러한 이상적인 특성을 가진 벽을 제공하는 실제 물리적 재료는 항상 쉽게 구할 수 있는 것은 아닙니다.

시스템은 보존된 양(물질 및 에너지 등) 또는 비감시된 양(엔트로피 등)이 시스템에 드나들 수 있는 벽 또는 경계로 구분됩니다.열역학 시스템 외부의 공간은 주변, 저장고 또는 환경으로 알려져 있습니다.벽의 특성에 따라 어떤 전송이 발생할 수 있는지 결정됩니다.양을 전달할 수 있는 벽은 투과성이 있다고 하며, 열역학계는 여러 벽의 투과성으로 분류된다.시스템과 주변 환경 간의 전달은 열 전도와 같은 접촉이나 주변의 전장과 같은 장거리 힘에 의해 발생할 수 있습니다.

모든 전송을 막는 벽이 있는 시스템은 격리되어 있다고 합니다.이것은 이상적인 개념입니다.실제로 어떤 전달은 항상 가능하기 때문입니다.예를 들어 중력에 의한 전달입니다.고립된 시스템이 시간과 함께 더 이상 상태가 변하지 않을 때 결국 내부 열역학적 평형에 도달하는 것은 열역학 공리입니다.

닫힌 시스템의 벽은 열과 일처럼 에너지를 전달할 수 있지만 물질적으로는 그렇지 않습니다.열린 시스템의 벽은 물질과 에너지의 ^{[13][14][15][16][17][18][19]}전달을 가능하게 한다.이 용어 정의 체계는 어떤 목적에는 편리하지만 균일하게 사용되지 않는다.특히, 일부 작가들은 '분리된 시스템'을 사용하는 '^[20][21]폐쇄 시스템'을 사용한다.

경계를 넘어 시스템의 내용 변화에 영향을 미치는 모든 것은 적절한 균형 방정식으로 설명해야 한다.부피는 1900년에 정의된 Max Planck와 같이 단일 원자 공명 에너지를 둘러싼 영역일 수 있으며, 1824년에 정의된 Sadi Carnot과 같은 증기 엔진 내의 증기 또는 공기의 본체가 될 수 있습니다.또한 양자 열역학에서 가설화된 하나의 핵종(즉, 쿼크 시스템)일 수도 있습니다.

주변 환경

시스템은 연구되고 있는 우주의 일부인 반면, 주변 환경은 시스템의 경계 밖에 있는 우주의 나머지 부분입니다.환경 또는 저수지로도 알려져 있습니다.시스템의 종류에 따라 질량, 에너지(열 및 작업 포함), 운동량, 전하 또는 기타 보존 특성을 교환하여 시스템과 상호 작용할 수 있습니다.이러한 상호 작용에 관한 경우를 제외하고, 시스템 분석에서는 환경이 무시됩니다.

폐쇄형 시스템

폐쇄형 시스템에서는 시스템 경계에서 또는 시스템 경계 밖으로 질량을 전송할 수 없습니다.시스템에는 항상 같은 양의 물질이 포함되어 있지만 (감지 가능한) 열과 (경계) 작업을 시스템의 경계를 넘어 교환할 수 있습니다.시스템이 열을 교환할 수 있는지, 작업할 수 있는지 또는 둘 다 교환할 수 있는지 여부는 해당 경계 속성에 따라 달라집니다.

• 단열 경계 – 열 교환 금지:열적으로 격리된 시스템
• 견고한 경계 – 작업 교환 금지: 기계적으로 격리된 시스템

실린더 내의 피스톤에 의해 오일이 압축되는 것이 한 예입니다.폐쇄 시스템의 또 다른 예는 폭탄 열량계입니다. 폭탄 열량계는 특정 반응의 연소 열을 측정하는 데 사용되는 정용량 열량계의 한 종류입니다.전기에너지는 경계를 넘어 전극 사이에 불꽃을 만들어 내고 연소를 시작합니다.열 전달은 연소 후 경계를 넘어 발생하지만 어느 쪽으로든 질량 전달은 이루어지지 않습니다.

닫힌 시스템의 에너지 전달을 위한 열역학 제1법칙은 다음과 같습니다.

${\displaystyle\Delta U=Q-W}$

$여기$서 U$\displaystyle$U는 시스템의$$ 내부$$ $에너지{\displaystyle }$, Q$\displaystyle$ Q$\$displaystyle W$\displaystyle$ W는 시스템에$$ 추가된 열을 $나타냅니다{\displaystyle }$.미미한 변경에 대해서는 닫힌 시스템의 제1법칙에 다음과 같이 기술할 수 있습니다.

${\displaystyle \mathrm {d} U=\delta Q-\delta W}$

작업이 $압력{\displaystyle }$P$(\displaystyle$ P$)$에서 ${\displaystyle d}$ V$(\$displaystyle \$mathrm$ {$d} V)$의 볼륨$$ 확장에 의한 경우:

$(\displaystyle \displaystyle W=P\mathrm {d}V)$

준역성 열전달의 경우 열역학 제2법칙은 다음과 같습니다.

$\displaystyle \display Q=T\mathrm {d} S}$

$여기$서 T$(\displaystyle$ T$)$는 시스템의 열역학적 온도를 $나타내고{\displaystyle }$S(\$displaystyle$S)는$$ 시스템의 엔트로피를 나타냅니다.이러한 관계에서 내부 에너지의 변화를 계산하는 데 사용되는 기본적인 열역학 관계는 다음과 같이 표현됩니다.

$\displaystyle \mathrm {d} U=T\mathrm {d} S-P\mathrm {d} V$

하나의 입자(원자 또는 분자)만 있는 단순한 시스템의 경우 닫힌 시스템은 일정한 수의 입자에 해당합니다.화학반응을 하는 시스템의 경우, 반응 과정에 의해 생성되고 파괴되는 모든 종류의 분자가 있을 수 있습니다.이 경우, 시스템이 닫혀 있다는 사실은 분자 종류에 관계없이 각 원소 원자의 총수가 보존되어 있음을 나타내는 것으로 표현된다.수학적으로:

$\displaystyle \sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{0}$

${\displaystyle {여기}_{}}$서 N$$j(\$displaystyle N_{j})$는 j$(\displaystyle$j)형$$ $분자수{\displaystyle }$${\displaystyle {}_{}}$, $(\$$displaystyle$ $a_{ij})$는 j$(\displaystyle$$$j$)$의 $,$ ${\displaystyle {\mathrm{}}_{}^{}}$ 0$(\$은$$i원소의 총 원자수입니다.$\displaystyle$ i$}$는 시스템이 닫혀 있기 때문에 일정하게 유지됩니다.시스템의 각 요소에는 이러한 방정식이 하나씩 있습니다.

격리 시스템

고립된 시스템은 어떤 방식으로든 주변과 상호작용하지 않기 때문에 폐쇄된 시스템보다 더 제한적입니다.질량과 에너지는 시스템 내에서 일정하게 유지되며 경계를 넘어서는 에너지나 질량 전달은 이루어지지 않습니다.고립된 시스템에서는 시간이 경과함에 따라 시스템 내부의 차이가 균등해지고 압력과 온도가 균등해지는 경향이 있으며 밀도 차이도 마찬가지입니다.모든 균등화 과정이 실질적으로 완료된 시스템은 열역학적 평형 상태에 있다.

예를 들어 질량과 ^{[22][23][24][25][26]}질량을 가진 시스템 사이에는 항상 중력이 존재하기 때문에 진정으로 고립된 물리적 시스템은 현실에는 존재하지 않습니다(아마도 우주 전체는 제외).그러나 실제 시스템은 한정된 시간(아마도 매우 긴 시간) 동안 거의 고립된 시스템처럼 동작할 수 있습니다.고립된 시스템의 개념은 많은 실제 상황을 근사하는 유용한 모델로 작용할 수 있습니다.이것은 특정 자연 현상의 수학적 모델을 구성하는 데 사용되는 허용 가능한 이상화입니다.

열역학 제2법칙에서 엔트로피 증가의 전제를 정당화하기 위해 볼츠만의 H-이론은 시스템(예를 들어 기체)이 분리되었다고 가정하는 방정식을 사용했다.이것이 모든 기계적 자유도를 지정할 수 있으며, 벽을 단순히 거울 경계 조건으로 취급합니다.이것은 필연적으로 로슈미트의 역설로 이어졌다.그러나 주변 배경 열복사의 무작위화 효과와 함께 실제 벽에서 분자의 확률적 거동을 고려한다면 볼츠만의 분자 혼돈 가정이 정당화될 수 있다.

고립된 시스템에 대한 열역학 제2법칙은 평형 상태에 있지 않은 고립된 시스템의 엔트로피가 시간이 지남에 따라 증가하여 평형 상태에 있는 최대값에 근접하는 경향이 있다고 말합니다.전체적으로 고립된 시스템에서는 내부 에너지가 일정하고 엔트로피가 절대 감소하지 않습니다.닫힌 시스템의 엔트로피는 예를 들어 시스템에서 열을 추출할 때 감소할 수 있습니다.

격리된 시스템은 폐쇄된 시스템과 동등하지 않다는 점에 유의해야 합니다.닫힌 시스템은 주변과 물질을 교환할 수 없지만 에너지를 교환할 수 있다.고립된 시스템은 물질도 에너지도 주변과 교환할 수 없으며, 따라서 이론적인 것일 뿐 현실에는 존재하지 않는다.

'폐쇄 시스템'은 '고립 시스템'이 정확할 때 열역학 논의에서 자주 사용된다. 즉, 에너지가 시스템에 들어오거나 나오지 않는다는 가정이 있다.

물질의 선택적 이전

열역학 프로세스에서는 가능한 프로세스를 결정하기 때문에 시스템 벽과 주변의 정확한 물리적 특성이 중요합니다.

개방형 시스템은 물질의 전달을 허용하는 하나 또는 여러 개의 벽을 가지고 있습니다.개방형 시스템의 내부 에너지를 고려하기 위해서는 열 및 작업에 대한 조건 외에 에너지 전달 조건이 필요합니다.그것은 또한 화학적 잠재력에 대한 개념으로 이어집니다.

순수 물질만을 선택적으로 투과할 수 있는 벽은 시스템을 그 순수 물질의 주변 저장소와 확산 접촉시킬 수 있다.그러면 그 순수한 물질이 시스템과 주변 환경 사이에 전달되는 과정이 가능하다.또, 그 벽을 넘어, 그 물질에 대한 접촉 평형이 가능하다.적절한 열역학적 연산에 의해 순물질 저장고는 폐쇄계로서 취급할 수 있다.내부 에너지와 엔트로피는 온도, 압력, 몰 수 함수로 결정될 수 있다.

열역학적 연산은 그 물질의 접촉 평형벽 이외의 모든 시스템벽을 불침투로 만들 수 있다.이를 통해 해당 물질에 대한 주변 환경의 기준 상태와 관련하여 강도 높은 상태 변수를 정의할 수 있다.집중 변수는 화학 퍼텐셜이라고 불리며 성분 물질 i의 경우 일반적으로 μ로_i 표시됩니다.해당하는 광범위한 변수는 시스템 내 성분 물질의 몰 N_i 수일 수 있습니다.

어떤 물질에 투과할 수 있는 벽을 가로지르는 접촉 평형의 경우, 그 물질의 화학적 전위는 벽의 양쪽에서 동일해야 한다.이것은 열역학 평형의 성질의 일부이며 열역학 ^[27]제0법칙과 관련이 있다고 볼 수 있다.

오픈 시스템

이 섹션은 확장해야 합니다.추가하시면 됩니다. (2016년 9월)

개방형 시스템에서는 시스템과 주변 환경 간에 에너지와 물질이 교환됩니다.개방형 비커에 반응물이 있는 것은 개방형 시스템의 한 예입니다.여기서 경계는 비커와 반응물을 둘러싼 가상의 표면이다.물질의 경계선이 뚫릴 수 없는 경우에는 폐쇄라고 이름 붙여지지만, 열의 형태로 에너지가 전달되도록 하고, 열과 물질의 교환이 없는 경우에는 분리한다.열린 시스템은 평형 상태에서 존재할 수 없습니다.평형에서 열역학계의 편차를 설명하기 위해 앞에서 설명한 구성 변수 외에 내부 변수 ${\displaystyle {11\mathrm{}}_{}}$ ${\displaystyle {22\mathrm{}}_{}}$ $...(\displaystyle \xi$ _${1},\xi$ _${2},\ldots})$가 도입되었다.평형 상태는 안정된 것으로 간주됩니다.그리고 내부 변수의 주요 특성은 시스템의 비평형 척도로서 사라지는 경향이다; 소멸의 국소 법칙은 각 내부 변수에 대한 완화 방정식으로 쓰여질 수 있다.

$({displaystyle {d\xi _{i}}{dt}}=-{\frac {1}{i}},\left(\xi _{i}-\xi _{i}^{(0)}\오른쪽),\flac i=1,2,\ldots,$

(1)

$여기$서 ${\displaystyle i_{}}$ i ${\displaystyle {}_{}}$ ${\displaystyle {\tau }_{}}$i ( ${\displaystyle T}$, ${\displaystyle {}_{}{}_{}{}_{}}$ ,${\displaystyle {}_{}{x\mathrm{}}_{}}$ 2${\displaystyle }$, ${\displaystyle ...{}_{}}$,$$x ${\displaystyle n_{}}$ ) { $displaystyle$\$displaystyle$ _ ${$i} = \ $displays$ _ { $i$} ($T$, $x$_ {1$}$ , x$_$ {2} , $\ldots$, x _ { n$$} )는$$ 대응하는 변수의 완화 시간입니다.초기값 ${\displaystyle {\theta }_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 0$(\$ _${i}^0})$은 0이라고 생각하면 편리합니다.

개방된 비균형 시스템의 열역학에 대한 구체적인 기여는 화학 반응 ^[28]물질 시스템을 연구한 일리야 프리고긴에 의해 이루어졌다.이 경우 내부 변수는 화학반응의 불완전성을 측정하는 것으로 보인다. 즉, 화학반응이 있는 것으로 간주되는 시스템이 얼마나 평형을 벗어났는지에 대한 측정값이다.이 이론은 시스템의 구조, 온도 경사, 물질의 농도 차이 등 평형 상태로부터의 편차를 고려하도록 일반화할 ^[29][30][31]수 있으며, 모든 화학 반응의 완전도는 말할 것도 없고 내부 변수이다.

T ${\displaystyle =}$ ${\displaystyle c}$ ${\displaystyle \mathrm{on}}$ s $t${ $displaystyle$ T$=const}$ 및$$ $p{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle c}$ ${\displaystyle \mathrm{on}}$ ${\displaystyle s}$ t$${ $displaystyle$ p$=const}$에서 깁스 자유 $에너지{\displaystyle }$G(\$displaystyle$ G$)$ 및 $엔트로피{\displaystyle }$S(\$displaystyle$ S$)$의 증분은 다음과 같이 결정된다.

${\displaystyle dG=\sum _{j},\Xi _{j},\Delta \xi _{j}+\sum _{\alpha},\mu _{\alpha},\Delta N_{\alpha }}}$

(2)

$\displaystyle T,dS=\Delta Q-\sum _{j},\Xi _{j},\Delta \xi _{j}+\sum _{\alpha },\eta _{\alpha },\Delta N_{\alpha }.$

(3)

시스템의 정지 상태는 열 에너지 ${\displaystyle {}_{}}$ $(\$와 입자 스트림의 교환으로 인해 존재합니다.마지막 항의 합계는 양수 또는 음수일 수 있는 물질 입자의 ${\displaystyle {}_{}}$ δ N$$(\$displaystyle$ \$Delta N_${\alpha$$})와$$ 함께 시스템에 들어오는 총 에너지를 나타낸다. $(\$ _${\alpha })$는 $물질{\displaystyle }$α(\$displaystyle \alpha$의 화학적 잠재력이다.식 (2)와 (3)의 중간항은 내부변수 ${\displaystyle j_{}}$j {\$displaystyle$ \$xi$ _${j$의 이완에 의한 에너지 소산(엔트로피 생산)을 나타내며, ${\displaystyle {\xi }_{}}$ j$${\$displaystyle \Xi$ _${j}$는 열역학적 힘이다.

개방 시스템에 대한 이러한 접근은 열역학적 ^[32]관점에서 살아있는 물체의 성장과 발달을 설명할 수 있게 해줍니다.

「 」를 참조해 주세요.

• 동적 시스템
• 에너지 시스템
• 격리 시스템
• 기계 시스템
• 물리 시스템
• 양자계
• 열역학 사이클
• 열역학 과정
• 2상태 양자계

레퍼런스

원천

• Abbott, M.M.; van Hess, H.G. (1989). Thermodynamics with Chemical Applications (2nd ed.). McGraw Hill.
• 캘런, H.B.(1960/1985년)열역학 및 온도조절개론, (1960년 제1판) 1985년 제2판, 뉴욕, Wiley, ISBN 0-471-86256-8.
• Halliday, David; Resnick, Robert; Walker, Jearl (2008). Fundamentals of Physics (8th ed.). Wiley.
• Moran, Michael J.; Shapiro, Howard N. (2008). Fundamentals of Engineering Thermodynamics (6th ed.). Wiley.