f-번호
f-number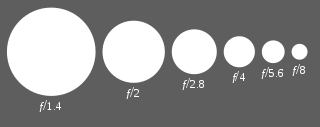
광학에서 카메라 렌즈와 같은 광학 시스템의 f-number는 입구 동공의 직경에 대한 시스템의 초점 거리의 비율입니다.[1][2][3]초점비, f-ratio, 또는 f-stop이라고도 하며 [4]사진에 매우 중요합니다.이것은 렌즈 속도의 정량적 측정값인 무차원 수치입니다. f-number가 증가하는 것을 정지라고 합니다.f-number는 일반적으로 f/N 형식의 소문자 후크 f를 사용하여 표시됩니다.여기서 N은 f-number입니다.
f-number는 상대 개구부(개구 직경을 초점 [5]거리로 나눈 값)의 역수입니다.
표기법
f-number N은 다음과 같이 지정됩니다.
서f {\f는 초점 이고 {\ D}는 입구 동공의 직경(유효 구멍)입니다.f-numbers 뒤에 f/를 쓰는 것이 관례이며, ff와 [1]으로 입구 동공 직경을 수학적으로 표현한다.예를 들어 렌즈의 초점 거리가 10mm이고 입사 동공 직경이 5mm이면 f-번호는 2가 됩니다.이것은 렌즈 시스템에서 "f/2"로 표현됩니다.조리개 직경은 f/ /2와 .
대부분의 렌즈에는 조리개 스톱의 크기와 입구 동공 크기를 변경하는 조절 가능한 다이어프램이 있습니다.이를 통해 의사는 필요에 따라 f-number를 변경할 수 있습니다.입구 동공 직경이 조리개 전면 렌즈 요소의 확대 효과 때문에 조리개 정지 직경과 반드시 동일하지는 않다는 점을 인식해야 한다.
광투과 효율의 차이를 무시하고 f-number가 큰 렌즈는 어두운 이미지를 투사합니다.렌즈의 시야(조도)에서 장면의 밝기에 대한 투영된 이미지의 밝기(조도)는 f-숫자의 제곱에 따라 감소합니다.100mm 초점 거리 f/4 렌즈는 입구 동공 직경이 25mm입니다.100 mm 초점 거리 f/2 렌즈는 입구 동공 직경이 50 mm입니다.동공 [6]직경의 제곱에 따라 면적이 달라지기 때문에 f/2 렌즈가 받아들이는 빛의 양은 f/4 렌즈의 4배입니다.동일한 사진 노출을 얻으려면 노출 시간을 4배까지 줄여야 합니다.
200mm 초점 거리 f/4 렌즈는 입구 동공 직경이 50mm입니다.200mm 렌즈의 입구 동공은 100mm f/4 렌즈 입구 동공의 4배 면적을 가지며, 따라서 렌즈의 시야에 있는 각 물체로부터 4배의 빛을 모읍니다.그러나 100mm 렌즈에 비해 200mm 렌즈는 각 물체의 2배 높낮이, 2배 넓이의 화상을 투사해, 4배의 면적을 커버하기 때문에, 소정의 휘도의 장면을 촬영할 때는, 양쪽 렌즈가 초점면에서 같은 조도를 낸다.
T-stop은 광전송 효율을 고려하여 조정된 f-번호입니다.
정지, f-stop 규칙 및 노출
stop이라는 단어는 여러 가지 의미 때문에 가끔 헷갈린다.스톱은 물리적인 물체일 수 있습니다.즉, 광학계의 불투명한 부분으로 특정 광선을 차단합니다.조리개 스톱은 입력 동공 크기를 제한하여 이미지의 밝기를 제한하는 조리개 설정이며, 필드 스톱은 원하는 시야 밖에 있는 빛을 차단하기 위한 정지이며, 정지하지 않으면 플레어 등의 문제를 일으킬 수 있습니다.
사진술에서 스톱은 빛 또는 노광의 비율을 정량화하는 데 사용되는 단위이기도 하며, 각 스톱은 2의 계수를 의미하며, 각 스톱은 2분의 1의 계수를 의미한다.원스톱 유닛은 EV(노출값) 유닛이라고도 합니다.카메라에서 조리개 설정은 전통적으로 f-stops로 알려진 개별 단계로 조정됩니다.각 "정지"는 대응하는 f-번호로 표시되며, 이전 정지로부터의 광강도의 반감을 나타낸다.이는 동공 및 조리개 직경이1/ 1 {2 또는 약 0. 감소하여 동공 면적이 절반으로 줄어드는 것에 해당합니다.
대부분의 최신 렌즈는 표준 f-stop 눈금을 사용합니다. 이는 2의 제곱근의 거듭제곱근에 해당하는 대략적인 기하학적 수열입니다: f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/11, f/16, f/22, f/32, f/45, f/64.시퀀스의 각 요소는 왼쪽 요소보다 한 정거장 낮고 오른쪽 요소보다 한 정거장 높습니다.비율의 값은 이러한 일반적인 수치로 반올림되어 기억 및 기록하기가 쉬워집니다.위의 시퀀스는 다음과 같은 정확한 기하학적 시퀀스를 근사하여 얻을 수 있습니다.
사진작가는 때때로 다른 노출 비율을 '정지'로 표현한다.f-stops는 f-number 표시를 무시하고 노출 강도의 로그 눈금을 만듭니다.이러한 해석을 고려할 때, 노출 차이를 "반쪽 정지"로 만들기 위해 이 척도를 따라 반 걸음을 내딛는 것을 생각할 수 있다.
부분 정지
대부분의 20세기 카메라는 홍채 조리개를 사용하여 연속적으로 가변적인 조리개를 가지고 있었고, 각각의 전면 정지가 표시되었다.클릭스톱 애퍼처는 1960년대에 보편적으로 사용되었습니다. 애퍼처 스케일은 보통 전체와 하프스톱마다 클릭스톱이 있었습니다.
현대의 카메라에서는, 특히 카메라 본체에 조리개가 설정되어 있을 때, f-number는 종종 한 번의 정지 단계보다 더 정교하게 분할됩니다.1/3 정지 단계(필름 속도의 ISO 시스템과 일치하기 때문에 1⁄3 EV)가 가장 일반적입니다.일부 카메라에서는 하프 스톱 스텝이 사용됩니다.일반적으로 전체 정지가 표시되고 중간 위치가 클릭됩니다.예를 들어 f/2.8보다 작은 3분의 1정지는 f/3.2, 3분의 2정지는 f/3.5, 1정지는 f/4이다.이 시퀀스의 다음 몇 가지 f-stop은 다음과 같습니다.
완전 정지(1EV)의 단계를 계산하려면 다음을 사용할 수 있습니다.
하프 스톱(1⁄2 EV) 시리즈의 스텝은 다음과 같습니다.
세 번째 정지(1⁄3 EV) 시리즈의 단계는 다음과 같습니다.
이전의 DIN 및 ASA 필름 속도 표준과 마찬가지로 ISO 속도는 1/3 정지 단위로만 정의되며, 디지털 카메라의 셔터 속도는 일반적으로 동일한 척도로 몇 초 단위로 정의됩니다.ISO 범위의 일부는 시퀀스입니다.
한편, 셔터 속도(상호 초)는, 그 숫자에 몇개의 종래의 차이가 있습니다(1µ16, 1µ32, 1µ64 대신에 1µ15, 1µ30, 1µ60초).
실제로 렌즈의 최대 조리개는 종종 θ2의 적분배수(즉, θ2의 정수승)가 아니며, 이 경우 보통 θ2의 적분배수 위 또는 아래에 반 또는 세 번째 정지한다.
SLR 카메라에 사용되는 것과 같은 최신 전자 제어식 교환 렌즈는 내부에 f-stop이 1⁄8-stop 단위로 지정되어 있기 때문에, 카메라의 1⁄3-stop 설정은 [citation needed]렌즈의 가장 가까운 1⁄8-stop 설정으로 근사합니다.
표준 풀스톱 f-번호 척도
일반 및 계산된 f-number, 풀스톱 시리즈:
| AV | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.5 | 0.7 | 1.0 | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 | 45 | 64 | 90 | 128 | 180 | 256 |
| 계산된 | 0.5 | 0.707... | 1.0 | 1.414... | 2.0 | 2.828... | 4.0 | 5.657... | 8.0 | 11.31... | 16.0 | 22.62... | 32.0 | 45.25... | 64.0 | 90.51... | 128.0 | 181.02... | 256.0 |
일반적인 반정지 f-번호 척도
| AV | −1 | -1×2 | 0 | 1/2 | 1 | 1+1/2 | 2 | 2+1/2 | 3 | 3+1/2 | 4 | 4+1/2 | 5 | 5+1/2 | 6 | 6+1/2 | 7 | 7+1/2 | 8 | 8+1/2 | 9 | 9+1/2 | 10 | 10+1/2 | 11 | 11+1/2 | 12 | 12+1/2 | 13 | 13+1/2 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 1.0 | 1.2 | 1.4 | 1.7 | 2 | 2.4 | 2.8 | 3.3 | 4 | 4.8 | 5.6 | 6.7 | 8 | 9.5 | 11 | 13 | 16 | 19 | 22 | 27 | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 107 | 128 |
일반적인 1/3 정지 f-번호 척도
| AV | −1 | -2×3 | -1×3 | 0 | 1/3 | 2×3 | 1 | 1+1/3 | 1+2×3 | 2 | 2+1/3 | 2+2×3 | 3 | 3+1/3 | 3+2×3 | 4 | 4+1/3 | 4+2×3 | 5 | 5+1/3 | 5+2×3 | 6 | 6+1/3 | 6+2×3 | 7 | 7+1/3 | 7+2×3 | 8 | 8+1/3 | 8+2×3 | 9 | 9+1/3 | 9+2×3 | 10 | 10+1/3 | 10+2×3 | 11 | 11+1/3 | 11+2×3 | 12 | 12+1/3 | 12+2×3 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 | 36 | 40 | 45 | 51 | 57 | 64 | 72 | 80 | 90 |
때로는 여러 척도에 동일한 수치가 포함될 수 있습니다. 예를 들어, f/1.2의 조리개를 하프 스톱[7] [8]또는 1/3 스톱 시스템에 사용할 수 있으며, 때로는 f/1.3과 f/3.2 및 기타 차이를 1/3 스톱 [9]척도에 사용할 수 있습니다.
일반적인 1/4 정지 f-번호 척도
| AV | 0 | 1×4 | 1/2 | 3×4 | 1 | 1+1×4 | 1+1/2 | 1+3×4 | 2 | 2+1×4 | 2+1/2 | 2+3×4 | 3 | 3+1×4 | 3+1/2 | 3+3×4 | 4 | 4+1×4 | 4+1/2 | 4+3×4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.7 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3.1 | 3.3 | 3.7 | 4 | 4.4 | 4.8 | 5.2 | 5.6 |
| AV | 5 | 5+1×4 | 5+1/2 | 5+3×4 | 6 | 6+1×4 | 6+1/2 | 6+3×4 | 7 | 7+1×4 | 7+1/2 | 7+3×4 | 8 | 8+1×4 | 8+1/2 | 8+3×4 | 9 | 9+1×4 | 9+1/2 | 9+3×4 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 5.6 | 6.2 | 6.7 | 7.3 | 8 | 8.7 | 9.5 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 |
H 스톱
H-stop(공용, 대문자 H로 표기된 규약)은 Rodenstock Imagon 렌즈에 있는 확산 디스크 또는 체 개구부의 구멍에 의해 덮인 면적에 근거해 유효 노광에 상당하는 f-수이다.
티스톱
T스톱(송신정지용, 대문자 T로 표기된 규약에 의해)은 광투과효율(투과율)을 고려하도록 조정된 f번호이다.T-stop이 N인 렌즈는 투과율이 100%이고 f-number가 N인 이상적인 렌즈와 같은 휘도의 화상을 투영한다.특정 렌즈의 T-stop, T는 f-number를 해당 렌즈의 투과율의 제곱근으로 나누어 구한다.
코팅되지 않은 렌즈의 공기 유리 표면당 손실이 8%인 렌즈의 멀티코팅은 렌즈 디자인의 핵심이다.일부 렌즈 리뷰는 벤치마크에서 [11][12]T-stop 또는 투과율을 측정합니다.특히 외부 [13]광도계를 사용할 때 노출을 보다 정확하게 판단하기 위해 f-number 대신 T-stop을 사용하는 경우가 있습니다.렌즈 투과율은 일반적으로 60%~95%[14]입니다.티스톱은 많은 영상이 연속적으로 보이고 노출의 작은 변화도 눈에 띄는 촬영에 자주 사용됩니다.시네마 카메라 렌즈는 일반적으로 f-number가 [13]아닌 T-stop으로 보정됩니다.스틸 사진에서는 사용되는 모든 렌즈와 카메라의 엄격한 일관성을 필요로 하지 않고 노출의 약간의 차이는 덜 중요하지만, T-stops는 미놀타나 소니의 Smooth Trans Focus 렌즈와 같은 특수 목적 렌즈에 여전히 사용되고 있습니다.
Sunny 16
사진에 f-number를 사용하는 예로는 sunny 16 규칙을 들 수 있습니다.예를 들어 ISO 200 필름, f/16 구멍 및 1µ200초의 셔터 속도를 사용하여 햇빛이 잘 드는 날에 대략 정확한 노출을 얻을 수 있는 것은 ISO 200 필름, f/16 구멍 및 1µ200초의 셔터 속도를 사용합니다.f-number는 조도가 낮은 상황에서는 아래쪽으로 조정할 수 있습니다.낮은 f-number를 선택하면 렌즈가 "개방"됩니다.높은 f-number를 선택하면 렌즈의 "닫기" 또는 "정지"가 됩니다.
이미지 선명도에 미치는 영향
f-number에 따라 필드의 깊이가 증가합니다(여기 그림 참조).즉, 낮은 f-number(큰 조리개)로 촬영한 사진은 피사체의 초점을 한 거리에 두고 나머지 이미지(근처 및 먼 요소)는 초점이 맞지 않는 경향이 있습니다.배경 흐림('보케'로 알려진 심미적 특성)이 미적으로 즐거울 수 있고 시청자의 주요 피사체에 대한 집중을 전경에 두기 때문에 이것은 자연 사진 및 초상화에 자주 사용됩니다.주어진 f-번호로 생성되는 이미지의 필드 깊이는 초점 거리, 피사체 거리, 이미지 캡처에 사용되는 필름 또는 센서의 형식 등 다른 파라미터에 따라 달라집니다.시야 깊이는 시야각, 피사체 거리 및 입사 동공 직경(von Rohr의 방법처럼)에 따라 설명될 수 있습니다.그 결과, 작은 포맷은 같은 초점 거리와 같은 화각에 대해 같은 f-번호의 큰 포맷보다 더 깊은 필드를 가진다.작은 포맷은 같은 화각을 생성하기 위해 더 짧은 초점 거리(와이드 각도 렌즈)를 필요로 하고, 짧은 초점 거리에 따라 더 깊은 필드(field)가 증가시키기 때문이다.따라서 축소된 심도 효과는 소형 카메라를 사용할 때 대형 카메라를 사용할 때보다 더 작은 f-number(그리고 잠재적으로 더 어렵거나 복잡한 광학)를 필요로 한다.
초점을 넘어, 이미지의 선명도는 두 가지 다른 광학 효과, 즉 불완전한 렌즈 설계로 인한 수차와 빛의 [15]파동 특성에 의한 회절의 두 가지 다른 광학 효과를 통해 f 숫자와 관련됩니다.흐릿하게 최적의 f-stop은 렌즈 디자인에 따라 달라집니다.6개 또는 7개의 원소가 있는 현대 표준 렌즈의 경우 가장 선명한 이미지가 f/5.6–f/8 경에 획득되는 경우가 많으며, 4개 원소(테사 공식)만 f/11에 멈추면 가장 선명한 이미지를 [citation needed]얻을 수 있습니다.현대식 렌즈의 많은 수의 요소들은 디자이너가 수차를 보상할 수 있게 해주며, 렌즈는 낮은 f-number에서 더 나은 사진을 보여줄 수 있게 해준다.작은 구멍에서는 전계 깊이와 수차가 개선되지만, 회절은 빛의 확산을 증가시켜 흐릿함을 유발한다.
빛 낙하도 f-stop에 민감합니다.대부분의 광각 렌즈는 큰 구멍의 가장자리에서 상당한 빛의 낙하(비그네팅)를 보입니다.
사진기자들은 "f/8 and be there"라는 속담이 있는데, 이는 기술적인 세부 사항에 대해 걱정하는 것보다 현장에 있는 것이 더 중요하다는 것을 의미합니다.실질적으로 f/8(35mm 이상 형식)은 대부분의 일광 상황에서 [16]적절한 베이스 노출을 위해 충분한 시야 깊이와 충분한 렌즈 속도를 허용한다.
사람의 눈
인간 눈의 f-number 계산은 눈의 물리적 구멍과 초점 거리를 계산하는 것을 포함한다.동공의 넓이는 6~7mm 정도로 커질 수 있으며, 이는 최대 물리적 개구부로 해석됩니다.
사람의 눈의 f-number는 매우 밝은 장소에서는 약 f/8.3에서 [17]어두운 장소에서는 약 f/2.1까지 다양하다.초점 거리를 계산하려면 눈에 있는 액체의 광 굴절 특성을 고려해야 합니다.눈을 일반 공기 주입 카메라 및 렌즈로 취급하면 초점 거리와 f-번호가 부정확해집니다.
망원경의 초점비
천문학에서 f-number는 일반적으로 N{\ N으로 표기된 초점비(또는 f-ratio)라고 합니다. 여전히 물체의 D {\ D 또는 시스템에서 조리개 정지 직경으로 나눈 값으로 정의됩니다.
초점비의 원리는 항상 동일하지만, 그 원리가 적용되는 용도는 다를 수 있다.사진에서 초점비는 초점 평면 조도(또는 영상의 단위 면적당 광출력)를 변화시키며, 전계 깊이와 같은 변수를 제어하는 데 사용됩니다.천문학에서 광학 망원경을 사용할 경우, 전계 문제의 깊이가 없으며, 총 광파워에 대한 항성 점원의 밝기는 초점 거리와 무관한 절대 개구 면적만의 함수이다.초점 거리는 기기의 시야와 접안 렌즈, 필름 플레이트 또는 CCD에 초점 평면에 표시되는 이미지의 스케일을 제어합니다.
예를 들어, SURAGY 4m 망원경은 작은 시야(약 f/16)를 가지고 있어 항성 연구에 유용합니다.LSST 8.4m 망원경은 3일에 한 번씩 하늘 전체를 덮을 것이며 매우 넓은 시야를 가지고 있다.10.3m의 짧은 초점 거리(f/1.2)는 2차 및 3차 미러, 3소자 굴절 시스템 및 능동 장착 및 [18]광학 장치를 포함하는 오류 보정 시스템에 의해 가능합니다.
카메라 방정식(G#)
카메라 방정식(G#)은 카메라 [19]렌즈의 초점 평면에 대한 카메라 센서에 도달하는 광도의 비율입니다.
여기서 θ는 렌즈의 투과 계수이며 단위는 역 스테라디안(sr−1) 단위이다.
작업용 f-number
f-number는 무한 거리 [20]물체에 대해서만 렌즈의 집광 능력을 정확하게 나타냅니다.이 제한은 일반적으로 사진촬영에서 무시되며, 사진촬영에서는 물체까지의 거리에 관계없이 f-number가 자주 사용됩니다.광학 설계에서는 물체가 렌즈에서 멀지 않은 시스템에 대한 대안이 종종 필요합니다.이 경우 동작하는 f-number가 사용됩니다.동작하는 f-numberw N은 다음과 [20]같이 지정됩니다.
여기서i N은 수정되지 않은 f-number, NA는 렌즈의 이미지 공간 숫자 개구부, {\ m은 특정 거리 떨어진 물체에 대한 렌즈 배율의 절대값, P는 동공 배율입니다.동공 확대는 거의 알려져 있지 않기 때문에 흔히 1로 가정되며, 이는 모든 대칭 렌즈에 대한 정확한 값이다.
사진술에서 이것은 초점을 더 가까이 맞출수록 렌즈의 유효 조리개가 작아져 노출이 더 어두워진다는 것을 의미합니다.작동 f-번호는 종종 사진술에서 자복 계수에 의해 렌즈 확장에 대해 보정된 f-번호로 설명됩니다.이것은 매크로 사진술에서 특히 중요하다.
역사
상대 개구도를 지정하기 위한 f-number의 체계는 19세기 후반에 몇몇 다른 개구 표기 체계와 경쟁하면서 발전했다.
상대 개구부의 원점
1867년, 서튼과 도슨은 "원점비"를 본질적으로 현대의 f-숫자의 역수로 정의했다.다음 인용문에서 "1⁄24"의 "주변비"는 f/24 f-stop에 해당하는 6인치(150mm) 대 1⁄4인치(6.4mm)의 비율로 계산됩니다.
모든 렌즈에는, 주어진 개구비(즉, 초점 거리에 대한 정지 직경의 비율)에 대응해, 그 렌즈로부터 가까운 물체의 일정한 거리가 있어, 그 사이와 무한대의 모든 물체는 동등하게 양호한 초점을 가진다.예를 들어 초점 6인치 단일 뷰 렌즈에서 1⁄4인치 정지(자세비율 24분의 1)는 렌즈로부터 20피트 사이의 거리 및 무한 거리(예를 들어 고정 별)에 있는 모든 물체의 초점이 동일하게 좋다.따라서 이 스톱을 사용할 때 20피트는 렌즈의 '초점 범위'라고 불립니다.따라서 초점 범위는 가장 가까운 물체의 거리이며, 접지 유리가 매우 먼 물체에 대해 조정될 때 초점이 잘 맞춰집니다.같은 렌즈에서는 초점범위는 사용된 다이어프램의 크기에 따라 달라지지만, 같은 개구비를 가진 다른 렌즈에서는 렌즈의 초점거리가 증가할수록 초점범위가 커집니다.'초점 비율'과 '초점 범위'라는 용어는 일반적으로 사용되지 않지만, 사진 [21]렌즈의 특성을 다룰 때 모호함과 완곡함을 방지하기 위해 사용하는 것이 매우 바람직하다.
1874년, John Henry Dallmeyer는 1 을 렌즈의 "라고 불렀습니다.
렌즈의 속도는 등가 초점에 대한 조리개의 관계 또는 비율에 따라 달라집니다.이것을 확인하기 위해서, 등가 초점을 문제의 렌즈의 실제 동작하는 조리개의 직경으로 나누고, 분자에 대해 1 또는 통일성을 갖는 분모로 지수를 적어 둡니다.따라서 직경 2인치와 초점 6인치의 렌즈의 비율을 구하려면 초점을 조리개로 나누거나 6을 2로 나누면 3이 됩니다. 즉, 1⁄3은 명암비입니다.[22]
1893년 [24]지그프리드 차프스키에 의해 널리 알려진 에른스트 아베의 정지 및 [23]동공 이론을 아직 접하지 못했지만, 달마이어는 그의 작동 조리개가 조리개의 물리적 직경과 같지 않다는 것을 알고 있었다.
그러나 실제 강도비를 구하려면 실제 작동 개구부의 직경을 확인해야 합니다.이것은 단일 렌즈의 경우, 또는 완전한 개구부와 함께 사용되는 이중 콤비네이션 렌즈의 경우, 이것들은 단지 한 쌍의 나침반이나 규칙을 필요로 한다; 그러나 이중 또는 삼중 콤비네이션 렌즈의 경우, 조합 사이에 멈춤이 삽입된 경우, 다소 더 문제가 있다; 왜냐하면 그것은 명백하기 때문이다.이 경우 사용된 정지부의 직경은 전면 조합에 의해 전달되는 실제 빛의 연필의 측정값이 아니다.이것을 확인하려면 , 멀리 있는 물체에 초점을 맞추고, 포커스 스크린을 떼어내, 미리 준비된 플레이트 대신에 판지를 삽입한 상태로 콜로디온 슬라이드로 교환합니다.이고, 현재는 어두운 방을 제거하는, 촛불이 구멍에 가까운 적용하고 켜진 조각은 전면 결합을 보이는 관찰한다. 렌즈는 문제의 특정한 정류장을 사용한다고 좋은 이 원의 직경, 주의 깊게 측정할 때는 실제로 작동하는 개구는 피이서와 판지의 중심부에 있는 작고 둥근 구멍을 내다.[22]
이 점은 1893년 [24]차프스키에 의해 더욱 강조되었다.1894년 그의 책에 대한 영어 리뷰에 따르면, "물리적 멈춤의 효과적인 구멍과 직경을 명확하게 구분할 필요가 강하게 [25]주장된다."
J. H. Dallmeyer의 아들인 망원렌즈의 발명가 Thomas Rudolphus Dallmeyer는 1899년에 [26]명암비 용어를 따랐다.
개구부 번호부여 시스템
동시에, 개구비 또는 강도비의 f-number의 제곱 또는 역제곱이 아닌, 노광 시간을 개구부에 정비례 또는 반비례하도록 하기 위해 설계된 다수의 개구부 번호 부여 시스템이 있었다.그러나 이러한 시스템은 초점 거리와 직경의 단순한 비율과는 달리 임의의 상수를 포함했습니다.
예를 들어, 1880년대에 영국 사진 협회에 의해 균일한 개구부 시스템(U.S.)이 표준으로 채택되었습니다.Bothamley 1891년에 "모든 최고의 제작자들의 정류장 지금 이 시스템에 따라 배열되어 있다고 말했다.f/16로 "[27]미국 16일이 같은 개구부지만거나 작은 미국 번호를 전면 중단 사용 두배로 증가하거나 축소하는 것에 의해 큰 개구부 예를 들어 f/11은 미국 8과 f/8은 미국 4. 그 노출 시간 필요한 바로 미국으로 정비례한다.이스트만 코닥은 적어도 1920년대에 많은 카메라에서 미국식 스톱을 사용했다.
1895년까지, 호지스는 F-숫자 체계가 계승되었다고 말하면서, 보텀리에 반박한다: "이것은 f/x 체계라고 불리고, 좋은 구조의 모든 현대 렌즈들의 다이아프램은 [28]매우 두드러진다."
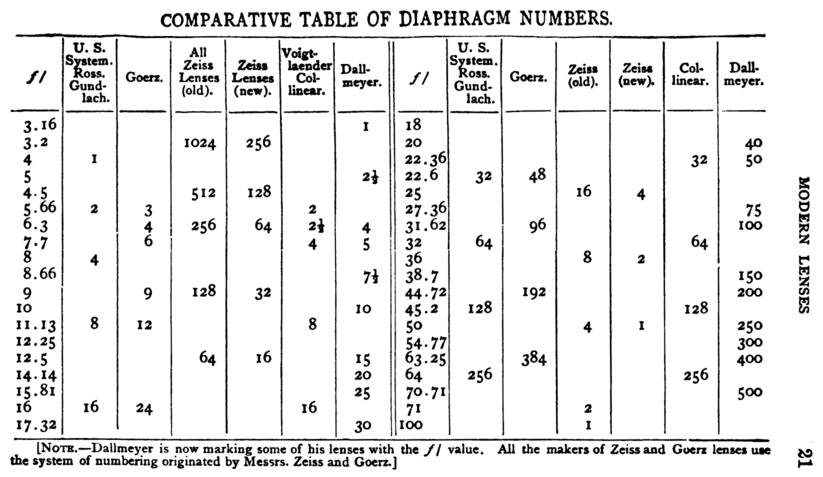
1899년의 상황을 다음에 나타냅니다.
1901년[29] Piper는 5가지 조리개 표시 시스템에 대해 논의했습니다.실제 강도에 기초한 구형 및 신형 Zeiss 시스템(f-number의 역제곱에 비례함), 노출에 기초한 미국, C.I 및 Dallmeyer 시스템(f-number의 제곱에 비례함)입니다.그는 f-숫자를 "비율수", "자세비율수", "비율 개구부"라고 부릅니다.그는 f/8과 같은 표현은 말 그대로 그가 다른 용어로 구별하는 "절대 직경"과 동일함에도 불구하고 조리개의 "절대 직경"이라고 부릅니다.그는 또한 때때로 슬래시로 구분되지 않은 "f 8의 개구부"와 같은 표현을 사용합니다.
1902년 Beck와 Andrews는 Royal Photographic Society의 f/4, f/5.6, f/8, f/11.3 [30]등에 대해 이야기합니다.R.P.S.는 1895년과 1902년 사이에 그들의 이름을 바꾸고 미국 체제를 떠났다.
인쇄 표준화

1920년까지, f-number라는 용어는 F 번호와 f/number 둘 다로 책에 등장했습니다.현대 출판물에서는 이전 형식과 F-번호가 여전히 몇 권의 책에 있지만 f-number 및 f-number 형식이 더 일반적이다. f-number 또는 f/number의 첫 번째 소문자 f는 후크 이탤릭체로 설정되어 있다.[31]
20세기 초반에는 f-number에 대한 표기법도 상당히 다양했다.대문자 F,[32] 슬래시 [33]대신 점( 마침표)으로 쓰이기도 하고 수직 분수로 [34]설정되기도 합니다.
1961년 ASA 표준 PH2.12-1961 미국 표준 범용 사진 노출계(Photo-Purpose Photographic Exposure Meter, Photo Electric Type)는 "상대 개구부의 기호는 // 또는 :: 뒤에 유효 --숫자가 이어져야 한다"고 명시하고 있다.기호뿐만 아니라 f-number에서도 갈고리 모양의 이탤릭체 '''이 나오는데, 오늘날에는 보통 비이탈릭체로 설정되어 있습니다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b Smith, Warren Modern Optical Engineering, 2007년 4월 4일 McGrow-Hill Professional, 페이지 183.
- ^ Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. p. 152. ISBN 0-201-11609-X.
- ^ Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. Bellingham, Wash: SPIE. p. 29. ISBN 9780819452948. OCLC 53896720.
- ^ Smith, Warren Modern Lens Design 2005 McGraw-Hill.
- ^ ISO, 사진—사진 렌즈와 관련된 주의사항 및 관련 특성: 지정 및 측정, ISO 517:2008
- ^ 원의 면적을 참조하십시오.
- ^ Harry C. Box (2003). Set lighting technician's handbook: film lighting equipment, practice, and electrical distribution (3rd ed.). Focal Press. ISBN 978-0-240-80495-8.
- ^ Paul Kay (2003). Underwater photography. Guild of Master Craftsman. ISBN 978-1-86108-322-7.
- ^ David W. Samuelson (1998). Manual for cinematographers (2nd ed.). Focal Press. ISBN 978-0-240-51480-2.
- ^ 투과, 광투과, DxOMark
- ^ 시그마 85mm F1.4 아트 렌즈 리뷰: 새로운 벤치마크, DxOMark
- ^ 쌍안경 및 렌즈로 렌더링 - 색상 및 전송, LensTip.com
- ^ a b "Kodak Motion Picture Camera Films". Eastman Kodak. November 2000. Archived from the original on 2002-10-02. Retrieved 2007-09-02.
- ^ Marianne Oelund, "Lens T-stops", dpreview.com, 2009
- ^ Michael John Langford (2000). Basic Photography. Focal Press. ISBN 0-240-51592-7.
- ^ Levy, Michael (2001). Selecting and Using Classic Cameras: A User's Guide to Evaluating Features, Condition & Usability of Classic Cameras. Amherst Media, Inc. p. 163. ISBN 978-1-58428-054-5.
- ^ Hecht, Eugene (1987). Optics (2nd ed.). Addison Wesley. ISBN 0-201-11609-X. 제5.7.1장
- ^ Charles F. Claver; et al. (2007-03-19). "LSST Reference Design" (PDF). LSST Corporation: 45–50. Archived from the original (PDF) on 2009-03-06. Retrieved 2011-01-10.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ Driggers, Ronald G. (2003). Encyclopedia of Optical Engineering: Pho-Z, pages 2049-3050. CRC Press. ISBN 978-0-8247-4252-2. Retrieved 2020-06-18.
- ^ a b Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. ISBN 0-8194-5294-7. 페이지 29.
- ^ 토마스 서튼과 조지 도슨, 런던 사진 사전: 샘프슨 로우, 아들 & 마스턴, 1867년 (p.12).
- ^ a b John Henry Dallmeyer, Photographic Lens: On The Choice and Use – Special Edited for American Photographist, 팸플릿, 1874.
- ^ Southall, James Powell Cocke (1910). "The principles and methods of geometrical optics: Especially as applied to the theory of optical instruments". Macmillan: 537.
theory-of-stops.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b 지그프리드 차프스키, Theorie der optischen Instrumente, 나흐 아브, 브레슬라우:트류엔트, 1893년
- ^ 헨리 크루, 천문학 및 우주물리학 XIII, 1894년 "차프스키 박사의 광학 기기 이론"
- ^ 토마스 R.Dallmeyer, Telephotography: 런던, Telephotography 렌즈의 구조와 적용에 관한 기초 논문:하이네만, 1899년
- ^ C. H. Bothamley, Ilford Manual of Photography, 런던: Britannia Works Co., 1891.
- ^ John A. Hodges, 사진 렌즈: 선택방법 및 사용방법, Bradford: Percy Lund & Co., 1895.
- ^ C. Welborne Piper, A First Book of the Lens: 사진 렌즈의 작용과 사용에 관한 기초 논문, 런던: Hazell, Watson, and Viney, 1901.
- ^ 콘래드 벡과 허버트 앤드루스, 사진 렌즈: 심플한 논문, 제2판, 런던: R. & J. Beck Ltd., c. 1902.
- ^ 구글 검색
- ^ Ives, Herbert Eugene (1920). Airplane Photography (Google). Philadelphia: J. B. Lippincott. p. 61. ISBN 9780598722225. Retrieved 2007-03-12.
- ^ Mees, Charles Edward Kenneth (1920). The Fundamentals of Photography. Eastman Kodak. p. 28. Retrieved 2007-03-12.
- ^ Derr, Louis (1906). Photography for Students of Physics and Chemistry (Google). London: Macmillan. p. 83. Retrieved 2007-03-12.

























 특정 거리 떨어진 물체에 대한 렌즈
특정 거리 떨어진 물체에 대한 렌즈