숫자 개구부

광학에서 광학 시스템의 숫자 개구(NA)는 시스템이 빛을 받아들이거나 방출할 수 있는 각도 범위를 특징짓는 무차원 수치입니다.NA는 굴절률을 정의에 포함시킴으로써 계면에 굴절력이 없는 한 빔이 한 물질에서 다른 물질로 이동할 때 일정하다는 특성을 가집니다.이 용어의 정확한 정의는 광학 분야마다 조금씩 다릅니다.숫자 개구부는 현미경 검사에서 일반적으로 물체의 수용 콘(그리고 광 채집 능력과 분해능)을 기술하기 위해 사용되며, 광섬유에서는 광섬유에 입사하는 빛이 광선을 따라 투과되는 각도 범위를 기술합니다.

일반광학

광학, 특히 현미경의 대부분의 영역에서 대물렌즈와 같은 광학계의 수치 개구부는 다음과 같이 정의된다.

$\displaystyle \mathrm {NA} = n\sin \theta , }$

여기서 n은 렌즈가 작동하는 매체의 굴절률(공기의 경우 1.00, 순수한 물의 경우 1.33, 그리고 일반적으로 ^[1]침지유의 경우 1.52)이며, θ는 렌즈에 들어오거나 나올 수 있는 빛의 원뿔의 최대 반각도이다.일반적으로, 이것은 시스템의 실제 한계선의 각도입니다.굴절률을 포함하기 때문에 광선연필이 평탄한 표면을 통과하기 때문에 광선연필의 NA는 불변성이 된다.이것은 Snell의 법칙을 재배치하여 n sin θ가 인터페이스 전체에서 일정하다는 것을 알아냄으로써 쉽게 알 수 있습니다.

공기 중 렌즈의 각도 개구부는 (근축 근사치 내) 이 값의 약 2배입니다.NA는 일반적으로 특정 물체 또는 영상 지점에 대해 측정되며 해당 지점이 이동함에 따라 달라집니다.현미경 검사에서 NA는 달리 언급하지 않는 한 일반적으로 물체 공간 NA를 가리킨다.

현미경 검사에서 NA는 렌즈의 분해력을 나타내기 때문에 중요합니다.가장 훌륭한 자세한 내용들은(이 결의안)해결될 수 있는 크기 .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{.mw-parser-output에 비례한다.디스플레이:블록, line-height:1em, 마진:00.1em}은 빛의 λ은 파장.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}λ/2NA.숫자 조리개가 큰 렌즈는 숫자 조리개가 작은 렌즈보다 세밀한 디테일을 시각화할 수 있습니다.고품질(회절제한) 광학을 가정할 때, 큰 수치구경을 가진 렌즈는 더 많은 빛을 모으며 일반적으로 더 밝은 이미지를 제공하지만, 더 낮은 시야 깊이를 제공합니다.

숫자 개구부는 광학 디스크 형식의 "^[2]피트 크기"를 정의하는 데 사용됩니다.

물체의 배율과 수치 개구부를 증가시키면 작업 거리, 즉 전면 렌즈와 표본 사이의 거리가 감소합니다.

숫자 개구부 대 f-숫자

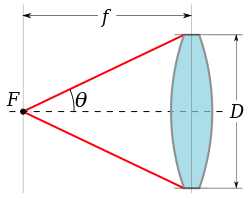
사진 촬영에는 일반적으로 숫자 조리개가 사용되지 않습니다.대신 렌즈(또는 이미징 미러)의 각도 개구부는 f/ 또는 N으로 표기된 f-number로 표현됩니다. f는 입구 동공 D의 직경에 대한 초점 거리 f의 비율로 정의됩니다.

${\displaystyle N=syslogfrac {f}{D}}.}$

이 비율은 렌즈가 ^[3]무한대에 초점을 맞출 때 영상 공간 숫자 구멍과 관련이 있습니다.오른쪽의 도표에 근거해, 렌즈의 화상 공간 수치 개구부는 다음과 같습니다.

$디스플레이 스타일NA}}_{\text{i}}=n\sin \theta =n\sin \left [\arctan \left\frac {D}{2f}\right]\apprough n'frac {D}{2f}}},$

따라서 N ≤ 1/2NA_i, 공기 중 정상 사용 가정(n = 1)

이 근사치는 수치 개구부가 작을 때 유지되지만 카메라 렌즈와 같이 잘 보정된 광학 시스템의 경우 더 자세한 분석 결과 N은 거의 정확히 1/2과 같습니다.NA는 큰 수치 개구에서도 마찬가지입니다_i.Rudolf Kingslake가 설명하듯이, "비[D/2f]가 실제로는 sin이 아니라 tan θ와 같다고 가정하는 것은 일반적인 오류입니다.물론 주 평면이 실제로 평면이라면 접선은 정확할 것입니다.그러나 아베 사인 조건의 완전한 이론은 모든 양호한 사진 목표가 그렇듯이 혼수 및 구면 수차에 대해 렌즈를 보정하면 두 번째 주평면이 초점을 중심으로 반지름 f 구체의 일부가 된다는 것을 보여준다."^[4]그런 의미에서 f-number의 전통적인 박렌즈 정의와 그림은 오해의 소지가 있으며, 이를 수치적 조리개 측면에서 정의하는 것이 더 의미가 있을 수 있다.

작업(유효) f-번호

f-number는 물체 측의 주변 광선이 렌즈의 축과 평행한 경우 렌즈의 집광 능력을 나타냅니다.이 경우는 사진 촬영에서 흔히 볼 수 있는데, 사진 촬영 대상 물체는 카메라에서 멀리 떨어져 있는 경우가 많습니다.그러나 물체가 렌즈에서 멀리 떨어져 있지 않으면 렌즈의 초점 평면에서 이미지가 형성되지 않으며, f-숫자는 렌즈의 집광 능력이나 이미지 측 개구부를 정확하게 나타내지 않습니다.이 경우, 숫자 개구부는 때때로 "작동 f-번호" 또는 "유효 f-번호"라고 불리는 것과 관련이 있습니다.

동작하는 f-number는 객체에서 이미지로의 배율을 고려하여 위의 관계를 수정함으로써 정의됩니다.

${\displaystyle\frac{1}{2개의 텍스트}NA}}_{\text{i}}}=N_{\text{w}}=\left(1-{\frac {m}{P}}\right)N,}$

여기서_w N은 작동 f-번호, m은 특정 거리 떨어진 물체에 대한 렌즈의 확대, P는 동공 확대,^[3][5] NA는 이전과 같이 주변 광선의 각도로 정의된다.여기서의 배율은 일반적으로 음수이며, 동공 배율은 앨런 R과 같이 1로 가정되는 경우가 많습니다.그린리프는 "조명도는 렌즈의 동공 출구와 플레이트 또는 필름 위치 사이의 거리의 제곱에 따라 반대 방향으로 변화한다"라고 설명합니다.출구 동공의 위치는 보통 렌즈의 사용자가 알 수 없기 때문에 후방 공역 초점 거리가 대신 사용됩니다. 이렇게 도입된 이론적 오류는 대부분의 유형의 사진 ^[6]렌즈에서 중요하지 않습니다."

사진술에서 계수는 1 + m으로 기록되기도 합니다. 여기서 m은 배율의 절대값을 나타냅니다. 두 경우 모두 보정 계수는 1 이상입니다.위의 방정식의 두 등식은 인용된 출처가 나타내듯이, 다양한 저자에 의해 각각 작동 f-번호의 정의로 받아들여진다.둘 다 꼭 정확한 것은 아니지만 종종 그런 것처럼 취급됩니다.

반대로, 물체 측 숫자 개구부는 배율을 통해 f-숫자와 관련된다(멀리 있는 물체의 경우 0이 되는 경향이 있다).

${\displaystyle\frac{1}{2개의 텍스트}NA}}_{\text{o}}}=440frac {m-P}{mP}}N.}$

레이저 물리학

레이저 물리학에서 숫자 개구부는 약간 다르게 정의됩니다.레이저 광선은 전파되면서 천천히 퍼집니다.빔의 가장 좁은 부분으로부터 멀리 떨어져 있는 경우, 확산은 거리에 따라 대략적으로 선형이며, 레이저 빔은 "원거리 필드"에서 빛의 원뿔을 형성합니다.레이저 빔의 NA를 정의하는 데 사용되는 관계는 광학 시스템에 사용되는 것과 동일합니다.

$디스플레이 스타일NA}}=n\sin \theta,}$

θ는 다르게 정의되어 있습니다.레이저 빔은 일반적으로 렌즈의 구멍을 통과하는 빛의 원뿔처럼 날카로운 모서리를 가지고 있지 않습니다.대신 빔의 중심에서 점차적으로 방사 조도가 떨어집니다.빔이 가우스 프로파일을 갖는 것은 매우 일반적입니다.레이저 물리학자들은 일반적으로 빔의 발산, 즉 빔 축과 빔 조도가 떨어지는 축으로부터의 거리 사이의 원거리 각도에서⁻² e배 온 축 방사선 조도를 선택하게 된다.가우스 레이저 빔의 NA는 그 최소 스폿 크기("빔 웨이스트")와 관련지어집니다.

$디스플레이 스타일NA}}\simeq {frac {lambda _ {0}}{\pi w_{0}}}$

여기서 θ는₀ 빛의 진공 파장이고, 2w는₀ 가장 좁은 지점의 빔 직경이며, e⁻² 방사 조도 지점 사이에서 측정된("e 최대 강도의⁻² 전폭")입니다.즉, 작은 점에 초점을 맞춘 레이저 빔은 초점으로부터 멀어질 때 빠르게 퍼지는 반면, 큰 직경의 레이저 빔은 매우 먼 거리에 걸쳐 거의 같은 크기를 유지할 수 있습니다.참고 항목: 가우스 빔 폭

광섬유

멀티 모드 광섬유는 파이버의 Acception con이라고 불리는 일정한 각도 범위 내에서 파이버에 입사하는 빛만 전파합니다.이 원뿔의 반각도를 수용각도 θ라고_max 합니다.특정 매체의 스텝 인덱스 멀티 모드 파이버의 경우, 수용 각도는 코어, 클래드 및 매체의 굴절률로만 결정됩니다.

${\displaystyle n\sin \theta _{\max }=sargrt {n_{\text{core}^2}-n_{\text{clad}^2}}}$

여기서 n은 섬유 주변 매체의 굴절률, n은_core 섬유 코어의 굴절률, n은_clad 피복재의 굴절률이다.코어는 더 높은 각도의 빛을 받아들이지만, 이러한 광선은 코어의 피복 인터페이스에서 완전히 반사되지 않기 때문에 파이버의 다른 쪽 끝으로 전송되지 않습니다.이 공식의 도출은 다음과 같다.

광선이 굴절률 n의 매질에서 최대 수용각 n의 핵심으로_core 입사할 때, 중간 코어 계면에서 스넬의 법칙은 다음을 나타낸다.

$\displaystyle n\sin \theta _{\max }=n_{\text{core}}\sin \theta _{r}.\ }$

위 그림의 지오메트리에서 얻은 것은 다음과 같습니다.

${\displaystyle \sin \theta _{r}=\sin \leftsheta90^{\sin}}-\theta _{c}=\cos \theta _{c}}$

어디에

$\displaystyle \theta _{c}=\arcsin {frac {n_{\text{core}}{n_{\text{core}}}$

전체 내부 반사에 대한 임계 각도입니다.

스넬의 법칙에서 죄 대신 cos for로_cr 치환하면 다음과 같은 결과가 나옵니다.

${\displaystyle {\frac {n} {\text {core}}}:\sin \theta _{\max }=\cos \theta _{c}.}$

양쪽을 제곱하여

$({displaystyle {n^{2}}{n_{\text{core}^{2}}\sin ^{2}=\cos ^{2}\theta _{c}=1-\sin ^{2}=1-{\frac {n_{\textclad}^{2}}}{{core}})\sin ^{2} } } } {text} } } } } {core } }}$

문제를 해결하면 위의 공식을 찾을 수 있습니다.

${\displaystyle n\sin \theta _{\max }=sargrt {n_{\text{core}^2}-n_{\text{clad}^2}}}$

이것은 다른 광학 시스템의 수치 개구(NA)와 같은 형태를 가지고 있기 때문에, 모든 타입의 파이버의 NA를 정의하는 것이 일반화되어 있습니다.

${\displaystyle \mathrm {NA} = scarrt {n_{\text{core}^2}-n_{\text{clad}^2}}$

여기서_core n은 섬유 중심축을 따른 굴절률입니다.이 정의를 사용하면 NA와 파이버의 수용각 사이의 접속은 근사치일 뿐이라는 점에 주의해 주십시오.특히, 싱글 모드 파이버의 수용 각도는 상당히 다르며 굴절률만으로는 판단할 수 없지만, 제조사는 이 공식에 근거하여 싱글 모드 파이버의 "NA"를 인용하는 경우가 많습니다.

바운드 모드의 수, 모드 볼륨은 정규화된 주파수와 관련이 있으며, 따라서 NA와 관련이 있습니다.

멀티모드 파이버에서는 평형 수치 개구라는 용어가 사용되기도 한다.이는 평형 모드 분포가 확립된 섬유에서 발생하는 광선의 극한 출구 각도에 관한 수치 개구부를 말합니다.

「 」를 참조해 주세요.

• f-번호
• 숫자 개구부 실행
• 유도 광선, 광섬유 컨텍스트
• 수용 각도(태양광 집광 장치), 추가 컨텍스트

레퍼런스

• 이 문서에는 General Services Administration 문서의 퍼블릭 도메인 자료가 포함되어 있습니다(MIL-STD-188 지원).

외부 링크

• 「현미경 목적: Mortimer Abramowitz와 Michael W. Davidson의 "숫자 개구와 해상도", 분자식: 광학 현미경 프라이머(웹사이트), 2004년 4월 22일.
• 「현미경법의 기본 개념과 공식: 마이클 W. 데이비드슨, 니콘 현미경 U(웹사이트)의 수치 개구부.
• 레이저 물리 및 테크놀로지 백과사전(웹사이트).
• UCLA 뇌연구소 현미경 핵심설비(웹사이트), 2007.