보어-소머펠트 모형

1913년 수소 원자의 태양계 Bohr 모델의 Sommerfeld 확장은 스펙트럼 미세 구조를 설명하기 위해 타원 궤도의 추가를 보여준다.

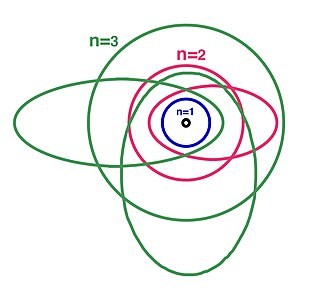
보어-소머펠트 모델(소머펠트 모델 또는 보어-소머펠트 이론으로도 알려져 있음)은 원자핵 주위의 전자의 타원 궤도를 허용하기 위해 보어 모델의 확장이었다.보어-소머펠트 이론은 덴마크 물리학자 닐스 보어와 독일 물리학자 아놀드 소머펠트의 이름을 따왔다.소머펠트는 만약 전자 궤도가 원형이 아닌 타원형이 될 수 있다면, 현재 양자 퇴행성이라고 알려진 것을 도입하면서 자기장의 존재를 제외하고 전자의 에너지는 같을 것이라고 주장했다.

Bohr-Sommerfeld 모델은 추가 방사형 양자화 조건인 Wilson-Sommerfeld 양자화 조건으로^[1]^[2] Bohr 모델의 양자화된 각운동량 조건을 보완했다.

\displaystyle \int _{0}^{T}p_{r},dq_{r}=nh,}

여기서_r p는 반경 위치인 좌표 q와 규범적으로 결합되는 반경 운동량이고 T는 전체 궤도 주기입니다.적분은 작용-각도 좌표의 작용입니다.대응 원리에 의해 제시된 이 조건은 양자수가 단열 불변이기 때문에 가능한 유일한 조건이다.

역사

1913년 닐스 보어는 나중에 정의된 대응 원리의 기초를 보여주었고 선 스펙트럼을 설명하는 수소 원자의 모델을 공식화하기 위해 그것을 사용했다.다음 몇 년 동안 Arnold Sommerfeld는 로렌츠와 아인슈타인에 의해 도입된 양자수의 단열 불변성 원리를 이용하여 양자 법칙을 임의의 적분 가능한 시스템으로 확장했다.소머펠트는 각운동량의 z-성분을 양자화함으로써 결정적인 기여를^[3] 했다.이 각운동량은 구 양자시대에는 "공간 양자화"라고 불렸다.리치퉁스완텔룽)이것은 전자의 궤도를 원이 아닌 타원형으로 만들 수 있게 했고, 양자 퇴화의 개념을 도입했다.이 이론은 전자 스핀 문제를 제외하고 제만 효과를 정확하게 설명했을 것이다.소머펠트의 모델은 보어의 모델보다 현대의 양자역학 그림에 훨씬 더 가까웠다.

1950년대에 조셉 켈러는 아인슈타인의 1917년 ^[4]해석을 이용하여 보어-소머펠트 양자화를 업데이트하였고, 현재는 아인슈타인-빌루인-켈러 방법이라고 알려져 있다.1971년 Martin Gutzwiller는 이 방법이 통합 가능한 시스템에만 적용된다는 것을 고려하였고 경로 ^[5]적분으로부터 혼돈 시스템을 수량화하는 반고전적인 방법을 도출하였다.

예측

소머펠트 모델은 축을 따라 측정된 원자의 자기 모멘트는 이산적인 값만을 취할 것이라고 예측했는데, 그 결과는 회전 불변성과 모순되는 것처럼 보이지만 스턴-게라크 실험에 의해 확인되었다.이것은 양자역학 발전의 중요한 단계였다.그것은 또한 원자 에너지 수준이 자기장에 의해 분할될 가능성을 묘사했다(제만 효과라고 불린다.발터 코셀은 첫 번째 껍질에 2개의 전자를 도입하고 두 ^[6]번째 껍질에 8개의 전자를 도입하는 원자의 보어-소머펠트 모델에 대해 보어 및 소머펠트와 함께 연구했다.

문제들

Bohr-Sommerfeld 모델은 근본적으로 일관성이 없었고 많은 역설로 이어졌다.자기 양자 수는 xy 평면에 대한 궤도 평면의 기울기를 측정했으며, 몇 개의 이산 값만 취할 수 있었습니다.이것은 원자가 제한 없이 좌표에 상대적인 방식으로 회전할 수 있다는 명백한 사실과 모순되었다.소머펠트 양자화는 다른 표준 좌표에서 수행될 수 있으며 때로는 다른 답을 제공합니다.방사선 보정의 통합은 어려웠는데, 이는 방사선이 빠져나갈 수 있는 경우 어려운 복합 방사선/원자 시스템에 대한 작용-각도 좌표를 찾아야 했기 때문이다.전체 이론은 통합 불가능한 운동으로 확장되지 않았고, 이는 많은 시스템이 원칙적으로도 처리될 수 없다는 것을 의미했다.결국 이 모델은 1925년 볼프강 파울리가 하이젠베르크의 매트릭스 역학을 이용해 처음 제시한 수소 원자의 현대 양자역학 처리로 대체됐다.현재 수소 원자의 그림은 에르빈 슈뢰딩거가 1926년에 개발한 파동 역학의 원자 궤도에 기초하고 있다.

그러나 이것이 보어-소머펠트 모델이 그 성공이 없었다고 말하는 것은 아니다.보어-소머펠트 모델에 기초한 계산은 보다 복잡한 원자 스펙트럼 효과를 정확하게 설명할 수 있었다.예를 들어, 1차 섭동까지, Bohr 모델과 양자 역학은 Stark 효과의 스펙트럼 선 분할에 대해 동일한 예측을 한다.그러나 고차 섭동에서는 Bohr 모델과 양자역학이 다르며, 높은 자기장 강도에서 Stark 효과를 측정함으로써 Bohr 모델에 대한 양자역학의 정확성을 확인할 수 있었다.이 차이 뒤에 있는 지배적인 이론은 전자의 에너지 상태에 따라 변하는 전자의 궤도 모양에 있다.

보어-소머펠트 양자화 조건은 현대 수학에서 질문으로 이어진다.일관된 반고전 양자화 조건은 위상공간에 특정 유형의 구조를 필요로 하며, 이는 양자화할 수 있는 심플렉틱 매니폴드의 유형에 위상적 한계를 둔다.특히 심플렉틱 형식은 사전 양자화라고 불리는 에르미트 선다발 연결의 곡률 형태여야 한다.

상대론적 궤도

동일한 에너지와 양자화된 각운동량을 갖는 타원궤도

Arnold Sommerfeld는 원자 에너지 ^[3]수준의 상대론적 해답을 도출했다.우리는 전위에서의 에너지에 대한 상대론적 방정식으로 이 유도를^[7] 시작할 것이다.

W={m_{\mathrm {0}c^{2}}\left\frac {1}{\frac {1-{\frac {v^{2}}}}}-1\right}-kcfrac {Ze^{2}}{r}

$u={\frac {1}{r}}$ 후 $u={\frac {1}{r}}$ $=$ 1 $u={\frac {1}{r}}$ { $display$ u = $snew frac$ {1} {r $}}$ 을 $u={\frac {1}{r}}$ (를) 받습니다.

{{displaystyle {\frac {1-{\frac {v^{2}}}{c^{2}}}}=1+{\frac {W}{m_{\mathrm {0}}c^{2}}+kfrac {Ze^{2}}{m_{\mathrm {0}}}^{{c}}}}}}}}{u}}}}}}}}}{u}}}}}}

$p_{\mathrm {r} }=m{\dot {r}}$ $p_{\mathrm {r} }=m{\dot {r}}$ r $p_{\mathrm {r} }=m{\dot {r}}$ $m$ $p_{\mathrm {r} }=m{\dot {r}}$ { $displaystyle$ p $_$ { \ $mathrm { r$ } $=$ $m dot$ $p_{\mathrm {\varphi } }=mr^{2}{\dot {\varphi }}$ { $r$ $p_{\mathrm {r} }=m{\dot {r}}$ } $p_{\mathrm {r} }=m{\dot {r}}$ 、 $p_{\mathrm {\varphi } }=mr^{2}{\dot {\varphi }}$ $p_{\mathrm {\varphi } }=mr^{2}{\dot {\varphi }}$ $m$ $p_{\mathrm {\varphi } }=mr^{2}{\dot {\varphi }}$ ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ $p_{\mathrm {\varphi } }=mr^{2}{\dot {\varphi }}$ ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ { \ $displaystyle$ p $_$ { \ $mathrm$ { \ $varphi }$ ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ $display$ style ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ style ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ style ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ ufficle }의 ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ $}}$ 운동방정식은 ${\frac {p_{\mathrm {r} }}{p_{\mathrm {\varphi } }}}=-{\frac {du}{d\varphi }}$ (비넷방정식 참조)

{d^{2}u}{d\varphi ^{2}=-\left(1-k^{2}{\frac {Z^{4}}{c^{2}p_{{2}}{{2}}{{{2}}}{{{{right}}}\frac {{{{{\mathm}}}}}}{\frac {\frac {\m}}}}}}}

해결책을 가지고

u=snarfrac {1}{r}}=K+A\cos \omega _{\mathrm {0}}\varphi

회전당 근점각의 각도 이동은 다음과 같이 주어진다.

\displaystyle \varphi _{\mathrm {s} = 2\pi \left\frac {1} {\mathrm {0}}-1\right}\pi ^{3}k^{2}{\frac {Z^{2}e^{4} {c^2}n} {\mathrmathrpi } {1} {{{1}

양자 조건과 함께

\displaystyle \point p_{\mathrm \varphi },d\varphi =2\pi p_{\mathrm \varphi }=n_{\mathrm \varphi } }h}

그리고.

\displaystyle \point p_{\mathrm {r}, dr=p_{\mathrm {varphi }}\point \leftfac\frac {1}{r}{dr}, d\varphi =n_{\mathrm {r} } }h}

우리는 에너지를 얻을 것이다

{m_{\mathrm {0} }c^{2} =\left(1+{\frac {alpha ^{2}Z^{2}} {\left(n_{\mathrm {rm {r}} + {\mathrm {vi} } ^2-{2}} ^2

$\alpha$ 서 $\alpha$ α {\ $displaystyle \alpha }$ 는 $\alpha$ 미세한 정수입니다.이 해는 (양자수에 대한 치환을 사용하여) 디랙 ^[8]방정식의 해와 동일합니다.그럼에도 불구하고 두 솔루션 모두 양 이동을 예측하지 못합니다.

「」를 참조해 주세요.

레퍼런스

^ A. Sommerfeld (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik (in German). 51 (17): 1–94. Bibcode:1916AnP...356....1S. doi:10.1002/andp.19163561702.
^ W. Wilson (1915). "The quantum theory of radiation and line spectra". Philosophical Magazine. 29 (174): 795–802. doi:10.1080/14786440608635362.
^ ^a ^b Sommerfeld, Arnold (1919). Atombau und Spektrallinien'. Braunschweig: Friedrich Vieweg und Sohn. ISBN 978-3-87144-484-5.
^ 알버트 아인슈타인의 논문집, 제6권, A. Engel, 트랜스, 프린스턴, 프린스턴, 뉴저지, (1997), 페이지 434
^ Stone, A.D. (August 2005). "Einstein's unknown insight and the problem of quantizing chaos" (PDF). Physics Today. 58 (8): 37–43. Bibcode:2005PhT....58h..37S. doi:10.1063/1.2062917.
^ 코셀-소머펠트 이론과 반지 원자, 존 L.Heilbron, Isis, Vol. 58, 4호(Winter, 1967), 450-485페이지(36페이지), The History of Science Society를 대표하여 시카고 대학 출판부
^ https://archive.org/details/atombauundspekt00sommgoog/page/n541 - Atombau und Spektralinien, 1921, 520페이지
^ Ya I Granovski (2004). "Sommerfeld formula and Dirac's theory" (PDF). Physics-Uspekhi. 47 (5): 523–524. Bibcode:2004PhyU...47..523G. doi:10.1070/PU2004v047n05ABEH001885. S2CID 250900220.

[1] A. Sommerfeld (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik (in German). 51 (17): 1–94. Bibcode:1916AnP...356....1S. doi:10.1002/andp.19163561702.

[2] W. Wilson (1915). "The quantum theory of radiation and line spectra". Philosophical Magazine. 29 (174): 795–802. doi:10.1080/14786440608635362.

[Sommerfeld-3] Sommerfeld, Arnold (1919). Atombau und Spektrallinien'. Braunschweig: Friedrich Vieweg und Sohn. ISBN 978-3-87144-484-5.

[4] 알버트 아인슈타인의 논문집, 제6권, A. Engel, 트랜스, 프린스턴, 프린스턴, 뉴저지, (1997), 페이지 434

[5] Stone, A.D. (August 2005). "Einstein's unknown insight and the problem of quantizing chaos" (PDF). Physics Today. 58 (8): 37–43. Bibcode:2005PhT....58h..37S. doi:10.1063/1.2062917.

[6] 코셀-소머펠트 이론과 반지 원자, 존 L.Heilbron, Isis, Vol. 58, 4호(Winter, 1967), 450-485페이지(36페이지), The History of Science Society를 대표하여 시카고 대학 출판부

[7] ttps://archive.org/details/atombauundspekt00sommgoog/page/n541 - Atombau und Spektralinien, 1921, 520페이지

[Granovski-8] Ya I Granovski (2004). "Sommerfeld formula and Dirac's theory" (PDF). Physics-Uspekhi. 47 (5): 523–524. Bibcode:2004PhyU...47..523G. doi:10.1070/PU2004v047n05ABEH001885. S2CID 250900220.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v t 양자역학
배경	서론 역사 타임라인 고전 역학 구 양자론 용어집
기초	타고난 규칙 브라켓 표기법 상보성 밀도 매트릭스 에너지 레벨 접지 상태 들뜬 상태 퇴화 수준 제로 포인트 에너지 얽힘 해밀턴식 방해다 데코히렌스 측정. 비국소성 양자 상태 중첩 터널링 산란 이론 양자역학에서의 대칭성 불확실성 파동 함수 접다 파동-입자 이중성
제제	제제 하이젠베르크 상호 작용 행렬 역학 슈뢰딩거 경로 적분 공식 위상 공간
방정식	디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석	해석 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션 폰 노이만 위그너
실험	벨 부등식 데이비슨-게르머 선택 지연 양자 지우개 더블 슬릿 프랑크-헤르츠 마하-젠더 간섭계 엘리추르-바이드만 포퍼 양자 지우개 스턴-게라크 Wheeler의 지연
과학	양자생물학 양자 화학 양자 카오스 양자 우주론 양자 미분학 양자역학 양자 기하학 양자 측정 문제 양자 확률 미적분 양자 시공간
테크놀로지	양자 알고리즘 양자 증폭기 양자 버스 양자 세포 오토마타 양자 유한 오토마타 양자 채널 양자 회로 양자 복잡도 이론 양자 컴퓨팅 타임라인 양자암호학 양자 전자 공학 양자 오차 보정 양자 이미징 양자 이미지 처리 양자 정보 양자 키 배포 양자 논리 양자 논리 게이트 양자 기계 양자 기계 학습 양자 메타물질 양자 도량형 양자 네트워크 양자 신경망 양자 광학 양자 프로그래밍 양자 감지 양자 시뮬레이터 양자 순간이동
내선번호	카시미르 효과 양자통계역학 양자장론 역사 양자 중력 상대론적 양자역학
관련된	슈뢰딩거의 고양이 대중문화에서. EPR 패러독스 양자 신비주의
카테고리 물리 포털 공통

Search

보어-소머펠트 모형

네임스페이스

더

목차

역사

예측

문제들

상대론적 궤도

「」를 참조해 주세요.

레퍼런스

Search

보어-소머펠트 모형

역사

예측

문제들

상대론적 궤도

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.