12 동등한 기질
12 equal temperament
12음 동일 기질은[a] 옥타브를 12부분으로 나누는 음악적 계통으로, 모두 로그 척도로 동일하게 담금질(평등한 간격)한 것으로, 12근 2(√122 ≈ 1.05946)와 같은 비율을 가지고 있다.그 결과 가장 작은 간격,½ 옥타브의 폭은 반음계 또는 반음계라고 한다.
12음 평등 기질은 오늘날 음악에서 가장 널리 퍼져 있는 시스템이다.그것은 18세기부터 클래식 음악을 시작으로 서양 음악의 지배적인 튜닝 시스템이었으며, 유럽은 그 이전 수천 년 동안 거의 독점적으로 그것의 근사치를 사용했다.[citation needed]그것은 다른 문화권에서도 사용되었다.
현대에 있어서 12-TET는 보통 440Hz의 표준 피치에 상대적으로 튜닝된다. 즉, 한 노트, A는 440헤르츠로 튜닝되고 다른 모든 노트는 주파수가 높거나 낮을 때 그것과 떨어져 있는 몇 개의 세미톤 배수로 정의된다.표준 피치가 항상 440Hz인 것은 아니다.그것은 지난 몇백년 동안 다양하고 일반적으로 증가했다.[1]
역사
12음 동일 기질을 정확히 계산한 공적이 빈번한 두 인물은 주자이유(추차이유라고도 로마자로 표기됨)이다.중국어: 1584년 朱載堉), 1585년 사이먼 스테빈.프리츠 A에 의하면Kuttner, 그"Chu-Tsaiyu 1584년에 평균율 mono-chords의 산술 계산에 매우 정밀한과 기발한 간단한 방법을 설명했다."며"시몬 스테빈 평균율의 움직임을 수학적 정의와 이에 해당하는 수치 값은 다소 덜 정확한 계산을 제공했다 알려진 것은 theory,[2]의 비평가. 1585세 이상."그 발전은 독립적으로 일어났다.[3]
케네스 로빈슨은 평등한 기질의 발명을 주자이유[4] 탓으로 돌리며 텍스트 인용문을 증거로 제시한다.[5]주자이유는 1584년부터 작성된 문자에서 "나는 새로운 시스템을 구축했다.나는 한 발을 다른 발을 추출할 숫자로 설정하고, 그것을 추출하는 비율을 사용한다.모두 합쳐서 12개 작전에서 피치파이퍼의 정확한 수치를 찾아내야 한다."[5]쿠트너는 이에 동의하지 않으며 자신의 주장이 "중대한 자격요건 없이는 옳다고 볼 수 없다"[2]고 말했다.쿠트너는 주 자이유나 사이먼 스테빈 어느 쪽도 동등한 기질을 달성하지 못했으며 둘 다 발명가로 취급되어서는 안 된다고 제안한다.[3]
중국
초기 역사
청동차임벨은 쩡의 이 후작(중국 청동기시대 기원전 5세기)의 무덤에서 발견된 많은 악기들 중 한 세트에 12개의 음의 세미 톤을 포함하여 C장조 키에 5개의 7음 옥타브 전체를 덮고 있다.[6]
평등한 기질에 대한 근사치는 370~447년부터 살았던 남과 북 왕조의 수학자인허청톈]에 의해 설명되었다.[7]그는 역사상 동등한 기질과 관련하여 가장 일찍 기록된 대략적인 숫자 시퀀스를 가지고 나왔다: 900 849802 758 715 677 638 601 536 536 509.5 479 450.[8]
주자이유
명궁의 왕자 주자이유(周 z ()는 원래 아버지가 상정했던 동등한 기질 사상을 바탕으로 30년간 연구에 몰두했다.그는 1580년에 출판된 그의 음악 달력 律暦通에서 그의 새로운 음조 이론을 설명했다.이에 뒤이어 1584년 그의 5000쪽 분량의 작품 《음악과 피치의 Complete Compendium of Music and Pitch》(Yuelü Quan shu 樂律書書)에서 12-TET에 대한 정밀한 수치 사양을 갖춘 평등한 기질의 새로운 이론에 대한 상세한 설명이 발표되었다.[9]조셉 니덤에 의해 연장된 계좌도 제공된다.[5]Zhu는 끈과 파이프의 길이를 연속적으로 ≈2 59 1.059463으로 나누고, 파이프 길이에 대해서는 22로 나누어 수학적으로 결과를 얻었는데,[10] 12 눈금(옥타브)이 지나면 길이가 2:2로 나누어졌다.
![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{12}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0e94dc870dfc2af0eb35a7b362eb3776054719)
마찬가지로 84 눈금(7 옥타브) 이후 길이는 128배수로 나누었다.
![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{84}=2^{7}=128}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc85da07cabc4f33cc3fc965e9ef6e74361e7c7)
주자이유는 수학적으로 평등한 기질 문제를 가장 먼저 풀었다는 평가를 받았다.[11]적어도 한 연구자는 중국의 예수회 신자인 마테오 리치가 그의 개인 일기에[11][12] 이 작품을 기록했고, 그 작품을 유럽으로 되돌려 보냈을지도 모른다고 제안했다.(주제의 표준 자료에는 그러한 이전이 언급되지 않는다.)[13]1620년, Zhu의 작품은 유럽의 수학자에[who?] 의해 언급되었다.[12]머레이 바부르는 "평등한 기질에 대한 정확한 수치를 인쇄한 것으로 처음 알려진 것은 차이위 왕자의 훌륭한 해결책이 수수께끼로 남아 있는 중국에서였다"[14]고 말했다.19세기 독일 물리학자 헤르만 폰 헬름홀츠는 '톤 센세이션(On the Sensions of Tone)'에서 중국 왕자(아래 참조)가 7음계의 음계를 도입했으며, 옥타브를 12개의 세미톤으로 나눈 것이 중국에서 발견됐다고 썼다.[15]
주자유는 3옥타브에 이르는 36개의 대나무 튜닝 파이프를 세트로 구성하여 그의 평등한 기질 이론을 설명하였고, 대나무의 종류, 페인트의 색, 길이와 내경 및 외경에 대한 상세한 명세서를 제시하였다.그는 또한 12줄 짜리 튜닝 악기를 만들었는데, 튜닝 피치 파이프 세트가 하단 캐비티 안에 숨겨져 있었다.1890년 브뤼셀의 음악원 박물관 큐레이터 빅토르 샤를 마힐론은 주자이유의 사양에 따라 피치 파이프 세트를 복제했다.그는 중국의 음조 이론은 서양보다 피치 파이프의 길이를 더 잘 알고 있었으며, 자이유 데이터에 따라 중복된 파이프 세트가 이 이론의 정확성을 증명했다고 말했다.
유럽
초기 역사
평등한 기질의 초기 논의 중 하나는 기원전 4세기 아리스토세누스의 저술에서 일어난다.[16]
빈첸초 갈릴레이(갈릴레오 갈릴레이의 아버지)는 12음 동일 기질을 가진 최초의 실용적인 옹호자 중 한 명이었다.그는 모든 '변환키'에 12음계의 색도 음계 각각에 댄스 스위트 세트를 작곡했으며, 또한 1584년 '프론모'에 24+1 리카르를 실었다.[17]그는 루트를 초조하게 만드는 데 18:17의 비율을 사용했다(순수 옥타브에 약간의 조정이 필요하긴 했지만).[18]
갈릴레이의 시골 사람이자 동료 루테니스트 지아코모 고르자니스(Giacomo Gorzanis)는 1567년까지 평등한 기질을 바탕으로 음악을 작곡했다.[19]고르자니스만이 모든 모드나 키를 탐구한 유일한 루테니스트는 아니었다.프란체스코 스피나치노는 1507년에 "Recercare de tutti li Toni"(모든 톤에서 Ricercar)를 썼다.[20]17세기에 루텐리스트 겸 작곡가인 John Wilson은 모든 주요/최소 키 24개를 포함하여 30개의 서론을 썼다.[21][22]헤니쿠스 그라마테우스는 1518년에 동등한 기질에 가까운 근사를 그렸다.평등한 기질에서의 최초의 튜닝 규칙은 조바니 마리아 란프랑코가 그의 "Scintille de musica"[23]에서 주었다.갈릴레이와 함께 극성을 부리는 자를리노는 처음에는 동등한 기질을 반대했지만 결국 1588년 그의 소플리멘티 음악가의 루테와 관련하여 그것에 양보했다.
사이먼 스테빈
서양에서 두 개의 열두 번째 뿌리와 관련된 동등한 기질에 대한 최초의 언급은 1884년 거의 3세기 후에 사후에 출판된 사이먼 스테빈의 원고 반 데 스피겔링 데르 싱콘(ca. 1605)에 나타났다.[24]그러나 그의 계산의 정확도가 불충분했기 때문에, 그가 얻은 화음 길이 번호들 중 많은 수가 정확한 값에서 1, 2단위 떨어져 있었다.[13]그 결과 사이먼 스테빈의 화음의 주파수 비율은 통일된 비율이 아니라 톤당 1개의 비율로 되어 있는데, 이는 진 조가 부정확하다고 주장한다.[25]
다음은 Van de Spiegheling der singconst에서 나온 Simon Stevin의 화음 길이였다.[26]
| 톤 | 사이먼 스테빈으로부터 코드 10000 | 비율 | 보정 화음 |
|---|---|---|---|
| 반음절 | 9438 | 1.0595465 | 9438.7 |
| 전체 음색 | 8909 | 1.0593781 | |
| 반음 반음 | 8404 | 1.0600904 | 8409 |
| 디톤을 칠하다 | 7936 | 1.0594758 | 7937 |
| 반반 | 7491 | 1.0594046 | 7491.5 |
| 삼중수소 | 7071 | 1.0593975 | 7071.1 |
| 삼중수소 반 | 6674 | 1.0594845 | 6674.2 |
| 사투리 | 6298 | 1.0597014 | 6299 |
| 사투리 반 | 5944 | 1.0595558 | 5946 |
| 오음조의 | 5611 | 1.0593477 | 5612.3 |
| 오음 반 | 5296 | 1.0594788 | 5297.2 |
| 풀톤 | 1.0592000 |
한 세대 후 프랑스의 수학자 마린 메르센은 장 보그랑, 이스마엘 부야루드, 장 갈레에 의해 얻은 몇 개의 동일한 강화 화음 길이를 제시했다.[27]
1630년 요한 파울하버가 100센트짜리 모노코드 테이블을 발행했는데, 여기에는 로그 테이블을 사용했기 때문에 여러 가지 오류가 포함되어 있었다.그는 어떻게 결과를 얻었는지 설명하지 않았다.[28]
바로크 시대
1450년 약 1800년까지, 뽑아 낸 계기 선수들(lutenists과 기타리스트)와 Brossard 류트 사본은 17세기 지난 분기 집계된 동등한 temperament,[29]18의 서곡 Bocquet 것으로 모든 키에 쓴 지난 서곡 포함한 시리즈가 포함되어 있으며, 혜택을 받을 자격이 서곡 제공하는 바 les톤, tous.해치다모든 키를 통해 모형으로 제작할 [30]수 있어안젤로 미첼레 바르톨로티는 모든 키에 일련의 파사카글리아(passacaglias)를 발표했는데, 그 내용은 무기력하게 변조된 구절을 연결했다.17세기 키보드 작곡가 중 지롤라모 프레스코발디는 평등한 기질을 주창했다.주세페 타르티니와 같은 몇몇 이론가들은 평등한 기질의 채택에 반대했다; 그들은 안드레아스 베르크마이스터가 사후 출간된 1707년 논문에서 평등한 기질을 강력히 주장했지만, 각 화음의 순수성을 떨어뜨리는 것은 음악의 미적 매력을 떨어뜨린다고 느꼈다.[31]
12음 대등한 기질이 여러 가지 이유로 잡혔다.기존의 키보드 설계에 편리한 것이었으며, 매 간격마다 중간 불순도의 부담, 특히 불완전한 조화가 허용되었다.이는 18세기에 프란체스코 게미니아니, 빌헬름 프리데만 바흐, 칼 필리프 에마누엘 바흐, 요한 고트프리드 뷔텔 등의 작곡가의 음악에서 극히 중요해진 무협적 변조를 통해 더 큰 표현을 할 수 있게 했다.[citation needed]12음 동일 기질에는 불완전한 3분의 1과 같은 단점이 있었지만, 유럽이 동일 기질로 전환함에 따라, 시스템을 수용하고 불협화음을 최소화하기 위해 작곡한 음악을 바꾸었다.[32]
평균율의 18세기 중반부터 공정 부분에 상당한 몇몇 현대적인 학술 간행물에:선택의 고전 주의 시대(18세기의 후반전)[표창 필요한]에 이미 그 기질과 그것은 초기 낭만 주의 시대(19세기의 10년),-LSB- 표창 동안 표준이 되었습니다 설명되어 있다. 는 swi 기관을 제외하고 해결을 써야 한다.19세기 2차 10년 만에 완성되면서 더 서서히 그것에 적응했다. (영국에서는, 몇몇 성당 오르가니스트들과 성가대 지휘자들이 그 날짜가 지난 후에도 그것에 대항하여 버텼다; 예를 들어, 새뮤얼 세바스찬 웨슬리는 내내 반대했다.1876년 사망하였다.)[citation needed]
옥타브를 먼저 3분의 3의 담금질 소령으로 나누는 17세기 사바티니 방법을 사용하면 정확한 평등한 기질이 가능하다.[33]이것은 또한 고전 시대 동안 몇몇 작가들에 의해 제안되었다.비트 전송률 없이 튜닝하지만 몇 가지 수표를 사용하여 사실상 현대적인 정확성을 달성한 것은 19세기 초 이미 이루어졌다.[34]1749년에 처음 제안된 박동수를 사용하는 것은 19세기 후반 헬름홀츠와 엘리스에 의해 확산된 이후 보편화되었다.[35]1917년 화이트가 발표한 2십진법 표로 궁극의 정밀도를 구할 수 있었다.[36]
대칭적인 톤과 다음성의 새로운 스타일, 12음 기법이나 연재주의로 쓰여진 것과 같은 무조 음악, 재즈(적어도 그 피아노 구성 요소)가 발달하고 번성하는 것은 평등한 기질의 환경에 있다.
세미톤의 역사근사 비교
| 연도 | 이름 | 비율[37] | 센트 |
|---|---|---|---|
| 400 | 허청톈 | 1.060070671 | 101.0 |
| 1580 | 빈첸초 갈릴레이 | 18:17 [1.058823529] | 99.0 |
| 1581 | 주자이유 | 1.059463094 | 100.0 |
| 1585 | 사이먼 스테빈 | 1.059546514 | 100.1 |
| 1630 | 마린 메르센 | 1.059322034 | 99.8 |
| 1630 | 요한 파울하버 | 1.059490385 | 100.0 |
수학적 특성
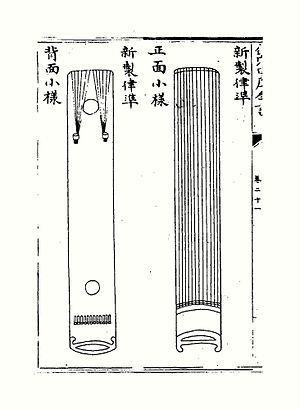
옥타브를 12등분하는 12음등성 기질에서, 세미톤의 폭, 즉 인접한 두 음의 간격의 빈도비(prequency ratio)는 2의 12번째 근이다.
![{\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)
이는 다음과 같다.
이 간격은 100센트로 나뉜다.
절대 주파수 계산
12-TET에서 노트의 주파수 P를n 찾으려면 다음 정의를 사용할 수 있다.
![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
이 공식에서 P는n 음치, 즉 주파수(보통 헤르츠 단위)를 가리키며, 당신은 찾으려 하고 있다.P는a 기준 피치의 주파수를 가리키며, n은 각각 원하는 피치와 기준 피치에 할당된 숫자를 가리킨다.이 두 숫자는 연속된 의미에 할당된 연속 정수의 목록에서 나온 것이다.예를 들어 A4(기준 피치)는 피아노 왼쪽 끝에서 49번째 키(440Hz로 튜닝됨), C(중간 C)와 F#4는4 각각 40번째와 46번째 키다.이 숫자들은 C와4 F#4의 주파수를 찾는 데 사용될 수 있다.
![{\displaystyle P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49)}\approx 261.626\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)
단지 간격
12-TET의 간격은 억양만으로 어떤 간격에 근접한 값이다.[38]
제한에 따라
12-TET는 3-리미트에서는 매우 정확하지만, 프라임 한계를 11로 증가시키면서 매회 약 6분의 1의 세미톤으로 점차 심해진다.그것의 열한번째와 열세번째의 고조파들은 극도로 부정확하다. 12-TET의 열일곱번째와 열아홉번째 고조파들은 그것의 세 번째 고조파만큼 거의 정확하지만, 이쯤 되자, 원초한계는 너무 높아져서 대부분의 사람들에게 자음을 낼 수 없게 되었다.[citation needed]
3시 30분
12-TET는 특히 옥타브를 비교적 적은 수의 톤으로 나누는 경우, 완벽한 5번째(3/2)와 그 반전인 4번째(4/3)에 대한 매우 좋은 근사치를 가지고 있다.구체적으로는, 딱 완벽한 5분의 1은 2센트에 약간 못 미치는데, 이것은 같은 성질의 근사치보다 더 날카로운 반음절의 50분의 1이다.주요 음색(9/8)은 단순히 옥타브를 뺀 두 개의 완벽한 5분의 1을, 그 반전인 피타고라스 단조 7단(16/9)은 단순히 두 개의 완전한 4분의 1을 합친 것이기 때문에, 그들은 대부분 전임자의 정확성을 유지한다; 오류는 두 배로 증가하지만, 사실 인간이 그것을 인식할 수 없을 정도로 작다.3의 힘을 가진 분수는 계속 사용할 수 있지만, 그 다음 두 가지는 27/16과 32/27이지만 분수의 조건이 커질수록 귀가 덜 즐겁다.[citation needed]
5시 15분
12-TET의 다섯 번째 고조파(5/4)의 근사치는 반투명의 1/6과 1/7 사이에 있다.12-TET는 스케일오프 4분의 1 미만의 구간이 여전히 조정에 따라 울리기 때문에 5/3 및 8/5와 같은 다른 5 한계 구간을 생성하는 데 사용할 수 있는 인튠 5번째 고조파를 가지고 있으며, 오차는 유사하다.서양음악은 4:5:6 산술 순서에서 사용하는 등 인튠 5번째 하모닉을 활용한다.[citation needed]
7시 15분
12-TET의 일곱 번째 고조파(7/4)의 근사치는 반투명의 약 1/3이다.오차가 세미톤의 4분의 1보다 크기 때문에 12-TET의 7제한 간격은 음이 맞지 않게 들리는 경향이 있다.트리톤 분율 7/5와 10/7에서 다섯 번째와 일곱 번째 고조파의 오차는 부분적으로 서로를 상쇄하여, 정당한 분율이 동일한 성질의 등가물의 4분의 1 반 내에 있게 되지만, 트리톤은 여전히 대부분의 사람들에게 불협화음으로 들린다.[citation needed]
11번과 13번가
11번째 고조파(11/8)는 약 550 센트로, 12-TET에서 가장 가까운 두 개의 동일한 성질의 간격 사이에 거의 정확하게 떨어지며, 따라서 어느 쪽에도 의해 근사치가 되지 않는다.사실 11/8은 12-TET에서 가능한 한 성질이 같은 근사치와는 거리가 멀다.13번째 고조파(13/8)는 거의 부정확하다.그러나 이는 11번째와 13번째 고조파의 오차가 서로를 상쇄하기 때문에 분율 13/11(및 그 반전, 22/13)이 정확히 12-TET(특히 3개의 반)로 근사하게 추정된다는 것을 의미한다.그러나, 대부분의 사람들은 열한번째와 열세번째 고조파에는 익숙하지 않기 때문에, 이 분수는 대부분의 사람들에게 자음으로 들리지 않을 것이다.마찬가지로 열한 번째 또는 열세 번째 고조파의 오차는 대부분 일곱 번째 고조파의 오차로 인해 취소될 수 있지만, 이전과 같은 이유로 대부분의 사람들은 결과 분수 자음을 찾지 못할 것이다.[citation needed]
17번과 19번.
17번째 고조파(17/16)는 12-TET의 한 세미톤보다 약 5센트밖에 더 날카롭지 않다.그것은 17/12를 산출하기 위해 12-TET의 세 번째 고조파 근사치, 즉 7/5 이후의 다음 Pell 근사치로서 동일한 성질의 트리톤(2의 제곱근)에서 약 3센트 떨어져 있을 뿐이며, 12-TET의 주요 7번째에서 불과 1센트 떨어져 있는 17/9와 결합할 수 있다.19번째 고조파는 12-TET의 반음 중 3개보다 약 2.5센트에 불과하므로 마찬가지로 3번째 고조파와 결합하여 19/12를 산출할 수 있는데, 이는 동일한 성질의 마이너 6번째보다 약 4/5센트가 높은 것이고, 세미톤보다 약 6/5센트가 더 높은 19/18을 산출할 수 있다.그러나 17과 19는 자음비용으로 다소 큰 편이고 대부분의 사람들이 17 한계와 19 한계 간격에 익숙하지 않기 때문에 17 한계와 19 한계 간격은 대부분의 목적에 유용하지 않기 때문에 12-TET의 어떤 조음에서도 한몫을 하는 것으로 판단되지 않을 가능성이 높다.[citation needed]
테이블
다음 표에서 다양한 정의 간격의 크기를 성질이 같은 상대와 비교하며, 비율은 센트(cent)이다.6센트 미만의 차이는 대부분의 사람들이 알아차릴 수 없고, 4분의 1보 이상 간격을 두고 있는데, 이 경우 25센트로 음이 맞지 않는다.[citation needed]
| 단계수 | C에서 위로 올라가는 노트 | 12-TET 단위의 정확한 값 | 12-TET 단위의 십진수 값 | 성질이 같은 오디오 | 센트 | 단순 억양 간격 이름 | 단지 억양 간격 분율 | 정곡을 찌른 오디오 | 억양만으로 센트 | 차이점 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | C | 20⁄12 = 1 | 1 |  놀이를 하다 (도움말/도움말) | 0 | 유니슨 | 1⁄1 = 1 | 놀이를 하다 (도움말/도움말) | 0 | 0 |
| 1 | C♯ 또는 D♭ | 21⁄12 = 12√2 | 1.05946… | 놀이를 하다 (도움말/도움말) | 100 | 9진법 제3음 | 28⁄27 = 1.03703… | 놀이를 하다 (도움말/도움말) | 62.96 | -37.04 |
| 그냥 색채 세미톤 | 25⁄24 = 1.04166… | 놀이 (도움말/도움말) | 70.67 | -29.33 | ||||||
| 미해결 세미톤 | 22⁄21 = 1.04761… | 놀이를 하다 (도움말/도움말) | 80.54 | -19.46 | ||||||
| 9진 색도 세미톤 | 21⁄20 = 1.04 | 놀이를 하다 (도움말/도움말) | 84.47 | -15.53 | ||||||
| 노반디칼 색도 세미톤 | 20⁄19 = 1.05263… | 놀이를 하다 (도움말/도움말) | 88.80 | -11.20 | ||||||
| 피타고라스 디아토닉 세미톤 | 256⁄243 = 1.05349… | 놀이를 하다 (도움말/도움말) | 90.22 | -9.78 | ||||||
| 더 큰 색채 세미톤 | 135⁄128 = 1.05468… | 놀이를 하다 (도움말/도움말) | 92.18 | -7.82 | ||||||
| 노벤데시멀 디아토닉 세미톤 | 19⁄18 = 1.05555… | 놀이를 하다 (도움말/도움말) | 93.60 | -6.40 | ||||||
| 9진 색도 반음계 | 18⁄17 = 1.05882… | 놀이를 하다 (도움말/도움말) | 98.95 | -1.05 | ||||||
| 열일음조 | 17⁄16 = 1.0625… | 놀이를 하다 (도움말/도움말) | 104.96 | +4.96 | ||||||
| just diatonic semoon | 16⁄15 = 1.06666… | 놀이를 하다 (도움말/도움말) | 111.73 | +11.73 | ||||||
| 피타고라스 색채 세미톤 | 2187⁄2048 = 1.06787… | 놀이를 하다 (도움말/도움말) | 113.69 | +13.69 | ||||||
| 십진음 이음 반음 | 15⁄14 = 1.07142… | 놀이를 하다 (도움말/도움말) | 119.44 | +19.44 | ||||||
| 작은 삼위일체 2/3-톤 | 14⁄13 = 1.07692… | 놀이를 하다 (도움말/도움말) | 128.30 | +28.30 | ||||||
| 주요 이음 세리톤 | 27⁄25 = 1.08 | 놀이를 하다 (도움말/도움말) | 133.24 | +33.24 | ||||||
| 2 | D | 22⁄12 = 6√2 | 1.12246… | 놀이를 하다 (도움말/도움말) | 200 | 피타고라스는 3위로 줄었다. | 65536⁄59049 = 1.10985… | 놀이를 하다 (도움말/도움말) | 180.45 | -19.55 |
| 마이너톤 | 10⁄9 = 1.11111… | 놀이를 하다 (도움말/도움말) | 182.40 | -17.60 | ||||||
| 주요음 | 9⁄8 = 1.125 | 놀이를 하다 (도움말/도움말) | 203.91 | +3.91 | ||||||
| 9진법 전음 | 8⁄7 = 1.14285… | 놀이를 하다 (도움말/도움말) | 231.17 | +31.17 | ||||||
| 3 | D♯ 또는 E♭ | 23⁄12 = 4√2 | 1.18920… | 놀이를 하다 (도움말/도움말) | 300 | 제9절단조 제3절 | 7⁄6 = 1.16666… | 놀이를 하다 (도움말/도움말) | 266.87 | -33.13 |
| 삼위일체 단조 3위 | 13⁄11 = 1.18181… | 놀이를 하다 (도움말/도움말) | 289.21 | -10.79 | ||||||
| 피타고라스 단조 3위 | 32⁄27 = 1.18518… | 놀이를 하다 (도움말/도움말) | 294.13 | -5.87 | ||||||
| 열아홉의 조화 | 19⁄16 = 1.1875 | 놀이를 하다 (도움말/도움말) | 297.51 | -2.49 | ||||||
| 단조 3위 | 6⁄5 = 1.2 | 놀이를 하다 (도움말/도움말) | 315.64 | +15.64 | ||||||
| 피타고라스 증강 2위 | 19683⁄16384 = 1.20135… | 놀이를 하다 (도움말/도움말) | 317.60 | +17.60 | ||||||
| 4 | E | 24⁄12 = 3√2 | 1.25992… | 놀이를 하다 (도움말/도움말) | 400 | 피타고라스는 4위로 줄었다. | 8192⁄6561 = 1.24859… | 놀이를 하다 (도움말/도움말) | 384.36 | -15.64 |
| 그냥 3중창. | 5⁄4 = 1.25 | 놀이를 하다 (도움말/도움말) | 386.31 | -13.69 | ||||||
| 피타고라스 제3장조 | 81⁄64 = 1.265625 | 놀이를 하다 (도움말/도움말) | 407.82 | +7.82 | ||||||
| 불문율장3길 | 14⁄11 = 1.27272… | 놀이 (도움말/도움말) | 417.51 | +17.51 | ||||||
| 제9장조 제3장조 | 9⁄7 = 1.28571… | 놀이를 하다 (도움말/도움말) | 435.08 | +35.08 | ||||||
| 5 | F | 25⁄12 = 12√32 | 1.33484… | 놀이를 하다 (도움말/도움말) | 500 | 딱 완벽한 4번째 | 4⁄3 = 1.33333… | 놀이를 하다 (도움말/도움말) | 498.04 | -1.96 |
| 피타고라스 증강 3위 | 177147⁄131072 = 1.35152… | 놀이를 하다 (도움말/도움말) | 521.51 | +21.51 | ||||||
| 6 | F♯ 또는 G♭ | 26⁄12 = √2 | 1.41421… | 놀이를 하다 (도움말/도움말) | 600 | 클래식 증강 4차 | 25⁄18 = 1.38888… | 놀이를 하다 (도움말/도움말) | 568.72 | -31.28 |
| 후이겐스 트리톤 | 7⁄5 = 1.4 | 놀이를 하다 (도움말/도움말) | 582.51 | -17.49 | ||||||
| 피타고라스는 5위로 줄었다. | 1024⁄729 = 1.40466… | 놀이를 하다 (도움말/도움말) | 588.27 | -11.73 | ||||||
| 방금 증강된 4번째 | 45⁄32 = 1.40625 | 놀이 (도움말/도움말) | 590.22 | -9.78 | ||||||
| 5번째 줄였다. | 64⁄45 = 1.42222… | 놀이를 하다 (도움말/도움말) | 609.78 | +9.78 | ||||||
| 피타고라스 증강 4위 | 729⁄512 = 1.42382… | 놀이를 하다 (도움말/도움말) | 611.73 | +11.73 | ||||||
| 오일러삼중수소 | 10⁄7 = 1.42857… | 놀이 (도움말/도움말) | 617.49 | +17.49 | ||||||
| 클래식 5위 감소 | 36⁄25 = 1.44 | 놀이를 하다 (도움말/도움말) | 631.28 | +31.28 | ||||||
| 7 | G | 27⁄12 = 12√128 | 1.49830… | 놀이를 하다 (도움말/도움말) | 700 | 피타고라스는 6번째로 줄어들었다. | 262144⁄177147 = 1.47981… | 놀이를 하다 (도움말/도움말) | 678.49 | -21.51 |
| 딱 5위. | 3⁄2 = 1.5 | 놀이를 하다 (도움말/도움말) | 701.96 | +1.96 | ||||||
| 8 | G♯ 또는 A♭ | 28⁄12 = 3√4 | 1.58740… | 놀이를 하다 (도움말/도움말) | 800 | 제9절단조 제6절 | 14⁄9 = 1.55555… | 놀이를 하다 (도움말/도움말) | 764.92 | -35.08 |
| 불초소6길 | 11⁄7 = 1.57142… | 놀이를 하다 (도움말/도움말) | 782.49 | -17.51 | ||||||
| 피타고라스 단조 6위 | 128⁄81 = 1.58024… | 놀이를 하다 (도움말/도움말) | 792.18 | -7.82 | ||||||
| 단조로운 6번째 | 8⁄5 = 1.6 | 놀이를 하다 (도움말/도움말) | 813.69 | +13.69 | ||||||
| 피타고라스 증강 5위 | 6561⁄4096 = 1.60180… | 놀이를 하다 (도움말/도움말) | 815.64 | +15.64 | ||||||
| 9 | A | 29⁄12 = 4√8 | 1.68179… | 놀이를 하다 (도움말/도움말) | 900 | 피타고라스는 7위로 줄었다. | 32768⁄19683 = 1.66478… | 놀이를 하다 (도움말/도움말) | 882.40 | -17.60 |
| 6단조. | 5⁄3 = 1.66666… | 놀이를 하다 (도움말/도움말) | 884.36 | -15.64 | ||||||
| 제19차 하화음 | 32⁄19 = 1.68421… | 놀이를 하다 (도움말/도움말) | 902.49 | +2.49 | ||||||
| 피타고라스 제6장조 | 27⁄16 = 1.6875 | 놀이를 하다 (도움말/도움말) | 905.87 | +5.87 | ||||||
| 제6장조 | 12⁄7 = 1.71428… | 놀이 (도움말/도움말) | 933.13 | +33.13 | ||||||
| 10 | A♯ 또는 B♭ | 210⁄12 = 6√32 | 1.78179… | 놀이를 하다 (도움말/도움말) | 1000 | 하모니 7단 | 7⁄4 = 1.75 | 놀이를 하다 (도움말/도움말) | 968.83 | -31.17 |
| 피타고라스 단조 7단조 | 16⁄9 = 1.77777… | 놀이를 하다 (도움말/도움말) | 996.09 | -3.91 | ||||||
| 큰소조7길 | 9⁄5 = 1.8 | 놀이를 하다 (도움말/도움말) | 1017.60 | +17.60 | ||||||
| 피타고라스 증강 6위 | 59049⁄32768 = 1.80203… | 놀이를 하다 (도움말/도움말) | 1019.55 | +19.55 | ||||||
| 11 | B | 211⁄12 = 12√2048 | 1.88774… | 놀이를 하다 (도움말/도움말) | 1100 | 삼위중립 7번째 | 13⁄7 = 1.85714… | 놀이를 하다 (도움말/도움말) | 1071.70 | -28.30 |
| 피타고라스는 옥타브를 줄였다. | 4096⁄2187 = 1.87288… | 놀이를 하다 (도움말/도움말) | 1086.31 | -13.69 | ||||||
| 7단조. | 15⁄8 = 1.875 | 놀이를 하다 (도움말/도움말) | 1088.27 | -11.73 | ||||||
| 17번째 부화음 | 32⁄17 = 1.88235… | 놀이를 하다 (도움말/도움말) | 1095.04 | -4.96 | ||||||
| 피타고라스 제7장조 | 243⁄128 = 1.89843… | 놀이를 하다 (도움말/도움말) | 1109.78 | +9.78 | ||||||
| 제7장조 | 27⁄14 = 1.92857… | 놀이를 하다 (도움말/도움말) | 1137.04 | +37.04 | ||||||
| 12 | C | 212⁄12 = 2 | 2 | 놀이를 하다 (도움말/도움말) | 1200 | 옥타브 | 2⁄1 = 2 | 놀이를 하다 (도움말/도움말) | 1200.00 | 0 |
콤마스
12-TET 템퍼는 여러 개의 쉼표를 나타내며, 이는 서로 다른 분수를 동일한 성질의 간격으로 매핑하기 때문에 1⁄1 x 12-TET로 처리되는 ½에 가까운 분수가 여러 개 있다는 것을 의미한다.예를 들어 729⁄512 (36⁄29)와 1024⁄729 (⁄310)는6 각각 트리톤에 매핑되어 있으므로, 같은 간격으로 처리되므로, 그들의 몫인 531441 ⁄524288 (312⁄219)은 일치로/처리된다.이것은 피타고라스의 쉼표인데, 12-TET의 유일한 쉼표다.그러나, 1차 한계를 증가시키고 더 많은 간격을 포함함에 따라 쉼표 수가 증가한다. 12-TET의 가장 중요한 5제한 쉼표는 810⁄80 (34⁄24×51)이며, 이는 싱토닉 쉼표로 알려져 있으며 피타고라스 3분의 3과 6분의 1과 그 정당한 상대 사이의 요인이다. 12-TET의 다른 5제한 쉼표는 다음과 같다.
- 스시마: 32805⁄32768=38×51⁄215=(531441⁄524288)×(181⁄80)−1
- 디아시스마: 2048⁄2025=211⁄34×52=(531441⁄524288)×(−181⁄80)2
- 소다이스: 128⁄125=27⁄53=(531441⁄524288)×(−181⁄80)3
- 더 큰 다이시스: 648⁄625=234×3⁄54=(531441⁄524288)×(−181⁄80)4
12-TET 템퍼에서 나오는 7-제한 쉼표 중 하나는 225⁄224 또는2 3×52⁄25×7과1 같은 9분의 1 클리마이다. 12-TET의 다른 7-제한 쉼표에는 다음이 포함된다.
- 9진수 세미옴마:−1 126⁄125=21×32×71⁄53=(81⁄80)×(1225⁄224)
- Archytas의 쉼표: 64⁄632=26⁄3×71= (531441⁄524288)×−1 (818)×2 (810)× (225⁄224)1
- 9분의 1음절: 36⁄35=22×32×51×71=(531441⁄524288)×(−181⁄80)×(3225⁄224)1
- 주빌리스마: 50½49=21×52⁄72=(531441⁄524288)×(−181⁄80)×(2225⁄224)2
유사 튜닝 시스템
역사적으로, 다중 튜닝 시스템은 12-TEDO의 약간의 변화로 볼 수 있으며, 옥타브 당 12노트가 있지만, 음의 간격이 상당히 균등하지 않도록 간격 크기 간에 약간의 변화를 가지고 있다.이것의 한 예로 성질이 같은 700센트의 5분의 1이 정의로운 701.955센트의 5분의 1의 5분의 1로 대체되는 3한계의 척도를 들 수 있다.두 구간이 옥타브의 1½600분의 2센트 미만으로 차이가 나기 때문에 두 척도는 매우 비슷하다.전에 그는 Chengtian 유럽에서 12-TEDO.[39]마찬가지로 고대 그리스인들에 의해 개발된 피타 고라스 튜닝은 지배적인 시스템의 시퀀스를 만들어 낼 때까지 르네상스 시대 동안, 유럽인들은 81⁄64[40] 같은 불협화음의 간격mo. 만들어질 수 있다는 것을 깨달았다 사실, 중국어 적어도 한세기 3-limit 단지 억양을 개발했다이 전무하다는 단점을5⁄4와 같은 단순한 비율로 그것들을 조절함으로써 유럽은 일련의 평균적인 기질을 개발하게 되는데, 이 기질은 간격 크기를 약간 수정했지만 여전히 대략 12-TEDO로 볼 수 있다.오류를 하나의 극초음 퍼펙트 5에 집중시켜 매우 불협화음을 내는 하나의 성질의 평균적인 경향 때문에, 안드레아스 베르크마이스터, 요한 필립 크렌베르거, 프란체스코 안토니오 발로티, 토마스 영과 같은 유럽의 음악 이론가들은 디아이를 줄이기 위해 콤마를 분할하는 것을 목표로 다양한 좋은 성질을 만들어냈다.가장 나쁜 영향을 받는 간격의 음소음베르크메이스터와 키른베르거는 각각 자신의 첫 기질에 불만족스러웠으며 따라서 여러 기질을 만들어냈는데, 후자 기질은 이전 기질보다 더 밀접하게 동등한 기질에 가깝다.마찬가지로, 유럽은 전체적으로 평균적이고 양호한 기질에서 오늘날에도 여전히 사용하고 있는 시스템인 12-TEDO로 점차 전환되었다.
하위 집합
직렬주의와 같은 어떤 종류의 음악은 12-TEDO의 12 음을 모두 사용하지만, 대부분의 음악은 음계라고 알려진 12-TEDO의 특정 부분집합에서 나오는 음표만을 사용한다.많은 다른 종류의 척도가 존재한다.
12-TEDO에서 가장 인기 있는 축척 유형은 하나를 의미한다.Mednone은 모든 음이 5초 원 위에 연속되는 척도를 가리킨다.크기가 다른 하나의 평균 음계가 존재하며, 사용된 평균 음계에는 5음표 평균 하나, 7음 평균 하나, 9음 평균이 포함된다.Simpedone은 서양 악기 디자인에 존재한다.예를 들어, 피아노의 키와 이전 피아노의 키들은 하나의 음계를 의미하고, 검은색 키는 하나의 음계를 의미하도록 구성된다.또 다른 예는 기타와 기타 현악기가 적어도 5개의 현을 가진 현악기를 적어도 5개의 현악기가 하나의 음계를 의미하도록 일반적으로 튜닝하는 것이다.
12-TEDO에서 사용되는 다른 척도에는 오름차순 멜로디 단음계, 고조파 단음계, 고조파 장음계, 감소된 척도, 척도 등이 있다.
참고 항목
참조
각주
인용구
- ^ 폰 헬름홀츠 & 엘리스 1885, 페이지 493–511.
- ^ a b 쿠트너 1975, 페이지 163.
- ^ a b 커트너 1975, 페이지 200.
- ^ 로빈슨 1980, 페이지 7: 추-차이유는 세계 어느 곳에서나 "평등한 기질"의 수학의 첫 공식화자.
- ^ a b c 니덤, 링 & 로빈슨 1962페이지
- ^ 광치창, 핑팡 쉬 & 롄청 루 2005 페이지 140-.
- ^ Goodman, Howard L.; Lien, Y. Edmund (April 2009). "A Third Century AD Chinese System of Di-Flute Temperament: Matching Ancient Pitch-Standards and Confronting Modal Practice". The Galpin Society Journal. Galpin Society. 62: 7. JSTOR 20753625.
- ^ 바버 2004, 페이지 55-56.
- ^ 하트 1998.
- ^ 니덤 & 로난 1978, 페이지 385.
- ^ a b 조 2010.
- ^ a b 롄하르트 1997.
- ^ a b Christensen 2002 페이지 205.
- ^ 바버 2004, 페이지 7.
- ^ 폰 헬름홀츠 & 엘리스 1885 페이지 258.
- ^ 참 2018년, 61-74페이지.
- ^ 갈릴리 1584, 페이지 80-89.
- ^ 바버 2004, 페이지 8.
- ^ 드 고르자니스 1981.
- ^ "Spinacino 1507a: Thematic Index". Appalachian State University. Archived from the original on 2011-07-25. Retrieved 2012-06-14.
- ^ 윌슨 1997.
- ^ 요르겐스 1986.
- ^ "Scintille de musica", (브레시아, 1533), 페이지 132
- ^ 코헨 1987, 페이지 471–488.
- ^ 조 2003, 223페이지.
- ^ 조 2003 페이지 222.
- ^ 2002년 크리스텐슨 페이지 207.
- ^ 2002년 크리스텐슨 페이지 78.
- ^ 마크 린들리 ISBN 978-0-521-2883-5
- ^ Vm7 6214
- ^ 안드레아스 베르크메이스터:뮤지컬리스 패러독스-디스코스, 1707
- ^ "12edo - Xenharmonic Wiki". en.xen.wiki. Retrieved 4 April 2020.
It is probably not an accident that as tuning in European music became increasingly close to 12et, the style of the music changed so that the defects of 12et appeared less evident, though it should be borne in mind that in actual performance these are often reduced by the tuning adaptations of the performers.
- ^ 디 베롤리 2009, 페이지 140, 142 및 256.
- ^ 무디 2003.
- ^ 폰 헬름홀츠 & 엘리스 1885 페이지 548.
- ^ 화이트, 윌리엄 브레이드피아노 튜닝과 연합 예술. 1917년, 제5회 확대판, 튜너 서플라이어 컴퍼니, 1946년 보스턴, 페이지 68.
- ^ 바버 2004, 페이지 55-78.
- ^ 1979년 파트치 134페이지
- ^ 니덤, 링 & 로빈슨 1962 페이지 170–171.
- ^ 벤워드 & 세이커 2003, 페이지 56.
원천
- Barbour, James Murray (2004). Tuning and Temperament: A Historical Survey. Courier Corporation. ISBN 978-0-486-43406-3.
- Benward, Bruce; Saker, Marilyn (2003). Music in Theory and Practice. Vol. 1. McGraw-Hill. ISBN 978-0-07-294261-3.
- Cho, Gene J. (2003). The Discovery of Musical Equal Temperament in China and Europe in the Sixteenth Century. E. Mellen Press. ISBN 978-0-7734-6941-9.
- Cho, Gene J. (2010). "The Significance of the Discovery of the Musical Equal Temperament in the Cultural History". Journal of Xinghai Conservatory of Music.
- Christensen, Thomas (2002). The Cambridge History of Western Music Theory. Cambridge University Press. ISBN 978-0-521-62371-1.
- Cohen, H. Floris (1987). "Simon Stevin's equal division of the octave". Annals of Science. Informa UK Limited. 44 (5): 471–488. doi:10.1080/00033798700200311. ISSN 0003-3790.
- de Gorzanis, G. (1981). Intabolatura di liuto: I-III. Intabolatura di liuto: I-III (in Italian). Minkoff. ISBN 978-2-8266-0721-2.
- Di Veroli, Claudio (2009). Unequal Temperaments: Theory, History and Practice (2nd ed.). Bray, Ireland: Bray Baroque.
- Galilei, Vincenzo (1584). Il Fronimo. Venice: Girolamo Scotto.
- Hart, Roger (1998), Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China, Departments of History and Asian Studies, University of Texas, Austin, archived from the original on 2012-03-05, retrieved 2012-03-20
- Jorgens, Elise Bickford (1986). English Song, 1600-1675: Facsimiles of Twenty-six Manuscripts and an Edition of the Texts. Garland.
- Kuttner, Fritz A. (May 1975). "Prince Chu Tsai-Yü's Life and Work: A Re-Evaluation of His Contribution to Equal Temperament Theory" (PDF). Ethnomusicology. 19 (2): 163–206. doi:10.2307/850355. JSTOR 850355.
- Kwang-chih Chang; Pingfang Xu; Liancheng Lu (2005). "The eastern Zhou and the growth of regionalism". The Formation of Chinese Civilization: An Archaeological Perspective. Xu Pingfang, Shao Wangping, Zhang Zhongpei, Wang Renxiang. Yale University Press. ISBN 978-0-300-09382-7.
- Lienhard, John H. (1997). "Equal Temperament". The Engines of Our Ingenuity. University of Houston. Retrieved 2014-10-05.
- Moody, Richard (February 2003). "Early Equal Temperament, An Aural Perspective: Claude Montal 1836". Piano Technicians Journal. Kansas City.
- Needham, Joseph; Ling, Wang; Robinson, Kenneth G. (1962). Science and Civilisation in China. Volume 4 - Part 1. Cambridge University Press. ISBN 978-0-521-05802-5.
- Needham, Joseph; Ronan, Colin A. (1978). The Shorter Science and Civilisation in China. Volume 4 - Part 1. Cambridge University Press.
- Partch, Harry (1979). Genesis of a Music (2nd ed.). Da Capo Press. ISBN 0-306-80106-X.
- Robinson, Kenneth (1980). A Critical Study of Chu Tsai-yü's Contribution to the Theory of Equal Temperament in Chinese Music. Volume 9 of Sinologica Coloniensia. Wiesbaden: Steiner. ISBN 978-3-515-02732-8.
- Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale (2nd ed.). London: Springer-Verlag. ISBN 1-85233-797-4.
- True, Timothy (2018). "The Battle Between Impeccable Intonation and Maximized Modulation". Musical Offerings. 9 (2): 61–74. doi:10.15385/jmo.2018.9.2.2.
- von Helmholtz, Hermann; Ellis, Alexander J. (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music (2nd ed.). London: Longmans, Green.
- Wilson, John (1997). "Thirty preludes in all (24) keys for lute [DP 49]". The Diapason Press. Retrieved 27 October 2020.
추가 읽기
- 더핀, 로스 W.평등한 기질이 어떻게 조화를 망쳤는가(그리고 왜 신경을 써야 하는가).W.W. Norton & Company, 2007.
- 조겐슨, 오웬튜닝.1991년 미시간 주립대학 출판부.ISBN 0-87013-290-3
- 흐라모프, 미하일로"5한계의 근사치, 억양만 있으면 된다.옥타브 등분할 음수계에서의 컴퓨터 MIDI 모델링", 국제회의 SIGMAP-2008[permanent dead link], 2008년 7월 26–29, Porto, 181–184, ISBN 978-989-8111-60-9
- Surjodingrat, W, Sudarjana, P.J., Susanto, A. (1972) Jogjakarta와 Surakarta, Gadjah Mada University Press, Jogjakarta 1972.https://web.archive.org/web/20050127000731/http:///web.telia.com/~u57011259/pelog_main.htm에서 인용.2006년 5월 19일 회수.
- 스튜어트, P. J. (2006) "갤럭시에서 갤럭시까지:구들의 음악" [1]
- 톤의 감각은 음향과 헤르만 폰 헬름홀츠에 의한 소리의 인식에 관한 기초적인 저작이다.특히 부록 XX: 번역자에 의한 추가사항, 페이지 430-556, (pdf 페이지 451-577)]
외부 링크
- EDO의 Xenharmonic wiki vs.이퀄리티 템즈
- Huygens-Fokker Foundation Center for Microtonal Music
- 올란디니:음악 음향학
- 체임버스의 사이클로페디아(1753) 부록의 "온도"
- 바르비에리, 파트리치오.Enharmonic 악기와 음악, 1470–1900 Wayback Machine에 2009-02-15 보관.(2008) 라티나, 일레반테 리브레리아 편집리스
- 프랙탈 마이크로토널 뮤직, 짐 쿠쿨라.
- 현존하는 모든 18세기의 인용구는 J.S. 바흐와 기질에 관한 것이다.
- 도미니크 에커슬리: "로세타 재방문: 바흐의 아주 평범한 기질"
- Well Meatments, Werckmeister 정의에 기초한 웰 템스
- Peter Buch가 선호하는 척도 기준
