회절

에 관한 일련의 기사의 일부
양자역학
${\displaystyle i\hbar {\frac t} \psi (t) \rangle = {H} \psi (t) \rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전 역학 구 양자론 브라켓 표기법 해밀턴식 방해다
기초 상보성 데코히렌스 얽힘 에너지 레벨 측정. 비국소성 양자수 주 중첩 대칭 터널링 불확실성 파동 함수 접다
실험 벨 부등식 데이비슨-게르머 더블 슬릿 엘리추르-바이드만 프랑크-헤르츠 레깃-가르그 부등식 마흐-젠더 포퍼 양자 지우개 선택 지연 슈뢰딩거의 고양이 스턴-게라크 휠러의 지연 선택
제제 개요 하이젠베르크 상호 작용 매트릭스 위상 공간 슈뢰딩거 Sum-over-History(경로 적분)
방정식 디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석 개요 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션
상세 토픽 상대론적 양자역학 양자장론 양자정보과학 양자 컴퓨팅 양자 카오스 밀도 매트릭스 산란 이론 양자통계역학 양자 기계 학습
과학자 아하로노프 벨 베테 블래킷 블로치 쾅 보어 태어난 보스 드 브로글리 콤프턴 디락 데이비슨 데비 에렌페스트 아인슈타인 에버렛 폭 페르미 파인만 글라우버 거츠빌러 하이젠베르크 힐베르트 조던 크래머스 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 온네스 플랑크 라비 라만 리드버그 슈뢰딩거 시몬스 솜메르펠트 폰 노이만 와일 빈 위그너 지만 자이링거
v t

회절은 파도가 장애물이나 개구부와 마주쳤을 때 발생하는 다양한 현상을 말한다.장애물의 모서리 주변 또는 장애물의 기하학적 그림자 영역으로의 개구부를 통해 파도의 간섭 또는 굴곡으로 정의됩니다.회절 물체 또는 개구부는 효과적으로 전파파의 2차 소스가 됩니다.이탈리아 과학자 프란체스코 마리아 그리말디는 회절이라는 단어를 만들었고 1660년에 ^[1][2]현상에 대한 정확한 관찰을 기록한 최초의 과학자였습니다.

고전 물리학에서 회절 현상은 전파 파면의 각 점을 개별 구면 웨이브릿의 ^[3]집합으로 처리하는 호이겐스-프레스널 원리에 의해 설명된다.삽입된 이미지에서 보듯이 간섭성 소스(레이저 등)로부터의 파장이 파장과 동등한 슬릿/어퍼처와 접촉할 때 특징적인 벤딩 패턴이 가장 두드러집니다.이는 다른 길이의 경로를 통해 레지스터 표면에 이동하는 파면(또는 동등한 각 웨이브릿)의 서로 다른 포인트가 추가 또는 간섭되기 때문입니다.간격이 촘촘한 개구부(예: 회절 격자)가 여러 개 있는 경우 강도가 변화하는 복잡한 패턴이 발생할 수 있습니다.

이러한 효과는 또한 광파가 굴절률이 다른 매체를 통과할 때 또는 음파가 다양한 음향 임피던스를 가진 매체를 통과할 때 발생합니다. 중력파,^{[citation needed]} 물파, 그리고 X선이나 전파와 같은 다른 전자파를 포함한 모든 파장이 회절됩니다.게다가, 양자역학은 또한 물질이 파동과 같은 특성을 가지고 있고, 따라서 회절(아원자에서 ^[4]분자 수준으로 측정할 수 있음)을 겪는다는 것을 증명한다.

역사

빛의 회절의 효과는 처음에 주의 깊게 관찰되었고, 프란체스코 마리아 그리말디가 또한 라틴어 회절이라는 용어를 만들어 냈는데, 그는 빛이 다른 방향으로 분해되는 것을 언급하며, '조각으로 쪼개지다'라는 용어를 만들었다.그리말디의 관찰 결과는 1665년에 ^[5][6][7]사후에 출판되었다.아이작 뉴턴은 이러한 효과들을 연구했고 빛의 유연성에 기인했다.제임스 그레고리 (1638–1675)는 효과적으로 발견된 최초의 회절 격자였던 새의 깃털에 의해 ^[8]야기된 회절 패턴을 관찰했습니다.Thomas Young은 1803년에 두 개의 좁은 ^[9]틈으로부터의 간섭을 증명하는 유명한 실험을 수행했다.그는 두 개의 다른 구멍에서 나오는 파장의 간섭에 의한 결과를 설명하면서 빛이 파장으로 전파되어야 한다고 추론했다.오거스틴-진 프레넬은 회절의 보다 결정적인 연구와 계산을 수행했고^[10], 1816년과 ^[11]1818년에 공개되었고, 이에 따라 크리스티안^[12] 호이겐스가 뉴턴의 입자 이론에 맞서 영에 의해 재활성화된 빛의 파동 이론을 크게 지지했다.

메커니즘

고전 물리학에서 회절은 파동이 전파되는 방식 때문에 발생한다; 이것은 Huygens-Fresnel 원리와 파동의 중첩 원리로 설명된다.파형의 전파는 파면상의 송신 매체의 모든 입자를 2차 구형파의 점원으로 간주함으로써 시각화할 수 있다.이후의 모든 지점에서의 파동 변위는 이러한 2차 파동의 합계입니다.파동이 합산될 때 파동의 합계는 개별 파동의 진폭뿐만 아니라 상대적인 위상에 의해 결정되므로 파동의 합산 진폭이 0과 개별 진폭의 합 사이의 값을 가질 수 있습니다.따라서, 회절 패턴은 보통 일련의 최대값과 최소값을 가지고 있다.

슬릿(또는 슬릿)을 통한 빛의 전파에 대한 현대의 양자역학적 이해에서 모든 광자는 파동함수라고 알려진 것을 가지고 있다.파동 기능은 슬릿 지오메트리, 스크린 거리 및 광자가 생성되었을 때의 초기 조건과 같은 물리적 환경에 의해 결정됩니다.중요한 실험에서는 (저강도 이중 슬릿 실험이 G.I에 의해 처음 수행되었다.)1909년 Taylor는 광자의 파동 함수의 존재를 증명하였다.)양자적 접근에서 회절 패턴은 확률 분포에 의해 생성되며, 명암 대역의 관찰은 이들 입자가 검출될 가능성이 높았던 이들 영역에서 광자의 유무이다.양자적 접근은 Huygens-Fresnel 원리와 몇 가지 두드러진 유사성을 가지고 있습니다; 그 원리에 근거해, 빛이 슬릿과 경계를 통과하면서, 이차, 점 광원은 이러한 장애물들 근처 또는 따라 만들어지고, 결과 회절 패턴은 집합 간섭에 기초한 강도 프로필이 될 것입니다.ll 광로가 다른 광원.이는 양자 형식주의에서 광자가 발생할 가능성이 높은 슬릿과 경계 주변의 제한된 영역을 고려하고 확률 분포를 계산하는 것과 유사하다.이 분포는 고전적 형식주의에서 강도에 정비례합니다.

있습니다. 그것은 한류로부터 파생된 Kirchhoff-Fresnel 회절 방정식 equation,[13]이에 따라 가까운 f에 적용되는 먼 현장 프레넬 회절 근사에 적용되는 키르히호프 방정식의 프라운 호퍼 회절 근사를 포함하는 분산된 필드 계산되는 수 있는 다양한 분석 모델,ield그리고 파인만 경로 적분 공식입니다.대부분의 구성은 해석적으로 해결할 수 없지만 유한 요소 및 경계 요소 방법을 통해 수치적 해법을 산출할 수 있습니다.

개별 2차 파원의 상대적 위상이 어떻게 변화하는지를 고려함으로써 많은 회절 현상에 대한 정성적 이해를 얻을 수 있으며, 특히 위상차가 서로 상쇄되는 사이클의 반에 해당하는 조건을 고려할 수 있다.

회절의 가장 간단한 설명은 상황이 2차원 문제로 축소될 수 있는 것이다.물결의 경우, 이는 이미 해당됩니다. 물결은 수면에서만 전파됩니다.빛의 경우, 회절물체가 파장보다 훨씬 큰 거리를 두고 그 방향으로 뻗어나간다면 우리는 종종 한 방향을 무시할 수 있다.작은 원형 구멍을 통해 빛이 비치는 경우 문제의 완전한 3차원적 특성을 고려해야 합니다.

• 

  직사각형 구멍으로부터의 회절에 의해 스크린에 형성된 컴퓨터 생성 강도 패턴.

• 

  2슬릿 회절에서 간섭 패턴 생성.

• 

  2슬릿 회절 간섭 패턴 계산 모델.

• 

  광학 회절 패턴(레이저), (X선 결정학과 유사)

• 

  일부 분석에 따르면 거미줄에서 보이는 색은 부분적으로 회절 때문이라고 한다.^[14]

예

회절의 영향은 일상생활에서 종종 나타난다.회절의 가장 인상적인 예는 빛을 수반하는 것들이다. 예를 들어 CD나 DVD의 촘촘한 간격의 트랙은 디스크를 볼 때 익숙한 무지개 패턴을 형성하기 위해 회절 격자 역할을 한다.이 원리는 원하는 회절 패턴을 생성할 수 있는 구조를 가진 격자를 설계하도록 확장할 수 있습니다. 신용 카드의 홀로그램이 그 예입니다.작은 입자에 의한 대기 중의 회절은 태양이나 달과 같은 밝은 광원 주변에서 밝은 고리를 볼 수 있게 할 수 있다.단단한 물체의 그림자는 콤팩트한 광원의 빛을 사용하여 가장자리 근처에 작은 테두리를 표시합니다.레이저 빛이 광학적으로 거친 표면에 떨어졌을 때 관찰되는 스펙클 패턴도 회절 현상이다.델리 고기가 무지개빛으로 보일 때, 그것은 고기 ^[15]섬유에서 회절된 것이다.이 모든 효과는 빛이 파장으로 전파된다는 사실의 결과입니다.

회절은 어떤 종류의 파동에서도 발생할 수 있다.바다의 파도는 제트기와 다른 장애물 주변에서 회절된다.음파는 물체 주위로 회절될 수 있고,^[16] 그래서 나무 뒤에 숨어서도 누군가가 부르는 소리를 들을 수 있다.회절은 일부 기술적 응용 분야에서도 문제가 될 수 있습니다. 회절은 카메라, 망원경 또는 현미경의 분해능에 대한 근본적인 한계를 설정합니다.

회절의 다른 예는 다음과 같습니다.

단일 슬릿 회절

빛에 의해 조명되는 극소 폭의 긴 슬릿은 빛을 일련의 원형 파장으로 회절하고 슬릿에서 나오는 파면은 Huygens-Fresnel 원리에 따라 균일한 강도의 원통형 파동이다.

파장보다 넓은 조명 슬릿은 슬릿 하류 공간에 간섭 효과를 발생시킨다.슬릿이 슬릿의 폭에 걸쳐 균등하게 간격을 두고 다수의 점원을 가지는 것처럼 행동한다고 가정하면, 슬릿 간섭 효과를 계산할 수 있다.단일 파장의 빛을 고려한다면 이 시스템의 분석은 간단하다.입사광이 일관성이 있는 경우, 이러한 광원은 모두 같은 위상을 가집니다.슬릿 하류 공간의 특정 지점에서 입사하는 빛은 이러한 각 점 소스로부터의 기여로 구성되며, 이러한 기여의 상대적 위상이 2µ 이상 차이가 나면 회절된 빛에서 최소값과 최대값을 찾을 수 있을 것으로 예상할 수 있다.이러한 위상 차이는 기여하는 광선이 슬릿에서 지점에 도달하는 경로 길이의 차이로 인해 발생합니다.

회절광에서 첫 번째 최소값이 얻어지는 각도는 다음과 같은 추론으로 구할 수 있다.슬릿의 상단 가장자리에 위치한 광원으로부터의 빛은 슬릿의 중간에 위치한 광원과 파괴적으로 간섭하며, 이 광원 간의 경로 차이가 θ/2와 동일할 때 간섭한다.마찬가지로 슬릿 상단 바로 아래의 선원은 동일한 각도로 슬릿 중앙 바로 아래에 위치한 선원과 파괴적으로 간섭합니다.슬릿의 전체 높이를 따라 이 추론을 계속하여 슬릿 전체의 파괴 간섭 조건이 슬릿의 절반 폭인 두 개의 좁은 슬릿 사이의 파괴 간섭 조건과 동일하다는 결론을 내릴 수 있다.경로 차이는 약 ${\displaystyle \frac{d}{}}$ sin ${\displaystyle \frac{}{}}$ ( ${\displaystyle \frac{)}{}}$ )${\displaystyle \frac{\mathrm{}}{}}$ ${$ $displaystyle${ $frac { d$ \ $sin$( \ $theta$ ) }{2$}$}이므로$$ 최소 강도는 다음과 같은 각도로_min 발생합니다.

${\displaystyle d,\sin \theta _{\text{min}}=\displayda }$

어디에

• d는 슬릿의 폭입니다.
• $§$ $min {\displaystyle$ \$theta _{\text{min$}}}은 최소 강도가 발생하는 입사각입니다.
• $§$ $(\displaystyle$ \langda$)$는 빛의 파장입니다.

슬릿이 4개, 6개, 8개 등으로 분할되는 것을 상상하면 다음과 같은 각도로_n 최소값이 구해진다는 것을 나타낼 수 있다.

${\displaystyle d,\sin \theta _{n}=n\displayda}$

어디에

• n은 0 이외의 정수입니다.

우리가 회절 패턴의 최대값을 찾을 수 있게 해주는 그런 간단한 논거는 없다.강도 프로파일은 다음과 같이 프라운호퍼 회절 방정식을 사용하여 계산할 수 있습니다.

$(\displaystyle I(\theta)=I_{0},\operatorname {sinc}^{2}\left({\frac {d\pi}{\lambda}}}\sin \theta \right)}$

어디에

• ${\displaystyle I}$( $)$ ) { $displaystyle$ I ( \ $theta$) }는$$ 주어진 각도의 강도입니다.
• ${\displaystyle {I\mathrm{}}_{}}$ 0$({$은 중심 최대 강도(${\displaystyle }$ ${\displaystyle =}$(\$displaystyle \theta$ = $0)$이며, $또한{\displaystyle }$ {\ ${\displaystyle =}$ - ${\displaystyle \frac{2}{}}$2$(\displaystyle$ \$theta =-{\frac$ \pi }{$2}})$에서 ${\displaystyle =}$ $display$ style 2$(\the$ 2)로의 통합에 의해 결정될 수 있는 강도 프로파일의 정규화 계수이다.}{$2$$}}}$ 및 에너지 절약$.$
• ( ) { sin , x 0 , 0 { $displaystyle$ \$operatorname${$sin }$ ( x $= sin$ { $cases$} { \ $frac$} , &$x$ \ $neq$ 0 \ 1$,$ & x$= 0$ \$end$ { $cases$} the the the 。

이 분석은 원거리 필드(Fraunhofer 회절) 즉, 슬릿 폭보다 훨씬 큰 거리에 있는 경우에만 적용됩니다.

위의 강도 프로파일에서 d ${\displaystyle \mathrm{display}}$ $displaystyle$ d$\ll$ \lambda$$$}$의 경우,$명암$은 $display$ { displaystyle $\theta$${\displaystyle \}<img\; alt="\backslash theta\; "\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/6e5ab2664b422d53eb0c7df3b87e1360d75ad9af"\; style="vertical-align:\; -0.338ex;\; width:1.09ex;\; height:2.176ex;">}$에 거의 의존하지 않습니다.따라서 슬릿에서 발생하는 파면은 방위대칭이 있는 원통형 파도와 유사합니다.$d{\displaystyle }$ \ $displaystyle$ d$\g \lambda$display$$display$$ $displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay$ displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay $display{\displaystyle }$ display display display display display displaydisplaydisplay display display display display display displaydisplay$$\$approx$ 0$}$은 상당한 강도를 가지므로 슬릿에서 발생하는 파면은 기하학적 광학의 파면과 유사합니다$.$

슬릿에 비치는 빛의 입사 각도 ${\displaystyle {\theta }_{}}$ i$\$ _${\text{i}}}$가 0이 아닌 경우(패스 길이 변화를 일으킴), 프라운호퍼 상태(즉, 원거리 필드)의 강도 프로파일은 다음과 같이 됩니다.

$(\displaystyle I(\theta)=I_{0},\operatorname {sinc}^{2}\left[{\frac {d\pi}{\lambda}}}(\sin \theta \sin \theta _{i}\right])$

플러스/마이너스 기호의 선택은 입사각도$$ i \ $displaystyle \theta$ _ { \$text$ { $i$} $\}$ 。

회절 격자

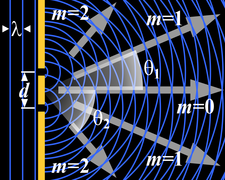
회절격자는 규칙적인 패턴을 가진 광학부품이다.격자에 의해 회절되는 빛의 형태는 요소의 구조와 존재하는 요소의 수에 따라 다르지만, 모든 격자는 격자 방정식에 의해 주어진 각도 θ에서_m 최대 강도를 가진다.

$(*displaystyle d\left(*displaystyle d\sin _{m}}\pm)=m\sin.}$

어디에

• θ는_i 빛이 입사하는 각도입니다.
• d는 격자 요소의 분리이다.
• m은 양의 정수 또는 음의 정수입니다.

격자에 의해 회절되는 빛은 각 요소에서 회절되는 빛의 합계에 의해 발견되며, 기본적으로 회절과 간섭 패턴의 합성입니다.

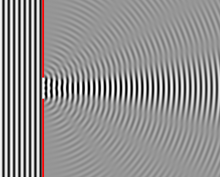
그림에서는 격자 간격이 동일한 2-원소 및 5-원소 격자에 의해 회절되는 빛을 보여 줍니다. 최대값은 같은 위치에 있지만 명암에 대한 자세한 구조는 다릅니다.

원형 개구부

원형 개구부에 입사하는 평면파의 원거리 회절은 에어리 디스크라고 불립니다.각도에 따른 강도 변화는 다음과 같습니다.

$display style$$I_{0}\left({\frac {2J_{1}(ka\sin \theta)}{ka\sin \theta}}}\right$

여기서 a는 원형 개구부의 반지름, k는 2µ/θ, J는₁ 베셀 함수입니다.조리개가 작을수록 일정 거리에서의 스폿 크기가 커지고 회절된 빔의 발산도 커집니다.

일반 개구부

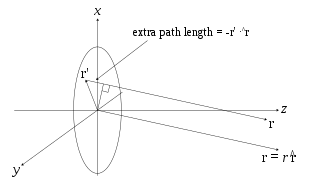
점 소스로부터 발생하는 파형의 위치 r에서의 진폭$\theta {\displaystyle }$(\$displaystyle \psi)$는 점 소스에서의 주파수 영역파 방정식(헬름홀츠 방정식)의 해로 구할 수 있습니다.

$(\displaystyle \mathbf {r}\psi +k^{2}\psi =\displays (\mathbf {r})}$

여기서${\displaystyle }\theta {\displaystyle }$ (${\displaystyle r\mathbf{}}$) \$displaystyle \displaystyle (\mathbf {r}$ )는$$ 3차원 델타 함수입니다.델타 함수는 반지름 의존성만 있으므로 구면 좌표계의 라플라스 연산자(스칼라 라플라스)는 다음과 같이 단순화된다(원통 및 구면 좌표의 델 참조).

${\displaystyle \displayla ^{2}\psi = displayfrac {1}{r} {\frac {{2}} {\frac r^{2}}(r\psi)}$

직접 치환을 통해 이 방정식의 해는 스칼라 그린 함수로 쉽게 나타낼 수 있다. 스칼라 그린 함수는 구 좌표계(및 물리 ${\displaystyle {\mathrm{시간}}^{}}$ 규칙 ${\displaystyle e^{}}$ ${\displaystyle {-}^{}}$ i †$t{\displaystyle {}^{}}$ ${-i\obe$ t$\}$ 사용)에서 다음과 같다.

${\displaystyle \psi (r) = flac {e^{ikr}}{4\pi r}}$

이 솔루션에서는 델타 함수 소스가 원점에 있다고 가정합니다.소스가 벡터 $r{\displaystyle {\mathbf{}}^{}}$ ${\$ {\$displaystyle \mathbf {r}$ '로$$ 표시되는 임의의 소스 포인트에 위치하고 필드 포인트가 r$${\$displaystyle \mathbf {r$ $지점$에 있는 경우 스칼라 그린의 함수를 다음과 같이 나타낼 수 있습니다.

${\displaystyle \psi(\mathbf {r} \mathbf {r} ')=pi \mathbf {r} -\mathbf {r} {4\pi \mathbf {r} -\mathbf {r}}$

따라서 전계 E_inc(x,y)가 개구부에 입사하는 경우, 이 개구 분포에 의해 생성되는 전계는 표면 적분에 의해 주어진다.

${\displaystyle \Psi (r)\propto \limits _{\mathrm {aperture}} E_{\mathrm {inc}(x',y')~{\frac {i\mathbf {r} - {r} {r} - {4\pi \mathbfr} {mathbfr} {r} {mathbf}$

여기서 구멍의 소스 포인트는 벡터에 의해 주어진다.

$\displaystyle \mathbf {r} '=x' \mathbf {x} +y} \mathbf {y}$

평행광선 근사를 사용할 수 있는 원거리장에서는 그린의 함수가

${\displaystyle \psi(\mathbf {r} \mathbf {r} ')=pi \mathbf {r} -\mathbf {r} {4\pi \mathbf {r} -\mathbf {r}}$

으로 심플화

$(\displaystyle \psi (\mathbf {r} \mathbf {r} ') = e^{e^{ikr}}{4\pi r}} e^{-ik(\mathbf {r} '\cdot \mathbf {r}}}}} } )$

오른쪽 그림에서 볼 수 있듯이(클릭하면 확대됩니다).

far-zone (Fraunhofer region) 필드의 식은

$\Psi(r)\propto {e^{ikr}{4\pi r}\iint \limits _{\mathrm {inc}}(x',y)e^{-ik(\mathbf {r}'\cd \mathbf {x}dy}dy$

자, 그 이후로

$\displaystyle \mathbf {r} '=x' \mathbf {x} +y} \mathbf {y}$

그리고.

$\displaystyle \mathbf {r} =\sin \theta \phi {x} +\sin \theta ~\sin \theta {y} +\cos \mathbf {z} }$

평면 개구부에서 프라운호퍼 영역장의 표현은 다음과 같습니다.

$(\displaystyle \Psi(r)\propto {e^{ikr}{4\pi r}}\iint \limits _{\mathrm {inc}}(x',y')e^{-ik\sin \theta (\cos \phi x'+\pi'y')},$

내버려 두는,

${\displaystyle k_{x}=k\sin \theta \cos \phi \,\!}$

그리고.

${\displaystyle k_{y}=k\sin \theta \sin \phi \,\!}$

평면 개구부의 프라운호퍼 영역장은 푸리에 변환의 형태를 띤다

$(\displaystyle \Psi(r)\propto {e^{ikr}{4\pi r}\iint \limits _{\mathrm {aperture}}} E_{\mathrm {inc}}}(x',y')e^{-i(k_{x}x'+k_y})d',$

원계/프라운호퍼 영역에서 이것은 개구 분포의 공간 푸리에 변환이 된다.Huygens의 원리는 단순히 원거리 회절 패턴이 조리개 형상의 공간 푸리에 변환이며, 이것은 조리개 평면장의 평면파 분해를 하는 것과 동일한 평행선 근사 사용의 직접적인 부산물이라고 말한다(푸리에 광학 참조).

레이저 빔의 전파

레이저 빔의 빔 프로파일이 전파되면서 변화하는 방법은 회절에 의해 결정됩니다.방출된 빔 전체가 공간적으로 일관된 평면 파형의 전면을 가지고 있는 경우, 가우스 빔 프로파일에 근사하고 주어진 직경에 대해 가장 낮은 발산을 가집니다.출력 빔이 작을수록 더 빨리 분산됩니다.레이저광의 발산을 저감하려면 먼저 하나의 볼록렌즈로 확대시킨 후 초점과 제1렌즈의 초점이 일치하는 제2볼록렌즈로 시준한다.결과적으로 발생하는 빔의 지름이 더 커지므로 발산도 더 낮아집니다.광강도에 ^[17]따라 전파매체의 굴절률이 증가하면 레이저빔의 발산을 가우스빔의 회절 이하로 감소시키거나 수렴으로 반전시킬 수 있다.이로 인해 셀프 포커싱 효과가 발생할 수 있습니다.

방출된 빔의 파면에 섭동이 있는 경우 레이저 빔의 발산을 결정할 때 가로 방향의 간섭 길이(파장 전면 섭동이 파장의 1/4 미만인 경우)만 가우스 빔 직경으로 간주해야 합니다.수직방향의 횡방향 코히렌스 길이가 수평방향보다 클 경우 레이저광의 발산은 수평방향보다 수직방향에서 낮아집니다.

회절제한 이미징

영상 시스템이 세부 사항을 해결하는 능력은 궁극적으로 회절에 의해 제한됩니다.이는 원형 렌즈나 거울에 입사한 평면파가 위와 같이 회절되기 때문이다.빛은 한 점에 집중되지 않지만 초점 평면에 중심점이 있는 에어리 원반을 형성하며, 이 원반의 반지름은 (첫 번째 null까지 측정)

$\displaystyle \Delta x=1.22\da N}$

여기서 θ는 빛의 파장, N은 이미징 광학의 f-번호(초점 길이 f를 조리개 지름 D로 나눈 값)입니다. 이는 N is1(근축 케이스)에 대해 엄격히 정확합니다.물체 공간에서 대응하는 각도 분해능은

${\displaystyle \theta \approx \sin \theta = 1.22 frac {D},}$

여기서 D는 영상 렌즈의 입구 동공 직경(예: 망원경의 주 거울)입니다.

두 점의 소스는 각각 에어리 패턴을 생성합니다. 쌍성 사진을 참조하십시오.점 소스가 서로 가까이 이동하면 패턴이 겹치기 시작하고 최종적으로 두 점 소스가 병합되어 단일 패턴을 형성합니다. 이 경우 두 점 소스를 이미지에서 확인할 수 없습니다.Rayleigh 기준은 두 영상의 분리가 Airy 디스크의 최소 반지름인 경우, 즉 첫 번째 최소 한 개가 다른 한 개의 최대값과 일치하는 경우 두 개의 점 소스가 "분해된" 것으로 간주하도록 지정합니다.

따라서 파장에 비해 렌즈의 조리개가 클수록 영상촬영 시스템의 해상도가 높아집니다.이것은 천체 망원경이 큰 목표를 필요로 하는 이유 중 하나이며, 왜 현미경 목표물은 가능한 한 최고의 해상도를 얻기 위해 큰 숫자 구멍(작업 거리 대비 큰 구멍 직경)을 필요로 하는가이다.

스펙클 패턴

레이저 포인터를 사용할 때 나타나는 반점 패턴도 회절 현상입니다.이는 레이저 빔이 거친 표면을 비추면 생성되는 서로 다른 상으로 된 많은 파동이 중첩된 결과입니다.그것들은 합쳐져서 진폭과 강도가 무작위로 변화하는 결과적인 파동을 만들어냅니다.

바비넷의 원리

바비넷의 원리는 불투명한 물체의 회절 패턴이 크기와 모양이 같은 구멍의 회절 패턴과 동일하지만 강도가 다르다는 유용한 정리이다.즉, 단일 장애물의 간섭 조건은 단일 슬릿의 간섭 조건과 동일합니다.

"칼끝"

칼끝 효과 또는 칼끝 회절은 산맥이나 건물의 벽과 같이 명확하게 정의된 날카로운 장애물에 부딪히는 입사 방사선의 일부를 잘라낸 것이다.칼끝 효과는 전자파에 대한 잘 정의된 방해물이 2차 선원으로 작용하여 새로운 파면을 만든다는 Huygens-Fresnel 원리에 의해 설명된다.이 새로운 파면은 장애물의 기하학적 그림자 영역으로 전파됩니다.

칼끝 회절은 원래 아놀드 소머펠트가 평면파 스펙트럼 공식을 사용하여 해결한 "반면 문제"의 산물이다.반평면 문제의 일반화는 원통 좌표의 경계값 문제로 해결할 수 있는 "웨지 문제"입니다.원통 좌표의 해는 조셉 B에 의해 광학계까지 확장되었다. 켈러는 그의 기하학적 회절 이론(GTD)을 통해 회절 계수의 개념을 도입했다.파탁과 쿠유엠지안은 균일한 회절 이론(UTD)을 통해 켈러 계수를 확장했습니다.

• 

  날카로운 금속 모서리의 회절

• 

  이미지 폭에 걸쳐 전도율의 구배를 갖는 부드러운 개구부의 회절

패턴

일반적으로 회절에는 다음과 같은 몇 가지 정성적 관찰을 할 수 있다.

• 회절 패턴의 특징의 각도 간격은 회절을 일으키는 물체의 치수에 반비례합니다.즉, 다음과 같습니다.회절물체가 작을수록 회절패턴이 '감겨'지고, 그 반대도 마찬가지입니다. (더 정확히 말하면, 이것은 각도의 사인(sine)에 해당됩니다.)
• 회절각은 스케일링 하에서는 불변합니다.즉, 회절각은 회절물체의 크기에 대한 파장의 비율에만 의존합니다.
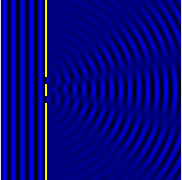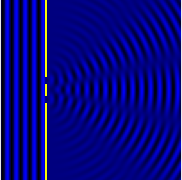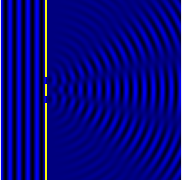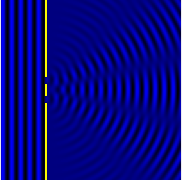
• 회절격자 등 회절물체가 주기적인 구조를 가지고 있는 경우 일반적으로 형상이 더 선명해집니다.예를 들어, 세 번째 그림은 5개의 슬릿으로 이루어진 패턴과 이중 슬릿 패턴을 비교한 것으로, 두 슬릿의 중심과 다음 슬릿 사이의 간격이 같은 슬릿 세트입니다.

입자 회절

양자 이론에 따르면 모든 입자는 파동 특성을 보인다.특히, 무거운 입자는 스스로 간섭할 수 있고, 따라서 회절할 수 있다.전자와 중성자의 회절은 양자역학을 지지하는 강력한 주장 중 하나였다.입자와 관련된 파장은 드 브로글리 파장이다.

$\displaystyle \displayda = displayfrac {h}{p}},$

여기서 h는 플랑크의 상수이고 p는 입자의 운동량이다(느린 입자의 경우 질량×속도).

대부분의 거시적 물체의 경우 이 파장은 너무 짧기 때문에 파장을 할당하는 것은 의미가 없습니다.약 30,000m/s로 이동하는 나트륨 원자는 약 50피코미터의 드 브로글리 파장을 가집니다.

가장 작은 거시적 물체의 파장이 매우 작기 때문에 물질파의 회절은 전자, 중성자, 원자, 그리고 작은 분자와 같은 작은 입자에 대해서만 볼 수 있습니다.이러한 물질파의 짧은 파장은 단백질과 같은 고체와 큰 분자의 원자 결정 구조를 연구하는데 이상적으로 적합하게 만든다.

버키볼과 같은 비교적 큰 분자들도 ^[18]회절하는 것으로 나타났다.

브래그 회절

결정의 원자와 같은 3차원 주기 구조로부터의 회절은 브래그 회절이라고 불립니다.이는 회절격자에서 파동이 산란될 때 발생하는 것과 유사합니다.브래그 회절은 다른 결정면에서 반사되는 파동 사이의 간섭의 결과입니다.건설적 간섭 조건은 브래그의 법칙에 의해 제시된다.

${\displaystyle m\sinda = 2d\sin \theta }$

어디에

• θ는 파장이고,
• d는 결정면 사이의 거리이다.
• θ는 회절파의 각도입니다.
• m은 회절된 빔의 순서로 알려진 정수입니다.

브래그 회절은 X선처럼 파장이 매우 짧은 전자파나 파장이 원자 ^[19]간격에 가까운 중성자(및 전자)와 같은 물질파를 사용하여 수행될 수 있다.생성된 패턴은 결정면 d의 분리 정보를 제공하므로 결정 구조를 추론할 수 있습니다.특히 전자현미경 및 x-topography 디바이스에서 회절 대비는 결정의 개별 결함과 국소 변형률장을 검사하는 강력한 도구이기도 합니다.

일관성

회절의 설명은 같은 소스에서 나오는 파동이 화면상의 같은 포인트로 다른 경로를 통과하는 간섭에 의존합니다.이 설명에서 서로 다른 경로를 통과한 파동 간의 위상 차이는 유효 경로 길이에 따라 달라집니다.이는 동시에 화면에 도달하는 파동이 다른 시간에 발생원에 의해 방출된다는 사실은 고려하지 않는다.소스가 파동을 방출하는 초기 위상은 시간에 따라 예측할 수 없는 방식으로 변경될 수 있습니다.즉, 위상 간의 관계가 더 이상 시간에 ^{[20]: 919} 의존하지 않기 때문에 너무 멀리 떨어져 있을 때 소스로부터 방출되는 파형이 더 이상 일정한 간섭 패턴을 형성할 수 없습니다.

광선의 위상이 상관되는 길이를 코히렌스 길이라고 합니다.간섭이 발생하려면 경로 길이 차이가 간섭 길이보다 작아야 합니다.이것은 파동에 다른 주파수 성분이 존재하는 것과 관련이 있기 때문에 스펙트럼 코히렌스라고 불리기도 한다.원자 천이에 의해 방출되는 빛의 경우, 코히렌스 길이는 원자가 ^{[21]: 71–74 [22]: 314–316} 천이를 한 들뜬 상태의 수명과 관련된다.

확장된 소스에서 파동이 방출되면 횡단 방향의 일관성이 저하될 수 있습니다.광선의 단면을 볼 때, 위상이 상관되는 길이를 횡단 코히렌스 길이라고 합니다.영의 이중 슬릿 실험의 경우, 이는 가로 방향의 코히렌스 길이가 두 슬릿 사이의 간격보다 작을 경우 스크린의 결과 패턴이 두 개의 단일 슬릿 회절 ^{[21]: 74–79} 패턴처럼 보인다는 것을 의미합니다.

전자, 중성자, 원자와 같은 입자의 경우, 일관성 길이는 ^{[23]: 107} 입자를 설명하는 파동 함수의 공간적 범위와 관련이 있습니다.

적용들

파괴 전 회절

X선 자유 전자 레이저에 의해 생성된 밝은 X선을 이용하여 지난 몇 년 동안 단일 생물학적 입자를 촬영하는 새로운 방법이 등장했다.이러한 펨토초 지속 펄스는 단일 생물학적 고분자의 (잠재적) 이미징을 허용합니다.이러한 짧은 펄스로 인해 방사선 손상을 능가할 수 있으며 단일 생물학적 고분자의 회절 패턴을 ^[24][25]얻을 수 있습니다.

「 」를 참조해 주세요.

레퍼런스

외부 링크

• 물리학에 관한 파인만 강의 제1권.I장 30: 회절
• "Scattering and diffraction". Crystallography. International Union of Crystallography.