지그재그 보조정리

수학, 특히 호몰로지 대수학에서 지그재그 보조마사는 특정 연쇄 복합체의 호몰로지 집단에서 특정 긴 정확한 순서의 존재를 주장한다.그 결과는 모든 아벨의 범주에서 유효하다.

성명서

In an abelian category (such as the category of abelian groups or the category of vector spaces over a given field), let $({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')$ and ${\displaystyle ({\mathcal {C}},\partial _{\bullet }'$ $')}$ 은(는) 다음과 같은 짧은 정확한 순서에 맞는 체인 콤플렉스들이다 $({\mathcal {C}},\partial _{\bullet }'')$ .

0\longwrightarrow {\mathcal {A}\mathrel {\longwrightarrow}}{\\mathcal {B}\longwrightarrow {\\stackrel {\beta}}}}{\mathc}\long rigrowardarrow}}

이러한 순서는 다음과 같은 대응 도표의 속기법이다.

여기서 행은 정확한 시퀀스이고 각 열은 체인 콤플렉스다.

지그재그 보조정리자는 경계 지도의 집합이 있다고 주장한다.

\property_{nH_{n}({\mathcal {C})\긴 오른쪽 화살표 H_{n-1}({\mathcal {A}),

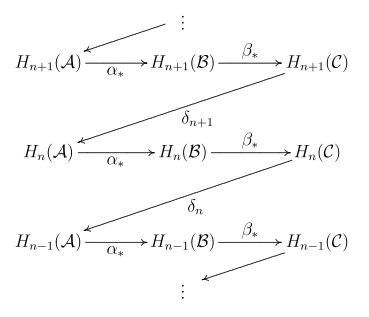
다음과 같은 순서를 정확하게 한다.

지도 $\alpha _{*}^{}$ $displaystyle \alpha _{*}^{}}$ 및 $\alpha _{*}^{}$ $\beta _{*}^{}$ $\beta _{*}^{}$ $displaystyle \beta _{*}^{}}}}}}$ 는 $\beta _{*}^{{}}$ 호몰로학에 의해 유도된 일반적인 지도들이다.경계 지도 $\delta _{n}^{}$ $displaystyle \delta _{n}^{}}}{}}}}}$ 은(는) 아래에 설명되어 $\delta _{n}^{}$ 있다.보조정리자의 이름은 순서에 따라 지도의 "지그재그" 동작에서 비롯된다.지그재그 보조마마의 변형 버전은 흔히 "뱀 보조마"라고 알려져 있다(이것은 아래에 제시된 지그재그 보조마 증거의 진수를 추출한다).

경계지도 작성

맵 $\delta _{n}^{}$ $displaystyle \delta_{n}^{}}}}}$ 은(는) 표준 다이어그램 추적 인수를 사용하여 정의된다 $\delta _{n}^{}$ .Let $c\in C_{n}$ represent a class in $H_{n}({\mathcal {C}})$ , so $\partial _{n}''(c)=0$ . Exactness of the row implies that $\beta _{n}^{}$ is surjective, so there must be some ${\di$ $\beta _{n}^{}(b)=c$ $\beta _{n}^{}(b)=c$ ) $\beta _{n}^{}(b)=c$ = $\beta _{n}^{}(b)=c$ ${\displaystyle \b_{$ $n$ }^{ $n}{n}=c}$ 을 $\beta _{n}^{}(b)=c$ 를) 포함한 $b\in B_{n}$ $splaystyle b\in B_$ {n $}.$ 도표의 동일성에 따라,

\property_{n-1}\pair_{n}(b)=\pair_{n}\pair_{n}=0.

정확히 말하자면

\displaystyle \property \n'(b)\in \ker \protection_{n-1}=\mathrm {im} \protection_{n-1}.}

Thus, since $\alpha _{n-1}^{}$ is injective, there is a unique element $a\in A_{n-1}$ such that $\alpha _{n-1}(a)=\partial _{n}'(b)$ . $\alpha _{n-2}^{}$ - $\alpha _{n-2}^{}$ $displaystyle \alpha _{n-2}^{}}}}}}$ 이(가) 주입식이고 $\alpha _{n-2}^{}$ , 또 주입식이기 때문에 이것은 순환이다.

\cHB_{n-2}\cHB_{n-1(a)=\cHB_{n-1(a)=\cHB_{n-1(a)=\cHB_{n1}(b)=0,

$\partial ^{2}=0$ $\partial ^{2}=0$ = $\partial ^{2}=0$ 0 {\ $displaystyle \filename ^{$ 2}= $0}$ 이후 $\partial ^{2}=0$ That is, $\partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}$ . This means $a$ is a cycle, so it represents a class in $H_{n-1}({\mathcal {A}})$ . We can now define