비비아니의 정리

빈첸초 비비아니의 이름을 딴 비비아니의 정리는 어느 내부 지점에서 정삼각형의 옆면까지의 거리의 합이 삼각형의 고도 길이와 같다고 명시하고 있다.^[1] 각종 수학 경시대회, 중등부 수학 시험에서 흔히 쓰이는 정리로서 현실의 많은 문제들에 폭넓게 적용이 가능하다.

증명

이 증거는 삼각형의 면적이 그것의 키의 절반, 즉 그 쪽에서 고도가 있는 한쪽의 생산물의 절반이라는 쉽게 입증된 명제에 달려 있다.^[2]

ABC는 높이가 h이고 옆면이 a인 등변 삼각형이 되도록 하자.

P는 삼각형 안에 있는 어떤 점이고, u, s는 측면으로부터 P의 거리를 두도록 한다. 3개의 삼각형 PAB, PBC, PCA를 형성하여 P에서 A, B, C 각각으로 선을 그린다.

현재 이 삼각형의 영역은 ${\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{\cdot }{}}$ ${\displaystyle \frac{2}{}}$ ${\$ a$}{2$ ${\displaystyle \frac{\mathrm{}}{}}${ 2 ${\$s\$cdot$ a$\},$ ${$ 2 ${\frac{t\cdot$ a$}}{2$ 그것들은 정확히 둘러싸인 삼각형을 채우기 때문에, 이들 영역의 합은 둘러싸인 삼각형의 면적과 같다. 그래서 우리는 다음과 같이 쓸 수 있다.

${\displaystyle {\frac {u\cdot a}{2}}+{\frac {s\cdot a}{2}}+{\frac {t\cdot a}{2}}={\frac {h\cdot a}{2}}}}}$

따라서

${\displaystyle u+s+t=h}$

Q.E.D.

컨버스

역은 또한 다음과 같다: 삼각형의 내부 지점에서 옆면까지의 거리의 합이 점의 위치와 독립된 경우, 삼각형은 정사각형이다.^[3]

적용들

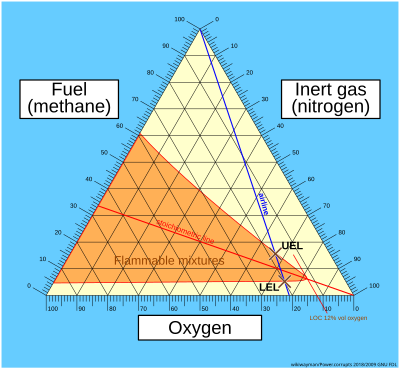
비비아니의 정리란 등변 삼각형의 측면에 평행한 선들이 가연성 도표와 같은 3차 플롯을 만들기 위한 좌표를 제공한다는 것을 의미한다.

보다 일반적으로, 그들은 같은 방법으로 일반 심플렉스에서의 좌표를 제공할 수 있다.

확장

평행사변형

평행사변형의 내부점으로부터 측면까지의 거리의 합은 점의 위치와 무관하다. 반대는 또한 다음과 같다: 4각형 내부의 한 지점에서 옆면까지의 거리의 합이 점의 위치와 무관하다면, 4각형은 평행사변형이다.^[3]

결과는 반대쪽이 평행한 2n-곤으로 일반화된다. 어느 한 쌍의 반대쪽 평행선 사이의 거리의 합은 일정하므로, 평행선 쌍 사이의 모든 쌍별 합계의 합도 일정하다는 것을 따른다. 그 결과는 반드시 반대편이 평행하지 않은 등변 육각형을 유지하므로 일반적으로 정반대되는 것은 아니다.

정규 다각형

다각형이 정규적인 경우(등각형 및 등각형 모두) 내부 점에서 측면까지의 거리의 합은 점의 위치와 무관하다. 구체적으로는 아포템의 n배와 같으며, 여기서 n은 면의 수, 아포템은 중앙에서 측면까지의 거리가 된다.^[3][4] 그러나 그 반대는 유지되지 않는다. 비제곱 평행사변형은 counterrexample이다.^[3]

등각 다각형

내부 점에서 등각 다각형의 측면까지의 거리의 합은 점의 위치에 따라 달라지지 않는다.^[1]

볼록 폴리곤

볼록 폴리곤이 어떤 내부 지점에서 옆면까지의 거리의 일정한 합을 갖기 위해 필요하고 충분한 조건은 동일한 거리를 가진 세 개의 비접합 내부 점이 존재한다는 것이다.^[1]

정다면체

일반 다면체 내부의 임의 지점부터 측면까지의 거리의 합은 점의 위치와 무관하다. 그러나, 4면체도 아닌, 그 반전은 유지되지 않는다.^[3]

참조

추가 읽기

• Gueron, Shay; Tessler, Ran (2002). "The Fermat-Steiner problem". Amer. Math. Monthly. 109 (5): 443–451. doi:10.2307/2695644. JSTOR 2695644.
• Samelson, Hans (2003). "Proof without words: Viviani's theorem with vectors". Math. Mag. 76 (3): 225. doi:10.2307/3219327. JSTOR 3219327.
• Chen, Zhibo; Liang, Tian (2006). "The converse of Viviani's theorem". The College Mathematics Journal. 37 (5): 390–391.
• Kawasaki, Ken-Ichiroh; Yagi, Yoshihiro; Yanagawa, Katsuya (2005). "On Viviani's theorem in three dimensions". Math. Gaz. 89 (515): 283–287. JSTOR 3621243.
• Zhou, Li (2012). "Viviani polytopes and Fermat Points". Coll. Math. J. 43 (4): 309–312. arXiv:1008.1236. CiteSeerX 10.1.1.740.7670. doi:10.4169/college.math.j.43.4.309.

외부 링크

• Weisstein, Eric W. "Viviani's Theorem". MathWorld.
• 리주, 비비안니 폴리토페스, 페르마트 포인트
• "Viviani's Theorem: What is it?". 결혼식에서.
• Warendorff, Jay. "Viviani's Theorem". 울프램 데모 프로젝트
• "A variation of Viviani's theorem & some generalizations". 대화형 동적 지오메트리 스케치인 동적 지오메트리 스케치
• Abboud, Elias (2017). "Loci of points inspired by Viviani's theorem". arXiv:1701.07339 [math.HO].
• Armstrong, Addie; McQuillan, Dan (2017). "Specialization, generalization, and a new proof of Viviani's theorem". arXiv:1701.01344 [math.HO].