밀도(폴리토프)

Density (polytope)
일반 에네그램 {9/4}의 경계는 중심 주위를 4번 돌기 때문에 밀도가 4이다.

기하학에서 항성 다면체의 밀도는 다면체의 대칭 중심 주위에 있는 다면체의 권선 수를 나타내는 2차원에서 더 높은 차원으로의 권선수의 개념을 일반화한 것이다.중심에서 무한대로 광선을 통과시키고, 어떤 저차원적 특징을 통과하지 않고 폴리토프의 면만을 통과하며, 얼마나 많은 면들을 통과하는지 세어 보면 알 수 있다.이 카운트가 광선의 선택에 의존하지 않고 중심점이 어떤 면에도 의존하지 않는 다면체의 경우, 이 교차 면의 카운트에 의해 밀도가 주어진다.

대칭이 없는 볼록한 다면체에도 동일한 계산을 수행할 수 있으며, 다면체의 어느 점 내부를 중심점으로 선택함으로써 대칭이 없는 다면체에도 동일한 계산을 수행할 수 있다.이 다면체의 경우 밀도는 1이 될 것이다.보다 일반적으로 비자체간격(아콤프틱) 다면체의 경우, 다면체의 면만 통과하는 내부 지점에서 광선을 선택하고 이 광선이 다면체의 내부에서 외부로 통과할 때 광선을 추가하고 이 광선이 다면체의 외부로 통과할 때 광선을 빼는 유사한 계산에 의해 밀도를 1로 계산할 수 있다.다면체 내부의 외부그러나 이러한 교차로의 표지의 배정은 일반적으로 별 다면체에는 적용되지 않는데, 이는 내·외부가 잘 정의되어 있지 않기 때문이다.

얼굴이 겹치는 테셀레이션은 주어진 포인트에 걸쳐 면의 커버링 수로 밀도를 유사하게 정의할 수 있다.[1]

폴리곤

다각형의 밀도는 다각형의 경계가 중심 주위를 감는 횟수를 말한다.볼록한 폴리곤과 보다 일반적으로 간단한 폴리곤의 경우(자기간섭이 아님), 조던 곡선 정리상 밀도는 1이다.

폴리곤의 밀도는 그것의 회전수라고도 불릴 수 있다; 모든 정점의 회전각의 합을 360°로 나눈다.이것은 평면의 모든 유니쿠르 경로에 대한 정수가 될 것이다.

복합 폴리곤의 밀도는 성분 폴리곤의 밀도를 합한 것이다.

일반 항성 다각형

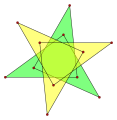
일반 항성 폴리곤 {p/q}의 경우 밀도는 q이다.중심에서 무한대로 광선의 최소 에지 교차 수를 세어 시각적으로 결정할 수 있다.

예

폴리헤드라

다면체와 그것의 이중은 같은 밀도를 가지고 있다.

총곡률

다면체는 정점에 집중되고 각도 결함으로 정의되는 가우스 곡면성을 가진 표면으로 간주할 수 있다.다면체의 밀도는 총 곡률(정점 전체에 걸쳐 포함)을 4㎛로 나눈 값과 같다.[2]

예를 들어, 큐브에는 각각 3개의 정사각형이 있는 8개의 정점이 있어 ,/2. 8××/2=44의 각도 결함을 남긴다.그래서 큐브의 밀도는 1이다.

단순다면체

단순한 얼굴과 정점 형상을 가진 다면체의 밀도는 오일러 특성 χ의 절반이며, 그 속성이 g이면 밀도는 1g이다.

χ = V - E + F = 2D = 2(1-g)

  • 위상구 다면체의 밀도는 큐브와 같다.
    v=8, e=12, f=6

  • 1 토로이드 다면체의 밀도는 이 육각형 형태와 같이 0이다.
    v=24, e=48, f=24.

  • 5 toroidal 속 밀도는 -4이다. 이 Stewart_toroid:
    v=72, e=18, f=88.

항성 다면체

아서 케일리는 오일러의 다면체 공식(V - E + F = 2)을 수정하여 일반 별 다면체에서 작용하는 방법으로 밀도를 사용했는데, 여기서 d는v 정점 형상의 밀도f, 얼굴 d, 다면체 전체의 D이다.

[3]

예를 들어, 위대한 이코사헤드론 {3, 5/2}은 20개의 삼각면(df = 1)과 30개의 가장자리, 12개의 오각정점 그림(dv = 2)을 가지고 있다.

2·12 − 30 + 1·20 = 14 = 2D.

이것은 7의 밀도를 의미한다.수정되지 않은 오일러의 다면체 공식은 작은 나선형 도면체 {5/2, 5} 및 그 이중 대면체 {5, 5/2}에 대해 실패하며, V - E + F = -6.

일반 항성 다면체는 두 쌍으로 존재하며, 각 형상은 두 쌍과 동일한 밀도를 가진다: 한 쌍(소형 도면체-대면체)은 밀도가 3이고, 다른 한 쌍(대면체-대면체)은 밀도가 7이다.

Great icosahedron.png Great icosahedron cutplane.png
비콘벡스 대 이코사면체, {3,5/2}은(는) 오른쪽의 이 투명하고 단면적인 시야에서 보여지듯이 밀도가 7이다.

일반성 다면체

에드먼드 헤스는 다른 종류의 얼굴을 가진 별 다면체의 공식을 일반화했는데, 그 중 일부는 다른 것들보다 뒤로 접힐 수도 있다.밀도에 대한 결과 값은 연관된 구형 다면체가 구를 덮는 횟수에 해당한다.

이를 통해 Coxeter 등은 하나의 꼭지점 유형과 여러 개의 얼굴 유형을 갖는 균일한 다면체의 대다수의 밀도를 결정할 수 있었다.[4]

  • 두 번 포장된 팔각 프리즘의 밀도는 2, {8/2}×{}}이며, 선명도를 위해 오프셋 정점과 함께 여기에 표시된다.
    v=16, e=24
    f1=8 {4}, f2=2 {8/2}
    df1=1, df2=2, dv=1로

  • 펜타그램 프리즘, {5/2}×{}의 밀도는 2이다.
    v=10, e=15,
    f1=5 {4}, f2=2 {5/2},
    df1=1, df2=2.

비방향성 다면체

얼굴 일부가 중앙을 통과하는 혈중수면체의 경우 밀도를 정의할 수 없다.방향성이 없는 다면체도 밀도가 잘 정의되지 않는다.

일반 4폴리톱

그 거대한 120개의 셀은 밀도 191을 가지고 있다.

일반별 4폴리탑(Schléfli–Hess 4폴리탑이라고 함)은 10개로, 밀도는 4, 6, 20, 66, 76, 191이다.이 값은 자체 이중 밀도-6과 밀도-66 수치를 제외하고 이중 쌍으로 나온다.

메모들

  1. ^ Coxeter, H. S. M; 기하학의 아름다움: 12편의 에세이(1999년), 도버 출판사, LCCN99-35678, ISBN0-486-40919-8(206–214, 쌍곡선 공간의 일반 벌집 밀도)
  2. ^ 미니애폴리스 17의 기하학과 상상력다면체의 각도 결함; 20.표면의 곡률, 21.가우스 곡률; 다면체의 경우 27.3.1 곡률 페이지 32-51
  3. ^ Cromwell, P.; P.; Polyedra, CUP hbk(1997), PB.(1999).(258쪽)
  4. ^ Coxeter, 1954 (섹션 6, 밀도 및 표 7, 균일한 다면체)

참조

외부 링크