스너브 디스페노이드

스너브 디스페노이드
유형	존슨 J83 - J84 - J85
얼굴	4+8 삼각형
가장자리	18
정점	8
꼭지점 구성	4(34) 4(35)
대칭군	D2d
이중 다면체	길쭉한 교비파스티기움
특성.	볼록한 삼각면
그물

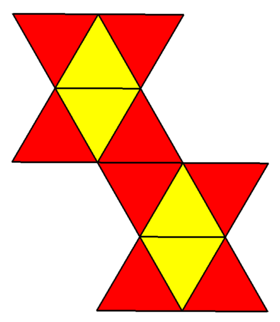기하학에서 스너브 디스페노이드, 샴 도데카헤드론, 삼각 도데카헤드론, 삼각 도데카헤드론 또는 도데카데타헤드론은 12개의 정삼각형을 면으로 하는 3차원 볼록 다면체다.어떤 정점은 4개의 얼굴을 가지고 있고 다른 정점은 5개의 얼굴을 가지고 있기 때문에 일반 다면체는 아니다.도데카헤드론이며, 8개의 델타헤드라(등각 삼각면이 있는 콘벡스 다면체) 중 하나와 92개의 존슨 고형물(정규면이 있는 비통일 볼록 다면체) 중 하나이다.양쪽 정사각형이 모두 정삼각형 두 개로 대체되는 정사각형 항정신병이라고 생각할 수 있다.

스너브 디스페노이드도 이등분 13-5계단 프리즘의 정점형상으로, 3각형의 정점을 선택한 후 다음 삼각형의 5번째 정점을 선택하여 원래의 삼각형에 도달할 때까지 그렇게 하는 13-13 두오프리즘으로, 원래의 삼각형에 도달할 때까지 그렇게 한다.그러나 스너브 디스페노이드에는 구형이 없기 때문에 균일하게 만들 수 없다.

기록 및 이름 지정

이 모양은 한스 프로이덴탈과 B. L. 반 데어 바어든(1947)에 의해 논문에서 샴 도데카헤드론이라고 불렸는데, 이것은 8개의 볼록 델타헤드라의 집합을 처음 묘사하였다.^[1]도데카델타헤드론 이름은 베르날(1964년)이 12면 삼각주라는 사실을 언급하면서 같은 모양으로 붙여졌다.육각형 bipyramid 등 다른 단순화된 도데카헤드라가 있지만, 정각형 얼굴로 실현 가능한 것은 이것뿐이다.베르날은 불규칙하게 촘촘히 박혀 있는 구들의 배열 속에 남아 있는 구멍의 모양에 관심이 있었기 때문에 델타헤드라의 제한적인 정의를 사용했는데, 델타헤드론은 삼각형의 얼굴을 가진 볼록한 다면체로서, 접선성은 다면체의 가장자리를 나타내는 응집체의 중심에 의해 형성될 수 있는 형태다면체다, 그와 같은 형태다면체이다.이 구체 체계에 의해 만들어진 우리 안에 또 다른 구체를 포장할 공간이 없다.이러한 제한적 정의는 삼각형 비피라미드(단일 구멍보다는 사면 구멍을 두 개 형성하는 것), 오각형 비피라미드(정점을 위한 구들이 서로 교차하기 때문에 구 포장에서 발생할 수 없기 때문에), 이코사헤드론(다른 구를 위한 내부 공간이 있기 때문에)을 허용하지 않는다.베르날은 스너브 디스페노이드(snub dispenoid)가 "결정학상 칼슘 이온에 대한 매우 일반적인 조정"이라고 쓰고 있다.^[2]조정 기하학에서는 보통 삼각 도두면체 또는 간단히 도두면체라고 알려져 있다.

스너브 디스페노이드 이름은 노먼 존슨이 1966년 존슨의 고형분인 볼록 폴리아드라를 분류한 것에서 유래했다.^[3]축대칭이 있는 일련의 다면체에서 먼저 존재하기 때문에 디간론 자이로비안티쿠폴라라는 이름도 붙일 수 있다.

특성.

스너브 디스페노이드(snub disphenoid)는 4개의 정점을 제거하여 나머지 정점을 분리해야 한다는 것을 의미한다.그것은 단지 4개의 4개의 연결로 잘 덮인 다면체 중 하나로서, 그것의 정점의 모든 최대 독립된 세트의 크기가 같다는 것을 의미한다.이 성질을 가진 나머지 3개의 다면체는 정팔면체, 오각형 쌍면체, 12개의 정점과 20개의 삼각면을 가진 불규칙 다면체다.^[4]

스너브 디스페노이드(snub dispenoid)는 4각형 디스페노이드와 동일한 대칭을 가지고 있다. 대칭은 반대쪽 두 가장자리의 중간점을 통과하는 180° 회전 대칭의 축을 가지고 있으며, 이 축을 통한 반사 대칭의 수직면 2개, 그리고 1/4회전 뒤에 축에 수직으로 반사되어 주어지는 4개의 추가 대칭 연산을 가지고 있다.축과 평행한 또 다른 반사일 수 있다.^[5]즉, 순서 8의 대칭군인 D항정_2d 대칭을 가지고 있다.

스너브 디스페노이드의 정점에 중심을 둔 구들은, 수치 실험에 따르면, 모든 8-sphere 클러스터 중에서 가능한 최소의 레나드 존스를 가진 군집을 형성한다.^[6]

대칭 및 병렬 번역까지 스너브 디스페노이드에는 5가지 유형의 단순(자체 교차하지 않는) 폐쇄형 지오디지오데틱이 있다.이것들은 정점을 피하고 국소적으로 최단 경로처럼 보이는 다면체의 표면에 있는 경로들이다: 그들은 그들이 교차하는 다면체의 각 면에 걸쳐 직선 세그먼트를 따르고, 그것들이 다면체의 가장자리를 가로지르면 두 개의 입사 면에 가장자리까지 상호보완적인 각도를 만든다.직관적으로, 이 길을 따라 다면체 주위에 고무줄을 둘 수 있고 그것은 제자리에 머물 것이다: 국소적으로 경로를 변경하고 길이를 짧게 할 수 있는 방법은 없다.예를 들어, 한 유형의 지오데틱은 중간점(대칭 축이 폴리토페에서 나가는 곳)에서 스너브 디스페노이드의 두 반대쪽 가장자리를 crosses/3의 각도로 교차한다.두 번째 유형의 지오데닉은 대칭 축(다면체의 적도)을 수직으로 이등분하는 면과 스너브 디스페노이드의 교차점 부근을 통과하여 π/2와 π/6을 교대하는 각도로 8개의 삼각형의 가장자리를 교차한다.다면체 표면의 지오데틱을 소량(이동 때문에 정점이 교차하지 않을 정도로 작음)으로 이동하면 지오데틱으로서의 특성을 보존하고 길이를 보존하기 때문에 이 두 예 모두 대칭적으로 배치되지 않은 동일한 유형의 버전을 이동시켰다.단위 길이 가장자리가 있는 스너브 디스페노이드에 있는 5개의 단순 닫힌 지오디컬의 길이는 다음과 같다.

${\displaystyle 2{\sqrt {3}}\approx 3.464}$ (for the equatorial geodesic), ${\displaystyle {\sqrt {13}}\approx 3.606}$, ${\displaystyle 4}$ (for the geodesic through the midpoints of opposite edges), ${\displaystyle 2{\sqrt {7}}\approx 5.292}$, and ${\disp$$레이스타일 {\sqrt{19}\$ 약 $4.359$

스너브 디스페노이드에는 단순 폐쇄형 ^[7]지오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오데오

건설

스너브 디스헤노이드(snub disphenoid)는 이름에서 알 수 있듯이 일반 사면체의 낮은 대칭 형태인 사면체에서 형성된 스너브 다면체(snub polyheadron)이다.

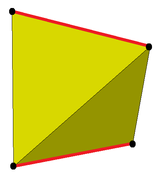디스페노이드	스너브 디스페노이드

스너브 연산은 두 개의 반대쪽 가장자리(그림에서 빨간색)와 인접한 삼각형을 분리하는 단일 주기적 삼각형 띠를 생성한다.스너브 반격은 단일 주기적인 삼각형 띠를 갖는다는 점에서 유사하지만, 스너브 반대편에서 이 띠들은 두 개의 반대쪽 가장자리가 아닌 두 개의 반대쪽 면과 인접한 삼각형을 분리한다.

스너브 디스페노이드도 정삼각형 쌍으로 두 개의 정사각형 면을 대체함으로써 정사각형 항정신병으로부터 형성될 수 있다.그러나 이것은 플라토닉과 아르키메데스 고형물의 "잘라서 붙여넣기" 조작에서 생기지 않는 기본적인 존슨 고형물 중 하나이다.

스너브 디스페노이드의 물리적 모델은 표시된 12개의 등변 삼각형 (12-iamond)으로 형성된 그물을 접어서 형성할 수 있다.존 몬트롤이 제시한 대안적 그물은 그 경계선에 오목한 꼭지점이 적어 종이접기 제작에 더욱 편리하다.^[8]

데카르트 좌표, 평행 좌표.

$q{\displaystyle 0}$ 0.${\displaystyle 16902}$ ${\displaystyle q\ 약$ 0.$16902}$을(를) 입방 다항식의 양의 실제 루트가 되도록$$ 한다.

${\displaystyle 2x^{3}+11x^{2}+4x-1.}$

더 나아가자.

${\displaystyle r={\sqrt{q}\약 0.41112,}$

${\displaystyle s={\sqrt {\frac {1-q}{2q}}\약 1.56786,}$

그리고

${\displaystyle t=2rs={\sqrt{2-2q}\약 1.28917.}$

스너브 디스페노이드의 8개 꼭지점에 데카르트 좌표가 주어질 수 있다.

${\displaystyle(\pm t,r,0),\,(0,-r,\pm t),}$

$[\displaystyle(\pm 1,-s,0),\,(0,s,\pm 1)]}$^[6]

이 구조는 입방정식에 대한 해답을 포함하기 때문에 다른 7개의 델타헤드라와 달리 나침반과 직선으로 스너브 디스페노이드(snub disphenoid)를 구성할 수 없다.^[9]

이러한 좌표를 사용하면 가장자리 길이가 $a$인 스너브 디스페노이드의 볼륨을 ${\displaystyle {3\mathrm{}}^{}}$ ${\$ a$^{3}$로 계산할 수 있으며$,$ 여기서 $\xi {\displaystyle }$ ${\displaystyle \approx }$ ${\displaystyle 0.85949}$ ${\displaystyle \xi$ \sxi $\약 0.859}$은$$다항식의 양의 루트다.

${\displaystyle 5832x^{6}-1377x^{4}-2160x^{2}-4.}$^[10]

$\xi {\displaystyle }$ ${\displaystyle \xi}$의 정확한 형태는 다음과 같이 표현할 수 있다$$.

${\displaystyle \xi ={\frac{1}{6}{6}}{{17+{\sqrt[{3}}}}}{{249-28848i}}}{\sqrt[{3}}}}}}}}}}{149+28848i{237}}}}}}}}}}}}}}}}}}}}}}}}}}}$

${\displaystyle \xi ={\frac{1}{6}{{\sqrt{6}}}{17+2}{\sqrt{6049}}}}}\cos \left\frac {1}{3}\1}\tan ^{28848}{\sqrt{239}}}}}}}}}오른쪽)}}}}}}}}}}}},}},},},},},},},},},},},},},},},$

여기서 $i{\displaystyle }$ ${\displaystyle i}$은(는) 가상 단위다.

관련 다면체

스너브 디스페노이드의 또 다른 구조는 디지온 자이로비안티코폴라다.위상과 대칭은 같지만 정삼각형은 없다.중심 평면의 사각형에는 회전 대칭이 부착된 두 개의 반추폴레로 4개의 정점이 있다.듀얼은 직각 펜타곤으로 공간을 셀프 셀링할 수 있다.

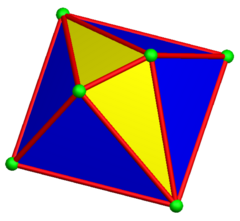디지온항시콜라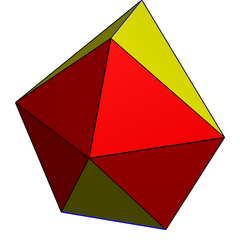

디지온 교량형 부폴라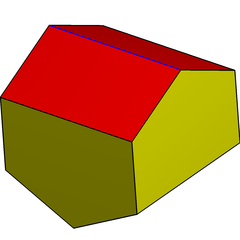

(이중) 길쭉한 교비파스티기움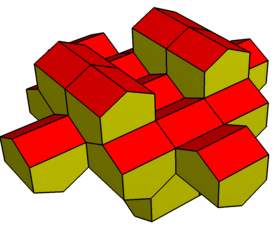

부분 다듬기

참조

외부 링크

• Weisstein, Eric W. "Snub disphenoid". MathWorld.