잘 덮인 그래프

Well-covered graph
잘 덮인 그래프, 육각형의 9개의 대각선을 교차 그래프로 나타낸 것이다.세 개의 빨간 정점은 그것의 14개의 동일한 크기의 최대 독립 세트들 중 하나를 형성하고, 여섯 개의 파란 정점은 보완적인 최소 정점 커버를 형성한다.

그래프 이론에서 잘 덮인 그래프는 모든 최소 꼭지점 커버가 다른 최소 꼭지점 커버와 동일한 크기를 갖는 방향성이 없는 그래프다.동등하게, 이것들은 모든 최대 독립 집합의 크기가 같은 그래프들이다.잘 덮인 그래프는 마이클 D에 의해 정의되고 처음으로 연구되었다. 1970년 배관공

잘 가려진 그래프에는 모든 완전한 그래프, 균형 잡힌 완전한 초당적 그래프, 정점이 체스판의 사각형과 가장자리가 체스 루크의 움직임을 나타내는 룩의 그래프가 포함된다.잘 덮인 입방체 그래프, 잘 덮인 발톱 없는 그래프, 잘 덮인 둘레 그래프의 알려진 특성화는 다항식 시간에 이러한 그래프를 인식할 수 있게 하지만 다른 종류의 그래프가 잘 덮혀 있는지 여부를 테스트하는 것은 coNP-완전한 문제다.

정의들

그래프의 꼭지점 표지는 그래프의 모든 가장자리에 닿는 정점 집합이다.정점 커버는 최소 또는 중복되지 않으며, 정점을 제거하면 커버 속성을 파괴할 수 있다.정점이 적은 다른 꼭지점 커버가 없는 경우 최소값이다.잘 덮인 그래프는 모든 최소 커버도 최소인 그래프다.잘 덮인 그래프를 정의한 원본 논문에서 플럼머는 최소 커버 두 개마다 서로 동일한 수의 정점을 갖는 속성과 "분명히 동등하다"고 쓰고 있다.[1]

그래프의 독립 집합은 두 개 중 어느 것도 서로 인접하지 않는 정점 집합이다.C가 그래프 G의 꼭지점 표지인 경우, C의 보완점은 독립 집합이어야 하며, 그 반대의 경우도 마찬가지여야 한다.C는 그것의 보완물 I가 최대 독립 세트인 경우에만 최소 정점 커버이고, C는 그것의 보완물이 최대 독립 세트인 경우에만 최소 정점 커버다.따라서 잘 덮인 그래프는 동등하게 모든 최대 독립 집합이 동일한 크기를 갖는 그래프 또는 최대 독립 집합이 최대인 그래프를 의미한다.[2]

잘 덮인 그래프를 정의한 원본 논문에서 이러한 정의는 연결이 끊긴 그래프에도 의미가 있지만 연결된 그래프로 제한되었다.[3]일부 후기 저자는 잘 덮인 그래프가 어떤 고립된 정점을 가지지 않아야 한다는 더 약한 요구조건으로 연결 요건을 대체했다.[4]잘 가려진 그래프와 분리된 정점이 없는 잘 가려진 그래프 둘 다에 대해, 모든 최소 정점 커버에 속하는 필수 정점, 정점이 있을 수 없다.[3]또한 잘 가려진 모든 그래프는 모든 정점 v에 대해 그래프에서 v를 삭제하면 최소 정점 커버가 더 작은 그래프가 생성된다는 점에서 정점 커버에 대한 중요한 그래프다.[3]

그래프 G의 독립성 콤플렉스는 G의 각 독립성 세트마다 심플렉스(simplex)를 갖는 단순화 콤플렉스다. 단순화 콤플렉스의 모든 최대 단순화가 동일한 카디널리티를 갖는다면, 잘 덮인 그래프는 순수 독립성 콤플렉스를 가진 그래프와 동등하게 동일하다고 한다.[5]

예

abcdefgh
8
Chessboard480.svg
d8 white rook
g7 white rook
c6 white rook
a5 white rook
b4 white rook
h3 white rook
e2 white rook
f1 white rook
8
77
66
55
44
33
22
11
abcdefgh
체스 보드에 8명의 루크를 공격하지 않는 배치.체스보드에 8명 미만의 루크를 비공격 방식으로 배치하면 비공격으로 남아 있는 루크 8명까지 늘일 수 있다.

길이 4, 5의 사이클 그래프는 잘 가려져 있다: 각각의 경우, 모든 최대 독립 집합은 크기가 2이다.길이 7의 주기, 길이 3의 길도 잘 가려져 있다.모든 완전한 그래프는 잘 가려져 있다. 모든 최대 독립 집합은 하나의 꼭지점으로 구성된다.마찬가지로 모든 군집 그래프(완전한 그래프의 분리된 결합)는 잘 가려져 있다.완전한 양분 그래프는 양분 간의 정점 수가 같을 경우 잘 다루어지는데, 이는 두 개의 최대 독립 집합에 불과하기 때문이다.루크의 그래프는 잘 다루어져 있다: 만약 어떤 루크를 체스판 위에 놓아 두 명의 루크가 서로 공격하지 않도록 한다면, 체스판의 모든 행과 열에 하나씩 있을 때까지 계속해서 더 많은 비공격 루크를 배치할 수 있다.

P가 다각형 또는 점 집합인 경우, S는 P의 정점을 끝점으로 가지고 있고 그렇지 않으면 P와 분리되는 개방형 선 세그먼트의 집합이며, G는 S의 교차 그래프(S의 각 선 세그먼트에 정점을 갖는 그래프와 서로 교차하는 각 두 선 세그먼트에 대한 가장자리를 갖는 그래프)인 경우 G는 잘 가려진다.이 경우 G에 설정된 모든 최대 독립성은 P의 삼각측량에서 가장자리 집합에 해당하며, 오일러 특성을 포함한 계산은 두 삼각측량마다 가장자리 수가 서로 동일하다는 것을 보여준다.[6]

만약 G가 n-vertex 그래프라면, 1-edge 그래프(즉, G에 각각 1도씩, 그리고 G의 뚜렷한 꼭지점에 인접한 G에 n개의 새로운 정점을 추가함으로써 형성된 그래프 H)를 가진 G의 뿌리가 잘 가려진다.단, H에 있는 최대 독립 집합은 G에 있는 임의의 독립 집합과 보완 집합의 도 1 이웃으로 구성되어야 하며, 따라서 n 크기를 가져야 한다.[7]보다 일반적으로, 어떤 그래프 G와 클릭 커버(G의 정점을 clique로 분할 p)를 함께 보면, 각 클릭에 다른 정점을 추가함으로써 형성된 그래프 G는p 잘 가려진다. p가 n개의 단일 Vertex click으로 구성되었을 때 뿌리가 있는 제품은 이 구조의 특별한 경우다.[8]따라서 모든 그래프는 잘 덮인 그래프의 유도 하위그래프다.

초당성, 매우 잘 적용된 그래프 및 둘레

Favaron(1982)은 매우 잘 덮인 그래프를 각 최대 독립 세트(따라서 각 최소 꼭지점 커버도 포함)가 정점의 정확히 절반을 포함하는 잘 덮인 그래프라고 정의한다.이 정의는 그래프 G와 단일 에지 그래프의 루트 제품을 포함한다.예를 들어, 라빈드라(1977년)와 베르게(1981년)가 연구한 초당적 잘 덮인 그래프를 포함한다. 정점이 분리되지 않은 초당적 그래프에서, 어떤 양분적 독립 집합(그리고 최소 정점 커버)의 양면 모두 최대 정점이므로, 그래프가 잘 덮인 경우 양쪽의 정점이 똑같이 많아야 한다.정점이 없는 잘 덮인 그래프에서 최대 독립 집합의 크기는 최대 n/2이므로 잘 덮인 그래프는 최대 독립 집합 크기가 가능한 한 큰 잘 덮인 그래프입니다.[9]

초당적 그래프 G는 M의 모든 에지 UV에 대해 u와 v의 유도 하위 그래프가 완전한 초당적 그래프를 형성하는 속성과 완벽하게 일치하는 M을 가진 경우에만 잘 탐지된다.[10]일치에 대한 특성화는 초당적 그래프에서 매우 잘 적용된 그래프까지 확장될 수 있다. 그래프 G는 다음 두 가지 속성과 완벽하게 일치하는 M을 가진 경우에만 매우 잘 다루어진다.

  1. M의 어떤 가장자리도 G의 삼각형에 속하지 않으며,
  2. M의 가장자리가 G에서 3 에지 경로의 중심 가장자리인 경우 경로의 두 끝점이 인접해야 한다.

더욱이 G가 매우 잘 가려진다면 G의 모든 완벽한 매칭은 이러한 성질을 만족시킨다.[11]

나무는 초당적 그래프의 특별한 경우로서, 나무가 잘 가려져 있는지를 시험하는 것은 잘 가려진 초당적 그래프의 특성화에 대한 훨씬 단순한 특수한 경우로서 취급할 수 있다: G가 정점이 두 개 이상인 나무라면, 나무의 각 잎이 아닌 노드가 정확히 한 잎에 인접한 경우에만 잘 가려진다.[10]동일한 특성화는 모든 꼭지점의 지름이 낮은 이웃이 반복적이라는 점에서 국소적으로 나무와 유사한 그래프에 적용된다. 즉, 그래프가 8번째 이상(모든 꼭지점 v에 대해 모든 꼭지점 3의 거리 내 정점 하위 그래프가 반복됨)인 경우, 모든 꼭지점이 다음보다 큰 경우에만 잘 탐지된다.1급 이웃이 딱 한 명 있다.[12]밀접하지만 더 복잡한 특성화는 잘 가려진 5번째 그래프에 적용된다.[13]

규칙성 및 평면성

7입방 세 개로 연결된 잘 덮인 그래프
6노드 경로의 각 노드를 3개의 조각 중 1개로 교체하여 형성된 1입방체 연결 잘 덮인 그래프
스너브 디스페노이드(snub disphenoid)는 잘 덮인 4개의 4차원 연결 3차원 단순 다면체 중 하나이다.

잘 덮인 입방(3-정규) 그래프는 7개의 3 연결 예제와 3개의 연결성이 낮은 입방 그래프 무한 제품군으로 구성된다.[14]

3개 연결된 입방체 잘 덮인 7개의 그래프는 완전한 그래프 K4, 삼각 프리즘과 오각형 프리즘의 그래프, 뒤러 그래프, 효용 그래프3,3 K, Y-Δ 변환에 의해 효용 그래프에서 얻은 8Vertex 그래프, 그리고 14Vertex 일반화된 피터슨 그래프 G(7,2)이다.[15]이 그래프들 중 첫 번째 네 개는 평면 그래프다.그것들은 잘 가려진 유일한 4입방 다면 그래프(단순 볼록 다면체의 그래프)이다.그래프 중 4개(두 프리즘, 뒤러 그래프, G(7,2)는 일반화된 피터슨 그래프다.

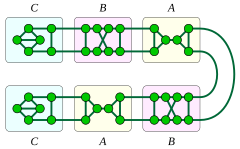
1번과 2번 연결된 입방체 잘 덮인 그래프는 모두 경로나 사이클의 노드를 플럼머(1993)가 A, B, C로 표기하는 3개의 그래프 조각으로 대체함으로써 형성된다.단편 A 또는 B는 사이클의 노드나 경로의 내부 노드를 대체하는 데 사용될 수 있으며, 조각 C는 경로의 두 엔드 노드를 대체하는 데 사용될 수 있다.파편 A에는 브리지가 포함되어 있으므로 경로에 이 교체 프로세스를 수행하고 파편 A를 사용하여 경로 노드 일부(및 나머지 노드에 대한 나머지 2개 파편)를 교체한 결과는 1Vertex로 연결된 입방체 잘 덮인 그래프가 된다.모든 1-Vertex 연결 입방체 잘 덮인 그래프는 이러한 형태를 가지고 있으며, 그러한 모든 그래프는 평면형이다.[14]

2-Vertex 연결 입방체 잘 덮인 그래프는 두 종류가 있다.이 두 패밀리 중 하나는 사이클의 노드를 조각 A와 B로 교체하여 형성되는데, 조각 중 적어도 두 개 이상이 A 유형이다. 이 유형의 그래프는 B 유형의 파편이 포함되지 않은 경우에만 평면이다.다른 패밀리는 경로의 노드를 유형 B와 C의 조각으로 대체하여 형성된다. 이러한 모든 그래프는 평면이다.[14]

잘 덮인 단순 다면체의 특성화를 3차원으로 보완하면서, 연구자들은 잘 덮인 단순 다면체 또는 동등하게 잘 덮인 최대 평면 그래프를 고려했다.정점이 5개 이상인 모든 최대 평면 그래프는 정점 연결 3, 4, 5가 있다.[16]잘 가려진 5개의 최대 평면 그래프는 없으며, 4개의 잘 연결된 최대 평면 그래프, 즉 정규 팔면체 그래프, 오각형 디피라미드, 스너브 디스페노이드, 정점 12개, 모서리 30개, 삼각면 20개를 가진 불규칙 다면체(비콘벡스 델타헤드론)만 있을 뿐이다.그러나, 3개의 연결이 잘 된 잘 덮인 최대 평면 그래프가 무한히 많다.[17]예를 들어, 잘 덮인 3-연결된 최대 평면 그래프는 각각의 면에 새로운 정점을 추가하여 분리 삼각형 면이 있는 3-Vertex 최대 평면 그래프를 통해 클릭 커버 구조를[8] 통해 얻을 수 있다.

복잡성

그래프에 크기가 다른 두 개의 최대 독립 집합이 포함되어 있는지 여부를 테스트하는 것은 NP-완전하다. 즉, 보완적으로 그래프를 잘 덮었는지 테스트하는 것은 coNP-완전하다.[18]잘 탐지된 것으로 알려진 그래프에서 최대 독립 세트를 쉽게 찾을 수 있지만, 알고리즘이 출력물로 생성하는 것도 모든 그래프에서 최대 독립 집합이나 입력이 잘 탐지되지 않는다는 보장이 NP-hard이다.[19]

이와는 대조적으로, 주어진 그래프 G가 다항식 시간에 매우 잘 포함되는지 여부를 검정할 수 있다.그렇게 하려면 매우 잘 덮인 그래프에서 일치된 에지의 두 가지 특성을 만족시키는 가장자리로 구성된 G의 하위 그래프 H를 찾은 다음 일치 알고리즘을 사용하여 H가 완벽한 일치를 가지고 있는지 테스트한다.[11]해밀턴 사이클을 찾는 문제와 같이 임의 그래프에 대해 NP-완전한 일부 문제는 매우 잘 적용된 그래프의 경우 다항 시간 내에 해결될 수도 있다.[20]

그래프는 모든 최대 일치가 최대일 경우 등치할 수 있으며, 즉 선 그래프가 잘 가려져 있으면 등치할 수 있다고 한다.선 그래프, 또는 더 일반적으로 발톱이 없는 그래프가 다항식 시간에 잘 가려져 있는지 여부를 테스트할 수 있다.[21]

잘 덮인 그래프와 잘 덮인 그래프가 5번째 이상이고 3번째 정규 그래프를 잘 덮은 그래프의 특성화는 이러한 그래프를 인식하는 효율적인 다항식 시간 알고리즘으로 이어진다.[22]

메모들

  1. ^ 배관공(1970년).
  2. ^ 배관공(1993년).
  3. ^ a b c 배관공(1970년).
  4. ^ 파바론(1982년).
  5. ^ 이 용어를 사용하는 논문의 예는 Dochtermann & Engström(2009) 및 Cook & Nagel(2010)을 참조하십시오.
  6. ^ 그린버그(1993년).
  7. ^ 이 예제의 등급은 Fink 등(1985)에 의해 연구되었다; 그것들은 또한 (또한 잘 가려진 네 개의 에지 사이클과 함께) 정확히 지배 번호가 n/2인 그래프들이다.잘 가려지는 특성도 도흐터만&엥스트룀(2009)의 정리 4.4로 다른 용어(순수한 독립 콤플렉스를 가지고 있음)로 명시되어 있다.
  8. ^ a b 쿡 앤 나겔(2010년).
  9. ^ 버지(1981년).
  10. ^ a b 라빈드라(1977년), 플럼머(1993년).
  11. ^ a b 스테이플스(1975년), 파바론(1982년), 플럼머(1993년).
  12. ^ 핀보우&하트넬(1983); 플러머(1993) 정리 4.1.
  13. ^ Finbow & Hartnell (1983년), Flummer (1993년), Organis 4.2.
  14. ^ a b c 캠벨(1987년), 캠벨 & 플럼머(1988년), 플럼머(1993년).
  15. ^ 캠벨(1987년), 핀보우, 하트넬 & 노워크스키(1988년), 캠벨, 엘링엄 & 로일(1993년), 플럼머(1993년).
  16. ^ 1, 2, 3, 4 정점에 대한 전체 그래프는 모두 최대 평면이며 잘 가려져 있다. 정점 연결은 큰 최대 평면 그래프와 무관한 정점 연결 정의의 세부사항에 따라 제한되지 않거나 최대 3개까지이다.
  17. ^ 핀보우, 하트넬, 노와코프스키 외 연구진.(2003, 2009, 2010).
  18. ^ Sankaranayana & Stewart(1992);체바탈&슬레이터(1993); 카로, 세브&타르시(1996).
  19. ^ 라그하반 & 스핀래드(2003년).
  20. ^ Sankaranayana & Stewart(1992년).
  21. ^ 레스크, 플럼머 & 풀리블랭크(1984); 탱커스 & 타르시(1996);Tankus & Tarsi(1997년).
  22. ^ 캠벨, 엘링햄 & 로일(1993); 플럼머(1993).

참조