축전행

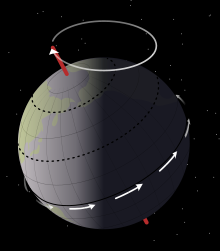
천문학에서 축전행은 중력에 의해 유도되고 느리며 천문체의 회전축 방향의 연속적인 변화다. 특히 약 26,000년의 주기로 지구의 자전축 방향의 점진적인 변화를 가리킬 수 있다.^[1] 이것은 축이 그들의 유인원에서 결합한 한 쌍의 원뿔을 추적하여 회전하는 팽이의 전열과 비슷하다. "정착"이라는 용어는 일반적으로 운동에서 이 가장 큰 부분만을 가리킨다; 지구 축의 정렬에서 다른 변화들 -영양과 극운동 -은 크기가 훨씬 작다.

지구의 전열은 역사적으로 미분분의 전열이라고 불렸는데, 미분류는 고정된 별에 상대적인 황색계를 따라 서쪽으로 이동했기 때문이며, 황색계를 따라 태양의 연간 운동과는 정반대였다. 역사적으로 ^[2]분수의 전과를 발견한 것은 대개 서양에서 2세기 BC 천문학자 히파르쿠스의 소행으로 여겨진다. 19세기 전반기의 행성들 사이의 중력 계산 능력이 향상되면서, 1863년경부터 황반자체가 약간 움직인 것을 인정받았는데, 이 황반자체는 행성의 전처리라고 이름 붙여진 반면, 지배적인 성분은 황반자 전처리라고 이름 붙여졌다.^[3] 그들의 조합은 춘분(春分)의 전분(前分) 대신 일반적 전분(前分)으로 명명되었다.

루니솔라 전열은 지구 적도 불룩에 있는 달과 태양의 중력에 의해 발생하며, 관성 공간에 관해서 지구의 축이 움직이게 한다. 행성의 전열(진각)은 지구상의 다른 행성의 중력과 그 궤도면(황반) 사이의 작은 각도로 인해 황반면의 평면이 관성 공간에 비해 약간 이동하게 된다. 루니솔라 전극은 행성 전극보다 약 500배 크다.^[4] 달과 태양 외에 다른 행성들도 관성 공간에서 지구 축의 작은 움직임을 일으켜 루니솔라 대 행성이라는 용어의 대조를 오도하기 때문에 2006년 국제천문연맹은 지배적인 성분의 이름을 적도의 전열로 바꾸고, 부성분의 이름을 바꿀 것을 권고했다.황혈의 전치(前治)는 dp percession, but the composition은 여전히 일반적 전치(前治)라고 명명된다.^[5] 옛 용어에 대한 많은 언급이 그 변화 이전의 출판물에 존재한다.

명명법

"precession"과 "procession"은 모두 운동에 관련된 용어다. "precession"은 라틴어 praecedere("앞서, 앞 또는 앞쪽으로")에서 파생된 반면, "procession"은 라틴어 praecedere("진행, 앞으로 나아가기")에서 파생된 것이다. 일반적으로 "프로세션"이라는 용어는 앞으로 나아가는 물체의 그룹을 설명하기 위해 사용된다. 지구에서 바라본 별들은 지구의 주간 운동으로 인해, 그리고 태양을 중심으로 한 지구의 회전으로 인해, 매일 동쪽에서 서쪽으로 이동하는 것으로 보인다. 동시에 별들은 그러한 움직임을 약간 예상하는 것을 관찰할 수 있는데, 연간 약 50 아크 초의 비율로, "분분의 예"라고 알려진 현상이다.

이 운동을 기술하면서 천문학자들은 일반적으로 용어들을 단순히 "precession"으로 줄였다. 운동 물리학자들의 원인에 대해서도 설명하면서, 관측할 수 있는 현상과 그 원인에 대해 어느 정도 혼동을 가져왔는데, 천문학에서는 어떤 전이가 진짜고 다른 것은 명백하기 때문에 중요한 것이다. 이 문제는 많은 천문학자들이 물리학자나 천체물리학자라는 사실에 더욱 난독하게 된다.

천문학에서 사용되는 '정진'이라는 용어는 일반적으로 분분(하늘을 가로질러 역행하는 별)의 관측 가능한 전진을 기술하는 반면, 물리학에 사용되는 '정진'이라는 용어는 일반적으로 기계적인 과정을 기술한다.

영향들

지구 축의 전열은 여러 가지 관측 가능한 효과를 가지고 있다. 첫째로, 남극과 북극의 천체들의 위치는 우주 고정된 별들의 배경과 반대로 원을 그리며 움직이는 것으로 나타나 약 26,000년 만에 하나의 회로를 완성한다. 따라서 오늘날 폴라리스 항성이 대략 북극 천체에 놓여 있는 반면, 이것은 시간이 지남에 따라 변할 것이고, 다른 별들은 "북극성"이 될 것이다.^[2] 약 3,200년 후, 세페우스 별자리에 있는 별 감마 세페이는 폴라리스의 뒤를 이어 이 자리에 오를 것이다. 남극은 현재 위치를 표시할 수 있는 밝은 별이 부족하지만, 시간이 흐를수록 밝은 별들이 남쪽 별이 되는 원인이 되기도 한다. 천극이 이동함에 따라 지구상의 특정 위치에서 볼 때 전체 항성장의 외관상 방향에는 그에 상응하는 점진적인 변화가 있다.

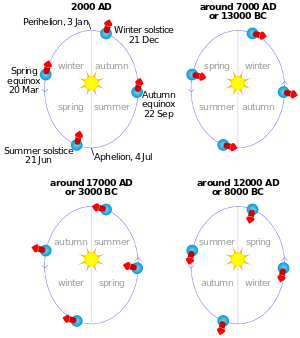
둘째로, 태양 주위의 궤도에 있는 지구의 위치는 계절에 따라 정의된 용광로, 분점 또는 다른 시간에서 천천히 변화한다.^[2] 예를 들어, 지구의 축 기울기가 태양을 바로 향할 때 지구의 궤도 위치가 하지에 표시되어 있다고 가정해 보자. 하나의 완전한 궤도 후에, 태양이 배경별에 상대적으로 외관상 같은 위치로 돌아왔을 때, 지구의 축방향 기울기는 현재 태양을 향해 직접적으로 있지 않다: 전정작용의 효과 때문에, 이것은 약간 "이상의" 방법이다. 즉, 동지는 궤도에서 조금 일찍 발생했다는 것이다. 따라서 계절의 순환을 측정하는 열대년(예를 들어, 동지부터 동지까지의 시간, 또는 이분에서 이분까지의 시간)은 항성에 대한 태양의 겉보기 위치에 의해 측정되는 측연보다 약 20분 정도 짧다. 약 26,000년 후 그 차이는 1년에 달하므로, 궤도에 상대적인 계절의 위치는 "시작했던 곳으로" 돌아온다.(기타 효과 또한 지구의 궤도의 모양과 방향을 서서히 변화시키고, 이것들은 전열과 결합하여 서로 다른 기간의 다양한 사이클을 만들어낸다; 밀란코비치 사이클도 참조한다. 지구의 기울기의 규모도 단순히 방향과 반대로 시간이 지남에 따라 서서히 변화하지만, 이러한 영향은 직접 과도현상에 기인하지는 않는다.)

동일한 이유로, 계절에 따라 정해진 시간에 별의 배경에 상대적인 태양의 겉보기 위치는 12개의 전통적인 별자리를 통해 360°의 전체 방향을 천천히 역행하며, 연간 약 50.3초, 또는 71.6년마다 1도의 비율로 한다.

현재에 있어서, 경과율은 2만5772년의 기간에 해당하지만, 그 비율 자체는 시간에 따라 다소 차이가 있으므로(아래 값 참조), 정확히 2만5772년 내에 지구의 축이 현재의 위치로 되돌아간다고는 말할 수 없다.

자세한 내용은 아래의 극 별 변경 및 극지 이동 및 분점 이동을 참조하십시오.

역사

헬레니즘 세계

히파르쿠스

전치사의 발견은 보통 로도스나 그리스의 천문학자 니케아의 히파르쿠스(190–120 BC)에 기인한다. 프톨레마이오스의 알마게스트에 따르면 히파르쿠스는 스피카와 다른 밝은 별들의 경도를 측정했다. 그는 자신의 치수를 전임자인 티모차리스(기원전 320–260년)와 아리스틸러스(기원전 약 280년)의 데이터와 비교하면서 스피카가 추분에 비해 2° 움직였다고 결론지었다. 그는 또 열대년(태양이 분산으로 돌아오는 데 걸리는 시간)과 부성년(태양이 고정된 항성으로 돌아오는 데 걸리는 시간)의 길이를 비교한 결과 약간의 차이가 있음을 발견했다. 히파르쿠스는 분수가 십이지장을 통해 이동("전처리")하고 있다고 결론지었고, 다시 말해 1세기에는 전처리 속도가 1도 이상, 즉 36000년 이내에 완전한 사이클을 완성했다고 한다.^[6]

사실상 히파르쿠스의 모든 글들이 사라졌는데, 그 중에는 그의 전처리 작업도 포함되어 있다. 그것들은 프톨레마이오스가 언급하는데, 프톨레마이오스는 움직이지 않는 지구 주위를 도는 천체의 회전이라고 설명한다. 프톨레마이오스와 마찬가지로 히파르쿠스도 지구보다는 지반적 용어의 전과를 하늘의 운동으로 생각했다고 보는 것이 타당하다.

프톨레마이오스

히파르쿠스의 전처리 작업을 계속한 것으로 알려진 최초의 천문학자는 서기 2세기 프톨레마이오스다. 프톨레마이오스는 일식이 필요 없는 히파르쿠스의 달 방법의 변형으로 레굴루스, 스피카 등 밝은 별들의 위도를 측정했다. 해가 지기 전에 그는 달과 태양을 구분하는 세로 호를 쟀다. 그리고 해가 진 후 달에서 별까지의 호를 재었다. 그는 태양의 경도를 계산하기 위해 히파르쿠스의 모형을 사용했고, 달의 움직임과 시차(Evans 1998, 페이지 251–255)에 대한 수정을 했다. 프톨레마이오스는 자신의 관측을 히파르쿠스, 알렉산드리아의 메넬라오스, 티모차리스, 아그리파가 만든 관측과 비교했다. 그는 히파르쿠스 시대와 자기 시대(약 265년) 사이에 별들이 100년 만에 2°40' 또는 1°(연간 36"), 오늘날 받아들여지는 비율은 연간 약 50" 또는 72년 만에 1°라는 것을 발견했다. 그러나 프톨레마이오스가 스스로 치수를 재는 대신 히파르쿠스의 몸매를 단순히 신뢰했을 가능성도 있다. 그는 또한 과열이 황반 근처의 항성뿐만 아니라 모든 고정된 항성에도 영향을 미친다는 것을 확인했으며, 그의 주기는 히파르쿠스가 발견한 것과 같은 3만 6천 년의 기간을 가졌다.^[6]

기타저작

대부분의 고대 작가들은 전과를 언급하지 않았고, 아마도, 그것에 대해 알지 못했을 것이다. 예를 들어 프롤러스는 사전 처리를 거부했고, 4세기 프톨레마이오스 해설자인 알렉산드리아의 테온은 프톨레마이오스의 설명을 받아들였다. 테온은 또한 다음과 같은 대체 이론을 보고한다.

어떤 견해에 따르면 고대 점성술사들은 어떤 시대부터 용해성 기호는 기호의 순서에 따라 8°의 운동을 하고 그 후에는 같은 양을 거슬러 올라간다고 믿는다.(Dreyer 1958, 페이지 204).

12궁도의 전체 순서를 진행하는 대신, 8°의 호를 두고 등락으로 "철근"한다. Teon은 삼분오열설을 대안으로 제시한다.

대체발견 이론

바빌로니아인

다른 문화권에서는 히파르쿠스와는 독립적으로 분열을 발견했다는 다양한 주장이 제기되어 왔다. 알 바타니에 따르면, 찰데인 천문학자들은 약 기원전 330년까지, 부정확하다면, 전과를 설명할 수 있는 위치에 놓일 수 있도록, 열대성과 반실제 연도를 구분하였지만, 그러한 주장은 일반적으로 지지할 수 없는 것으로 간주된다.^[7]

마야

고고학자 수잔 밀브래스는 "플레이아데스인들이 참여한 3만 년의 메소아메리카 롱카운트 달력이 분천의 전과를 계산하기 위한 노력이었을 것"^[8]이라고 추측했다. 이 견해는 마야 문명의 다른 전문 학자들이 거의 갖고 있지 않다.^{[citation needed]}

고대 이집트인

히파르쿠스 시대(Ptolemaic 시대) 이전인 왕조 시대에 고대 이집트에서도 전이가 알려졌다는 비슷한 주장이 제기돼 왔다. 그러나 이러한 주장은 여전히 논란이 되고 있다. 예를 들어 카르낙 신전 단지의 일부 건물들은 일 년 중 중요한 시기에 특정 별이 뜨거나 지는 지평선 지점을 지향했다고 한다.^{[citation needed]} 그럼에도 불구하고, 그들은 정확한 달력을 유지했고 사찰 재건 날짜를 기록한다면 대략적인 진행률을 계획하는 것은 꽤 간단한 문제가 될 것이다. 덴데라 조디악은 늦은(Ptolemaic) 시대부터 덴데라에 있는 하토르 사원의 별 지도로, 분수의 전과를 기록한 것으로 알려져 있다(Tompkins 1971) 어쨌든 고대 이집트인들이 전과를 알았다면, 그들의 지식은 살아남은 어떤 천문학적 문헌에도 그렇게 기록되지 않는다.

마이클 라이스는 자신의 이집트 유산에 "기생인들이 기원전 2세기 비티니아인 히파르코스가 정의하기 전에 프리세션의 역학을 알았는지 여부는 불확실하지만 밤하늘에 대한 헌신적인 관찰자로서 그 영향을 알아채지 못할 수는 없다."(p 128) 라이스는 "프리세션은 근본적인 것"이라고 믿고 있다. 이집트의 발전에 원동력이 된 것을 이해한다."(10페이지)는 "어떤 의미에서 민족 국가로서의 이집트와 살아있는 신으로서의 이집트 왕은 이집트인들이 말하는 천문학적 변화의 실현의 산물"(56페이지)이다. 라이스 장관은 "기자의 피라미드가 별과의 정렬에 의해서만 달성될 수 있었던 정밀도에서 가장 정제된 천문관측이 기원전 3천년에 이집트에서 실행되었다는 증거는 (아마도 그 이전에도) 기자의 피라미드가 기준점에 맞춰져 있다는 점에서 명백하다"고 말했다. " (p. 31) 이집트인들은 또한 "신왕국 시대에 여러 번 일어난 것으로 보이는, 원래 위치가 정해진 별의 위치가 사전 처리의 결과로 그 위치를 이동했을 때 성전의 방향을 바꾸려고 했다." (p. 170)

인도

1200년 이전에 인도는 두 가지 공포증 이론이 있었는데 하나는 비율이고 다른 하나는 비율 없는 이론이었고, 몇 가지 관련 모델들이 있었다. 각자는 여러 해설자들에 의해 사소한 변화나 수정을 받았다. 이 세 가지 중 가장 존경 받는 인도의 천문학자 Surya Siddhanta (3:9–12)가 묘사한 공포감이 지배적인데, 400으로 구성되었으나 다음 몇 세기 동안 수정되었다. 그것은 상담한 그룹에 따라 황경 19°11°~23°51°에 걸쳐 변화하면서 여전히 모든 인도 달력에 사용되는 사이드리얼 에볼루션(sidereal epoech, abanamsa)을 사용했다.^[9] 이 시대는 대략 30년 정도의 인도의 달력을 현대 춘분 23-28일 후에 시작하게 한다. 수리아 싯단타의 춘분은 사이드리얼 시대부터 양방향으로 27°의 장서를 장식했다. 따라서 분분은 한 방향으로 54° 이동했고, 다른 방향으로 54° 후퇴했다. 이 사이클을 완료하는 데 연 54″의 비율로 7200년이 걸렸다. 이분은 -3101년 칼리 유가의 시초에서 시대와 일치했고, 499년 3600년 후에 다시 한 번 시대와 일치했다. 최대 편차가 27°에 달했을 때 -1301로 이 해 사이에 프로그램 중심에서 역행으로 바뀌었고, 2299년까지 3600년 동안 현대의 전행과 같은 방향인 역행으로 남아 있었을 것이다.^{[10][11]: 29–30}

또 다른 공포증은 바라하미히라(550)c.에 의해 설명되었다. 그의 공포는 한 방향으로 46°40°의 호와 출발점으로 되돌아가는 것으로 구성되었다. 이 호 23°20°의 절반은 해협에서 적도 양쪽에 있는 태양의 최대 열화와 동일했다. 그러나 기간이 명시되지 않았기 때문에 연간 비율을 확인할 수 없다.^{[11]: 27–28}

몇몇 저자들은 4억 3천만 년의 칼파에서 20만 회전에 가까운 회전이 일어났다고 설명했는데, 이는 그 비율이 될 것이다. 200,000×360×3600/4,320,000,000 = 60″/년 그들은 아마도 누적된 전과를 거의 500번 가까이 0으로 만들기 위해 20만번 회전에서 벗어났을 것이다. 비스누칸드라 c.(550–600)는 칼파 또는 56.8//년의 18만9411개의 혁명을 언급하고 있다. 바스카라 1세(c.600–680)는 칼파 또는 58년의 [1]94,110개의 혁명을 언급하고 있다.1년 2개월. 바르샤라 2세(c.1150년)는 칼파 또는 59년의 19만9699번 혁명을 언급하고 있다.9시 15분/^{[11]: 32–33} 년

중국 천문학

유시(劉時, AD 4세기)는 중국 천문학자 중 최초로 전과를 언급했다. 그는 50년 후 경과율을 1°로 추정했다(Pannekoek 1961, 페이지 92).

중세시대와 르네상스

중세 이슬람 천문학에서는 프톨레마이오스의 알마게스트에 근거하여, 그리고 그 가치를 정제하는 관찰에 의해 전이가 알려져 있었다.

알 바타니는 '지 알 사비'에서 히파르쿠스 계산법과 프톨레마이오스의 100년 당 1도 값을 언급한 후, 그가 전과를 측정한 결과 66년 당 1도임을 발견했다고 말한다.^[12]

이후 알 수피 교수는 자신의 <고정성서>에서 프톨레마이오스의 전처리 가치가 100년 태양년 당 1도라고 언급하고 있다. 이어 알마문 집권기에 행해진 지 알 뭄타한과는 다른 가치를 66년 태양년에 1도씩 인용한다. 그는 또한 앞에서 언급한 알 바타니의 '지 알 사비'를 알 바타니의 시간과 프톨레마이오스의 시간 차이를 설명하기 위해 항성의 좌표를 11도 10분씩 조정한 것으로 인용한다.^[13]

이후 마라게 천문대에서 편찬한 지제이 일카니는 분수의 전과를 연 51 아크초로 설정하는데, 이는 현대적 가치인 50.2 아크초에 매우 가깝다.^[14]

중세 이슬람과 라틴 기독교 천문학자들은 "trepidation"을 고정된 별들의 움직임으로 취급했다. 이 이론은 일반적으로 아랍 천문학자 타비트 ibn 쿠라에게 귀속되지만, 현대에 와서 귀속은 논쟁되어 왔다. 니콜라우스 코페르니쿠스는 디 레볼루션 오르비움 코엘레스티움(1543년)에 다른 공포증 설명을 발표했다. 이 작품은 지구 축의 움직임의 결과로서 첫 번째로 지구 전열에 대한 확실한 언급을 한다. 코페르니쿠스는 지구의 세 번째 움직임으로 전과를 특징지었다.^[15]

근대

1세기 이상 지난 후에 아이작 뉴턴의 <철학>(1687)에서 중력의 결과라고 설명되었다(Evans 1998, 페이지 246). 그러나 뉴턴의 원래 전처리 방정식은 효과가 없었고, 장 르 론드 달랑베르트와 그 이후의 과학자들에 의해 상당히 수정되었다.

히파르쿠스의 발견

히파르쿠스는 '솔스트론적 및 등정적 포인트의 변위에 대하여'(알마제스트 III.1과 VII.2에 설명)에서 자신의 발견에 대해 설명했다. 그는 월식 때 별 스피카의 황경도를 측정하여 추분에서 서쪽으로 6° 정도 떨어진 것을 알아냈다. 그는 자신의 치수를 알렉산드리아의 티모차리스(기원전 3세기 초 아리스티루스와 함께 일했던 유클리드 동시대 사람)의 치수와 비교함으로써 그 사이에 스피카의 경도가 약 2° 감소했음을 알아냈다(정확한 연도는 알마게스트에서는 언급되지 않는다). 또한 VII.2에서 프톨레마이오스는 스피카를 포함한 두 개의 별에 대해 보다 정밀한 관찰을 제공하며 각 경우 2°로 결론을 내린다.40'의 변화는 기원전 128년과 AD 139년 사이에 일어났다. (헨체, 세기당 1° 또는 36000년 동안의 완전한 사이클, 즉 프톨레마이오스가 보고한 히파르쿠스의 전주기; 토머의 알마게스트 번역의 cf. 328페이지, 1998년판) 그는 다른 별들에서도 이러한 움직임을 알아차렸다. 그는 12궁도 근처의 별들만이 시간이 지남에 따라 이동했다고 추측했다. 프톨레마이오스는 이것을 자신의 "첫 번째 가설"(Amalagest VII.1)이라고 불렀지만, 히파르쿠스가 고안했을지도 모르는 그 이후의 가설은 보고하지 않았다. 히파르쿠스는 그의 추측을 제한한 것이 분명한데, 그것은 별로 믿을 만한 것이 못 되는 몇 개의 오래된 관찰만 가지고 있었기 때문이다.

등점들이 하늘에 표시되어 있지 않기 때문에 히파르쿠스는 달이 기준점으로 필요했다; 그는 월식을 별의 위치를 측정하기 위해 사용했다. 히파르쿠스는 이미 언제라도 태양의 경도를 계산할 수 있는 방법을 개발했다. 월식은 달이 반대편에 있을 때, 정확히 태양으로부터 180° 떨어진 보름달 동안에 일어난다. 히파르쿠스는 스피카와 달을 분리하는 세로 호를 측정했다고 생각된다. 이 값에 그는 계산된 태양의 경도에 달 경도 180°를 더했다. 그는 Timocharis의 데이터로 동일한 절차를 수행했다(Evans 1998, 페이지 251). 이러한 일식과 같은 관찰은 히파르쿠스에 대한 다른 전기적 정보가 미미하기 때문에 우연히 히파르쿠스가 언제 일했는지에 대한 자료의 주요 원천이다. 예를 들어 그가 관찰한 월식은 기원전 146년 4월 21일과 기원전 135년 3월 21일에 일어났다(토머 1984, 페이지 135n. 14).

히파르쿠스는 또한 On the Length of the Year에서 전과를 공부했다. 두 종류의 해는 그의 작품을 이해하는 것과 관련이 있다. 열대년은 지구에서 바라본 태양이 황색(천구의 항성들 사이의 경로)을 따라 같은 위치로 돌아가기 위해 걸리는 시간이다. 사이드리얼 해는 태양이 천구의 별에 대해 같은 위치로 돌아가는데 걸리는 시간이다. 과도기는 별들이 매년 경도를 약간 바꾸게 하므로, 실제의 해는 열대 해보다 길다. 히파르쿠스는 분수와 용해의 관측을 이용하여 열대년의 길이가 365+1/4-1/300일 또는 365.24667일(Evans 1998, 페이지 209). 이를 사이드리얼 연도의 길이와 비교해 보면, 그는 한 세기 동안 경과율이 1° 이상이라고 계산했다. 이 정보로부터, 그의 부실 연도의 가치는 365+1/4+1/144일이었다고 계산할 수 있다(토머 1978, 페이지 218). 최소 비율을 제시함으로써 관찰의 오류를 용인하고 있었는지도 모른다.

히파르쿠스는 열대 해를 대략적으로 알기 위해 알마게스트 III.1(Toomer 1984, 페이지 139)의 프톨레마이오스가 설명한 대로 '온인터칼리 월과 일(현재는 손실)'의 메톤과 칼리푸스의 달력을 수정하여 자신만의 루니솔라 달력을 만들었다. 바빌로니아 달력은 기원전 499년(기원전 380년 이전에는 3차례만 예외) 이후 19년 동안 235개월의 음력 주기를 사용했지만, 정해진 일수를 사용하지 않았다. 메토닉 사이클(기원전 432년)은 이 19년에 6,940일을 할당하여 365+1/4+1/76 또는 365.26316일의 평균 연도를 산출하였다. 캘리픽 사이클(기원전 330년)은 365+1/4 또는 365.25일의 평균 연도의 네 번의 메토닉 사이클(76년)에서 하루 하락했다. 히파르쿠스는 4번의 칼리픽 사이클(304년)에서 하루 더 떨어져 365+1/4-1/304 또는 365.24671일의 히파르치 사이클을 만들었는데, 이는 365+1/4-1/300이나 365.24667일이라는 열대해에 가까웠다.

히파르쿠스의 수학적 서명은 기원전 2세기 고대 천문학적 컴퓨터인 안티키테라 메커니즘에서 발견된다. 이 메커니즘은 태양년, 즉 메토닉 사이클(Metonic Cycle)을 기반으로 하고 있는데, 달이 같은 위상을 가지고 하늘의 같은 위치에 다시 나타나는 기간(완전한 달이 대략 19년)이며 칼리픽 사이클(Metonic Cycle, 보다 정확한 4 Metonic Cycle), 사로스 사이클과 엑셀리그모스 사이클(Exeligos 3개)이다. 정확한 일식 예측을 위한 주기). 안티키테라 메커니즘의 연구는 고대인들이 하늘의 태양과 달의 움직임의 모든 측면을 바탕으로 매우 정확한 달력을 사용해왔다는 것을 증명한다. 실제로 앤티키테라 메커니즘의 일부인 달 메커니즘은 일정 시간 동안 달의 움직임과 그 위상을 묘사하는데, 케플러의 제2법칙에 매우 근접한 가변 달 속도를 제공하는 핀과 슬롯 장치가 달린 4단 기어의 열차를 이용한다. 즉, 페리기와 sl에서 달의 빠른 움직임을 고려한다.어포게이지로 동작하다 이 발견은 히파르쿠스가 케플러의 제2법칙에 대한 좋은 근사치를 개발한 것이 분명하기 때문에 프톨레마이오스가 그의 책에서 기술한 것보다 훨씬 더 진보했음을 증명한다.

미트라 별자리

구어적으로 미트라주의라고도 알려진 미트라어 미스터리는 로마 신 미트라의 1-4세기 신 플라토닉 미스터리 컬트였다. 거의 완전한 서면 서술이나 경전이 부족하기 때문에 미트라이어 사원(현대에 미트라이아라고 불림)에서 발견되는 것과 같은 고고학적 증거로부터 믿음과 실천의 재구성이 필요하다. 이는 우주를 대표하는 진짜 혹은 인공적인 "단"이었다. 1970년대까지 대부분의 학자들은 프란츠 쿠몬트를 추종하여 미트라를 페르시아의 신 미트라의 연속이라고 식별했다. 커몬트의 연속성 가설, 그리고 점성술적 요소가 늦고 중요하지 않은 점성술적 점성술이라는 그의 일치 이론은 더 이상 지켜지지 않는다. 오늘날, 이 종교와 그 신앙은 이미 매우 점성술 중심적인 로마 신앙이 일반적으로 그랬던 것보다 훨씬 더 크게 점성술적 요소를 지닌 로마 사상의 산물로 인식되고 있다. 그러나 그 세부사항들은 논의되고 있다.^[16]

축전행위에 관한 한, 미트라교의 한 학자 데이비드 울란지는 ^[16]미트라를 전행의 책임이 있는 힘의 의인화라고 해석했다. 그는 이 숭배는 히파르쿠스의 전분해 발견에 대한 종교적 반응이었으며, 이는 고대 지질학적 관점에서 볼 때, 우주 전체(즉 고정된 별의 가장 바깥쪽 천구)가 이전에 알 수 없는 방식으로 움직이고 있다는 발견에 상당했다고 주장한다. 그의 분석은 미트라 신전의 중심부에 있던 황소를 죽이는 미트라스의 모습이라는 이른바 '타우록토니'에 바탕을 두고 있다. 표준 타우록토니에서는 미트라와 황소가 개, 뱀, 까마귀, 전갈을 동반하고 있다. 울란지에 따르면 타우록토니는 스타 차트다. 황소는 12궁도의 별자리인 황소자리 입니다. In the astrological age that preceded the time of Hipparchus, the vernal equinox had taken place when the Sun was in the constellation of Taurus, and during that previous epoch the constellations of Canis Minor (The Dog), Hydra (The Snake), Corvus (The Raven), and Scorpius (The Scorpion)—that is, the constellations that correspond to the animals d타우록토니로 인식되는—모두 천적도 위에 놓여 있었고, 따라서 그 시대 동안 하늘에서 특권적 위치를 가지고 있었다. 미트라스 자신은 페르세우스 별자리를 나타내며, 이 별자리는 미트라가 타우록토니 이미지에서 차지하는 위치인 황소자리 타우루스 바로 위에 위치한다. 미트라스가 황소를 죽인 것은, 이 추리에 의해 이 새로운 신이 가지고 있는 힘을 나타내어 우주구역을 돌려서 춘분의 위치가 황소를 죽이는 것으로 상징되는 황소자리(황소를 죽이는 것으로 상징되는 과도기)를 남겼고, 개, 뱀, 라벤, 스콜피온 등도 마찬가지로 테이를 잃었다.천적도의 특권적 ^[16]위치

또한 아이콘그래피에는 두 명의 성화 봉송 쌍둥이가 황소 슬레이잉 이미지를 액자화하여 있는데, 하나는 횃불을 들고 다른 하나는 아래를 가리키는 횃불을 들고 있다. 이 성화 봉송자들은 때때로 그들 중 한 명이 황소와 잎이 있는 나무와 연관되거나, 다른 한 명은 스콜피온과 열매가 있는 나무와 연관되어 묘사된다. 울란지는 이러한 횃불베어들이 황소리와 전갈피우스에서 각각 춘분(토크업, 잎이 있는 나무, 불)과 추분(토크업, 과일이 있는 나무, 스콜피온)을 나타내는 것으로 해석하고 있는데, 이 때는 전체적으로 타우루스 시대(Age of Taurus)에 상징되는 앞선 '타우루스(Age of Taurus)' 때 분수가 위치했던 곳이다. 이리하여 울란지는 미트레이어적 우상이란 새로운 우주적 신성의 존재가 비밀이었던 '우주적 코드'라고 결론짓고, 그의 근본적인 속성은 전체 우주의 구조를 변화시키고 그에 따라 인간의 존재를 결정하기 위해 그 당시 믿었던 점성학적 힘을 통제하는 능력이었다.그러므로 그에게 헌신적인 사람들에게 삶 동안 성공하고 죽은 후의 구원을 허락할 수 있는 힘을 준다(즉, 행성계를 통한 안전한 여행과 그 후 별들의 영역에서 불멸의 존재를 부여한다.^[16]

전봇대 별 바꾸기

그 전착의 결과는 변화하는 극성이다. 현재 폴라리스(Polaris)는 북극의 위치를 표시하기에 매우 적합하며, 폴라리스(Polaris)는 시각적 규모 2.1(변수)의 적당히 밝은 별이며, 극으로부터 약 1도 떨어져 있으며, 밝기가 비슷한 별은 너무 가까이 있지 않기 때문이다.^[17]

이전의 극성별은 폴라리스에서 16도에 위치한 '리틀 디퍼'의 그릇에서 가장 밝은 별인 코차브(베타 우르새 미노리스, β UMI, β 우르새 미노리스)이다. 그것은 기원전 1500년부터 AD 500년까지 그 역할을 담당했다.^[18] 그것은 오늘날 폴라리스만큼 정확하지 않았다.^[18] 오늘날, 코합과 그 이웃인 페르카드는 "극의 수호자"(폴라리스라는 뜻)라고 불린다.^[18]

반면 기원전 3000년 극성이었던 드라코 별자리의 투반은 진도 3.67(폴라리스의 1/5만큼 밝음)에서는 눈에 잘 띄지 않는다. 오늘날은 빛으로 오염된 도시 하늘에서는 보이지 않는다.

폴라리스가 2만7,800년경에 다시 북극성이 되면, 폴라리스가 적절한 움직임 때문에 지금보다 더 극에서 멀어질 것이고, 기원전 2만3,600년 폴라리스가 극에 가까워졌다.

그 지역은 하늘의 특히 싱거운 부분이고, 명목상의 남극별은 이상적인 조건에서도 거의 육안으로 볼 수 없는 시그마 옥탄티스(Sigma Octantis)이기 때문에 지금 이 순간 하늘에서는 남극을 찾기가 더 어렵다. 그러나 그것은 80세기에서 90세기에 걸쳐서, 남극의 천체가 거짓 십자가를 통해 이동하게 될 때 바뀔 것이다.

이런 상황은 별지도에서도 볼 수 있다. 남극의 방향이 남십자성 쪽으로 이동하고 있다. 지난 2000여 년 동안 남십자사는 남극의 천체를 가리켜 왔다. 그 결과, 이 별자리는 고대 그리스 시대와 달리 아열대 북부 위도에서 보기 어렵다. 남십자사는 마이애미(약 25N)만큼 북쪽 먼 곳에서도 볼 수 있지만 겨울/초봄에만 볼 수 있다.

극지교대 및 분점교대

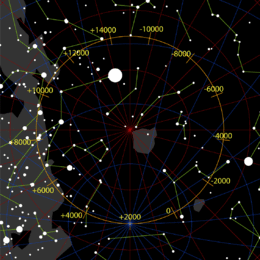
오른쪽의 이미지들은 지구 축의 전열과 춘분의 변화 사이의 관계를 설명하려고 시도한다. 이 이미지들은 실제 거리와 상관없이 지구에서 본 것처럼 별들을 그들의 위치에 따라 배치하는 가공의 구체인 천체 위에 지구 축의 위치를 보여준다. 첫 번째 이미지는 외부에서 온 천체를 보여주는데, 거울상에는 별자리가 그려져 있다. 두 번째 이미지는 매우 넓은 각도 렌즈를 통해 볼 수 있는 근지구 위치의 원근법을 보여준다.

지구의 자전축은 2만5700년의 기간에 걸쳐 도표 상단에 가까운 항성들 사이의 작은 푸른 원을 묘사하고 있는데, 이 원은 황색성 북극(파란 문자 E)을 중심으로 하고, 각 반지름은 약 23.4°로, 황색성의 난각도로 알려져 있다. 전처리 방향은 지구가 축 위에서 매일 회전하는 방향과 반대다. 갈색 축은 5000년 전 지구의 자전 축으로, 투반 별을 가리켰다. 폴라리스(Polaris)를 가리키는 노란색 축이 지금 축을 표시한다.

천적도가 황도(적색선), 즉 지구의 축이 태양과 지구의 중심을 연결하는 선에 수직인 곳에서 발생하는 등분. (여기서 "등분"이라는 용어는 태양이 적도에서 머리 위에 있는 순간이라기 보다는 그렇게 정의된 천구상의 점을 가리킨다는 점에 유의한다.) 비록 두 가지 의미가 연관되어 있지만) 축이 한 방향에서 다른 방향으로 진행되면 지구의 적도면(적도 주위의 원형 격자로 표시됨)이 움직인다. 천적도는 단지 천구에 투영된 지구의 적도일 뿐이므로 지구의 적도면이 움직이면서 움직이며, 황도와의 교차점이 그와 함께 움직인다. 지구의 극과 적도의 위치는 변하지 않고 고정된 별에 대한 지구의 방향만 바뀐다.

5000년 전 갈색 격자에서 보듯이 춘분은 황소자리에 있는 별 알데바란과 가까웠다. 이제 황색 격자에서 보듯이, 그것은 (붉은 화살표로 표시) 물고기자리 어딘가로 이동했다.

여전히 이와 같은 그림은 첫 번째 근사치일 뿐인데, 이는 경과속도의 가변 속도, 황반변성의 가변성, 행성의 전열(현재 비행기에 위치한 축을 중심으로 경도 174.8764°)을 고려하지 않기 때문이다. 그리고 별들의 적절한 움직임.

흔히 "위대한 달"이라고 알려져 있는 각 별자리의 경과가 아래 표에 대략적으로 나타나 있다.^[19]

별자리	근사년
	들어가는	종료 중
황소자리	기원전 4500년	기원전 2000년
양자리	기원전 2000년	기원전 100년
물고기자리	기원전 100년	2700 CE

원인

이분류의 전과는 태양과 달의 중력, 그리고 지구상의 다른 신체들에 의해 일어난다. 그것은 처음에 아이작 뉴턴 경에 의해 설명되었다.^[20]

축전극은 회전하는 팽이의 전극과 유사하다. 두 경우 모두 적용된 힘은 중력에 기인한다. 회전 상단의 경우 이 힘은 처음에는 회전 축과 거의 평행하는 경향이 있으며, 상단의 속도가 느려질수록 증가한다. 스탠드의 자이로스코프는 90도에 도달할 수 있다. 그러나 지구에서는 태양과 달의 작용력이 자전축에 수직에 가깝다.

지구는 완벽한 구체는 아니지만, 극지름보다 약 43km나 더 큰 적도 직경을 가진 섬광선이다. 지구의 축방향 기울기 때문에, 일년 중 대부분 동안 태양에 가장 가까운 이 돌출부의 절반은 북쪽이나 남쪽의 중심에서 벗어나고, 나머지 절반은 반대편의 중심에서 벗어난다. 거리의 사각형과 함께 중력이 감소하기 때문에 지구 반대쪽보다 태양이 더 강하게 끌어당기면서 지구에 작은 토크가 생성된다. 이 토크의 축은 대략 지구의 자전 축에 수직이기 때문에 자전 축이 미리 처리된다. 만약 지구가 완벽한 구체였다면, 어떠한 전열도 없을 것이다.

이 평균 토크는 회전축이 촉각극으로부터 멀리 기울어지는 방향에 수직이 되어 축방향 틸트 자체를 바꾸지 않는다. 태양(또는 달)에서 나오는 토크의 크기는 지구의 스핀 축 방향과 중력 끌어당김 방향 사이의 각도에 따라 달라진다. 그들이 수직일 때 그것은 0에 접근한다. 예를 들어 태양과의 교호작용의 경우, 이 일은 분분에 일어난다. 이는 근거리와 원점이 중력 인력과 일직선상에 있기 때문에 중력 인력의 차이로 인한 토크가 없기 때문이라고 볼 수 있다.

위의 설명이 태양을 포함하긴 했지만, 지구 주위를 움직이는 물체, 특히 달과 함께 또는 가까이 움직이는 물체에 대해서도 동일한 설명이 적용된다. 태양과 달의 결합 작용을 루니솔라 전치라고 한다. 꾸준한 진행 운동(약 2만5천700년 만에 완전한 원을 그리게 됨) 외에도, 태양과 달은 그들의 위치 변화로 인해 작은 주기적 변화를 야기한다. 이러한 진동은 전처리 속도와 축 틸트 모두에서 너트라고 알려져 있다. 가장 중요한 용어의 기간은 18.6년이고 진폭은 9.2 아크초이다.^[21]

태양계의 다른 행성들의 작용으로 황반 전극 외에도 황반 전체가 순간 황반으로 측정된 황반경도 약 174°의 축을 중심으로 천천히 회전하게 된다. 소위 행성적 전처리 전환이라고 하는 이 시프트는 연간 0.47초(루니솔라 전처리보다 100배 이상 작은)의 황반면을 회전시키는 것에 해당한다. 두 가지 경과의 합은 일반적인 경과라고 알려져 있다.

방정식

동요하는 몸체(태양, 달 또는 행성)로 인한 지구상의 조력(조력)은 뉴턴의 만유인력의 법칙에 의해 표현되는데, 여기서 가장 가까운 지구의 변에 동요하는 몸의 중력이 거리의 입방체 차이에 비례하는 양만큼 먼 쪽의 중력보다 더 크다고 한다.s 가까운 쪽과 먼 쪽 사이 지구 중심에 점 질량(궤도 운동을 일으키는 구심력을 제공하는)으로서 지구의 질량에 작용하는 동요체의 중력을 지구 표면의 모든 곳에 있는 동요체의 중력에서 빼낸다면, 남아 있는 것은 조력이라고 볼 수 있다. 이것은 위성을 멀리하는 힘이라는 역설적인 개념을 주지만 실제로는 중력장의 구배 때문에 그 몸을 향한 힘이 더 작을 뿐이다. 이 조력은 전과를 위해 평균 구형 반지름 바깥의 적도 돌출부에만 작용하는 두 개의 힘으로 분류될 수 있다. 이 커플은 두 쌍의 구성 요소로 분해될 수 있는데, 하나는 서로 상쇄되는 동요하는 몸체를 향해 지구 적도 평면에 평행하고 다른 한 쌍은 지구의 회전 축에 평행하며 둘 다 황화면을 향해 분해될 수 있다.^[22] 후자의 한 쌍의 힘은 지구의 적도 돌출부에 다음과 같은 토크 벡터를 생성한다.^[4]

${\displaystyle {\overrightarrow {T}={\frac {3}GM}{r^{3}}}(C-A)\sin \delta \cos \delta \delta {\begin{pmatrix}\sin \alpha \\\\cos \alpha \\\\0\end{pmatrix}}}}}}}}}}$

어디에

GM, 비틀거리는 몸의 표준 중력 파라미터

r, 동요하는 몸체에 대한 지리학적 거리

C, 지구 회전 축 주위의 관성 모멘트

A, 지구의 적도 직경 주위의 관성 모멘트

C - A, 지구 적도 돌출부의 관성 모멘트(C > A)

Δ, 동요하는 몸체(적도의 북쪽 또는 남쪽)의 수축

α, 동요하는 몸의 우측 상승(춘분에서 동쪽으로).

지구 중심에 있는 토크의 세 단위 벡터(위아래)는 춘분을 향하는 황반면(지구 적도면과 황반면의 교차점) 내의 선에 x, 하지를 향한 황반면(x의 동쪽 90°)의 선에 y, 그리고 z는 th를 향한 선에 있다.e 황반 북극

태양의 x 방향(sinΔ cosΔ sinα)의 세 사인 항 값은 분점(0°, 180°)에서 0부터 변화하는 사인 제곱 파형이다. 용액에서 0.36495까지(90°, 270°) The value in the direction of y (sinδ cosδ (−cosα)) for the Sun is a sine wave varying from zero at the four equinoxes and solstices to ±0.19364 (slightly more than half of the sine squared peak) halfway between each equinox and solstice with peaks slightly skewed toward the equinoxes (43.37°(−), 136.63°(+), 223.37°(−), 316.63°(+)). 두 태양 파형은 피크 대 피크 진폭과 동일한 기간, 즉 1년의 절반 또는 반년의 동일한 기간을 가진다. z 방향의 값은 0이다.

y 방향의 사인파의 평균 토크는 태양이나 달의 경우 0이므로, 토크의 이 성분은 사전 처리에 영향을 주지 않는다. 태양 또는 달의 x 방향에서 사인 제곱 파형의 평균 토크는 다음과 같다.

${\displaystyle T_{x}={\frac {3}{2}}:{\frac {GM}{a^{3}\왼쪽(1-e^{2}\오른쪽)^{\frac {3}{3}2}}(C-A)\sin \epsilon \epsilon}}}}$

어디에

$지구(태양$) 궤도 또는 달의 궤도의 반(半)조르한 축$.$

e, 지구(태양) 궤도 또는 달의 궤도 이심률

그리고 사인의 평균을 1/2계정 파형, 3(1− e2)32{\displaystyle a^{3}(1-e^{2}\right)^{\frac{3}{2}}}지구에서 전체 타원형 orbit,[23]과ε(적도 면과 황도 면 사이의 각도)의 평균 거리는 태양이나 달의 세제곱은 1에 대한를 차지할 자세를 취하였다.맥스.전체 18.6년 주기 동안 태양의 Δ와 달의 평균 최대값의 imum 값.

사전 처리:

${\dplaystyle {\frac {d\psi }{dt}={\frac {T_{x}{C\omega \sin \엡실론}}}}$

여기서 Ω은 지구의 각속도, Ω은 지구의 각운동량이다. 따라서 태양에 의한 전이의 첫 번째 순서는 다음과 같다.^[4]

${\dplaystyle {\frac {d\psi_{S}{dt}={\frac {3}{2}}\좌측[{\frac {GM}{a^{3}\좌측(1-e^{2}\우측)^{\frac {3}{2}}\우측]^{\frac {}}{S}\왼쪽[{\frac {C-A}{C}}}{\frac {\c}}\cos \cos \epsilon }{\omega }\right]_{E}$

반면에 달로 인한 것은 다음과 같다.

${\displaystyle {\frac {d\psi _{{dt}={\frac {3}{2}}\왼쪽[{\frac {GM\왼쪽(1-1.5\sin ^{2}i\오른쪽)}}{a^{3}\왼쪽(1-e^{2}\오른쪽)^{\frac {3}{2}}:\오른쪽]_{L}\왼쪽[{\frac {C-A}{C}}}{\frac {\c}}\cos \cos \epsilon }{\omega }\right]_{E}$

여기서 나는 달의 궤도면과 황색면 사이의 각도다. 이 두 방정식에서 태양의 매개변수는 S로 표시된 대괄호 안에 있고, 달의 매개변수는 L로 표시된 대괄호 안에 있으며, 지구의 매개변수는 E로 표시된 대괄호 안에 있다. $({\displaystyle 1\mathrm{}\mathrm{}}$- ${\displaystyle 1}$.5 ${\displaystyle {\sin }^{}}$ ${\displaystyle 2}$ ${\displaystyle {}^{}}$ i${\displaystyle }$) ${\$라는 용어는 황색에 상대적인 달 궤도의 기울기를 설명한다$$. 용어 (C - A)/C)는 지구의 동적 타원성 또는 평탄화로서, 지구의 내부 구조가 충분히 상세하게 알려져 있지 않기 때문에 관측된 전열에 따라 조정된다. 만약 지구가 균질하다면 용어는 세 번째 편심 제곱과 같을 것이다.^[24]

${\displaystyle e'^{2}={\frac {\mathrm {a}^{2}-\mathrm {c}^{2}}:{{2}-\mathrm {a}^{2}+\mathrm {c}^{2}}:$

여기서 a는 적도 반지름(6378137m)이고 c는 극 반지름(6356752m)이므로 e = 0².003358481이다.

7자리수(선행 1 제외)로 반올림된 J2000.0에 적용할 수 있는 매개변수는 다음과 같다.^[25][26]

태양	달	지구
GM = 1.3271244×10m203/s2	GM = 4.902799×10m123/s2	(C − A)/C = 0.003273763
a = 1.4959802×10m11	a = 3.833978×10m8	Ω = 7.292115×10−5 rad/s
e = 0.016708634	e = 0.0555453	ε = 23.43928°
	i = 5.15690°

어느 것이 생산되는가

dd_S/dt = 2.450183×10⁻¹² /s

dd_L/dt = 5.334529×10⁻¹² /s

이 두 가지는 모두 //a (arcseconds/annum)로 변환되어야 하며, 2㎛ 라디안의 아크초 수(1.296×10⁶″/2π)와 1 Annum의 초 수(Julian 연도)(3.15576×10s⁷/a)로 변환되어야 한다.

dd_S/dt = 15.948788″/a 대 윌리엄스^[4] 15.948870″/a

dd_L/dt = 34.723638″/a 대 윌리엄스의 34.457698″/a.

태양 방정식은 지구의 궤도가 타원에 가깝기 때문에 다른 행성들에 의해 약간 혼란스러울 뿐이기 때문에 태양에 의한 전이를 잘 나타낸다. 달 방정식은 달의 궤도가 태양에 의해 크게 왜곡되고 일년에 걸쳐 반지름이나 편심도 일정하지 않기 때문에 달로 인한 전이를 잘 표현하지 못한다.

가치

19세기 말 사이먼 뉴콤의 경도 일반적 전열(p)에 대한 계산은 열대 세기 당 5,025.64 아크초의 값을 주었으며, 인공위성이 보다 정확한 관측을 전달하고 전자 컴퓨터가 더 정교한 모델을 계산할 수 있을 때까지 일반적으로 받아들여진 값이었다. Jay Henry Lieske는 1976년에 업데이트된 이론을 개발했는데, 여기서 p는 줄리안 세기당 5,029.0966 아크초(1.3969713도)와 같다. VLBI와 LLR과 같은 현대적 기법은 추가적인 정비를 허용했고, 국제천문연맹은 2000년에 새로운 상수값을 채택했고, 2003년과 2006년에 새로운 계산법과 다항식 표현식을 채택했다. 누적된 사전 처리량은 다음과 같다.^[27]

p_A = 5,028.796195 T + 1.1054348 T² + 고주문 조건,

arcseconds, T와 함께, 2000년 시대 이후 줄리안 세기(즉, 36,525일)의 시간.

경과율은 그 파생상품이다.

p = 5,028.796195 + 2.2108696 T + 고차 항.

이 속도의 상수 기간(위 방정식의 세기당 5,028.796195 아크초)은 다른 일부 출처가 값을 25771.4년으로 설정하여 약간의 불확실성을 남기지만, 25,771.57534년(세기로 360도 분할된 하나의 완전한 원)^[27]에 해당한다.

경과율은 상수가 아니라 T의 선형(및 더 높은 순서) 항으로 나타내듯이 시간이 지남에 따라 서서히 증가하는 (현재)이다. 어떤 경우에도 이 공식은 제한된 기간 동안만 유효하다는 점을 강조해야 한다. 그것은 태양계의 결정론적 모형이 아닌 관측 데이터에 경험적으로 적합된 J2000 기준점을 중심으로 한 다항식이다. T가 충분히 커지면(먼 미래나 먼 과거) T² 용어가 지배하고 p가 매우 큰 값으로 갈 것이 분명하다. 실제로 태양계의 수치모델에 대한 보다 정교한 계산은 전치 상수의 기간이 약 4만 1천 년이라는 것을 보여주는데, 이는 황혈의 난치도와 같다. 여기에 언급된 상수는 전처리 자체가 아니라 위의 공식의 선형 및 모든 상위 용어라는 점에 유의하십시오. 그것은

p = A + BT + CT² + …

의 근사치 입니다.

p = a + b 죄(2 sinT/P), 여기서 P는 41,000년 기간이다.

이론적 모델은 T의 높은 힘에 해당하는 상수(관용)를 계산할 수도 있지만, (마인드) 다항식이 모든 숫자에 걸쳐 주기 함수를 일치시키는 것은 불가능하므로, T가 증가함에 따라 그러한 모든 근사치의 차이는 구속되지 않고 커질 것이다. 그러나 반드시 불완전한 동적 수치 모델이 아니라 관측 데이터에 충분한 수의 다항식을 적합시킴으로써 제한된 시간 범위에 걸쳐 더 큰 정확도를 얻을 수 있다. 그래서 현재 인공위성과 우주선의 비행 궤적 계산에 있어서 다항식 방법은 더 나은 정확도를 준다. 그런 점에서 국제천문연맹은 가장 잘 발달된 가용이론을 택했다. 과거와 미래에서 최대 몇 세기 동안 모든 공식은 크게 달라지지 않는다. 과거와 미래에서 최대 몇 천년 동안, 대부분은 어느 정도 정확성에 동의한다. 더 멀리 떨어져 있는 시대의 경우 불일치가 너무 커진다 – 정확한 경과율과 경과 기간은 단 하나의 전체 경과 기간에도 이러한 다항식을 사용하여 계산되지 않을 수 있다.

지구 축의 전열은 매우 느린 효과지만 천문학자들이 일하는 정확도 수준에서는 매일 고려할 필요가 있다. 주의할 점은 지구 축의 전열과 기울기(경락성의 직각성)는 같은 이론에서 계산되어 서로 연관되어 있지만, 두 운동은 서로 독립적으로 작용하여 반대 방향으로 움직인다는 것이다.

현재를 중심으로 5억 년 동안 59"/a에서 45"/a (a = Annum = Julian year)까지의 조수 방전으로 인해 세속적인 감소가 나타난다. 단기 변동(수천년)을 평균화한 후, "/a, T가 수십억 줄리앙 년(Ga)에 있는 경우, 현재로부터 음과 양의 시간에 대해 다음과 같은 다항식으로 장기 추세를 근사할 수 있다.^[28]

p⁻ = 50.475838 - 26.36883 T + 21.890862² T

p⁺ = 50.475838 - 27.000654 T + 15.6032655² T

사전 처리량은 +30Ma에서 +130Ma 사이의 작은 양인 +0⁺.135052"/a보다 클 것이다. 세속적인 진행의 감소가 다른 행성들에 의해 야기된 지구 궤도의 공명을 가로지르기 시작했기 때문에 p에⁺ 대한 이 초과 점프는 이제 겨우 20 Ma에서 일어날 것이다.

워드에 따르면 약 1500만년 만에 조석효과로 인해 지속적으로 증가하고 있는 달의 거리가 현재의 60.3년에서 약 66.5지구반경으로 증가했을 때, 행성효과로 인한 공진은 처음에는 4만9000년으로, 그 후 달이 약 2000mi에 68지구반경에 이르면 지구반도를 앞당길 것이다.6만 9천 년까지. 이것은 또한 황혈의 부피에 있는 야생의 그네와도 관련이 있을 것이다. 그러나 워드는 비정상적으로 큰 현대적 가치를 조수 방산에 사용했다. 현대적 가치의 약 절반인 조석 리듬이 제공하는 6억 2천만 년의 평균을 사용한다면, 이러한 공명들은 각각 약 3,000만 년과 4,000만 년까지 도달하지 못할 것이다. 그러나, 점차적으로 증가하는 태양의 광도 때문에, 지구의 바다는 그 시간 이전에 기화되었을 것이다(지금으로부터 약 21억 년 후).

참고 항목

• 물병자리 시대
• 점성술 연령
• 천문 영양학
• 축 기울기
• 오일러 각도
• 춘분 경도
• 밀란코비치 주기
• 부성년

참조

참고 문헌 목록

외부 링크

Wikisource는 The New Student's Reference Work 기사 "Precession"의 본문을 가지고 있다.

• 달랑베르트와 오일러의 이분법 해결 논의
• Bowley, Roger; Merrifield, Michael. "Axial Precession". Sixty Symbols. Brady Haran for the University of Nottingham.
• 지구의 강제적인 전처리 및 견과