이십면체
Icosahedron
기하학에서 20면체(/ˌaɪkɒsəhiːdrən, -k--, -kʊ-/ 또는 /aɪkssəhiːdrnn/)[1]는 20개의 면을 가진 다면체이다.The name comes from Ancient Greek εἴκοσι (eíkosi) 'twenty' and from Ancient Greek ἕδρα (hédra) ' seat'.복수형은 "icosaheadra"(/-dr//) 또는 "icosaheadrons"일 수 있다.
이코사면에는 매우 많은 유사하지 않은 모양들이 있는데, 그 중 일부는 다른 것들보다 더 대칭적이다.가장 잘 알려진 것은 (볼록형, 비강형) 정이십면체이며, 이십면체는 플라톤의 고체 중 하나이며, 면은 20개의 정삼각형이다.
정이십면체
 볼록 정이십면체 |  대이십면체 |
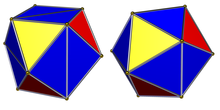
볼록한 것과 볼록하지 않은 것의 두 가지가 있으며, 둘 다 정이십면체라고 할 수 있다.각 모서리는 30개의 모서리와 20개의 정삼각형 면을 가지며, 12개의 꼭지점 각각에 5개의 정점이 있습니다.둘 다 정십면체 대칭을 가지고 있다."정규 이십면체"라는 용어는 일반적으로 볼록한 다양성을 말하는 반면, 비볼록 형태는 위대한 이십면체라고 불립니다.
볼록 정이십면체
볼록한 정이십면체는 보통 5개의 정육면체 중 하나인 정육면체라고 불리며, 각 정점에서 5개의 면이 만나는 20개의 삼각형 면을 포함하는 슐레플리 기호 {3, 5}으로 표현된다.
그것의 이중 다면체는 각 꼭지점 주위에 세 개의 정다각형 면을 가진 정십이면체 {5,3}이다.
대이십면체
거대한 20면체는 케플러-포인소트 다면체 4개의 규칙적인 별 중 하나이다.Schléfli 기호는 {3}입니다.볼록한 형태와 마찬가지로 20개의 정삼각형 면을 가지지만 정점 도형은 오각형이라기보다 오각형이어서 기하학적으로 교차하는 면이 있다.삼각형의 교차로는 새 모서리를 나타내지 않습니다.
그것의 이중 다면체는 각 꼭지점 주위에 세 개의 규칙적인 별 오각형 면을 가진 거대한 스텔레이트 십이면체 {5/2,3}입니다.
이코사헤드라
단정은 다면체의 면이나 모서리를 새로운 다면체를 형성하기 위해 만날 때까지 연장하는 과정이다.이는 대칭적으로 수행되므로 결과 도형이 상위 도형의 전체 대칭을 유지합니다.
그들의 책 59 이코사헤드라, 콕서터 외.정십면체의 58개의 그러한 층계를 열거했다.
이 중 많은 것들이 20개의 면 평면에 각각 하나의 면을 가지고 있으며, 또한 이코사면도 마찬가지이다.거대한 20면체가 그들 중에 있다.
다른 용골은 각 평면에 둘 이상의 면을 가지거나 더 단순한 다면체의 화합물을 형성한다.이것들은 엄밀하게는 이코사면이라고 할 수 없지만, 종종 그렇게 언급된다.
| 이십면체의 주목할 만한 특징 | |||||||||
| 규칙적인. | 균일한 이중화 | 규칙 화합물 | 정규성 | 다른이들 | |||||
| (볼록) 20면체 | 작은 삼암면체 20면체 | 중앙 삼암면체 | 대삼각형 정십이면체 | 오팔면체 화합물 | 5개의 사면체 화합물 | 10개의 사면체 화합물 | 대이십면체 | 출토된 12면체 | 최종 단계 |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| 20면체에서의 계단화 과정은 다수의 관련된 다면체와 20면체 대칭을 가진 화합물을 생성한다. | |||||||||
사면체 대칭
| 정면체 대칭 및 정면체 대칭 | |||||
|---|---|---|---|---|---|
| 콕서터 도표 | |||||
| 슐레플리 기호 | s{3,4} sr {3,3} s { { s { \ {} \ \ \ { } } | ||||
| 얼굴 | 20개의 삼각형: 8 등변 12개의 이등분 | ||||
| 가장자리 | 30 (짧은 길이 6 + 긴 길이 24) | ||||
| 꼭지점 | 12 | ||||
| 대칭군 | Th, [4,3+], (3*2), 주문 24 | ||||
| 로테이션 그룹 | Td, [3,3],+ (332), 순서 12 | ||||
| 이중 다면체 | 열면체 | ||||
| 특성. | 볼록한 | ||||
 그물 | |||||
| |||||
정이십면체는 변형되거나 낮은 열면체 [2]대칭으로 표시될 수 있으며, 스너브 팔면체, 스너브 사면체, 스너브 사면체, 의사 이십면체라고 불립니다.이것은 교대로 잘린 팔면체로 볼 수 있다.모든 삼각형이 등변일 경우 8과 12의 삼각형을 다르게 색칠하여 대칭을 구별할 수도 있습니다.
열면체 대칭은 (3*2), [3+,4]의 차수가 24인 기호입니다.사면체 대칭의 기호는 (332), [3,3]+이고 차수는 12입니다.이러한 하위 대칭은 20개의 정삼각형 면으로부터 기하학적 왜곡을 허용하며, 대신 8개의 정삼각형과 12개의 일치된 이등변 삼각형을 가집니다.
이 대칭들은 콕서터 다이어그램을 제공한다: 그리고 각각은 규칙 20면체, (*532), [5,3] 순서 120의 20면체 대칭에 대한 낮은 대칭을 나타낸다.
데카르트 좌표

12개의 정점의 좌표는 가능한 모든 순환 순열 및 형식(2, 1, 0)의 좌표 부호 플립에 의해 정의된 벡터로 정의할 수 있습니다.이러한 좌표는 교대 정점이 삭제된 잘린 8면체를 나타냅니다.
이 구조는 정이십면체 형태의 스누브 사면체라고 불리며, 벡터(θ, 1, 0)에서 시작하여 수행되는 동일한 연산에 의해 생성되며, 여기서 θ는 [2]황금비이다.
제센의 20면체
때때로 제센의 직교 이십면체라고 불리는 제센의 이십면체에서, 12개의 이등변면은 볼록하지 않고 직각 이면각을 가지도록 다르게 배열되어 있다.
그것은 큐브와 일치하는 가위이며, 이것은 단단한 큐브를 만들기 위해 재배열할 수 있는 더 작은 다면체 조각으로 잘라질 수 있다는 것을 의미합니다.
육팔면체
정이십면체는 6개의 정사각형 면이 열면체 대칭을 가진 대각선 위에 양분된 정육면체와 위상적으로 동일하다.이십면체 대칭을 가진 이십면체는 정팔면체, 정이십면체, 제센의 이십면체, 이중 덮개 팔면체를 포함하는 무한 다면체군을 구성한다.이 패밀리의 구성원들 사이에 주기적인 운동학적 변환이 존재합니다.
기타 정육면체
마름모꼴 20면체
마름모꼴 20면체는 20개의 합동 마름모꼴로 이루어진 조면체이다.그것은 10개의 중간면을 제거함으로써 마름모꼴 3면체에서 파생될 수 있다.모든 면들이 일치하더라도, 마름모꼴의 20면체는 면 전이성이 없다.
피라미드와 프리즘의 대칭
피라미드와 프리즘 대칭을 가진 일반적인 이코사면체는 다음과 같습니다.
- 19면 피라미드(+ 1 베이스 = 20).
- 18면 프리즘(+2단=20).
- 9면 반작용(9면 2세트 + 2단 = 20).
- 10면 이원체(10면 2세트 = 20).
- 10면 3면체(10면체 2세트 = 20).
존슨 고체
| J22 | J35 | J36 | J59 | J60 | J92 |
|---|---|---|---|---|---|
 자이로롱게 삼각형 큐폴라 |  가늘고 긴 삼각형 직소성 우폴라 |  길쭉한 삼각형 자이로비쿠폴라 |  근배율 12면체 |  메타배율 12면체 |  삼각헤베페노로툰다 |
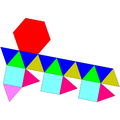 |  | 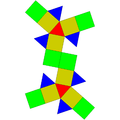 |  |  |  |
| 16개의 삼각형 사각형 3개 육각형 1개 | 8개의 삼각형 12개의 정사각형 12칸 | 8개의 삼각형 12개의 정사각형 12칸 | 10개의 삼각형 10 펜타곤 | 10개의 삼각형 10 펜타곤 | 13개의 삼각형 사각형 3개 펜타곤 3개 육각형 1개 |
「 」를 참조해 주세요.
레퍼런스
- ^ Jones, Daniel (2003) [1917], Peter Roach; James Hartmann; Jane Setter (eds.), English Pronouncing Dictionary, Cambridge: Cambridge University Press, ISBN 3-12-539683-2
- ^ a b John Baez (September 11, 2011). "Fool's Gold".
- ^ 수학세계의 이십면체.