탁탁거리는 소음

크래킹 노이즈는 시스템이 외부의 힘을 받을 때 발생하며 다양한 스케일에서 매우 유사하게 나타나는 이벤트를 통해 반응합니다.고전적인 시스템에는 일반적으로 켜짐과 꺼짐의 두 가지 상태가 있습니다.그러나 때때로 그 사이에 상태가 존재할 수 있습니다.이 소음을 분류할 수 있는 세 가지 주요 범주가 있습니다. 첫 번째 범주는 팝콘과 같이 매우 유사한 크기의 사건이 지속적으로 무작위로 발생하는 팝핑입니다. 두 번째 범주는 임계 임계값을 초과할 때까지 시스템에 거의 변화가 없는 스냅핑입니다. 두 번째 범주는 전체 시스템이 한 상태에서 다른 상태로 전환됩니다.연필을 낮잠을 잔다; 세 번째는 펑펑 소리와 펑펑 소리의 조합인 크래킹이다, 여기에는 그것들의 발생을 예측하는 관계 법칙이 있는,^[1] 보편성이라고 불리는, 약간의 크고 작은 사건들이 있습니다.종이 ^[2]구김, 사탕 포장지(또는 다른 탄성 시트),^[3][4] 화재, 지진 발생 및 강자성 물질의 자화와 같은 많은 자연 현상에서 균열이 관찰될 수 있습니다.

갈라지는 소음은 딸깍거리는 소음 및 터지는 소음과 대조적입니다.스냅 노이즈는 하나의 큰 항복 이벤트인 반면, 팝핑 노이즈는 유사한 크기의 작은 항복 이벤트의 일정한 수준입니다.이것들 사이에 크래킹이 있습니다.이는 시스템 구성 요소 간의 연결 강도가 위험 수준에 있을 때 발생하며, 이로 인해 크기가 여러 ^[5]개의 크기 순서에 걸쳐 있는 많은 산출 이벤트가 발생합니다.

이러한 시스템 중 일부는 자석을 퀴리 ^[6]온도로 가열하는 것과 같이 가역적인 반면, 눈사태(눈이 산 아래로만 이동할 수 있는 곳)와 같이 비가역적인 시스템도 있지만, 많은 시스템은 결국 중력 또는 다른 외부 힘과 같이 한 상태에서 다른 상태로 이동하도록 하는 양의 바이어스를 가지고 있습니다.

이론.

바르크하우젠 잡음

큰 영역 내의 작은 섭동에 대한 연구는 1910년대 후반 하인리히 바르하우젠이 강자성 물질 내의 영역 또는 쌍극자가 외부 자기장의 영향을 받아 어떻게 변화하는지 조사하면서 시작되었습니다.자석이 탈자되면 자석의 쌍극자가 임의의 방향을 가리키기 때문에 모든 쌍극자의 순 자력은 0이 됩니다.철봉을 와이어로 감은 후 전류를 와이어에 통과시킴으로써 코일에 수직인 자기장이 생성됩니다(코일의 경우 플레밍의 오른손 법칙). 이는 자석 내의 쌍극자가 외부 필드에 정렬되도록 합니다.

이러한 도메인이 하나씩 연속적으로 뒤집어지는 것으로 생각되었던 당시의 생각과는 달리, Barkhausen은 도메인 클러스터가 작은 개별 ^[7]단계로 뒤집히는 것을 발견했습니다.스피커 또는 검출기에 연결된 바에 2차 코일을 감음으로써 도메인 클러스터의 정렬이 변경되면 플럭스의 변화가 발생하여 2차 코일의 전류가 중단되어 신호 출력이 발생합니다.큰 소리로 재생될 때 이를 바크하우젠 노이즈라고 하며, 자석의 자화는 플럭스 ^[8]밀도의 함수로 별개의 단계로 증가합니다.

구텐베르크-리히터 법칙

지진을 분석적으로 조사한 찰스 프랜시스 리히터와 베노 구텐베르크에 의해 1940년대 후반에 탁탁거리는 소음에 대한 추가적인 연구가 이루어졌습니다.잘 알려진 리히터 규모가 발명되기 전에는 메르칼리 강도 척도가 사용되었습니다. 이것은 지진이 재산에 얼마나 피해를 주었는지에 대한 주관적인 측정입니다.II는 작은 진동과 물체가 움직이는 반면 XII는 모든 건물의 광범위한 파괴가 될 것입니다.리히터 스케일은 지진의 진원지에서 발산되는 진동의 에너지와 진폭을 측정하는 로그 스케일입니다. 즉, 7.0 지진은 6.0 지진보다 10배 더 강력합니다.그들은 구텐베르크와 함께 지진의 규모와 발생 확률 사이의 확률 분포 관계인 구텐베르크-리히터 법칙을 발견했습니다.그것은 작은 지진이 훨씬 더 자주 일어나고 더 큰 지진은 매우 ^[9]드물게 일어난다고 말합니다.

${{displaystyle N=10^{a-bM}} 표시$

구텐베르크-리히터 법칙은^[10] 비례 상수 밴드 가로채기 a를 사용하여 발생하는 지진의 수 N과 규모 M 사이의 역전력 관계를 보여줍니다.

시뮬레이션

이러한 환경을 진정으로 시뮬레이션하려면 연속적인 무한 3D 시스템이 필요하지만 계산 한계로 인해 2D 셀룰러 오토마타를 사용하여 근사값을 제공할 수 있습니다. 1000x1000 매트릭스 형태의 100만 개의 셀로 대부분의 시나리오를 테스트하기에 충분합니다.각 셀에는 연속적인 양인 셀에 가해지는 힘과 +1(켜짐) 또는 -1(꺼짐)의 정수 값인 셀의 상태라는 두 가지 정보가 저장됩니다.

매개변수화

순력은 균열 소음 시스템의 물리적 특성에 해당할 수 있는 세 가지 구성 요소로 구성됩니다. 첫 번째는 시간(t)에 따라 증가하는 외력장(K)입니다.두 번째 구성 요소는 인접한 셀(S)의 상태 합계에 의존하는 힘이고, 세 번째 구성 요소(r)는 (X)^[11]로 축척된 임의의 구성 요소(r)입니다.

${\displaystyle F_{i}=Kt+\Sigma JS_{i}+Xr_{i}}$

외력 K는 시간(t)으로 곱합니다. 여기서 K는 양의 스칼라 상수이지만, 이는 가변적이거나 음수일 수도 있습니다.S는 셀의 상태(+1 또는 -1)를 나타내며, 두 번째 성분은 네 개의 인접 셀 상태(위, 아래, 왼쪽 및 오른쪽)의 합을 취하여 다른 스칼라 양을 곱합니다. 이는 커플링 상수(J)와 유사합니다.난수 생성기(r)는 평균이 0이고 고정 표준 편차(r_σ)를 갖는 정규 분포 값 범위이며, 이 값에도 스칼라 상수(X)를 곱합니다.순력(F)의 세 가지 구성 요소 중 인접 및 무작위 구성 요소는 양의 값과 음의 값을 생성할 수 있는 반면, 외력은 시간이 지남에 따라 우세한 힘이 되는 시스템에 적용되는 정방향 바이어스가 있다는 것을 의미합니다.

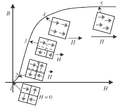
셀의 순력이 양이면 셀을 켜고(+1) 셀의 힘이 음이면 (-1) 꺼집니다.2D 시스템에서는 여러 가지 상태 조합과 배열이 가능하지만, 이는 세 영역, 즉 모든 +1 또는 -1의 두 전역 안정 상태와 두 상태가 혼합된 불안정한 상태로 그룹화될 수 있습니다.전통적으로 시스템이 불안정하면 곧 글로벌 상태 중 하나로 전환되지만, 완벽한 조건, 즉 임계점에서 순력 매개 변수가 균형을 이룰 경우에만 지속 가능한 두 글로벌 상태 사이에 준안정 상태가 형성될 수 있습니다.행렬의 경계 조건은 위에서 아래로, 왼쪽에서 오른쪽으로 감싸며, 코너 셀의 문제는 큰 행렬을 사용하여 부정할 수 있습니다.

탁탁, 탁탁, 탁탁

시스템이 자극에 언제 어떻게 반응하는지 설명하기 위해 세 가지 진술이 형성될 수 있습니다.외부 필드와 다른 구성 요소 간의 차이에 따라 시스템이 팝 또는 크래킹되는지 여부가 결정되지만 랜덤 및 인접 구성 요소의 계수가 외부 필드보다 훨씬 큰 경우 시스템이 0의 밀도로 스냅된 다음 변환 속도를 느리게 하는 특별한 경우도 있습니다.

$display{stylebegin{aligned}Kt<{}&X2r_{\sigma}-\SigmaJS \Rightarrow{text{pping}\Kt>{}&X2r_{\sigmaJS \Rightarrow{text{crackling}-\SigmaJS \Rightarrow{\}에 대한 오른쪽 화살표 텍스트 평형({naping})\R&Rightarrow{{{{{\})}\RigmaJSigmaJSigmaJS}$

팝핑은 시스템에 가역적이고 글로벌 시스템 상태에 무시할 수 있는 영향을 미치는 작은 섭동이 있을 때입니다.

스냅은 큰 셀 클러스터 또는 전체 시스템이 대체 상태, 즉 모든 +1 또는 -1로 전환되는 경우입니다.전체 시스템은 임계점 또는 티핑 지점에 도달한 경우에만 뒤집힙니다.

시스템에서 가역적인 소형 및 대형 클러스터가 펑 하고 끊어지는 현상이 발생할 때 크래킹이 관찰됩니다.시스템은 지속적으로 불균형하고 내부 또는 외부 힘으로 인해 불가능한 평형에 도달하려고 시도합니다.

구성요소의 물리적 의미

랜덤 성분(r)

지진 시뮬레이션을 통해 구텐베르크-리치터 법칙을 관찰할 수 있는데, 이 법칙에서 임의의 성분은 땅과 공기의 임의의 섭동을 나타낼 수 있으며, 이는 격렬한 기상 시스템, 강이 흐르는 것과 같은 자연적인 연속적인 자극, 해안가에 부딪치는 파도 또는 시추와 같은 인간 활동의 어떤 것이든 될 수 있다.이것은 사건의 미래 결과를 예측할 수 없거나 시뮬레이션 중에 설정된 시간에서 원래 상태로 되돌아갈 수 없으며 거시적 수준에서 중요하지 않은 것으로 보이는 나비 효과와 매우 유사합니다.그러나 미시적인 수준에서 사건의 연쇄 반응의 원인이 되었을 수 있습니다. 하나의 셀이 켜지면 전체 시스템이 켜질 수 있습니다.

인접 구성 요소(ΔS)

암석이나 지각판과 같은 물리적 물체에 대한 인접 성분은 뉴턴의 운동 법칙에 대한 설명일 뿐입니다. 만약 판이 움직이고 다른 판과 충돌한다면, 다른 판은 반동력을 제공할 것입니다. 유사하게 많은 느슨한 입자(볼더, 단층)가 이웃에 대해 강제로 작용할 경우,인접한 입자/물체도 이동합니다.

외력(K)

외력은 지각판의 장기적인 움직임 또는 상부 맨틀 내의 액체 암석 전류로, 이는 결국 플레이트가 뒤로 튕기거나 파손되어 시스템에 대한 스트레스를 완화시켜 지진과 같은 안정적인 상태로 뒤집습니다.화산은 지하의 마그마 압력의 축적이 결국 분출을 일으키는 꼭대기의 건조한 바위 층을 극복한다는 점에서 비슷합니다.이러한 모델은 활성 지역에서 지진과 화산의 발생을 예측하고 대규모 사건 후 일반적인 여진을 예측하는 데 사용될 수 있습니다.

실용적 응용 프로그램

자석이 자화되는 동안, 외부 필드는 인가된 전기장이고, 인접 구성 요소는 쌍극자의 국부적 자기장의 영향이며, 무작위 구성 요소는 외부 또는 내부 자극의 다른 섭동을 나타냅니다.이에 대한 실용적인 응용 분야는 여러 가지가 있으며, 제조업체는 이러한 유형의 시뮬레이션을 사용하여 특정 조건에서 자석이 어떻게 반응하는지를 비파괴적으로 테스트할 수 있습니다.큰 힘(예: 해머 블로우)을 취하거나 바닥에 떨어뜨린 후 자화를 테스트하기 위해 외력(H) 또는 커플링 상수(J)를 갑자기 증가시킬 수 있습니다.열 조건을 테스트하려면 열 변동(X 증가)이 증가하는 한 에지에 경계 조건을 적용할 수 있으며, 이를 위해서는 3차원 모델이 필요합니다.

비즈니스 세계

주가의 행동은 보편성의 특성을 보여주었습니다.회사의 ^[12]과거 주가 데이터를 가져옴으로써 일일 수익률을 계산한 다음 이를 히스토그램에 표시하면 뚱뚱한 꼬리의 비가우스 분포가 생성됩니다.주가는 작은 변동과 함께 끊임없이 변동할 것이고 더 큰 변동은 훨씬 더 드물 것입니다. 증권 거래소는 공급과 수요 할당량에 가격을 조정하여 주가를 균형 있게 만들 책임이 있는 힘으로 해석될 수 있습니다.

작은 회사들이 정기적으로 형성되는, 종종 매우 변동성이 큰 신생 기업들의 합병은, 만약 그것이 일정 기간 동안 지속된다면, 그것은 계속 성장할 가능성이 높고, 일단 충분히 커지면, 그것은 자신의 규모를 증가시키는 다른 작은 회사들을 살 수 있습니다.이는 시장이 포화 상태가 될 때까지 시장 점유율을 높이기 위해 경쟁업체를 매수하는 것과 같습니다.

자연계의 예

시스템 상태에 기여하는 외부 요인이 너무 많기 때문에 실제 세계의 시스템이 영구적인 평형 상태를 유지하는 것은 불가능합니다.시스템은 일시적인 평형 상태에 있다가 자극으로 인해 갑자기 고장이 나거나 시스템의 균형을 맞추려는 외부 힘으로 인해 위상이 지속적으로 변화하는 상태에 있을 수 있습니다.이러한 시스템은 펑, 스니핑 및 크래킹 동작을 관찰합니다.

• 

  종이가 구겨지면 ^[2]탁탁 소리가 납니다.

• 

  지진 규모의 함수로서 지진의 빈도(Gutenberg-Richter law).

• 

  강자성 막대의 영역이 외부 자기장에 정렬되는 속도는 바크하우젠 효과를 생성합니다.

• 

  옥수수가 터지는 소리는 ^[5]탁탁 소리가 아니라 탁탁 터지는 소리입니다.

• 

  과도한 눈 축적으로 인한 눈사태의 크기 분포는 몇 가지 ^[13]규모에 걸쳐 있습니다.

• 

  나무의 비탄성 기계적 특성으로 인해 연필이 부러지는 현상은 ^[5]탁탁 소리가 아니라 탁탁 소리가 나는 경우입니다.

• 

  산사태의 분포는 두더지 붕괴에서 산허리 붕괴에 이르기까지 탁탁거리는 소음입니다.

• 

  화산은 내부 마그마 흐름의 압력 축적이 바다표범보다 클 때 결국 폭발할 것입니다.

• 

  Van der Waals 힘은 물 표면에 형성되는 지방 구형이 서로 끌어당겨 자유 에너지를 줄이고 더 큰 클러스터가 된다는 것을 의미합니다.

• 

  뻥튀기는 우유를 넣으면 바삭바삭 소리가 납니다.

레퍼런스