4 21 폴리토프
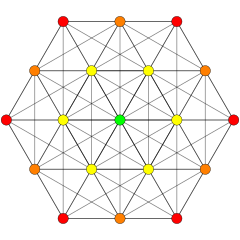
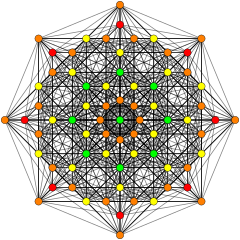
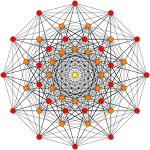
4 21 polytope| E6 Coxeter 평면의 직교 투영 | ||
|---|---|---|
 421 | 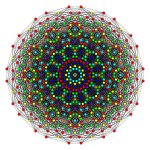 142 |  241 |
 수정4길21 |  수정42 1 |  수정2길41 |
 양방향21 4 |  삼보정4길21 | |
8차원 기하학에서 4는21 반정형 8폴리토프(Semiplular confirm 8-polytope)로 E그룹의8 대칭성 내에서 구성된다. 그것은 그의 1900년 논문에 발표된 소럴드 고셋에 의해 발견되었다. 그는 그것을 8ic 반정규격이라고 불렀다.[1]
그것의 Coxeter 심볼은 4로21, 그것의 분리되는 Coxeter-Dynkin 도표를 묘사하고 있고, 4-노드 시퀀스 끝에 하나의 링이 있다.
정류된 4는21 4의21 중간 부분에 있는 점으로 구성된다. 양방향 4는21 4의21 삼각형 면 중심에 있는 점에 의해 구성된다. 3차 수정 4는21 4의21 사면 중심에 있는 점으로 구성된다.
이러한 폴리토프는 255 = 28 - 1 볼록 균일 8 폴리토프 계열의 일부로서, 이 Coxeter-Dynkin 다이어그램에서 하나 이상의 고리의 모든 순열에 의해 정의된 균일한 7 폴리토프 면과 정점 수치로 만들어졌다.
421 폴리토프
| 421 | |
|---|---|
| 유형 | 제복8폴리토프 |
| 가족 | k21 폴리토프 |
| 슐레플리 기호 | {3,3,3,3,32,1} |
| 콕시터 기호 | 421 |
| 콕시터 도표 | = |
| 7시 15분 | 총 19440: 2160 411 17280 {36} |
| 6시 15분 | 207360: 138240 {35} 69120 {35} |
| 5시 15분 | 483840 {34} |
| 4시 15분 | 483840 {33} |
| 세포 | 241920 {3,3} |
| 얼굴 | 60480 {3} |
| 가장자리 | 6720 |
| 정점 | 240 |
| 정점수 | 321 폴리토프 |
| 페트리 폴리곤 | 30곤 |
| 콕시터군 | E8, [34,2,1], 696729600 주문 |
| 특성. | 볼록하게 하다 |
4개의21 폴리토프는 17,280개의 7-심플렉스, 2,160개의 7-정형 면과 240개의 정점을 가지고 있다. 그것의 꼭지점은 3개의21 폴리토프다. 그것의 꼭지점은 단순한 Lie 그룹 E의8 루트 벡터를 나타내기 때문에, 이 폴리토프를 E 루트8 폴리토프라고 부르기도 한다.
이 폴리토프의 정점은 또한 규범 1의 240 통합 옥톤을 취함으로써 얻을 수 있다. 팔괘는 연관성이 없는 규범적인 분할 대수이기 때문에 이 240점에는 곱셈 연산이 있어 집단이 아니라 오히려 루프, 사실상 무방 루프(Moufang Loop)가 된다.
시각화를 위해 이 8차원 폴리토프는 종종 일반 3차원 입체각형(Petrie polygon이라 불림) 내에서 240 정점에 맞는 특별한 비스듬한 정사각형 투영 방향으로 표시된다. 그것의 6720개의 가장자리는 240개의 꼭지점 사이에 그려져 있다. 특정 상위 요소(페이스, 셀 등)도 이 투영에 추출하여 그릴 수 있다.
대체 이름
- 이 폴리토프는 소럴드 고셋에 의해 발견되었는데, 그는 1900년 논문에서 이를 8ic 반정규격으로 묘사했다.[1] 그것은 그의 열거에 있어서 마지막의 유한한 반정형이며, 그에게 있어 반정형적인 모습은 그것이 규칙적인 면만을 포함하고 있다는 것을 의미한다.
- E. L. Elte는 그의 1912년 반정형 폴리토페스 리스트에서 그것을240 V(정점 240을 위해)라고 명명했다.[2]
- H.S.M. Coxeter는 그것의 Coxeter-Dynkin 도표에는 길이 4, 2, 1의 세 가지 가지가 있고, 4개의 분기의 터미널 노드에 하나의 노드가 있기 때문에 그것을21 4라고 불렀다.
- Dischiliahectohexaconta-myriaheptachiaciacoxaconta-zetton (Acronim Fyy) - 2160-17280 faceted polyzetton (Jonathan Bowers)[3]
좌표
그것은 와이토프 건설에 의해 8차원 공간에 있는 8개의 하이퍼플레인 미러 세트에 의해 만들어졌다.
는 421다면체의 240vertices 좌표(±에서 수집된 정보와 좌표(±2±2,0,0,0,0,0,0){\displaystyle(\pm 2,\pm 2,0,0,0,0,0,0)\,}에서 징후는 임의의 조합을 통해 얻은과 좌표는 임의의 조합 및 128뿌리(27)로 두:112(22×8C2)으로 구성될 수 있다.1,±,± ,± 1,± , ± ± 1 ± )(\ 1 1 1 1pm 1,\ 1 1,\ 1 1을(또는 동등하게, 모든 8개 좌표의 합이 4의 배수여야 함).
Each vertex has 56 nearest neighbors; for example, the nearest neighbors of the vertex are those whose coordinates sum to 4, namely the 28 obtained by permuting the coordinates of and the 28 obta,,1, ,,1, ,1, , 1,-,- 1 )의 좌표를 허용하여 삽입한다 {\11,1,1,-1)의 좌표. 이 56점은 7차원의 3 폴리토프의21 정점이다.
Each vertex has 126 second nearest neighbors: for example, the nearest neighbors of the vertex are those whose coordinates sum to 0, namely the 56 obtained by permuting the coordinates of and ,,1, ,1, ,- , -, - 1,- )의 좌표를 허용하여 얻은 70개 (1, 1,-의 좌표 이 126점은 7차원의 2개의31 폴리토프의 정점이다.
또한 각 꼭지점에는 가장 가까운 이웃의 부정적인 면인 56번째 가장 가까운 이웃이 있으며, 의 반정점이 있으며, 총 1 ++ + 1= 정점이다.
또 다른 분해는 확장된 8-심플렉스로서 9-dimension으로 240점을 주고, 반대편인 2-심플렉스 8-심플렉스 및 .
- (3,-3,0,0,0,0,0,0,0) : 72정점
- (-2,-2,-2,-1,1,1,1) : 84정점
- (2,2,2,-1,-1,-1,-1,-1,-1) : 84정점
이는 A8 미러 8개를 공유하는 A8 격자와 E8 격자의 관계와 유사하게 발생한다.
| 이름 | 421 | 8배수 확장형 | 양방향으로 된 8배수 | 양방향으로 된 8배수 |
|---|---|---|---|---|
| 정점 | 240 | 72 | 84 | 84 |
| 이미지 |  |  |  | |
테셀레이션스
이 폴리토프는 기호 5와21 Coxeter-Dynkin 도표로 표현되는 8차원 공간의 균일한 다듬기를 위한 꼭지점 그림이다.
시공 및 면
이 폴리토프의 면 정보는 Coxeter-Dynkin 도표에서 추출할 수 있다.
짧은 가지에서 노드를 제거하면 7-단순함:
2-길이 가지 끝에 있는 노드를 제거하면 7-정맥이 교체된 형태(411):
매 7단계의 정면은 7단계의 면만 만지는 반면, 직각의 면은 단순 또는 다른 직각의 면만 만지는 것이다. 단순 면은 17,280개, 직교 면은 2160개가 있다.
매 7-심플렉스에는 각각 다른 6-심플렉스 면이 7개씩 있기 때문에 4개의21 폴리토프에는 7-심플렉스 면인 12만960개(7×17,280개)의 6-심플렉스 면이 있다. 모든 7정맥은 128(27) 6심플렉스 면을 가지며, 그 중 절반은 7심플렉스 면에 해당되지 않기 때문에 4개의21 폴리토프는 13만8,240(26×2160) 6심플렉스 면으로 7심플렉스 면이 아니다. 따라서 4개의21 폴리토프는 이 폴리토프의 대칭에 의해 상호 교환되지 않고 두 종류의 6-단순 표면을 가지고 있다. 6-심플렉스 면의 총수는 259200(120,960+138,240)이다.
단일 링 폴리토프의 꼭지점은 링된 노드를 제거하고 인접 노드를 울림으로써 얻는다. 이것은 3개의21 폴리토프를 만든다.
구성 매트릭스에서 볼 수 있는 요소 카운트는 미러 제거 및 Coxeter 그룹 주문 비율에 의해 도출될 수 있다.[4]
| E8 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | 크-피규격 | 메모들 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E7 | ( ) | f0 | 240 | 56 | 756 | 4032 | 10080 | 12096 | 4032 | 2016 | 576 | 126 | 3_21 폴리토프 | E8/E7 = 192×10!/(72×8!) = 240 | |
| A1E6 | { } | f1 | 2 | 6720 | 27 | 216 | 720 | 1080 | 432 | 216 | 72 | 27 | 2_21 폴리토프 | E8/A1E6 = 192×10!/(2×72×6!) = 6720 | |
| A2D5 | {3} | f2 | 3 | 3 | 60480 | 16 | 80 | 160 | 80 | 40 | 16 | 10 | 5데미큐브 | E8/A2D5 = 192×10!/(6×24×5!) = 60480 | |
| A3A4 | {3,3} | f3 | 4 | 6 | 4 | 241920 | 10 | 30 | 20 | 10 | 5 | 5 | 수정 5-셀 | E8/A3A4 = 192×10!/(4!×5!) = 241920 | |
| A4A2A1 | {3,3,3} | f4 | 5 | 10 | 10 | 5 | 483840 | 6 | 6 | 3 | 2 | 3 | 삼각 프리즘 | E8/AAA421 = 192×10!/(5!×3)!×2) = 483840 | |
| A5A1 | {3,3,3,3} | f5 | 6 | 15 | 20 | 15 | 6 | 483840 | 2 | 1 | 1 | 2 | 등각 삼각형 | E8/A5A1 = 192×10!/(6!×2) = 483840 | |
| A을6 | {3,3,3,3,3} | f6 | 7 | 21 | 35 | 35 | 21 | 7 | 138240 | * | 1 | 1 | { } | E8/A6 = 192×(10!×7!) = 138240 | |
| A6A1 | 7 | 21 | 35 | 35 | 21 | 7 | * | 69120 | 0 | 2 | E8/A6A1 = 192×10!/(7!×2) = 69120 | ||||
| A을7 | {3,3,3,3,3,3} | f7 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 0 | 17280 | * | ( ) | E8/A7 = 192×10!/8! = 17280 | |
| D7 | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 64 | 64 | * | 2160 | E8/D7 = 192×10!/(26×7!) = 2160 | |||
투영
 스트링 아트로 만든 4개의21 그래프. | 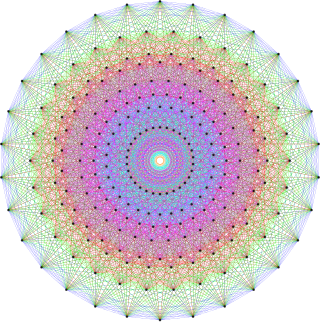 E8 Coxeter 평면 투영 |
3D
 E8에 대한 물리적 Zome 모델의 수학적 표현. 이것은 2개의 동심 600 셀(황금비)에서 길이 √2(√5-1)의 3360 가장자리를 모두 가진 VisibLie_E8 그림에서 직교 투영과 투시 3-공간으로 구성된다. | 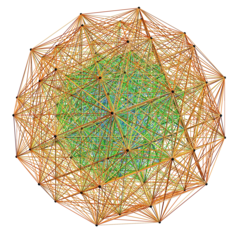 실제 분할 실제 E8 4 폴리토프는21 길이 6720의 모든 가장자리를 가진 투시 3-공간으로 투영된다2[5] |  E8은 H4+H4φ로 회전하여 3D로 투사하여 STL로 변환하고 나일론 플라스틱으로 인쇄하였다. 사용된 투영 기준: E8은 H4+H4φ로 회전하여 3D로 투사하여 STL로 변환하고 나일론 플라스틱으로 인쇄하였다. 사용된 투영 기준:
|
2D
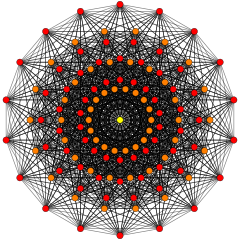
이 그래프는 E8, E7, E 및6 B8, D, D87, D65, D4, D, D3, D7, A5, Coxeter 평면에서 정자 투영을 나타낸다. 정점 색상은 투영에서 겹치는 곱셈에 의해, 즉 빨강, 주황, 노랑, 초록과 같은 곱의 순서를 증가시켜 색칠된다.
k가족21
4개의2121 폴리토프는 k 폴리토페즈라고 불리는 가족에서 마지막이다. 이 계열의 첫 번째 폴리토프는 세 개의 사각형(2정형)과 두 개의 삼각형(2심형)으로 구성된 반정형 삼각 프리즘이다.
기하학적 폴딩
4는21 콕시터-딘킨 도표의 기하학적 접힘에 의한 600셀과 관련이 있다. 이는 E8/H4 Coxeter 평면 투영에서 확인할 수 있다. 4개의21 폴리토프의 240개의 꼭지점은 같은 방향의 다른 쪽보다 작은 1개의 복사본(황금 비율에 따라 크기 조정)인 600셀의 120 꼭지점 중 2개의 복사본으로 4-공간으로 투영된다. E8/H4 Coxeter 평면에서 2D 직교 투영으로 보여지는 600 셀의 120 정점은 4에서21 보는 것과 동일한 4개의 링에 투영된다. 4개의21 그래프의 나머지 4개의 링도 600개의 링의 작은 복사본과 일치한다.
| E8/H4 콕시터 평면 접힘 | |
|---|---|
| E8 | H4 |
 421 |  600셀 |
| [20] 대칭 평면 | |
 421 | 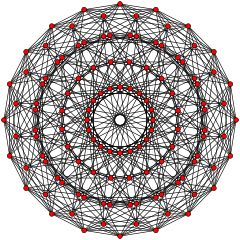 600셀 |
관련 폴리토페스
4차원 복합 기하학에서는 일반 복합 폴리토프 {3}{33}{33}{3}},3 Coxeter 다이어그램이 421 폴리토프와 동일한 정점 배열을 가지고 존재한다. 그것은 자업자득이다. 콕세터는 알렉산더 위팅의 이름을 따서 그것을 위팅 폴리토프라고 불렀다. Coxeter는 쉐퍼드 그룹의 대칭을 [3][33][33][3][3]로 표현한다.3[7]
4는21 반정형 폴리토페스의 치수 시리즈 중 6번째다. 각 진행성 균일 폴리토프는 이전 폴리토프의 꼭지점 형상으로 구성된다. 소럴드 고셋은 1900년에 이 시리즈가 모든 단순함과 직교로 구성된 모든 규칙적인 폴리토프 면을 포함하고 있다고 밝혔다.
| n차원의21 k자 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 공간 | 유한한 | 유클리드 주 | 쌍곡선 | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 콕시터 무리를 짓다 | E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E98+ = ~ = E | E10 = 8++ = E | |||
| 콕시터 도표를 만들다 | |||||||||||
| 대칭 | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| 주문 | 12 | 120 | 1,920 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
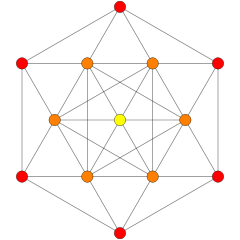
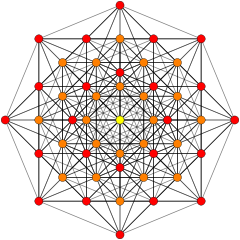
| 그래프 |  |  |  |  |  |  | - | - | |||
| 이름 | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
수정 4_21 폴리토프
| 수정4길21 | |
|---|---|
| 유형 | 제복8폴리토프 |
| 슐레플리 기호 | t1{3,3,3,32,1} |
| 콕시터 기호 | t1(421) |
| 콕시터 다이어그램 | |
| 7시 15분 | 총 19680개: |
| 6시 15분 | 375840 |
| 5시 15분 | 1935360 |
| 4시 15분 | 3386880 |
| 세포 | 2661120 |
| 얼굴 | 1028160 |
| 가장자리 | 181440 |
| 정점 | 6720 |
| 정점수 | 221 프리즘 |
| 콕시터군 | E8, [34,2,1] |
| 특성. | 볼록하게 하다 |
정류된 4는21 4개의21 폴리토프를 정류하여 4개의21 가장자리 중심에 새로운 정점을 만드는 것으로 볼 수 있다.
대체 이름
- 2160-17280 폴리제톤(Acronym riffy)(Jonathan Bowers)[8]을 수정하기 위한 dischiliahectohexaconta-myriaheptachiacoxacconta-zetton(조나단 보우어즈)
건설
그것은 와이토프 건설에 의해 8차원 공간에 있는 8개의 하이퍼플레인 미러 세트에 의해 만들어졌다. 그것은 4를21 바로 잡는 것으로 이름 지어졌다. 정점은 4의21 모든 가장자리와 이들을 연결하는 새로운 가장자리의 중간점에 위치한다.
면 정보는 Coxeter-Dynkin 도표에서 추출할 수 있다.
짧은 가지에서 노드를 제거하면 7단계가 수정된다.
2-길이 분기 끝에 있는 노드를 제거하면 정류된 7-정맥이 교체된 형태로 남게 된다.
4-길이 분기 끝에 있는 노드를 제거하면 321:
꼭지점 수치는 링 노드를 제거하고 인접 노드에 링을 추가함으로써 결정된다. 이것은21 2 프리즘을 만든다.
좌표
정류된 4의21 6720 꼭지점의 데카르트 좌표는 세 개의 다른 균일한 폴리토프로부터의 좌표의 모든 순열에 의해 주어진다.
- 난독성 8자리 - 홀수 음수: ½(±1,±1,±1,±1,±1,±1,±3) - 3584 정점[9]
- 양방향 8자리 - (0,0,±1,±1,±1,±1) - 1792 정점[10]
- 알 수 있는 8정맥 - (0,0,0,0,0,0,0,0,±1,±2) - 1344정점[11]
| 이름 | 수정4길21 | 양방향 8로 된 | 난독성 8인치 | 8인칭 |
|---|---|---|---|---|
| 정점 | 6720 | 1792 | 3584 | 1344 |
| 이미지 |  | 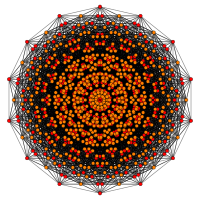 |  |  |
투영
2D
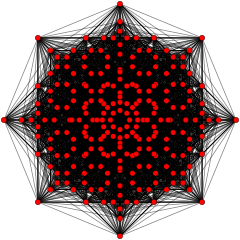
이 그래프는 E8, E7, E 및6 B8, D, D87, D65, D4, D, D3, D7, A5, Coxeter 평면에서 정자 투영을 나타낸다. 정점 색상은 투영에서 겹치는 곱셈에 의해, 즉 빨강, 주황, 노랑, 초록과 같은 곱의 순서를 증가시켜 색칠된다.
| 직교 투영 | ||
|---|---|---|
| E8 / H4 [30] | [20] | [24] |
 | 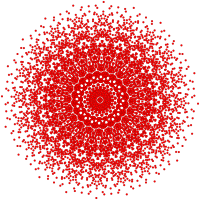 |  |
| E7 [18] | E6 / F4 [12] | [6] |
 |  |  |
| D3 / B2 / A3 [4] | D4 / B3 / A2 / G2 [6] | D5 / B4 [8] |
 |  |  |
| D6 / B5 / A4 [10] | D7 / B6 [12] | D8 / B7 / A6 [14] |
 | 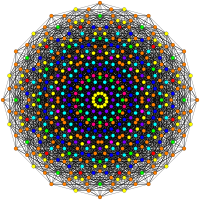 |  |
| B8 [16/2] | A을5 [6] | A을7 [8] |
 | 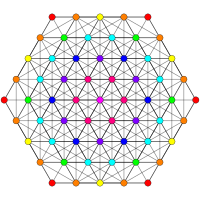 |  |
양방향 4_21 폴리토프
| 양방향21 4폴리토프 | |
|---|---|
| 유형 | 제복8폴리토프 |
| 슐레플리 기호 | t2{3,3,3,32,1} |
| 콕시터 기호 | t2(421) |
| 콕시터 다이어그램 | |
| 7시 15분 | 총 19680개: |
| 6시 15분 | 382560 |
| 5시 15분 | 2600640 |
| 4시 15분 | 7741440 |
| 세포 | 9918720 |
| 얼굴 | 5806080 |
| 가장자리 | 1451520 |
| 정점 | 60480 |
| 정점수 | 5데미큐브식 듀오프리즘 |
| 콕시터군 | E8, [34,2,1] |
| 특성. | 볼록하게 하다 |
양방향 4는21 균일한 421 폴리토프의 두 번째 정류로 볼 수 있다. 이 폴리토프의 정점은 4의21 모든 60480 삼각형 면의 중심에 위치한다.
대체 이름
- 양방향 2160-17280 폴리제톤(아크로니마 붕소)을 위한 양방향 이실리아헥사콘타-미리아헥사콘타-제톤(Jonathan Bowers)[12]
건설
그것은 와이토프 건설에 의해 8차원 공간에 있는 8개의 하이퍼플레인 미러 세트에 의해 만들어졌다. 그것은 4를21 양방향으로 하는 것으로 이름이 지어졌다. 정점은 4의21 모든 삼각형 면의 중심에 위치한다.
면 정보는 Coxeter-Dynkin 도표에서 추출할 수 있다.
짧은 가지에서 노드를 제거하면 양방향 7-단순함이 남는다. 이런 면은 17280개가 있다.
2길이 가지 끝에 있는 노드를 제거하면 양방향 7정맥이 번갈아 나타난다. 이런 면은 2160개가 있다.
4-길이 분기 끝에 있는 노드를 제거하면 수정된 3이21 남는다. 이런 면은 240개가 있다.
꼭지점 수치는 링 노드를 제거하고 인접 노드에 링을 추가함으로써 결정된다. 이것은 5데미큐브-삼각형 듀오프리즘을 만든다.
투영
2D
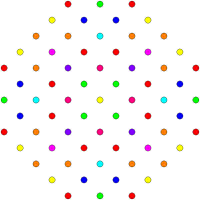
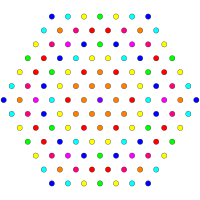
이 그래프는 E8, E7, E 및6 B8, D, D87, D65, D4, D, D3, D7, A5, Coxeter 평면에서 정자 투영을 나타낸다. 가장자리가 그려지지 않는다. 정점 색상은 투영에서 겹치는 승수(빨간색, 주황색, 노란색, 녹색 등)에 의해 색상이 지정된다.
| 직교 투영 | ||
|---|---|---|
| E8 / H4 [30] | [20] | [24] |
 |  |  |
| E7 [18] | E6 / F4 [12] | [6] |
 |  |  |
| D3 / B2 / A3 [4] | D4 / B3 / A2 / G2 [6] | D5 / B4 [8] |
 |  |  |
| D6 / B5 / A4 [10] | D7 / B6 [12] | D8 / B7 / A6 [14] |
 |  |  |
| B8 [16/2] | A을5 [6] | A을7 [8] |
 |  |  |
3차 수정 4_21 폴리토프
| 3정형21 4폴리토프 | |
|---|---|
| 유형 | 제복8폴리토프 |
| 슐레플리 기호 | t3{3,3,3,32,1} |
| 콕시터 기호 | t3(421) |
| 콕시터 다이어그램 | |
| 7시 15분 | 19680 |
| 6시 15분 | 382560 |
| 5시 15분 | 2661120 |
| 4시 15분 | 9313920 |
| 세포 | 16934400 |
| 얼굴 | 14515200 |
| 가장자리 | 4838400 |
| 정점 | 241920 |
| 정점수 | 사면 수정 5세포 듀오프리즘 |
| 콕시터군 | E8, [34,2,1] |
| 특성. | 볼록하게 하다 |
대체 이름
- 3차 수정 2160-17280 폴리제톤(아크로니엄 토피)을 위한 3차 수정 디스칠리아헥사콘타-마이리아헥사콘타-마이리아헥사콘타-제트톤(Jonathan Bowers)[13]
건설
그것은 와이토프 건설에 의해 8차원 공간에 있는 8개의 하이퍼플레인 미러 세트에 의해 만들어졌다. 그것은 4를21 양방향으로 하는 것으로 이름이 지어졌다. 정점은 4의21 모든 삼각형 면의 중심에 위치한다.
면 정보는 Coxeter-Dynkin 도표에서 추출할 수 있다.
짧은 가지에서 노드를 제거하면 3중으로 수정된 7-단순함:
2-길이 가지 끝에 있는 노드를 제거하면 3-정직된 7-정직자가 대체된 형태로 남는다.
4-길이 분기 끝에서 노드를 제거하면 양방향으로 설정된 3이21 남는다.
꼭지점 수치는 링된 노드를 제거하고 인접 노드를 링하여 결정한다. 이것은 4면체 수정 5세포 듀오프리즘을 만든다.
투영
2D
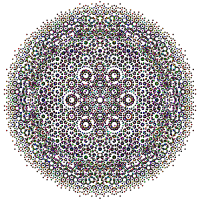
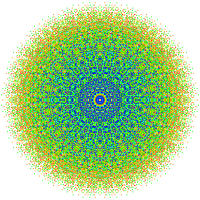
이 그래프는 E7, E6, B8, D8, D, D765, D, D4, D, D3, D, A 및7 A5 Coxeter 평면의 직교 투영을 나타낸다. 정점 색상은 투영에서 겹치는 곱셈에 의해, 즉 빨강, 주황, 노랑, 초록과 같은 곱의 순서를 증가시켜 색칠된다.
(E와8 B가8 너무 커서 표시할 수 없음)
| 직교 투영 | ||
|---|---|---|
| E7 [18] | E6 / F4 [12] | D4 - E6 [6] |
 |  |  |
| D3 / B2 / A3 [4] | D4 / B3 / A2 / G2 [6] | D5 / B4 [8] |
 |  |  |
| D6 / B5 / A4 [10] | D7 / B6 [12] | D8 / B7 / A6 [14] |
 |  | |
| A을5 [6] | A을7 [8] | |
 |  | |
참고 항목
메모들
- ^ a b 고셋, 1900년
- ^ 1912년 엘테
- ^ 클라이칭, (o3o3o3o *c3o3o3o3x - fy)
- ^ 콕시터, 일반 폴리토페스, 11.8 고셋은 6차원, 7차원, 8차원, 202-203페이지.
- ^ e8Flyer.nb
- ^ 데이비드 리히터: 고셋의 8차원 형상, 조메 모델
- ^ Coxeter 정규 볼록 폴리토페스, 12.5 Witting 폴리토페
- ^ 클라이칭, (o3o3o3o *c3o3o3x3o - 리피)
- ^ https://bendwavy.org/klitzing/incmats/sotho.htm
- ^ https://bendwavy.org/klitzing/incmats/bro.htm
- ^ https://bendwavy.org/klitzing/incmats/srek.htm
- ^ 클라이칭, (o3o3o3o *c3o3x3o3o - 보르피)
- ^ 클라이칭, (o3o3o3o *c3x3o3o3o - 토피)
참조
- T. 고셋: 수학의 메신저 맥밀런, 1900년 n차원의 정규 및 반정규격 수치에 관한 연구, 1900년
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- Coxeter, H. S. M, 정규 복합 폴리토페스, 캠브리지 대학 출판부 (1974)
- 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글. 아서 셔크, 피터 맥멀런, 앤서니 C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[1]
- (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술] Zeit. 200 (1988) 3-45] Peter McMullen의 p347 (그림 3.8c) 참조: (30-곤 노드-엣지 그래프 421)
- Klitzing, Richard. "8D uniform polytopes (polyzetta)". o3o3o3o3o3o3x - fy, o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o3o - torfy - torfyfy
| 가족 | A을n | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 다각형 | 삼각형 | 사각형 | p-곤 | 육각형 | 펜타곤 | |||||||
| 균일다면체 | 사면체 | 옥타헤드론 • 큐브 | 데미큐브 | 도데카헤드론 • 이코사헤드론 | ||||||||
| 균일 폴리초론 | 펜타코론 | 16-셀 • 테세락트 | 데미테세락트 | 24셀 | 120 셀 • 600 셀 | |||||||
| 제복5폴리토프 | 5와섹스 | 5정형 • 5정형 | 5데미큐브 | |||||||||
| 제복6폴리토프 | 6-630x | 6-정통 • 6-118 | 6데미큐브 | 122 • 221 | ||||||||
| 제복7폴리토프 | 7시 15분 | 7정맥 • 7정맥 | 7데미큐브 | 132 • 231 • 321 | ||||||||
| 제복8폴리토프 | 8시 15분 | 8정형 • 8정형 | 8데미큐브 | 142 • 241 • 421 | ||||||||
| 제복9폴리토프 | 9시 15분 | 9-정통 • 9-11 | 9데미큐브 | |||||||||
| 균일 10폴리토프 | 10센트짜리 | 10정형 • 10정형 | 10데미큐브 | |||||||||
| 균일 n폴리토프 | n-제곱스 | n-직관 • n-직관 | n-데미큐브 | 1k2 • 2k1 • k21 | n-자갈 폴리토프 | |||||||
| 주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록 | ||||||||||||
 (또는 동등하게, 모든 8개 좌표의 합이 4의 배수여야 함).
(또는 동등하게, 모든 8개 좌표의 합이 4의 배수여야 함).