택시캡 기하학

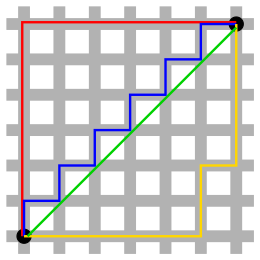
택시카브 기하학 또는 맨해튼 기하학은 익숙한 유클리드 거리가 무시되는 기하학이며, 대신 두 점 사이의 거리는 택시카브 거리, 맨해튼 거리 또는 도시 블록 거리라고 불리는 거리 함수(또는 미터법)인 각각의 데카르트 좌표의 절대 차이의 합으로 정의됩니다. 이 이름은 맨해튼 섬, 또는 일반적으로 택시가 격자 방향으로만 이동할 수 있는 직사각형 모양의 거리가 있는 계획된 도시를 말합니다. 택시캡 기하학에서 두 점 사이의 거리는 가장 짧은 격자 경로의 길이와 같습니다. 거리에 대한 이러한 다른 정의는 곡선의 길이에 대한 다른 정의로 이어지는데, 두 점 사이의 선분은 유클리드 길이가 아니라 두 점 사이의 격자 경로와 동일한 길이를 갖습니다.

택시 택시 거리는 직선 거리 또는 L¹ 거리라고도 합니다(L^p 공간 참조).^[1] 이 기하학은 18세기부터 회귀 분석에 사용되었으며, 흔히 LASSO라고 합니다. 그것의 기하학적 해석은 19세기의 비유클리드 기하학으로 거슬러 올라가며 헤르만 민코프스키에 의한 것입니다.

2차원 실수 좌표 공간${\displaystyle {}^{}}$에서 ${\displaystyle \mathbb {R}^{2}}$ 두$$ 점${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ y ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle (x_{1},$ ${\displaystyle {y\_\mathrm{}}_{}}$${1})}$ 및$$${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ 2${\displaystyle {}_{}}$ ${\displaystyle (x_{2})$$y_{2}}$는 ${\displaystyle x{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$- ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}}$+ ${\displaystyle {y\mathrm{}}_{}}$ ${\displaystyle 1{}_{}}$- ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ $displaystyle \left x_{1}-x_{2}\right +\left y_{1}-y_{2}\right$입니다$.$ 즉, 두 좌표의 차이의 절대값의 합입니다.

형식적 정의

${\displaystyle {택시}_{}}$ 택시 거리 $d{\displaystyle {}_{}}$ T ${\$$T$$\}\},$ 고정 직교 좌표계를 갖는 n차원 실수 좌표계 공간에서 두 점 p $=$ ${\displaystyle ({}_{}}$1${\displaystyle {}_{}}$ p $2,$ …, p n) 및 q $=$ (q 1, q 2, …, q n) {\displaystyle \mathbf {p} $=$ (p_{1}, p_{2},\ $dots$,p_{n}){\text{ 및 }}\mathbf {q} $=$ (q_{1}, q_{2},\ $dots$, q_{n})} 좌표 축에 점 사이의 선분 투영 길이의 합입니다. 좀 더 형식적으로,

For example, in ${\displaystyle \mathbb {R} ^{2}}$, the taxicab distance between ${\displaystyle \mathbf {p} =(p_{1},p_{2})}$ and ${\displaystyle \mathbf {q} =(q_{1},q_{2})}$ is ${\displaystyle p_1-q_1+p_2-q_2.}$${\displaystyle \left p_{1}-q_{1}\right +\left p_{2}-q_{2}\right.}$

역사

L¹ 메트릭은 1757년 Roger Joseph Boscovich에 의해 적합도의 척도로 회귀 분석에 사용되었습니다.^[2] 기하학적 공간에서 점 사이의 거리로 해석하는 것은 19세기 후반과 비유클리드 기하학의 발전으로 거슬러 올라갑니다. 특히 1910년에 프리게스 리에즈와 헤르만 민코프스키의 작품에 등장했습니다. 특수한 경우로 택시캡 기하학을 포함하는 L^p 공간의 형식화는 Riesz에게 인정됩니다.^[3] 헤르만 민코프스키는 수의 기하학을 발전시키면서 이 공간들이 정규화된 벡터 공간을 정의한다고 말하면서 자신의 민코프스키 부등식을 확립했습니다.^[4]

택시캡 기하학이라는 이름은 1952년 칼 멩거(Karl Mengger)가 시카고 과학 산업 박물관(Museum of Science and Industry)에서 열린 일반 대중을 위한 기하학 전시회와 함께 소개한 책자 '기하학을 좋아할 것입니다'에서 소개했습니다.^[5]

특성.

유클리드 공간에 계층화된 추가 구조로 생각되는 택시 캡 거리는 좌표계의 방향에 따라 달라지며 공간의 유클리드 회전에 의해 변경되지만 번역 또는 축 정렬 반사에 의해 영향을 받지 않습니다. 택시카브 기하학은 각도의 합동을 유클리드 개념과 정확히 일치하도록 정의할 수 없고 합동 택시카브 각도의 그럴듯한 정의 아래서 정의할 수 없다는 점을 제외하고는 힐베르트의 모든 공리(유클리드 기하학의 형식화)를 만족합니다. 변-각 변 공리는 일반적인 삼각형과 마찬가지로 만족되지 않으며, 두 개의 택시 결합 변과 그 사이의 택시 결합 각은 결합 삼각형이 아닙니다.

구

임의의 미터법 공간에서 구는 특정 중심점으로부터 일정한 거리, 즉 반지름에 있는 점들의 집합입니다. 유클리드 구는 둥글고 회전 대칭인 반면, 택시카브 거리 아래에서 구의 모양은 교차 폴리토프이며, 일반 팔면체의 n차원 일반화이며, $점{\displaystyle \mathbf{}}$ p ${\$는 다음 방정식을 만족합니다$$.

${\displaystyle d_{\text}T}}(\mathbf {p} ,\mathbf {c} )=\sum _{i=1}^{n} p_{i}-c_{i} =r,}$

여기서 $c{\displaystyle \mathbf{}}$ ${\$는 중심이고 r은 반지름입니다. $원점$을 중심으로 하는 반지름 1의 구인 단위 구 위의 점 $p$ ${\displaystyle \mathbf${$\mathrm{p}$$}$= 방정식 $d_{}$ $T{}_{}$($p,$ $\underset{}{\overset{}{0}})$ = ∑ $i_{}\underset{}{\overset{}{}}$= 1 n$$pi = 1. {\$textstyle$d_{\text}$T}}(\mathbf {p} ,\mathbf {0} )=\sum _{i=1}^{n} p_{i} =1.}$

2차원 택시 기하학에서 구(원이라고 함)는 좌표 축에 대해 대각선으로 배향된 정사각형입니다. 오른쪽 이미지는 파란색 중앙에서 고정된 거리를 가진 정사각형 그리드의 모든 점 집합을 빨간색으로 표시합니다. 그리드가 미세하게 만들어지면 빨간색 점이 더 많아지고 한계에서는 연속적으로 기울어진 사각형이 되는 경향이 있습니다. 각 면에 택시캡 길이가 2r이라 둘레가 8r입니다. 따라서, 택시 기하학에서 원 상수 π의 아날로그 값인 원주 대 직경의 비율은 4와 같습니다.

닫힌 공(또는 2차원 경우 닫힌 디스크)은 특정 중심으로부터의 반경보다 작거나 같은 거리에 있는 점들의 집합인 채워진 구입니다. 정사각형 격자에 있는 셀룰러 오토마타의 경우, 택시캡 디스크는 중심의 범위 r의 폰 노이만 근방입니다.

평면상에서 체비셰프 거리(L_∞ 메트릭)의 반지름 r의 원도 좌표축과 평행한 변의 길이가 2r인 정사각형이므로 평면상 체비셰프 거리는 평면 택시 거리에 대한 회전 및 스케일링으로 등가로 볼 수 있습니다. 그러나₁ L 메트릭과 L_∞ 메트릭 간의 동일성은 더 높은 차원으로 일반화되지 않습니다.

이 원들의 집합에 있는 각 쌍의 교점이 비어 있지 않은 교점을 가질 때마다 전체 집합에 대한 교점이 존재하므로 맨하탄 거리는 주입 메트릭 공간을 형성합니다.

호 길이

Let ${\displaystyle y=f(x)}$ be a continuously differentiable function in ${\displaystyle \mathbb {R} ^{2}}$. Let ${\displaystyle s}$ be the taxicab arc length of the planar curve defined by ${\displaystyle f}$ on some interval ${\displaystyle [a,b]}$. $그런$ 다음 ${\displaystyle i^{\text{th}}$의 택시 캡 길이는 ${\displaystyle {호의}_{}}$ 극소 정규 분할$$δsi ${\displaystyle${i}}와 같습니다.

${\displaystyle \Delta s_{i}=\Delta x_{i}+\Delta y_{i}=\Delta x_{i}+ f(x_{i})-f(x_{i-1}) }$

By the Mean Value Theorem, there exists some point ${\displaystyle x_{i}^{*}}$ between ${\displaystyle x_{i}}$ and ${\displaystyle x_{i-1}}$such that ${\displaystyle f(x_{i})-f(x_{i-1})=f'(x_{i}^{*})dx_{i}}$.^[7]

${\displaystyle \Delta s_{i}=\Delta x_{i}+ f'(x_{i}^{*}) \Delta x_{i}=\Delta x_{i}(1+ f'(x_{i}^{*}) )}$

$그런{\displaystyle }$ 다음 ${\displaystyle$ s$}$은${\displaystyle }$[${\displaystyle a,}$ ${\displaystyle b]}$ ${\displaystyle [a, b]$에서 임의로 작아질 때$$ ${\displaystyle s}$의 모든 파티션의 합으로 제공됩니다$$.

${\displaystyle {\begin{aligned}s&=\lim _{n\rightarrow \infty}\sum _{i=1}^{n}\Delta x_{i}(1+ f'(x_{i}^{*})\&=\int _{a}^{b}1+ f'(x) \, dx\end{aligned}}$

이를 테스트하려면 원점을 중심으로$$ 반지름 $r{\displaystyle }$ ${\displaystyle$ r$}$의 택시 원을 선택합니다. 첫 번째 사분면에 있는 곡선은 $길이$가 f${\displaystyle (x)}$ =${\displaystyle }$- ${\displaystyle x}$+ r {\displaystyle f(x) = - x+r}입니다.

${\displaystyle s=\int_{0}^{r}1+ -1 dx=2r}$

나머지 사분면을 설명하기 위해$$ 이 $값$에 4 ${\displaystyle$ 4$}$을 곱하면 ${\displaystyle \mathrm{8r}}$ ${\displaystyle 8r}$이 제공되며$,$ 이는 택시 탭 원의 둘레와 일치합니다.^[8] $이제$ 원점을 중심으로 $하는$ 반지름 r ${\display$ r$}$의 유클리드 원을 살펴보십시오. 이 ${\displaystyle \mathrm{원은}}$ f${\displaystyle (\sqrt{x^{}}}$) =$$r 2 - x 2 {\display f(x) = {\sqrt {r^{2}-x^{2}}}입니다. 1사분면의 호 길이는 다음과 같습니다.

${\displaystyle {\begin{aligned}s&=\int _{0}^{r}1+ {\frac {-x}{\sqrt {r^{2}-x^{2}}}} dx\\&=x+{\sqrt {r^{2}-x^{2}}}{\bigg }_{0}^{r}\\&=r-(-r)\\&=2r\end{aligned}}}$

나머지 사분면을 계산하면 $4{\displaystyle }$× ${\displaystyle 2}$ r = ${\displaystyle 8}$ ${\displaystyle r}${\displaystyle 4\times 2r = 8r}이 다시 나옵니다. 따라서, 택시 미터법에서 택시 원과 유클리드 원의 둘레는 같습니다.^[9] 사실, 구간${\displaystyle }$[${\displaystyle a,}$ ${\displaystyle b]}$ ${\displaystyle [a, b]$ {\displaystyle [a, b]}에 대한 $연속{\displaystyle }$ 도함수로 단조롭고 미분 가능한$$ $임의$의 함수 f ${\$$displaystyle$ $f}$에 대해$,$ [$,$ ${\displaystyle b]}$ ${\displaystyle$$f}$의 호 길이$b]}$은$($는${\displaystyle )}$ (${\displaystyle b}$ - a${\displaystyle }$)${\displaystyle }$+ $∣$${\displaystyle f}$ ( ${\displaystyle b}$ ) - $f$ ( a ) $∣$ {\displaystyle (b-a)+\mid f (b)-f (a)\mid입니다.

삼각형 합동

세 개의 대응하는 변의 거리가 같고 세 개의 대응하는 각도가 같은 경우에만 두 개의 삼각형이 합동입니다. 유클리드 기하학에서 삼각형 일치를 보장하는 여러 정리가 있는데, 즉 각도-각면(AAS), 각도-측면(ASA), 측면-각면(SAS), 측면-측면(SSS)이 있습니다. 그러나 택시 기하학에서는 SASAS만이 삼각형 일치를 보장합니다.^[11]

예를 들어, 각도가 45-90-45인 두 개의 오른쪽 이등변 택시 삼각형을 예로 들어보자. 양쪽 삼각형의 두 다리는 조세 길이가 2이지만 빗변은 합동이 아닙니다. 이 반례는 AAS, ASA 및 SAS를 제거합니다. 또한 AASS, AAAS 및 ASASA도 제거합니다. 세 개의 합동각과 두 개의 변을 갖는다고 해서 택시 기하학에서 삼각형의 합동이 보장되는 것은 아닙니다. 따라서, 택시 기하학에서 유일한 삼각형 합동 정리는 SASAS이며, 여기서 세 개의 대응하는 변은 모두 합동이어야 하고 적어도 두 개의 대응하는 각도는 합동이어야 합니다.^[12] 이 결과는 주로 택시 기하학에서 선분의 길이가 방향에 따라 달라진다는 사실 때문입니다.

적용들

압축감지

과소 결정된 선형 방정식 시스템을 해결할 때 매개 변수 벡터의 정규화 항은 벡터의$$ℓ 1 ${\displaystyle \ell$ _{1}} 노름(택시캡 기하학)으로 표현됩니다. 이 접근 방식은 압축 센싱이라는 신호 복구 프레임워크에 나타납니다.

주파수 분포의 차이

분류기하학을 사용하여 이산 주파수 분포의 차이를 평가할 수 있습니다. 예를 들어, RNA 스플라이싱에서 각 6량체가 스플라이스 부위 근처의 각 주어진 뉴클레오티드에 나타날 확률을 표시하는 6량체의 위치 분포는 L1-거리와 비교될 수 있습니다. 각 위치 분포는 각 항목이 특정 뉴클레오티드에서 시작하는 헥사머의 가능성을 나타내는 벡터로 표현될 수 있습니다. 두 벡터 사이의 L1-거리가 크다는 것은 분포의 특성에 상당한 차이가 있음을 나타내는 반면, 거리가 작다는 것은 유사한 모양의 분포를 나타냅니다. 이는 각 세그먼트의 면적이 해당 시점에서 두 곡선의 가능성 간의 절대적인 차이이므로 두 분포 곡선 사이의 면적을 측정하는 것과 같습니다. 모든 세그먼트에 대해 합산하면 L1-거리와 동일한 측정값을 제공합니다.^[14]

참고 항목

• 해밍 거리 – 이진 숫자의 두 문자열 간에 다른 비트 수
• 리 거리
• 직교 볼록 선체 – 각 축 평행선과 간격을 두고 교차하는 최소 초집합
• 계단 패러독스 – 더 미세하고 미세한 "계단 곡선"의 길이의 한계가 곡선이 향하는 대각선 세그먼트의 길이와 일치하지 않는다는 패러독스

참고문헌

더보기

• Gardner, Martin (1997). "10. Taxicab Geometry". The Last Recreations. Copernicus. pp. 159–176. ISBN 0-387-94929-1.
• Krause, Eugene F. (1975). Taxicab Geometry. Addison-Wesley. ISBN 0201039346. 도버(Dover, 1986)에 의해 재인쇄, ISBN 0-486-25202-7.

외부 링크

• Weisstein, Eric W. "Taxicab Metric". MathWorld.
• Malkevitch, Joe (October 1, 2007). "Taxi!". American Mathematical Society. Retrieved October 6, 2019.