4차원의 점 그룹

기하학에서, 4차원의 점 그룹은 3-sphere의 등계 그룹을 고정하거나 그에 상응하여 원점을 그대로 두는 4차원의 등계 그룹이다.

4차원 그룹의 역사

• 1889 Edouard Goursat, Sur les replacements et les division of Orthogonales de l'espace, Anales Scientifique de L'école Normale Sér. 3, 6, (pp. 9–102, 페이지 80–81), Goursat 4면체드론
• 1951년, A. C.헐리, 유한 회전의 그룹과 4차원의 크리스탈 클래스, 케임브리지 철학회의의 진행, 제47권, 발행 04, 페이지 650^[1]
• 1962년 L. L. 맥케이 브라바이스 4차원 공간^[2]
• 1964 Patrick du Val, Homographies, Quaternion 및 Rotation, Quaternion 기반 4D 포인트 그룹
• 1975년 얀 모즈지마스, 안드르제즈 솔레키, R4 포인트 그룹, 수학 물리학에 관한 보고서, 제7권, 제3호, 페이지 363-394
• 1978년 H. Brown, R. Bülow, J. Neubüser, H. Wondratschek 및 H. Zassenhaus, 4차원 공간의 결정학적 그룹.^[4]
• 1982년 N. P. 워너, S2와 S3의 정규 테셀레이션의 대칭군
• 1985년 E. J. W. 휘태커, 4차원 크리스탈 클래스의 하이퍼스테레오그램 지도책
• 1985년 H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, 4D 포인트 그룹에 대한 Coxeter 표기법
• 2003년 John Conway 및 Smith, On Quaternions 및 Octonion, Completed Quaternion 기반 4D 포인트 그룹
• 2018 N. W. Johnson Geometries and Transformations, 11,12,13장, Full polychoric groups, p. 249, duoprismatic groups p. 269

4D 포인트 대칭의 등각도

4차원 점 대칭의 기본 등각은 반사 대칭, 회전 대칭, 회전 대칭, 회전 대칭, 이중 회전 등 4가지로 구성된다.

그룹 표기법

이 기사는 위키피디아의 품질 기준을 충족시키기 위해 정리가 필요할 수 있다.구체적인 문제는 다음과 같다.이 글은 구조 감각이 뚜렷하지 않은 채 심하게 흐트러져 있다. 가능하다면 이 기사를 개선하는 것을 도와줘.(2021년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

이 글의 포인트 그룹은 확장된 그룹과 하위 그룹에 대한 마크업과 함께 Coxeter 그룹에 기반한 Coxeter 표기법으로 주어진다.^[6]Coxeter 표기법은 [3,3,3], [4^1,1,1,3,3], [3], [3,3], [5,3,3], [p,2,q]와 같은 Coxeter 도표와 직접 일치한다.이 그룹들은 3-sphere를 동일한 초심 4면 영역으로 묶었다.도메인 수는 그룹의 순서다.불가해한 그룹에 대한 미러 수는 nh/2이며 여기서 h는 Coxeter 그룹의 Coxeter 번호, n은 치수(4)이다.^[7]

상호 참조를 위해, 여기에 또한 Patrick ^[8]du Val(1964)과 John Conway(2003)에 의한 quaternion 기반 명단이 있다.^[9]콘웨이의 표기법은 그룹의 순서를 키랄 다면체군 순서(T=12, O=24, I=60)를 가진 원소의 산물로 계산할 수 있도록 한다.콘웨이의 표기법에서 (±) 접두사는 중심 역전을 의미하며 접미사(.2)는 거울 대칭을 의미한다.마찬가지로 두발 표기는 거울 대칭을 위한 별표(*) 위첨자를 가지고 있다.

비자발군

비자발적 집단은 대칭[ ] 없음,⁺ 반사 대칭[ ], 2배 회전 대칭[2],⁺ 2배 회전 대칭[2⁺], 2배 회전 대칭[2,2⁺⁺], 2배 회전 대칭[2배⁺ 회전], 2배 회전 대칭[2⁺,2] 등 5개가 있다.

4위 Coxeter 그룹

다육체는 4차원 일반 다육체의 5대칭군 중 하나이다.또한 3개의 다면 프리즘 그룹과 무한대의 이복선 프리즘 그룹이 있다.각 그룹은 거울 평면에 의해 경계된 구르사트 사면체 기본 영역에 의해 정의된다.거울 사이의 이음각은 이음 대칭의 순서를 결정한다.Coxeter-Dynkin 도표는 노드가 미러 평면을 나타내고 가장자리를 가지라고 하며 미러 사이의 이음각 순서로 라벨을 붙인 그래프다.

폴리초론(plolal polychora, 형용사 polychora)^[11]이라는 용어는 그리스 뿌리의 폴리("다수")와 초로스("방" 또는 "공간")에서 나왔으며, 노르만 존슨과 조지 올셰프스키가 균일한 폴리초라(4-폴리토페스)와 관련된 4차원^[10] 대칭군에서 주창한다.

직교 부분군

B는4 4A와1 D의4 두 직교 그룹으로 분해될 수 있다. = (4개의 직교 미러) = (12개의 거울)

F는4 2개의 직교 D 그룹으로4 분해될 수 있다. = (12개의 거울) = (12개의 거울)

B3×A는1 직교 그룹, 4A 및1 D로3 분해할 수 있다. = (3+1 직교 미러) = (6개의 거울)

4등급 Coxeter 그룹은 4-스페이스에 4개의 미러 세트를 허용하고 3-sphere를 4-헤드랄 기본 영역으로 나눈다.하위 등급의 Coxeter 그룹은 3-sphere의 호소헤드론 또는 호소토페 기본 도메인만 바인딩할 수 있다.

3D 다면체 그룹과 마찬가지로 주어진 4D 다면체 그룹의 이름은 해당 삼각형 모양의 일반 다면체의 셀 카운트의 그리스 접두사에 의해 구성된다.^[12]확장된 대칭은 Coxeter 다이어그램 구조 내에 대칭 링 패턴이 있는 균일한 폴리초라에 존재한다.치랄 대칭은 교대로 균일한 폴리초라에 존재한다.

Only irreducible groups have Coxeter numbers, but duoprismatic groups [p,2,p] can be doubled to [[p,2,p]] by adding a 2-fold gyration to the fundamental domain, and this gives an effective Coxeter number of 2p, for example the [4,2,4] and its full symmetry B₄, [4,3,3] group with Coxeter number 8.

바일 무리를 짓다	콘웨이 쿼터니온	추상적 구조화하다	콕시터 도표를 만들다		콕시터 표기법	주문	정류자 부분군	콕시터 번호를 붙이다 (h)	거울 (m)
전체 다색체군
A을4	+1/60[I×I].21	S5			[3,3,3]	120	[3,3,3]+	5		10
D4	±1/3[T×T]2	1/2.2S4			[31,1,1]	192	[31,1,1]+	6		12
B4	±1/6[O×O].2	2S4 = S2≀S4			[4,3,3]	384		8	4	12
F4	±1/2[O×O3].	3.2S4			[3,4,3]	1152	[3+,4,3+]	12	12	12
H4	±[I×I]2	2.(A5×A5).2			[5,3,3]	14400	[5,3,3]+	30		60
전체 다면 프리즘 그룹
A3A1	+1/24[O×O].23	S4×D1			[3,3,2] = [3,3]×[ ]	48	[3,3]+	-		6	1
B3A1	±1/24[O×O].2	S4×D1			[4,3,2] = [4,3]×[ ]	96		-	3	6	1
H3A1	±1/60[I×I]2	A5×D1			[5,3,2] = [5,3]×[ ]	240	[5,3]+	-		15	1
완전 이중주파
4A1 = 2D2	±1/2[D4×D4]	D14 = D22			[2,2,2] = [ ]4 = [2]2	16	[ ]+	4	1	1	1	1
D2B2	±1/2[D4×D8]	D2×D4			[2,2,4] = [2]×[4]	32	[2]+	-	1	1	2	2
D2A2	±1/2[D4×D6]	D2×D3			[2,2,3] = [2]×[3]	24	[3]+	-	1	1	3
D2G2	±1/2[D4×D12]	D2×D6			[2,2,6] = [2]×[6]	48		-	1	1	3	3
D2H2	±1/2[D4×D10]	D2×D5			[2,2,5] = [2]×[5]	40	[5]+	-	1	1	5
2B2	±1/2[D8×D8]	D42			[4,2,4] = [4]2	64	[2+,2,2+]	8	2	2	2	2
B2A2	±1/2[D8×D6]	D4×D3			[4,2,3] = [4]×[3]	48	[2+,2,3+]	-	2	2	3
B2G2	±1/2[D8×D12]	D4×D6			[4,2,6] = [4]×[6]	96		-	2	2	3	3
B2H2	±1/2[D8×D10]	D4×D5			[4,2,5] = [4]×[5]	80	[2+,2,5+]	-	2	2	5
2A2	±1/2[D6×D6]	D32			[3,2,3] = [3]2	36	[3+,2,3+]	6	3		3
A2G2	±1/2[D6×D12]	D3×D6			[3,2,6] = [3]×[6]	72		-	3		3	3
2G2	±1/2[D12×D12]	D62			[6,2,6] = [6]2	144		12	3	3	3	3
A2H2	±1/2[D6×D10]	D3×D5			[3,2,5] = [3]×[5]	60	[3+,2,5+]	-	3		5
G2H2	±1/2[D12×D10]	D6×D5			[6,2,5] = [6]×[5]	120		-	3	3	5
2H2	±1/2[D10×D10]	D52			[5,2,5] = [5]2	100	[5+,2,5+]	10	5		5
일반적으로 p,q=2,3,4...
2I2(2p)	±1/2[D4p×D4p]	D2p2			[2p,2,2p] = [2p]2	16p2	[p+,2,p+]	2p	p	p	p	p
2I2(p)	±1/2[D2p×D2p]	Dp2			[p,2,p] = [p]2	4p2		2p	p		p
I2(p)I2(q)	±1/2[D4p×D4q]	D2p×D2q			[2p,2,2q] = [2p]×[2q]	16pq	[p+,2,q+]	-	p	p	q	q
I2(p)I2(q)	±1/2[D2p×D2q]	Dp×Dq			[p,2,q] = [p]×[q]	4pq		-	p		q

대칭 순서는 일반 폴리초론의 세포 수에 그 세포의 대칭을 곱한 것과 같다.전분해 이중 폴리초라에는 대칭 그룹의 기본 영역과 일치하는 세포가 있다.

볼록한 일반 4폴리톱 및 전분포 이중고를 위한 그물

대칭	A을4	D4	B4	F4	H4
4칸짜리	5세포	반신반의하다	큐테릭트	24셀	120 셀
세포	5 {3,3}	16 {3,3}	8 {4,3}	24 {3,4}	120 {5,3}
세포 대칭	[3,3] 주문 24		[4,3] 주문 48		[5,3], 120번 주문
콕시터 다이어그램		=
4칸짜리 그물을 치다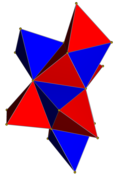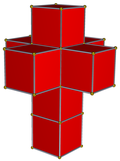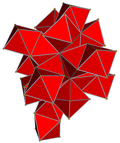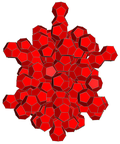
잡식성	옴니 5셀	전미적격.	전미 테서락트	옴니 24셀	옴니로120셀
잡식성 이중의 그물을 치다
콕시터 다이어그램
세포	5×24 = 120	(16/2)×24 = 192	8×48 = 384	24×48 = 1152	120×120 = 14400

치랄 부분군

반사형 4차원 점 그룹의 직접 부분군은 다음과 같다.

콕시터 표기법		콘웨이 쿼터니온	구조	주문	회전 축
다핵군
	[3,3,3]+	+1/60[I×I]	A을5	60			103	102
	[[3,3,3]]+	±1/60[I×I]	A5×Z2	120			103	(10+?)2
	[31,1,1]+	±1/3[T×T]	1/2.2A4	96			163	182
	[4,3,3]+	±1/6[O×O]	2A4 = A2≀A4	192	64		163	362
	[3,4,3]+	±1/2[O×O]	3.2A4	576	184	163	163	722
	[3+,4,3+]	±[T×T]		288		163	163	(72+18)2
	[[3+,4,3+]]	±[O×T]		576			323	(72+18+?)2
	[[3,4,3]]+	±[O×O]		1152	184		323	(72+?)2
	[5,3,3]+	±[I×I]	2.(A5×A5)	7200		725	2003	4502
다면 프리즘 그룹
	[3,3,2]+	+1/24[O×O]	A4×Z2	24		43	43	(6+6)2
	[4,3,2]+	±1/24[O×O]	S4×Z2	48		64	83	(3+6+12)2
	[5,3,2]+	±1/60[I×I]	A5×Z2	120		125	203	(15+30)2
두족주의 집단
	[2,2,2]+	+1/2[D4×D4]		8		12	12	42
	[3,2,3]+	+1/2[D6×D6]		18		13	13	92
	[4,2,4]+	+1/2[D8×D8]		32		14	14	162
(p,q=2,3,4...), gcd(p,q)=1
	[p,2,p]+	+1/2[D2p×D2p]		2p2		1p	1p	(pp)2
	[p,2,q]+	+1/2[D2p×D2q]		2pq		1p	1q	(pq)2
	[p+,2,q+]	+[Cp×Cq]	Zp×Zq	p q.		1p	1q

펜타코리아 대칭

• 펜타코리아 그룹 – A₄, [3,3,3], (), 120, (Du Val #51' (I^†/C₁;I/C₁),^†* 콘웨이 +/[¹₆₀I×I₁]. 링이 달린 콕시터 다이어그램으로 주어진 5 셀(펜타코론)에 이름을 붙였다.사면체군[3,3]을 확장하기 위해 초면체군이라고도 한다.이 그룹에는 10개의 미러 하이퍼플레인이 있다.추상대칭군 S에₅ 대해 이형적이다.
  • 확장된 펜타코리아 그룹, Auto(A₄), [3,3,3], (배중되는 것은 접힌 도표로 암시할 수 있음), 240, (Du Val #51 (I^†*/C₂;I/C₂),^†* Conway ±/[¹₆₀I×I].추상적인 그룹의 직접적인₅ 생산물인 S×C와₂ 이형적이다.
    • 치랄 확장형 펜타코리아 그룹은 [3,3,3],⁺ (), 주문 120, (Du Val #32 (I^†/C₂;I/C₂),^† Conway ±/[¹₆₀IxI])이다.이 집단은 비록 균일하게 만들 수는 없지만, 전지 5-셀의 건설을 대표한다.그것은 추상적인 그룹의 직접적인 생산물인 A₅×C와₂ 이형적이다.
  • 치랄 오타코리아 그룹은 [3,3,3],⁺ (), 오더 60, (Du Val #32' (I^†/C₁;I/C₁),^† 콘웨이 +/[¹₆₀I×I])이다.추상적인 대체 집단인₅ A와 이형적이다.
    • 확장 치랄 오타코리아 그룹은 [3,3,3]],⁺ 주문 120, (Du Val #51" (I^†/C₁;I/C₁),_–^†* 콘웨이 +/[¹₆₀IxI]이다.2₃. Coxeter는 이 집단을 추상집단(4,6 2,3)과 연관시킨다.^[13]추상 대칭군 S에도₅ 이형이다.

육각 대칭

• Hexadecachoric group – B₄, [4,3,3], (), order 384, (Du Val #47 (O/V;O/V)^*, Conway ±¹/₆[O×O].2), named for the 16-cell (hexadecachoron), . There are 16 mirror hyperplanes in this group, which can be identified in 2 orthogonal sets: 12 from a [3^1,1,1] subgroup, and 4 from a [2,2,2] subgroup.3D 옥타헤드 그룹[4,3]을 확장하는 것을 초옥타헤드 그룹이라고 부르기도 하며, 큐브 그룹의 경우 큐브 그룹인 테서랙트 그룹이라고도 한다.
  • 키랄 육각류 그룹은 [4,3,3],⁺ (), 순서 192, (Du Val #27 (O/V;O/V), 콘웨이 ±/[¹₆O×O])이다.이 집단은 비록 균일하게 만들 수는 없지만, 전미수막의 건설을 나타낸다.
  • 이온 감소된 육각류 그룹은 [4, (3,3)],⁺ (), 순서 192, (Du Val #41 (T/V;T/V),^* Conway ±/[¹₃TXT].이 그룹은 건설과 함께 24-셀의 스너브로 이어진다.
  • 반육각형 그룹은 [1⁺,4,3,3,3], ( = ), 순서 192이며, #demistic 대칭과 동일하다. [3^1,1,1].이 그룹은 16-셀의 4차 대체 구조로 표현된다. = .
    • 그룹 [1⁺,4, (3,3)],⁺ ( = ), 순서 96, 그리고 치랄 소수성 그룹[3^1,1,1]⁺과 동일하며, 또한 [4,3,3]의 정류자 하위 그룹이다.
  • 고지수 반사 부분군은 프리즘적 팔면 대칭인 [4,3,2] (), 순서 96, 부분군 지수 4, (Du Val #44 (O/C₂;O/C₂),^* 콘웨이 ¹₂₄±/[O×O].잘린 입방 프리즘은 Coxeter 도표와 대칭을 이루고 있으며 입방 프리즘은 과 같이 큐빅트의 낮은 대칭 구조다.
    • 그것의 키랄 부분군은 [4,3,2],⁺ (), 순서 48, (Du Val #26 (O/C₂;O/C₂), 콘웨이 ±/[¹₂₄O×O])이다.예를 들어, 스너브 큐빅 항정신병증이 있다. 비록 그것이 균일하게 만들어질 수는 없지만 말이다.
    • 이온 부분군은 다음과 같다.
      • [(3,4),⁺2], (), 주문 48, (Du Val #44b' (O/C₁;O/C₁),₋^* Conway +/[¹₂₄O×O₁].스너브 입방 프리즘은 Coxeter 도표와 대칭을 이룬다.
        • [(3,4),⁺2⁺], (), 24, (Du Val #44' (T/C₂;T/C₂),₋^* 콘웨이 +/[¹₁₂T×T]2₁]를 주문한다.
      • [4,3⁺,2], (), 주문번호 48, (Du Val #39 (T/C₂;T/C₂),_c^* 콘웨이 ±/[¹₁₂T×T].
        • [4,3⁺,2,1⁺] = [4,3⁺,1] = [4,3⁺], ( = ), 주문 24, (Du Val #44" (T/C₂;T/C₂),^* Conway +/[¹₁₂T×T₃].이것은 3D 피리토헤드 그룹 [4,3⁺] 입니다.
        • [3⁺,4,2⁺], (), 24, (Du Val #21 (T/C₂;T/C₂), 콘웨이 ±/[¹₁₂T×T])를 주문한다.
      • [3,4,2⁺], (), 주문 48, (Du Val #39' (T/C₂;T/C₂),₋^* 콘웨이 ±/[¹₁₂T×T]2).
      • [4, (3,2)],⁺ (), 주문 48, (Du Val #40b') (O/C₁;O/C₁),₋^* 콘웨이 +/[¹₂₄O×O₁].
    • 절반 부분군 [4,3,2,1⁺] = [4,3,1] = [4,3], ( = ), 주문 48(Du Val #44b" (O/C₁;O/C₁),_c^* Conway +/[¹₂₄O×O₃].팔면 피라미드 그룹으로 불리며 3D 팔면 대칭이다[4,3].입방피라미드는 Schléfli 기호를 사용하여 이러한 대칭을 가질 수 있다: ( ) ∨ {4,3}.
      

      [4,3], ,, 팔면 피라미드 그룹은 이형에서 3차원 팔면 대칭이다.
      • 치랄 반쪽 부분군 [(4,⁺3,2,1⁺] = [4,3,1]⁺ = [4,3],⁺ ( = ), 순서 24 (Du Val #26b' (O/C₁;O/C₁), 콘웨이 +/[¹₂₄O×O]).이것은 3D 치랄 팔면체 그룹 [4,3]⁺이다.스너브 입방피라미드는 Schléfli 기호 ( )와 함께 이러한 대칭을 가질 수 있다: with sr{4,3}.
  • 또 다른 높은 지수 반영 부분군은 프리즘적 사면 대칭, [3,3,2], (), 순서 48, 부분군 지수 8, (Dual Val #40b" (O/C₁;O/C₁),^* 콘웨이 +/[¹₂₄O×O₃].
    • 치랄 부분군은 [3,3,2,2],⁺ (), 순서 24, (Du Val #26b" (O/C₁;O/C₁), 콘웨이 +/[¹₂₄O×O])이다.예를 들면, 사면체 항정신병증이 있다. 비록 그것이 균일하게 만들어질 수는 없지만 말이다.
    • 이온 부분군은 [(3,3),⁺2], (), 순서 24, (Du Val #39b' (T/C₁;T/C₁),_c^* Conway +/[¹₁₂T×T].2₃)이다.예를 들어, 스너브 사면 프리즘이 있다.
    • 절반 부분군은 [3,3,2,1⁺] = [3,3,1] = [3,3], ( = ) 순서 24, (Du Val #39b" (T/C₁;T/C₁),₋^* 콘웨이 +/[¹₁₂T×T₁].사면 피라미드 그룹이라고 불리며 3D 사면체 그룹이다[3,3].일반 사면 피라미드는 Schléfli 기호를 사용하여 이러한 대칭을 가질 수 있다: ( ) ∨ {3,3}.
      

      [3,3], , 사면 피라미드 그룹은 이형에서 3차원 사면 대칭이다.
      • 치랄 반쪽 부분군 [(3,3],⁺2⁺,1] = [3,⁺3]( = ), 12,(Du Val #21b' (T/C₁;T/C₁), Conway +/[¹₁₂T×T])를 주문한다.이것은 3D 치랄 4면체 그룹 [3,3]⁺이다.스너브 사면 피라미드는 Schléfli 기호 ( )와 함께 이러한 대칭을 가질 수 있다: ( ) symmetry sr{3,3.
  • 또 다른 고지수 방사반사 부분군은 [4, (3,3)],^* 색인 24, 순서 3 이음각의 거울을 제거하여 [2,2] (), 순서 16을 생성한다.그 외는 [4,2,4] (), [4,2,2] (), 부분군 지수 6, 12, 순서 64, 32이다.이러한 그룹은 테서락트(), ()의 하위 대칭이다.이 집단은 #이중주의 대칭이다.

이코시테트라코리아 대칭

• Icositetrachoric group – F₄, [3,4,3], (), order 1152, (Du Val #45 (O/T;O/T)^*, Conway ±¹/₂[OxO].2), named for the 24-cell (icositetrachoron), . There are 24 mirror planes in this symmetry, which can be decomposed into two orthogonal sets of 12 mirrors in demitesseractic symmetry [3^1,1,1] subgroups, as [3^*,4,3] and [3,4,3^*], as index 6 subgroups.
  • 확장된 이코사테트라코리아 그룹인 Aut(F₄), [3,4,3], (Du Val #48 (O/O;O/O),^* Conway ±[O×O].
    • 치랄 확장 이코시테트라코리아 그룹 [3,4,3],()⁺은 1152, (Du Val #25 (O/O;O/O), 콘웨이 ±[OxO])의 순서가 있다.이 집단은 균일하게 만들 수는 없지만, 전지 24-셀의 건설을 대표한다.
  • 이온 감소된 이온성 그룹은 576, (Du⁺ Val #43 (T/T;T⁺/T),^* 콘웨이 ±[TXT].2)의 순서가 있다.이 그룹은 시공 또는 가공을 통해 스너브 24 셀로 이어진다.
    • 이중 감소된 이코사테트라코리아 그룹 [3⁺,4,3⁺] (이중 감소는 도표 4-분지: ), 순서 288, (듀발 #20 (T/T;T/T), 콘웨이 ±[TXT])은 [3,4,3]의 정류자 하위그룹이다.
      • [3,4⁺,3⁺], ()주문 576, (Du Val #23 (T/T;O/O), 콘웨이 ±[OxT])로 연장할 수 있다.
  • 치랄 이코시테트라코리아 그룹은 [3,4,3],⁺ (), 순서 576, (Du Val #28 (O/T;O/T), Conway ±/[¹₂O×O])이다.
    • 확장 치랄 이코시테트라코리아 그룹[3,4,3]⁺은 1152, (Du Val #46 (O/T;O/T),₋^* Conway ±/[¹₂OxO].2)의 순서를 가지고 있다.Coxeter는 이 그룹을 추상 그룹(4,8 2,3)과 연관시킨다.^[13]

소수점 대칭

• Demitesseractic group – D₄, [3^1,1,1], [3,3^1,1] or [3,3,4,1⁺], ( = ), order 192, (Du Val #42 (T/V;T/V)₋^*, Conway ±¹/₃[T×T].2), named for the (demitesseract) 4-demicube construction of the 16-cell, or . There are 12 mirrors in this symmetry group.
  • 거울을 추가하여 확장된 대칭에는 두 가지 유형이 있다: 거울에 의해 기본 영역을 이등분하여 [4,3,3]이 되고, 3방향으로 확장된 전체 그룹 [3^1,1,1]이 [3,3^1,1]이 된다.
  • 키랄 강하군은 [3^1,1,1]⁺ 또는 [1⁺,4,(3,3)],⁺ ( = ), 순서 96, (Du Val #22 (T/V;T/V), 콘웨이 ±/[¹₃T×T]이다.이 그룹은 시공 = .와 함께 스너브 24 셀로 이어진다.

육각 대칭

[5,3,3]+ 72개의 순서-5 교량	[5,3,3]+ 200회의 주문-3 교량
[5,3,3]+ 450개의 주문-2 자이스	[5,3,3]+ 모든 교량
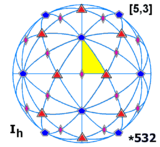[5,3], , 이등각피라미드 그룹은 이등각과 3차원 이등각 대칭이다.

• Hexacosichoric group – H₄, [5,3,3], (), order 14400, (Du Val #50 (I/I;I/I)^*, Conway ±[I×I].2), named for the 600-cell (hexacosichoron), . It is also sometimes called the hyper-icosahedral group for extending the 3D icosahedral group [5,3], and hecatonicosachoric group or dodecacontachoric group from the 120-cell, .
  • 키랄 육각체군은 [5,3,3],⁺ (), 순서 7200, (Du Val #30 (I/I;I/I), 콘웨이 ±[I×I])이다.이 그룹은 스너브 120 셀의 건설을 대표하지만, 균일하게 만들 수는 없다.
  • 고지수 반사 부분군은 프리즘적 동면 대칭, [5,3,2], (), 순서 240, 부분군 지수 60, (Du Val #49 (I/C₂;I/C₂),^* 콘웨이 ¹₆₀±/[IxI]이다.2).
    • 그것의 키랄 부분군은 [5,3,2],⁺ (), 주문 120, (Du Val #31 (I/C₂;I/C₂), Conway ±/[¹₆₀IxI])이다.이 집단은 비록 균일하게 만들 수는 없지만, 스누브 도데카랄 항정신병증의 건설을 대표한다.
    • 이온 하위 그룹은 [(5,3),⁺2], (), 순서 120, (Du Val #49' (I/C₁;I/C₁₁),^* Conway +/[¹₆₀IxI].이 그룹은 snub deadecheadral 프리즘의 건설을 나타낸다.
    • 반쪽 부분군은 [5,3,2⁺,1] = [5,3,1] = [5,3], ( = ) 순서 120, (Du Val #49"), (I/C₁;I/C₁),₋^* 콘웨이 +/[¹₆₀IxI]이다.2₃. 이두각피라미드 그룹으로 불리며, 3D 이두각피라미드 그룹 [5,3]이다.일반 도데카메랄 피라미드는 슐레플리 기호 ( )와 함께 이러한 대칭을 가질 수 있다: ( ) ∨ {5,3}.
      • 치랄 반쪽 부분군은 [(5,3],⁺ 2,1⁺] = [5,3,1]⁺ = [5,3],⁺ ( = ), 오더 60, (Du Val #31')(I/C₁;I/C₁), 콘웨이 +/[¹₆₀IxI]이다.이것은 3D 치랄 이코사드랄 그룹 [5,3]⁺이다.스너브 도데카헤드랄 피라미드는 Schléfli 기호 ( )와 함께 이러한 대칭을 가질 수 있다: ( ) symmetry sr{5,3.

이항 대칭

• 2개의 두 개의 그룹 – [p,2,q], (), 순서 4pq는 모두 2 ≤ p,q < ∞에 존재한다.이 대칭에는 p+q 거울이 있는데, 이 거울은 경미하게 분음 대칭의 p와 q 거울의 두 직교 집합으로 분해된다: [p]와 [q].
  • 치랄 부분군은 [p,2,p],()⁺로, 순서 2pq이다.[2p,2,2p]⁺로 곱할 수 있다.
  • p와 q가 같을 경우 [p,2,p], (), 대칭은 [p,2,p], ()로 2배로 할 수 있다.
    • 이중: [p⁺,2,p⁺], (), [2p,2,2p⁺], [2p⁺,2⁺,2p⁺]], [2p,2,2p]].
  • [p,2,time], (), 3-공간의 선 그룹을 나타낸다.
  • [1968,2,198], () 두 세트의 평행거울과 직사각형 영역(또는 비폴드 *2222)으로 이루어진 유클리드 평면 대칭을 나타낸다.
  • 부분군에는 [p⁺,2,q], (), [p,2,q⁺], (), [p⁺,2,q⁺], ()가 포함된다.
  • 짝수 값인 경우: [2p,2⁺,2q](), [2p,2⁺,⁺2q⁺], [2p,2], [2p,2],⁺ [2q],⁺ [2p⁺,2⁺,2q⁺⁺], [2p⁺,2q],⁺ 공동작업자 부분군, 색인 16, [2p⁺,2⁺,2q⁺], (), [2q], [2q],⁺ (),
• Digonal duoprismatic group – [2,2], (), 순서 16.
  • 치랄 부분군은 [2,2,2],⁺ (), 순서 8이다.
  • 확장 [[2,2]], (), 주문 32.4-4 duoprism은 이렇게 확장된 대칭을 가지고 있다.
    • 키랄 확장 그룹은 [2,2],⁺ 순서 16이다.
    • 확장 치랄 부분군은 [2,2]],⁺ 순서 16이며, 회전 선택 생성기가 있다.추상군(4,4 2,2)과는 이형이다.
  • 기타 확장 [(3,3)[2,2]=[4,3,3], 순서 384, #헥사데카치오르 대칭큐빅은 또는 로서 대칭이 대칭은
  • 이온 감소된 부분군은 [2⁺,2,2] 순서 8이다.
    • 이중으로 줄어든 부분군은 [2⁺,2,2⁺] 순서 4이다.
      • [2⁺,2⁺]로 확장, 8번 주문.
    • 회전 선택 부분군은 [2⁺,2⁺,2], [2,2⁺,2⁺], [2⁺,2],⁺ [2,2], [(2,2]), [(2,2⁺]⁺ 순서 4이다.
    • 세 배 감소된 부분군은 [2⁺,2⁺,2⁺], (), 순서 2이다.2중 2회전, 4D 중심 반전이다.
  • 반 부분군은 [1⁺,2,2]=[1,2,2] 순서 8이다.
• 삼각 이분법 그룹 – [3,2,3], , 주문 36.
  • 치랄 부분군은 [3,2,3]⁺ 순서 18이다.
  • 확장 [3,2,3], 주문 72.3-3 duoprism은 이렇게 확장된 대칭을 가지고 있다.
    • 키랄 확장 그룹은 [3,2,3],⁺ 순서 36이다.
    • 확장 치랄 부분군은 [3,2,3],⁺ 순서 36이며, 회전 선택 생성기가 있다.추상군(4,4 2,3)과는 이형이다.
  • 기타 확장 [3], [2,3], [3,2,], [3], 주문 72, 그리고 [6,2,3] 및 [3,2,6]까지 이형이다.
  • 그리고 [3], [2], [3], [144], [6,2,6], [6,2,6]
  • 그리고 [[3], [2], [3], 순서 288, [6,2,6]까지 이형.6–6 듀오프리즘은 또는 .와 같이 이러한 대칭을 가지고 있다.
  • 이온 감소된 부분군은 [3⁺,2,3], [3,2,3⁺], 순서 18이다.
    • 이중으로 줄어든 부분군은 [3⁺,2,3⁺] 순서 9이다.
      • [3⁺,2,3⁺]로 확장, 18번 주문.
  • 높은 지수 부분군은 [3,2] , 순서 12, 지수 3이며, 이는 3차원 그룹에서 이음 대칭에 이형이다. [3,2], D_3h.
    • [3,2],⁺ 주문 6
• 제곱 이분법 그룹 – [4,2,4], , 순서 64.
  • 치랄 부분군은 [4,2,4],⁺ 순서 32이다.
  • 확장 [4,2,4], 주문 128.4-4 듀오프리즘은 이런 확장된 대칭을 가지고 있다.
    • 치랄 확장 그룹은 [4,2,4],⁺ 순서 64이다.
    • 확장 치랄 부분군은 [4,2,4]],⁺ 순서 64, 회전 선택 발생기.추상군(4,4 2,4)과는 이형이다.
  • 기타 확장 [4], 2,4], [4,2,[4], 순서 128, [8,2,4], [4,2], [4,8]까지 이형이다.4-8 듀오프리즘은 또는 .와 같이 이러한 대칭을 가지고 있다.
  • 그리고 [4], [2], [4], [8,2,8], [256], [8,2,8]로 이형화된다.
  • 그리고 [[4], [2], [4], 512, [8,2,8]까지 이형화한다.8-8 듀오프리즘은 이러한 대칭성을 가지고 있다.
  • 이온 감소된 부분군은 [4⁺,2,4], [4,2,4⁺], 순서 32이다.
    • 이중으로 줄어든 부분군은 [4⁺,2,4⁺] 순서 16이다.
      • [4⁺,2,4⁺]로 확장, 32번 주문.
    • 회전 선택 부분군은 [4⁺,2⁺,4], [4,2⁺,4⁺], [4⁺,(2,4)],⁺ [(4,2),⁺4⁺], (, , , ) 순서 16이다.
    • 세 배 감소된 부분군은 [4⁺,2⁺,4⁺], (), 순서 8이다.
  • 반 부분군은 [1,4⁺,2,4]=[2,2,4], (), [4,2,1⁺]=[4,2,2], (), 순서 32이다.
    • [1⁺,4,2,4]=[⁺2,4]=[⁺4,2,4⁺], (), ⁺[4,2,1]=[4,2,2],⁺ (), 순서 16.
  • 다시 절반의 부분군은 [1⁺,4,2,4,1⁺]=[2,2], (), 순서 16이다.
    • [1⁺,4,2,4,1⁺]⁺ = [1⁺,4,2⁺,4,1⁺] = [2,2,2],⁺ () 순서 8

일부 4차원 점 그룹 요약

이것은 콕시터 표기법으로 4차원 점군들을 요약한 것이다.그 중 227개는 결정학적 점군(p와 q의 특정 값)이다(^[14][which?]nc). (nc)는 비기록학적 그룹에 주어진다.일부 결정학적 그룹은^[which?] 추상적 그룹 구조에 따라 주문을 색인화(주문.index)한다.^[15]

유한군
[ ]: 기호 주문 [1]+ 1.1 [1] = [ ] 2.1 [2]: 기호 주문 [1+,2]+ 1.1 [2]+ 2.1 [2] 4.1 [2,2]: 기호 주문 [2+,2+]+ = [(2+,2+,2+)] 1.1 [2+,2+] 2.1 [2,2]+ 4.1 [2+,2] 4.1 [2,2] 8.1 [2,2,2]: 기호 주문 [(2+,2+,2+,2+)] = [2+,2+,2+]+ 1.1 [2+,2+,2+] 2.1 [2+,2,2+] 4.1 [(2,2)+,2+] 4 [[2+,2+,2+]] 4 [2,2,2]+ 8 [2+,2,2] 8.1 [(2,2)+,2] 8 [[2+,2,2+]] 8.1 [2,2,2] 16.1 [[2,2,2]]+ 16 [[2,2+,2]] 16 [[2,2,2]] 32	[p]: 기호 주문 [p]+ p [p] 2p [p,2]: 기호 주문 [p,2]+ 2p [p,2] 4p [2p,2+]: 기호 주문 [2p,2+] 4p [2p+,2+] 2p [p,2,2]: 기호 주문 [p+,2,2+] 2p [(p,2)+,2+] 2p [p,2,2]+ 4p [p,2,2+] 4p [p+,2,2] 4p [(p,2)+,2] 4p [p,2,2] 8p [2p,2+,2]: 기호 주문 [2p+,2+,2+]+ p [2p+,2+,2+] 2p [2p+,2+,2] 4p [2p+,(2,2)+] 4p [2p,(2,2)+] 8p [2p,2+,2] 8p	[p,2,q]: [(p,2)+,2q]: 기호 주문 [p+,2,q+] p q. [p,2,q]+ 2pq [p+,2,q] 2pq [p,2,q] 4pq 기호 주문 [(p,2)+,2q+] 2pq [(p,2)+,2q] 4pq [2p,2,2q]: 기호 주문 [2p+,2+,q+]=+ [(2p+,2+,2q+,2+)] p q. [2p+,2+,2q+] 2pq [2p,2+,2q+] 4pq [((2p,2),(+2q,2)]+ 4pq [2p,2+,2q] 8pq [[p,2,p]: 기호 주문 [[p+,2,p+]] 2p2 [[p,2,p]]+ 4p2 [[p,2,p]+] 4p2 [[p,2,p]] 8p2 [[2p,2,2p]: 기호 주문 [[(2p+,2+,2p+,2+)] 2p2 [[2p+,2+,2p+] 4p2 [[((2p,2),(+2p,2)]]+ 8p2 [[2p,2+,2p] 16p2	[3,3,2]: 기호 주문 [(3,3)Δ,2,1+] ≅ [2,2]+ 4 [(3,3)Δ,2] ≅ [2,(2,2)+] 8 [(3,3)⅄,2,1+] ≅ [4,2+] 8 [(3,3)+,2,1+] = [3,3]+ 12.5 [(3,3)⅄,2] ≅ [2,4,2+] 16 [3,3,2,1+] = [3,3] 24 [(3,3)+,2] 24.10 [3,3,2]+ 24.10 [3,3,2] 48.36 [4,3,2]: 기호 주문 [1+,4,3+,2,1+] = [3,3]+ 12 [3+,4,2+] 24 [(3,4)+,2+] 24 [1+,4,3+,2] = [(3,3)+,2] 24.10 [3+,4,2,1+] = [3+,4] 24.10 [(4,3)+,2,1+] = [4,3]+ 24.15 [1+,4,3,2,1+] = [3,3] 24 [1+,4,(3,2)+] = [3,3,2]+ 24 [3,4,2+] 48 [4,3+,2] 48.22 [4,(3,2)+] 48 [(4,3)+,2] 48.36 [1+,4,3,2] = [3,3,2] 48.36 [4,3,2,1+] = [4,3] 48.36 [4,3,2]+ 48.36 [4,3,2] 96.5 [5,3,2]: 기호 주문 [(5,3)+,2,1+] = [5,3]+ 60.13 [5,3,2,1+] = [5,3] 120.2 [(5,3)+,2] 120.2 [5,3,2]+ 120.2 [5,3,2] 240(nc)	[31,1,1]: 기호 주문 [31,1,1]Δ ≅[[4,2+,4]]+ 32 [31,1,1]⅄ 64 [31,1,1]+ 96.1 [31,1,1] 192.2 <[3,31,1]> = [4,3,3] 384.1 [3[31,1,1]] = [3,4,3] 1152.1 [3,3,3]: 기호 주문 [3,3,3]+ 60.13 [3,3,3] 120.1 [[3,3,3]]+ 120.2 [[3,3,3]+] 120.1 [[3,3,3]] 240.1 [4,3,3]: 기호 주문 [1+,4,(3,3)Δ] = [31,1,1]Δ ≅[[4,2+,4]]+ 32 [4,(3,3)Δ] = [2+,4[2,2,2]+] ≅[[4,2+,4]] 64 [1+,4,(3,3)⅄] = [31,1,1]⅄ 64 [1+,4,(3,3)+] = [31,1,1]+ 96.1 [4,(3,3)⅄] ≅ [[4,2,4]] 128 [1+,4,3,3] = [31,1,1] 192.2 [4,(3,3)+] 192.1 [4,3,3]+ 192.3 [4,3,3] 384.1 [3,4,3]: 기호 주문 [3+,4,3+] 288.1 [3,4,3⅄] = [4,3,3] 384.1 [3,4,3]+ 576.2 [3+,4,3] 576.1 [[3+,4,3+]] 576(nc) [3,4,3] 1152.1 [[3,4,3]]+ 1152(nc) [[3,4,3]+] 1152(nc) [[3,4,3]] 2304(nc) [5,3,3]: 기호 주문 [5,3,3]+ 7200(nc) [5,3,3] 14400(nc)

참고 항목

• 점군
• 2차원의 점 그룹
• 3차원의 점 그룹

참조

• H.S.M. Coxeter, 일반 폴리토페스, 제3판 도버 뉴욕, 1973년
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6
  • (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380–407, MR 2,10]
  • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559–591]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3–45]
• H.S.M. Coxeter와 W. O. J. Moser.이산 그룹용 생성기 및 관계 4번째 에드 스프링어-버래그.뉴욕, 1980년 p92, p122
• 존.H.콘웨이와 M.J.T. 가이: 4차원 아르키메데스 폴리토페스, 코펜하겐에서의 볼록성에 관한 콜로키움의 진행, 1965년 38페이지/39페이지
• N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
• N.W. Johnson: 기하학과 변환, (2018) ISBN 978-1-107-10340-5장 11: 유한대칭 그룹, 11.5 구형 Coxeter 그룹, 페이지 249
• 존 H. 콘웨이와 데릭 A.Smith, On Quaternions and Octonion, 2003, ISBN 978-1-56881-134-5
• 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장)

외부 링크

• Weisstein, Eric W. "Uniform polychoron". MathWorld.
• Klitzing, Richard. "4D uniform polytopes".