라플라스-룽지-렌츠 벡터
Laplace–Runge–Lenz vector고전역학에서 라플라스-룬지-렌츠 벡터(, LRL)는 쌍성이나 항성 주위를 도는 행성 등 한 천체가 다른 천체를 도는 궤도의 모양과 방향을 설명하는 데 주로 사용되는 벡터입니다. 뉴턴 중력에 의해 상호작용하는 두 물체의 경우, LRL 벡터는 궤도상 어디에서 계산되든 동일한 운동 상수이며,[1][2] 이와 동등하게 LRL 벡터는 보존된다고 합니다. 더 일반적으로, LRL 벡터는 두 물체 사이의 거리의 역제곱으로 변하는 중심 힘에 의해 상호작용하는 모든 문제에서 보존됩니다. 그러한 문제를 케플러 문제라고 합니다.[3][4][5][6]
수소 원자는 쿨롱의 정전기 법칙에 의해 상호 작용하는 두 개의 하전 입자, 즉 또 다른 역제곱 중심력으로 구성되기 때문에 케플러 문제입니다. LRL 벡터는 슈뢰딩거 방정식이 개발되기 [7][8]전에 수소 원자 스펙트럼의 첫 양자역학적 유도에서 필수적이었습니다. 그러나 이 접근법은 오늘날 거의 사용되지 않습니다.
고전역학과 양자역학에서 보존된 양은 일반적으로 계의 대칭에 해당합니다.[9] LRL 벡터의 보존은 특이한 대칭에 해당합니다. 케플러 문제는 수학적으로 4차원 (초)구 표면에서 자유롭게 움직이는 입자와 동일하므로 [10]4차원 공간의 특정 회전 하에서 전체 문제가 대칭입니다.[11] 이러한 더 높은 대칭성은 케플러 문제의 두 가지 특성에서 비롯됩니다: 속도 벡터는 항상 완벽한 원을 따라 움직이고, 주어진 총 에너지에 대해 모든 속도 원은 동일한 두 점에서 서로 교차합니다.[12]
라플라스-룽지-렌츠 벡터는 피에르-시몽 드 라플라스, 칼 룽지, 빌헬름 렌츠의 이름을 따서 붙여졌습니다. 라플라스 벡터,[13][14] 룽지-렌츠 벡터[15], 렌츠 벡터로도 알려져 있습니다.[8] 아이러니하게도, 그 과학자들 중 아무도 그것을 발견하지 못했습니다.[15] LRL 벡터는 여러 번 재발견 및 재공식화되었습니다.[15] 예를 들어, 그것은 천체 역학의 무차원 이심률 벡터와 동등합니다.[2][14][16] 특수 상대성 이론, 전자기장 및 심지어 다른 유형의 중심 힘의 효과를 통합하는 LRL 벡터의 다양한 일반화가 정의되었습니다.[17][18][19]
맥락
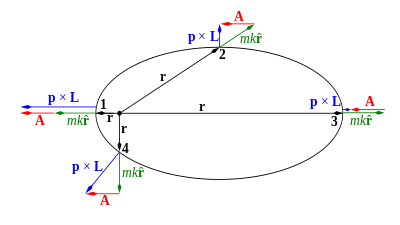
보수적인 중심 힘 아래에서 움직이는 단일 입자는 힘의 중심에 대해 총 에너지 E와 각운동량 벡터 L의 세 개의 직각 성분의 네 가지 운동 상수를 갖습니다.[20][21] 입자의 궤도는 입자의 초기 운동량 p(또는 이와 동등하게 속도 v)와 입자와 힘의[20][21] 중심 사이의 벡터 r에 의해 정의되는 평면에 국한됩니다(그림 1 참조). 이 운동면은 일정한 각운동량 벡터 L = r × p와 수직입니다. 이것은 벡터 도트 곱 방정식 r ⋅ L = 0으로 수학적으로 표현될 수 있습니다. 아래의 수학적 정의를 고려할 때, Laplace-Runge-Lenz 벡터(LRL 벡터) A는 모든 중심 힘(A ⋅ L = 0)에 대해 항상 일정한 각운동량 벡터 L에 수직입니다. 따라서 A는 항상 운동의 평면에 놓여 있습니다. 아래와 같이 A는 힘의 중심에서 운동의 근일점, 가장 가까이 접근하는 지점을 가리키며, 그 길이는 궤도의 이심률에 비례합니다.[1]
LRL 벡터 A는 길이와 방향이 일정하지만, 역제곱 중심 힘에 대해서만 일정합니다.[1] 다른 중심 힘의 경우, 벡터 A는 일정하지 않고 길이와 방향 모두에서 변화합니다. 중심 힘이 대략 역제곱 법칙이라면 벡터 A는 길이는 거의 일정하지만 방향은 천천히 회전합니다.[14] 일반화된 보존된 LRL A{\{\는 모든 중심 힘에 대해 정의될 수 있지만, 이 일반화된 벡터는 복잡한 위치 함수이며 일반적으로 닫힌 형태로 표현할 수 없습니다.[18][19]
LRL 벡터는 다음과 같은 특성에서 다른 보존된 양과 다릅니다. 일반적으로 보존된 양의 경우 시스템의 3차원 라그랑지안에 해당하는 순환 좌표가 있지만 LRL 벡터에 대한 해당 좌표는 존재하지 않습니다. 따라서 LRL 벡터의 보존은 예를 들어 아래에 설명된 바와 같이 포아송 괄호의 방법으로 직접 유도되어야 합니다. 이러한 종류의 보존된 양은 각운동량과 같은 일반적인 "기하학" 보존 법칙과 대조적으로 "동역학"이라고 불립니다.
재발견의 역사
LRL 벡터 A는 케플러 문제의 운동 상수로 행성과 쌍성의 운동 등 천문학적 궤도를 설명하는 데 유용합니다. 그럼에도 불구하고, 이것은 물리학자들 사이에서 잘 알려진 적이 없는데, 아마도 운동량과 각운동량보다 직관적이지 않기 때문일 것입니다. 그 결과 지난 3세기 동안 여러 차례 독립적으로 재발견되었습니다.[15]
야콥 헤르만은 A가 역제곱 중심 힘의 특별한 경우에 보존된다는 것을 처음으로 보여주었고,[22] 궤도 타원의 이심률과의 연관성을 밝혀냈습니다. 헤르만의 작품은 1710년 요한 베르누이에 의해 현대적인 형태로 일반화되었습니다.[23] 세기 말에 피에르시몽 드 라플라스는 A의 보존을 재발견하여 기하학적이 아니라 해석적으로 유도했습니다.[24] 19세기 중반에 William Rowan Hamilton은 아래에 정의된 등가 이심률 벡터를 [16]유도하여 운동량 벡터 p가 역제곱 중심 힘 하에서 원 위에서 운동한다는 것을 보여주었습니다(그림 3).[12]
20세기 초에 Josiah Willard Gibbs는 벡터 분석을 통해 동일한 벡터를 도출했습니다.[25] 깁스의 유도는 독일의 유명한 벡터 교과서에서 칼 룬지에 의해 예시로 사용되었으며,[26] 이는 빌헬름 렌츠에 의해 수소 원자의 양자역학적 처리에 대한 그의 논문에서 참조되었습니다.[27] 1926년 볼프강 파울리는 LRL 벡터를 이용하여 양자역학의 행렬역학 공식을 이용하여 수소 원자의 에너지 준위를 도출하였고,[7] 그 후 주로 룽지-렌츠 벡터로 알려지게 되었습니다.[15]
수학적 정의
단일 입자에 작용하는 역제곱 중심력은 다음 식에 의해 설명됩니다.
LRL 벡터 A는 수학적으로[1] 공식으로 정의됩니다.
어디에
- m은 중심 힘 아래에서 움직이는 점입자의 질량입니다.
- p는 운동량 벡터이고,
- L = r × p는 각운동량 벡터입니다.
- r은 입자의 위치 벡터(그림 1),
- 은 해당 단위 벡터, r =r \mathbf {\ha {r}} = {\frac {\mathbf {r}} {r}, 그리고
- r은 힘의 중심으로부터 질량의 거리인 r의 크기입니다.
LRL 벡터의 SI 단위는 줄 킬로그램 미터(J ⋅kg ⋅m)입니다. 이는 p와 L의 단위가 각각 kg ⋅m/s와 J ⋅이기 때문입니다. 이는 m(kg) 및 k(N ⋅m)의 단위와 일치합니다.
LRL 벡터 A의 이 정의는 고정된 힘의 작용 하에서 움직이는 질량 m의 단일 점 입자에 관한 것입니다. 그러나 동일한 정의는 m을 두 물체의 감소된 질량으로, r을 두 물체 사이의 벡터로 사용함으로써 케플러 문제와 같은 두 물체 문제로 확장될 수 있습니다.
가정된 힘은 보수적이므로 총 에너지 E는 운동 상수입니다.
가정된 힘도 중심 힘입니다. 따라서 각운동량 벡터 L도 보존되어 입자가 이동하는 평면을 정의합니다. LRL 벡터 A는 p × L과 r이 모두 L에 수직이므로 각운동량 벡터 L에 수직입니다. 그 결과 A는 운동면에 놓여 있습니다.
동일한 운동 상수에 대한 대체 공식은 일반적으로 질량 m, 힘 매개변수 k 또는 각운동량 L과 같은 상수로 벡터를 스케일링함으로써 정의될 수 있습니다.[15] 가장 일반적인 변형은 A를 mk로 나누는 것인데,[2][16] 이는 모듈러스가 원뿔의 이심률과 동일한 반장축을 따른 무차원 벡터입니다.
케플러 궤도의 유도

궤도의 모양과 방향은 다음과 같이 LRL 벡터로부터 알 수 있습니다.[1] 위치 벡터 r과 함께 A의 점 곱을 취하면 다음과 같은 식을 얻을 수 있습니다.
케플러 방정식의 해를 재배열하면
이는 편심 e의 원뿔 단면에 대한 공식에 해당합니다.
그 자체로 A의 점 곱을 취하면 총 에너지 E를 포함하는 방정식이 생성됩니다.[1]
따라서 에너지 E가 음(결합 궤도)이면 이심률은 1보다 작으며 궤도는 타원입니다. 반대로 에너지가 양이면 이심률은 1보다 크고 궤도는 쌍곡선입니다.[1][1] 마지막으로 에너지가 정확히 0이면 이심률은 1이고 궤도는 포물선입니다.[1] 모든 경우에 A의 방향은 원뿔 단면의 대칭축을 따라 있으며 힘의 중심에서 가장 가까운 접근 지점인 근일점을 향합니다.[1]
원운동량 호도그래프

LRL 벡터 A와 각운동량 벡터 L의 보존은 운동량 벡터 p가 역제곱 중심 힘 하에서 원 위를 이동한다는 것을 보여주는 데 유용합니다.[12][15]
도트 곱하기
z축을 따라 L을 선택하고 장축을 x축으로 선택하면 p에 대한 로커스 방정식이 생성됩니다.
즉, 운동량 벡터 p는 (0, A/L)을 중심으로 하는 반지름 mk/L = L/ ℓ의 원에 국한됩니다. 유계 궤도의 경우, 이심률 e는 그림 3과 같은 각도 η의 코사인에 해당합니다. 무한궤도의 경우 > m > 가 있으므로 -축과 교차하지 않습니다.
원형 궤도의 축퇴 한계에서 A가 사라지면 원의 중심은 원점(0,0)에 있습니다. 간결성을 위해 p = {\textstyle p_{0} = {\sqrt {2m E}}를 도입하는 것도 유용합니다.
이 원형 호도그래프는 케플러 문제의 대칭성을 설명하는 데 유용합니다.
운동 상수와 초적분성
7개의 스칼라 양 E, A 및 L(벡터가 되며 후자의 두 개는 각각 3개의 보존된 양을 제공함)은 A ⋅ L = 0 및 A = mk + 2 mEL의 두 방정식으로 관련되어 5개의 독립적인 운동 상수를 제공합니다. (A의 크기, 따라서 궤도의 이심률 e는 총 각운동량 L과 에너지 E로부터 결정될 수 있기 때문에 A의 방향만 독립적으로 보존됩니다. 게다가 A는 L과 수직이어야 하기 때문에 추가적으로 보존된 양 하나만 기여합니다.)
이것은 초기 시간이 운동 상수에 의해 결정되지 않기 때문에 입자의 궤도를 지정하는 6개의 초기 조건(각각 3개의 성분이 있는 입자의 초기 위치 및 속도 벡터)과 일치합니다. 따라서 6차원 위상 공간에서 생성되는 1차원 궤도는 완전히 지정됩니다.
자유도가 d인 기계 시스템은 2d의 초기 조건이 있고 초기 시간은 운동 상수로 결정될 수 없기 때문에 최대 2d - 1의 운동 상수를 가질 수 있습니다. 운동 상수가 d 이상인 계를 초적분이라 하고, 상수가 2 - 1인 계를 최대 초적분이라 합니다.[30] 하나의 좌표계에서 해밀턴-야코비 방정식의 해는 d개의 운동 상수만을 산출할 수 있기 때문에, 초적분 시스템은 둘 이상의 좌표계에서 분리 가능해야 합니다.[31] 케플러 문제는 3개의 자유도(d = 3)와 5개의 독립적인 운동 상수를 가지므로 최대로 초적분이 가능합니다. 해밀턴-야코비 방정식은 아래에 설명된 대로 구면 좌표와 포물선 좌표 모두에서 분리할 수 있습니다.
궤도는 운동 상수의 위상 공간 등면의 교차점이기 때문에 최대 초적분 시스템은 위상 공간에서 닫힌 1차원 궤도를 따릅니다. 결과적으로 궤도는 이 특정 문제에서 5개의 이 모든 독립적인 등면의 모든 구배에 수직이므로 이 모든 구배의 일반화된 교차 곱에 의해 결정됩니다. 결과적으로 모든 초적분 시스템은 해밀턴 역학과 마찬가지로 [32]남부 역학에 의해 자동적으로 기술될 수 있습니다.
최대로 초적분 가능한 시스템은 아래 그림과 같이 정류 관계를 사용하여 양자화할 수 있습니다.[33] 그럼에도 불구하고, 이와 동등하게, 이 고전적인 케플러 문제가 양자 수소 원자에 들어가는 것과 같은 남부 프레임워크에서도 양자화됩니다.[34]
교란 전위 하에서의 진화

라플라스-룽지-렌츠 벡터 A는 완벽한 역제곱 중심 힘에 대해서만 보존됩니다. 그러나 행성 운동과 같은 대부분의 실제 문제에서 두 물체 사이의 상호 작용 위치 에너지는 정확히 역제곱 법칙이 아니라 위치 에너지 h(r)에 의해 설명되는 소위 섭동이라는 추가 중심 힘을 포함할 수 있습니다. 이러한 경우, LRL 벡터는 궤도의 평면에서 느리게 회전하며, 이는 궤도의 느린 아피달 세차에 해당합니다.
가정에 따르면 퍼터빙 퍼텐셜 h(r)는 보존 중심 힘이며, 이는 총 에너지 E와 각운동량 벡터 L이 보존됨을 의미합니다. 따라서, 운동은 여전히 L에 수직인 평면에 놓여 있고 A = mk + 2mEL 방정식으로부터 A 크기가 보존됩니다. 섭동 포텐셜 h(r)는 어떤 종류의 함수일 수 있지만, 두 물체 사이의 주요 역제곱 힘보다 상당히 약해야 합니다.
LRL 벡터가 회전하는 속도는 퍼터빙 퍼텐셜 h(r)에 대한 정보를 제공합니다. 표준 섭동 이론과 작용각 좌표를 사용하면 A가 다음과 같은 속도로 회전한다는 것을 쉽게[1] 알 수 있습니다.
이 접근법은 정상적인 뉴턴 중력 퍼텐셜에 작은 효과적인 역-입방 섭동을 추가하는 아인슈타인의 일반 상대성 이론을 검증하는 데 도움을 주기 위해 사용되었습니다.[35]
적분에 이 함수를 삽입하고 방정식을 사용합니다.
포아송 대괄호
확장되지 않은 함수
문제의 대수적 구조는 이후 절에서 설명한 바와 같이 SO(42)/Z ~ SO(3) × SO(3)입니다.[11] 각운동량 벡터 L의 세 성분 L은i 포아송 대괄호를[1] 갖습니다.
마지막으로, L과 A는 모두 운동 상수이므로, 우리는
포아송 괄호는 다음 섹션에서 양자 기계적 정류 관계로 확장되고 다음 섹션에서는 Lie 괄호로 확장됩니다.
축척된 함수
아래에 언급된 바와 같이, 스케일된 라플라스-룽지-렌츠 벡터 D는 A를 = 2 p_{0} = {\H}}로 나누어 각운동량과 동일한 단위로 정의될 수 있습니다 D는 여전히 벡터처럼 변환되기 때문에 각운동량 벡터 L을 가진 D의 포아송 괄호는 유사한 형태로 작성될 수 있습니다.
자체가 있는 D의 포아송 괄호는 H의 부호, 즉 에너지가 음(역제곱 중심력 아래에서 닫힌 타원 궤도를 생성함)인지 양(역제곱 중심력 아래에서 열린 쌍곡 궤도를 생성함)인지에 따라 달라집니다. 음의 에너지(예: 바인딩된 시스템의 경우)의 경우 포아송 대괄호는[42]
반대로 양의 에너지의 경우 포아송 대괄호는 반대의 부호를 갖습니다.
양의 에너지와 음의 에너지의 구별은 스케일링된 LRL 벡터의 구성 요소 간의 포아송 괄호 관계의 오른쪽에서 해밀턴을 제거하는 스케일링이 해밀턴의 제곱근을 포함하기 때문에 발생합니다. 실제 값 함수를 얻으려면 양의 값( = H H = 과 음의 값(H = - H {\displaystyle H = - H})을 구별하는 해밀턴의 절대 값을 취해야 합니다.
운동량공간에서 수소원자에 대한 라플라스-룽게-렌츠 연산자
최근에 모멘텀 공간에서 스케일된 라플라스-룽지-렌츠 연산자가 발견되었습니다.[44][45] 연산자의 공식은 위치 공간보다 단순합니다.
여기서 "도수 연산자"
동차 다항식에 차수를 곱합니다.
카시미르 불변량과 에너지 준위
음의 에너지에 대한 카시미르 불변량은
D와 L의 모든 성분을 가진 사라지는 포아송 대괄호를 갖습니다.
그러나 다른 불변인 C는1 사소하지 않고 m, k 및 E에만 의존합니다. 표준 양자화 시, 이 불변성은 슈뢰딩거 방정식의 기존 솔루션 대신 양자역학적 표준 정류 관계만을 사용하여 수소 유사 원자의 에너지 수준을 도출할 수 있게 합니다.[8][43] 이 파생은 다음 섹션에서 자세히 설명합니다.
수소 원자의 양자역학
포아송 괄호는 대부분의 고전적 시스템을 양자화하기 위한 간단한 지침을 제공합니다. 두 양자 역학 연산자의 절단 관계는 해당 고전적 변수의 포아송 괄호에 i ħ을 곱하여 지정됩니다.
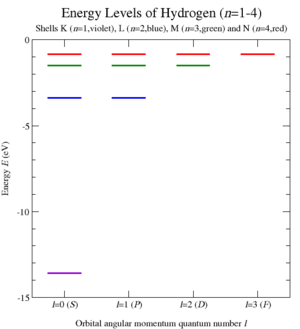
이 양자화를 수행하고 케플러 문제에 대한1 C 카시미르 연산자의 고유값을 계산함으로써 볼프강 파울리는 수소와 유사한 원자의 에너지 수준을 도출할 수 있었고(그림 6), 따라서 원자 방출 스펙트럼을 도출할 수 있었습니다.[7] 이 우아한 1926년의 유도는 슈뢰딩거 방정식이 개발되기 전에 얻어졌습니다.[47]
LRL 벡터 A에 대한 양자 역학 연산자의 미묘한 점은 운동량과 각운동량 연산자가 통근하지 않는다는 것입니다. 따라서 p와 L의 양자 연산자 교차 곱은 신중하게 정의되어야 합니다.[8] 일반적으로 데카르트 성분 A에s 대한 연산자는 대칭화된 (헤르미트) 곱을 사용하여 정의됩니다.
이 연산자들로부터 L에 대한 추가 사다리 연산자를 정의할 수 있습니다.
정규화된 첫 번째 카시미르 불변 연산자, 위의 양자 유사체도 마찬가지로 정의할 수 있습니다.
이 사다리 연산자를 총 각운동량의 고유 상태 ℓm 〉에 적용하면 첫 번째 카시미르 연산자 C의 고유값이 n - 1로 양자화된 것으로 보입니다. 중요한 것은 C가 사라짐으로써 ℓ와 m개의 양자수에 독립적으로 에너지 준위가 퇴화된다는 것입니다.
따라서 에너지 수준은 다음과 같습니다.
보존과 대칭
LRL 벡터의 보존은 시스템의 미묘한 대칭에 해당합니다. 고전역학에서 대칭은 계의 에너지를 변화시키지 않고 한 궤도를 다른 궤도에 매핑하는 연속적인 작업이며, 양자역학에서 대칭은 동일한 에너지의 전자 궤도를 "혼합"하는 연속적인 작업, 즉 퇴화된 에너지 수준입니다. 보존된 양은 일반적으로 이러한 대칭과 관련이 있습니다.[1] 예를 들어, 모든 중심 힘은 회전 그룹 SO(3) 아래에서 대칭이므로 각운동량 L이 보존됩니다. 고전적으로 시스템의 전체 회전은 궤도의 에너지에 영향을 미치지 않습니다. 양자역학적으로 회전은 에너지를 변화시키지 않고 동일한 양자수 ℓ의 구면 고조파를 혼합합니다.

역제곱 중심 힘의 대칭성은 더 높고 더 미묘합니다. 케플러 문제의 독특한 대칭성은 각운동량 벡터 L과 LRL 벡터 A(위에서 정의한 바와 같이)를 보존하고 양자역학적으로 수소의 에너지 수준이 각운동량 양자수 ℓ 및 m에 의존하지 않도록 보장합니다. 그러나 대칭 작업이 더 높은 차원의 공간에서 이루어져야 하기 때문에 대칭성은 더 미묘합니다. 그러한 대칭은 종종 "숨겨진 대칭"이라고 불립니다.[51]
고전적으로 케플러 문제의 더 높은 대칭성은 에너지는 보존하지만 각운동량은 보존하지 않는 궤도의 연속적인 변경을 가능하게 합니다. 즉, 에너지는 같지만 각운동량(이심도)이 다른 궤도는 연속적으로 서로 변환될 수 있습니다. 양자역학적으로 이는 s(ℓ =0)와 p(ℓ =1) 원자 궤도와 같이 ℓ와 m개의 양자수가 다른 궤도를 혼합하는 것에 해당합니다. 이러한 혼합은 일반적인 3차원 번역이나 회전으로는 이루어질 수 없으며, 더 높은 차원의 회전과 동등합니다.
음의 에너지 - 즉, 결합된 시스템의 경우 더 높은 대칭 그룹은 4차원 벡터의 길이를 보존하는 SO(4)입니다.
1935년 블라디미르 포크는 양자역학적 결합 케플러 문제가 4차원 공간의 3차원 단위 구에 국한된 자유 입자의 문제와 동등하다는 것을 보여주었습니다.[10] 구체적으로, Fock은 케플러 문제에 대한 운동량 공간에서의 슈뢰딩거 파동 함수가 구면에 구면 고조파의 입체 투영임을 보여주었습니다. 구의 회전과 재투영은 에너지를 변경하지 않고 타원 궤도의 연속적인 매핑을 초래하며, SO(4) 대칭은 때로는 포크 대칭으로 알려져 있으며,[52] 양자역학적으로 이는 동일한 에너지 양자수 n의 모든 궤도의 혼합에 해당합니다. Valentine Bargmann은 이후 각운동량 벡터 L과 스케일링된 LRL 벡터 A에 대한 포아송 괄호가 SO(4)에 대한 Lie 대수를 형성한다고 언급했습니다.[11][42] 간단히 말해서, 6개의 양 A와 L은 4차원에서 보존된 6개의 각운동량에 해당하며, 그 공간에서 가능한 6개의 단순 회전과 관련이 있습니다(4개에서 2개의 축을 선택하는 6가지 방법이 있습니다). 이 결론은 우리의 우주가 3차원 구라는 것을 의미하는 것이 아니라, 단지 이 특정한 물리 문제(역제곱 중심력에 대한 2체 문제)가 3차원 구 위의 자유 입자와 수학적으로 동등하다는 것을 의미합니다.
양의 에너지(즉, 결합되지 않은 "산란된" 시스템의 경우, 더 높은 대칭 그룹은 SO(3,1)이며, 이는 4-벡터의 민코프스키 길이를 보존합니다.
음의[10] 에너지와 양의[11] 에너지 사례는 모두 Fock과 Bargmann에 의해 고려되었으며 Bander와 Itzykson에 의해 백과사전적으로 검토되었습니다.[53][54]
중심 힘계의 궤도들, 특히 케플러 문제의 궤도들 또한 반사 하에서 대칭입니다. 따라서 위에서 언급한 SO(3), SO(4) 및 SO(3,1) 그룹은 궤도의 완전한 대칭 그룹이 아닙니다. 완전한 그룹은 각각 O(3), O(4) 및 O(3,1)입니다. 그럼에도 불구하고 각운동량과 LRL 벡터의 보존을 입증하려면 연결된 하위 그룹인 SO(3), SO(4) 및 SO(3+,1)만 필요합니다. 반사 대칭은 그룹의 Lie 대수에서 파생될 수 있는 보존과 무관합니다.
4차원 회전 대칭

케플러 문제와 4차원 회전 대칭 SO(4) 사이의 연결을 쉽게 시각화할 수 있습니다.[53][55][56] 4차원 직각좌표를 (w, x, y, z)라고 표기하면 (x, y, z)는 정규 위치 벡터 r의 직각좌표를 나타냅니다. 3차원 운동량 벡터 p는 3차원 단위 구의 4차원 벡터η {\displaystyle {\eta}}와 연관되어 있습니다.
여기서 은 새로운 w축을 따른 단위 벡터입니다. 변환 매핑 p를 η로 고유하게 반전시킬 수 있습니다. 예를 들어, 운동량의 x 성분은 다음과 같습니다.
일반성을 잃지 않고 z축이 각운동량 벡터 L과 정렬되고 운동량 호도그래프가 그림 7과 같이 y축에 원의 중심을 두고 정렬되도록 직각좌표를 선택하여 정상적인 회전 대칭을 제거할 수 있습니다. 움직임은 평면이고 p와 L은 수직이므로 p = η = 0이며 주의력은 3차원 벡터 η = (η w, η x, η y) {\displaystyle {\boldsymbol {\eta}} = (\eta _{w},\eta _{x},\eta _{y입니다. 아폴론적 운동량 호도그래프 계열(그림 7)은 3차원ηdisplaystyle {\eta}} 구에 있는 대원 계열에 해당하며, 모두 두 초점 η = ±1에서 η 축과 교차하며 p = ±p에서 운동량 호도그래프 초점에 해당합니다. 이 거대한 원들은 η 축을 중심으로 간단한 회전으로 연관되어 있습니다(그림 8). 이 회전 대칭은 동일한 에너지의 궤도를 모두 서로 변환하지만, 이러한 회전은 4차원 η을 변환하기 때문에 일반적인 3차원 회전과 직교합니다. 이 더 높은 대칭성은 케플러 문제의 특징이며 LRL 벡터의 보존에 해당합니다.
케플러 문제에 대한 우아한 작용각 변수 솔루션은 타원형 원통 좌표(χ, ψ, φ)를 선호하는 중복 4차원 좌표η displaystyle {\eta}}를 제거하여 얻을 수 있습니다.
다른 퍼텐셜과 상대성 이론에 대한 일반화
Laplace-Runge-Lenz 벡터는 또한 다른 상황에 적용되는 보존된 양을 식별하기 위해 일반화될 수 있습니다.
균일한 전기장 E가 존재하는 경우, 일반화된 라플라스-룽지-렌츠 벡터 는[17][58]
라플라스-룽지-렌츠 벡터를 다른 퍼텐셜과 특수 상대성 이론에 더 일반화하면, 가장 일반적인 형태는 다음과[18] 같이 쓸 수 있습니다.
여기서 u = 1/r 및 ξ = cos θ이며, 각도 θ는 다음과 같이 정의됩니다.
그리고 γ은 로런츠 인자입니다. 이전과 같이 보존된 각운동량 벡터와 교차곱을 취하면 보존된 이항정규벡터 B를 얻을 수 있습니다.
이 두 벡터는 마찬가지로 보존된 다이아딕 텐서 W로 결합될 수 있습니다.
그림에서 비상대론적 등방성 고조파 발진기에 대한 LRL 벡터를 계산할 수 있습니다.[18] 힘이 중심이 되니까,
보존된 다이아딕 텐서는 간단한 형태로 쓸 수 있습니다.
대응하는 룽지-렌츠 벡터는 더 복잡합니다.
Laplace-Runge-Lenz 벡터가 케플러 문제에서 보존된다는 증명
다음은 역제곱 법칙을 따르는 중심 힘 하에서 LRL 벡터가 보존된다는 것을 보여주는 논법입니다.
보존의 직접증명
입자에 작용하는 중심 힘 는
반지름 의 함수 f f에 대해 L = × displaystyle {L =\mathbf {r} \times \mathbf {p} }는 중심 힘 아래에 보존되므로, d t L = 0 {\textstyle {\frac {dt}}\mathbf {L} = 0} 및
여기서 운동량 = d r {\textstyle \mathbf {p} = m{\frac {d\mathbf {r} {dt}}이고 라그랑주 공식을 사용하여 삼중 교차 곱을 단순화한 경우
아이덴티티
등식이 나오다
역제곱 중심 f =- 2 {\textstyle f(r) = {\frac {-k}{r^{2}}의 특별한 경우, 이는 다음과 같습니다.
따라서 A는 역제곱 중심[59] 힘에 대해 보존됩니다.
각운동량과 각속도의 관계를 사용하면 더 짧은 증명을 얻을 수 있습니다. = 2ω displaystyle {L} = mr^{2} {\boldsymbol {\omega}}. L {\displaystyle \mathbf {L} }에 수직인 평면으로 이동하는 입자에 대해 유지됩니다. 역제곱 중심력에 대해 지정하면, × 의 시간 도함수는
이 기사의 다른 곳에서 설명한 바와 같이, 이 LRL 벡터 A는 모든 중심 힘에 대해 정의할 수 있는 일반 보존 A{\{\의 특별한 경우입니다.[18][19] 그러나 대부분의 중심 힘은 닫힌 궤도를 생성하지 않기 때문에(베르트랑의 정리 참조) 유사 A 는 단순한 정의가 거의 없으며 일반적으로r과 A {A}} 의 각도 θ의 다중 값 함수입니다.
포물선 좌표의 해밀턴-야코비 방정식
LRL 벡터의 일정성은 포물선 좌표(ξ, η)의 해밀턴-야코비 방정식에서도 유도될 수 있으며, 이 방정식은 다음과 같이 정의됩니다.
이 좌표들의 반전은
이 좌표에서 해밀턴-야코비 방정식의 분리는 두 등가 방정식을[17][60] 산출합니다.
노터 정리
위에서 설명한 회전 대칭과 LRL 벡터의 보존 사이의 연결은 Noether의 정리를 통해 정량적으로 이루어질 수 있습니다. 운동 상수를 찾는 데 사용되는 이 정리는 물리계의 일반화 좌표의 무한히 작은 변화를 의미합니다.
그것은 라그랑지안이 총 시간 도함수에 의해 1차로 변화하게 하는 원인이 됩니다.
보존된 수량 γ에 해당합니다.
특히 보존된 LRL 벡터 성분 A는s 좌표의[61] 변화에 해당합니다.
여기서 i는 1, 2, 3이고, x와 p는 각각 위치와 운동량 벡터 r과 p의 i번째 성분이며, δ는 평소와 같이 크로네커 델타를 나타냅니다. 결과적으로 라그랑지안의 1차 변화는
보존된 양 γ에 대한 일반 공식으로 대체하면 LRL 벡터의 보존된 성분 A가 산출됩니다.
거짓말 변환

LRL 벡터 A의 보존에 대한 노에테르의 정리 유도는 훌륭하지만 한 가지 단점이 있습니다: 좌표 변화 δx는 위치 r뿐만 아니라 운동량 p 또는 동등하게 속도 v도 포함합니다. 이 단점은 Sophus Lie가 개척한 접근법을 사용하여 A의 보존을 유도함으로써 제거될 수 있습니다.[63][64] 구체적으로, 좌표 r과 시간 t가 파라미터 λ의 서로 다른 파워에 의해 스케일링되는 Lie 변환을 정의할 수 있습니다(그림 9).
이 변환은 총 각운동량 L과 에너지 E를 변화시킵니다.
반음영이 전역 스케일링에 의해 변경되지 않기 때문에 A의 방향도 보존됩니다. 이 변환은 또한 케플러의 세 번째 법칙, 즉 반축 a와 주기 T가 일정한2 T/a를3 형성한다는 것을 보존합니다.
대체 척도, 기호 및 공식
운동량 및 각운동량 벡터 p와 L과 달리, 라플라스-룽지-렌츠 벡터에 대한 보편적으로 인정되는 정의는 없습니다. 몇몇 다른 스케일링 인자와 기호들이 과학 문헌에서 사용됩니다. 가장 일반적인 정의는 위에 나와 있지만 다른 일반적인 대안은 무차원 보존 이심률 벡터를 얻기 위해 양 mk로 나누는 것입니다.
여기서 v는 속도 벡터입니다. 이 축척된 벡터 e는 A와 같은 방향을 가지며 크기는 궤도의 이심률과 같으므로 원형 궤도에서는 사라집니다.
예를 들어 A를 m으로 단독 분할하는 등 다른 스케일 버전도 가능합니다.
드물게 LRL 벡터의 부호가 반대로, 즉 -1로 스케일링될 수 있습니다. LRL 벡터의 다른 일반적인 기호로는 a, R, F, J 및 V가 있습니다. 그러나 LRL 벡터의 스케일링 및 심볼 선택은 보존에 영향을 미치지 않습니다.

대안적인 보존 벡터는 William Rowan Hamilton이 연구한 이항정규 벡터 B입니다.[16]
보존되고 타원의 작은 반축을 따라 위치합니다. (이심성이 사라지는 것에 대해서는 정의되지 않았습니다.)
LRL 벡터 A = B × L은 B와 L의 교차 곱입니다(그림 4). 위의 해당 부분의 운동량 호도그래프에서, B는 운동량의 원점과 원형 호도그래프의 중심을 연결하고, 크기 A/L을 갖는 것을 쉽게 볼 수 있습니다. 근일점에서, 그것은 운동량의 방향을 가리킵니다.
벡터 B는 A와 L에 모두 수직이므로 "이항정규"로 표시됩니다. 이진 정규 벡터는 LRL 벡터 자체와 마찬가지로 다양한 스케일과 기호로 정의할 수 있습니다.
두 개의 보존된 벡터 A와 B를 결합하여 보존된 다이애딕 텐서 W를 만들 수 있습니다.[18]
벡터 A와 B는 서로 수직이므로 보존된 텐서 W의 주요 축, 즉 크기가 조정된 고유 벡터로 볼 수 있습니다. W는 L에 수직이고,
좀 더 직접적으로, 이 방정식은 명시적인 구성 요소에서,
참고 항목
참고문헌
- ^ a b c d e f g h i j k l m n o Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison Wesley. pp. 102–105, 421–422.
- ^ a b c Taff, L. G. (1985). Celestial Mechanics: A Computational Guide for the Practitioner. New York: John Wiley and Sons. pp. 42–43.
- ^ Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison Wesley. pp. 94–102.
- ^ Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics (2nd ed.). New York: Springer-Verlag. p. 38. ISBN 0-387-96890-3.
- ^ Sommerfeld, A. (1964). Mechanics. Lectures on Theoretical Physics. Vol. 1. Translated by Martin O. Stern (4th ed.). New York: Academic Press. pp. 38–45.
- ^ Lanczos, C. (1970). The Variational Principles of Mechanics (4th ed.). New York: Dover Publications. pp. 118, 129, 242, 248.
- ^ a b c Pauli, W. (1926). "Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik. 36 (5): 336–363. Bibcode:1926ZPhy...36..336P. doi:10.1007/BF01450175. S2CID 128132824.
- ^ a b c d e f Bohm, A. (1993). Quantum Mechanics: Foundations and Applications (3rd ed.). New York: Springer-Verlag. pp. 205–222.
- ^ Hanca, J.; Tulejab, S.; Hancova, M. (2004). "Symmetries and conservation laws: Consequences of Noether's theorem". American Journal of Physics. 72 (4): 428–35. Bibcode:2004AmJPh..72..428H. doi:10.1119/1.1591764.
- ^ a b c Fock, V. (1935). "Zur Theorie des Wasserstoffatoms". Zeitschrift für Physik. 98 (3–4): 145–154. Bibcode:1935ZPhy...98..145F. doi:10.1007/BF01336904. S2CID 123112334.
- ^ a b c d e Bargmann, V. (1936). "Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock". Zeitschrift für Physik. 99 (7–8): 576–582. Bibcode:1936ZPhy...99..576B. doi:10.1007/BF01338811. S2CID 117461194.
- ^ a b c Hamilton, W. R. (1847). "The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction". Proceedings of the Royal Irish Academy. 3: 344–353.
- ^ Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison Wesley. p. 421.
- ^ a b c d Arnold, V. I. (1989). Mathematical Methods of Classical Mechanics (2nd ed.). New York: Springer-Verlag. pp. 413–415. ISBN 0-387-96890-3.
- ^ a b c d e f g Goldstein, H. (1975). "Prehistory of the Runge–Lenz vector". American Journal of Physics. 43 (8): 737–738. Bibcode:1975AmJPh..43..737G. doi:10.1119/1.9745.
Goldstein, H. (1976). "More on the prehistory of the Runge–Lenz vector". American Journal of Physics. 44 (11): 1123–1124. Bibcode:1976AmJPh..44.1123G. doi:10.1119/1.10202. - ^ a b c d Hamilton, W. R. (1847). "Applications of Quaternions to Some Dynamical Questions". Proceedings of the Royal Irish Academy. 3: Appendix III.
- ^ a b c d Landau, L. D.; Lifshitz E. M. (1976). Mechanics (3rd ed.). Pergamon Press. p. 154. ISBN 0-08-021022-8.
- ^ a b c d e f Fradkin, D. M. (1967). "Existence of the Dynamic Symmetries O4 and SU3 for All Classical Central Potential Problems". Progress of Theoretical Physics. 37 (5): 798–812. Bibcode:1967PThPh..37..798F. doi:10.1143/PTP.37.798.
- ^ a b c Yoshida, T. (1987). "Two methods of generalisation of the Laplace–Runge–Lenz vector". European Journal of Physics. 8 (4): 258–259. Bibcode:1987EJPh....8..258Y. doi:10.1088/0143-0807/8/4/005. S2CID 250843588.
- ^ a b Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison Wesley. pp. 1–11.
- ^ a b Symon, K. R. (1971). Mechanics (3rd ed.). Addison Wesley. pp. 103–109, 115–128.
- ^ Hermann, J. (1710). "Metodo d'investigare l'Orbite de' Pianeti, nell' ipotesi che le forze centrali o pure le gravità degli stessi Pianeti sono in ragione reciproca de' quadrati delle distanze, che i medesimi tengono dal Centro, a cui si dirigono le forze stesse". Giornale de Letterati d'Italia. 2: 447–467.
Hermann, J. (1710). "Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710". Histoire de l'Académie Royale des Sciences. 1732: 519–521. - ^ Bernoulli, J. (1710). "Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710". Histoire de l'Académie Royale des Sciences. 1732: 521–544.
- ^ Laplace, P. S. (1799). Traité de mécanique celeste. Paris, Duprat. Tome I, Premiere Partie, Livre II, pp.165ff.
- ^ Gibbs, J. W.; Wilson E. B. (1901). Vector Analysis. New York: Scribners. p. 135.
- ^ Runge, C. (1919). Vektoranalysis. Vol. I. Leipzig: Hirzel.
- ^ Lenz, W. (1924). "Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung". Zeitschrift für Physik. 24 (1): 197–207. Bibcode:1924ZPhy...24..197L. doi:10.1007/BF01327245. S2CID 121552327.
- ^ Symon, K. R. (1971). Mechanics (3rd ed.). Addison Wesley. pp. 130–131.
- ^ 보존된 이진 정규 해밀턴 벡터 ≡ × / L2 {B {L / L^{2}} 이 운동량 평면(분홍색)에서 더 단순한 기하학적 의미를 가지며 = B × L {= {B} \times \mathbf {L}, 파테라 참조, R. P. (1981). "Rungge-Lenz 벡터의 모멘트-공간 유도", Am. J. Phys 49593–594. 길이가 A/L이며 섹션 #대체 스케일링, 기호 및 공식에 설명되어 있습니다.
- ^ Evans, N. W. (1990). "Superintegrability in classical mechanics". Physical Review A. 41 (10): 5666–5676. Bibcode:1990PhRvA..41.5666E. doi:10.1103/PhysRevA.41.5666. PMID 9902953.
- ^ Sommerfeld, A. (1923). Atomic Structure and Spectral Lines. London: Methuen. p. 118.
- ^ Curtright, T.; Zachos C. (2003). "Classical and Quantum Nambu Mechanics". Physical Review. D68 (8): 085001. arXiv:hep-th/0212267. Bibcode:2003PhRvD..68h5001C. doi:10.1103/PhysRevD.68.085001. S2CID 17388447.
- ^ Evans, N. W. (1991). "Group theory of the Smorodinsky–Winternitz system". Journal of Mathematical Physics. 32 (12): 3369–3375. Bibcode:1991JMP....32.3369E. doi:10.1063/1.529449.
- ^ Zachos, C.; Curtright T. (2004). "Branes, quantum Nambu brackets, and the hydrogen atom". Czech Journal of Physics. 54 (11): 1393–1398. arXiv:math-ph/0408012. Bibcode:2004CzJPh..54.1393Z. doi:10.1007/s10582-004-9807-x. S2CID 14074249.
- ^ a b Einstein, A. (1915). "Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie". Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1915: 831–839. Bibcode:1915SPAW.......831E.
- ^ Le Verrier, U. J. J. (1859). "Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète". Comptes Rendus de l'Académie des Sciences de Paris. 49: 379–383.
- ^ Will, C. M. (1979). General Relativity, an Einstein Century Survey (SW Hawking and W Israel ed.). Cambridge: Cambridge University Press. Chapter 2.
- ^ Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press.
- ^ Roseveare, N. T. (1982). Mercury's Perihelion from Le Verrier to Einstein. Oxford University Press. ISBN 978-0-19-858174-1.
- ^ Hall 2013 Proposition 17.25.
- ^ Hall 2013 Proposition 18.7; Hall은 LRL 벡터의 다른 정규화를 사용합니다.
- ^ a b 홀 2013 정리 18.9.
- ^ a b 2013관
- ^ Efimov, S.P. (2022). "Coordinate space modification of Fock's theory. Harmonic tensors in the quantum Coulomb problem". Physics-Uspekhi. 65 (9): 952–967. Bibcode:2022PhyU...65..952E. doi:10.3367/UFNe.2021.04.038966. S2CID 234871720.
- ^ Efimov, S.P. (2023). "Runge-Lenz Operator in the Momentum Space". JETP Letters. 117 (9): 716–720. Bibcode:2023JETPL.117..716E. doi:10.1134/S0021364023600635. S2CID 259225778.
- ^ Dirac, P. A. M. (1958). Principles of Quantum Mechanics (4th revised ed.). Oxford University Press.
- ^ Schrödinger, E. (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik. 384 (4): 361–376. Bibcode:1926AnP...384..361S. doi:10.1002/andp.19263840404.
- ^ Hall 2013 Proposition 18.12.
- ^ Merzbacher, Eugen (1998-01-07). Quantum Mechanics. John Wiley & Sons. pp. 268–270. ISBN 978-0-471-88702-7.
- ^ 홀 2013 정리 18.14.
- ^ a b Prince, G. E.; Eliezer C. J. (1981). "On the Lie symmetries of the classical Kepler problem". Journal of Physics A: Mathematical and General. 14 (3): 587–596. Bibcode:1981JPhA...14..587P. doi:10.1088/0305-4470/14/3/009.
- ^ Nikitin, A G (7 December 2012). "New exactly solvable systems with Fock symmetry". Journal of Physics A: Mathematical and Theoretical. 45 (48): 485204. arXiv:1205.3094. Bibcode:2012JPhA...45V5204N. doi:10.1088/1751-8113/45/48/485204. S2CID 119138270.
- ^ a b Bander, M.; Itzykson C. (1966). "Group Theory and the Hydrogen Atom (I)". Reviews of Modern Physics. 38 (2): 330–345. Bibcode:1966RvMP...38..330B. doi:10.1103/RevModPhys.38.330.
- ^ Bander, M.; Itzykson C. (1966). "Group Theory and the Hydrogen Atom (II)". Reviews of Modern Physics. 38 (2): 346–358. Bibcode:1966RvMP...38..346B. doi:10.1103/RevModPhys.38.346.
- ^ Rogers, H. H. (1973). "Symmetry transformations of the classical Kepler problem". Journal of Mathematical Physics. 14 (8): 1125–1129. Bibcode:1973JMP....14.1125R. doi:10.1063/1.1666448.
- ^ Guillemin, V.; Sternberg S. (1990). Variations on a Theme by Kepler. Vol. 42. American Mathematical Society Colloquium Publications. ISBN 0-8218-1042-1.
- ^ Lakshmanan, M.; Hasegawa H. (1984). "On the canonical equivalence of the Kepler problem in coordinate and momentum spaces". Journal of Physics A. 17 (16): L889–L893. Bibcode:1984JPhA...17L.889L. doi:10.1088/0305-4470/17/16/006.
- ^ Redmond, P. J. (1964). "Generalization of the Runge–Lenz Vector in the Presence of an Electric Field". Physical Review. 133 (5B): B1352–B1353. Bibcode:1964PhRv..133.1352R. doi:10.1103/PhysRev.133.B1352.
- ^ Hall 2013 Proposition 2.34.
- ^ Dulock, V. A.; McIntosh H. V. (1966). "On the Degeneracy of the Kepler Problem". Pacific Journal of Mathematics. 19: 39–55. doi:10.2140/pjm.1966.19.39.
- ^ Lévy-Leblond, J. M. (1971). "Conservation Laws for Gauge-Invariant Lagrangians in Classical Mechanics". American Journal of Physics. 39 (5): 502–506. Bibcode:1971AmJPh..39..502L. doi:10.1119/1.1986202.
- ^ Gonzalez-Gascon, F. (1977). "Notes on the symmetries of systems of differential equations". Journal of Mathematical Physics. 18 (9): 1763–1767. Bibcode:1977JMP....18.1763G. doi:10.1063/1.523486.
- ^ Lie, S. (1891). Vorlesungen über Differentialgleichungen. Leipzig: Teubner.
- ^ Ince, E. L. (1926). Ordinary Differential Equations. New York: Dover (1956 reprint). pp. 93–113.
더보기
- Baez, John (2008). "The Kepler Problem Revisited: The Laplace–Runge–Lenz Vector" (PDF). Retrieved 2021-05-31.
- Baez, John (2003). "Mysteries of the gravitational 2-body problem". Archived from the original on 2008-10-21. Retrieved 2004-12-11.
- Baez, John (2018). "Mysteries of the gravitational 2-body problem". Retrieved 2021-05-31. 이전 소스의 업데이트된 버전입니다.
- D'Eliseo, M. M. (2007). "The first-order orbital equation". American Journal of Physics. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. doi:10.1119/1.2432126.
- Hall, Brian C. (2013), Quantum Theory for Mathematicians, Graduate Texts in Mathematics, vol. 267, Springer, Bibcode:2013qtm..book.....H, ISBN 978-1461471158.
- Leach, P. G. L.; G. P. Flessas (2003). "Generalisations of the Laplace–Runge–Lenz vector". J. Nonlinear Math. Phys. 10 (3): 340–423. arXiv:math-ph/0403028. Bibcode:2003JNMP...10..340L. doi:10.2991/jnmp.2003.10.3.6. S2CID 73707398.
 수 있지만, 이 일반화된 벡터는 복잡한 위치 함수이며 일반적으로
수 있지만, 이 일반화된 벡터는 복잡한 위치 함수이며 일반적으로 
















![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial L}}\langle h(r)\rangle &={\frac {\partial }{\partial L}}\left\{{\frac {1}{T}}\int _{0}^{T}h(r)\,dt\right\}\\[1em]&={\frac {\partial }{\partial L}}\left\{{\frac {m}{L^{2}}}\int _{0}^{2\pi }r^{2}h(r)\,d\theta \right\},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f7c4b1e625655dbe8eb20fe5dc980716081163c)






 해밀토니안입니다. 마지막 관계의 오른쪽에
해밀토니안입니다. 마지막 관계의 오른쪽에 













![{\displaystyle {\begin{aligned}{\boldsymbol {\eta }}&={\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0}^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\[1em]&={\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\mathbf {p} ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f8d97429200681d94a0a567c9409718a4718f9e)
 새로운
새로운 
![{\displaystyle {\begin{aligned}\eta _{w}&=\operatorname {cn} \chi \operatorname {cn} \psi ,\\[1ex]\eta _{x}&=\operatorname {sn} \chi \operatorname {dn} \psi \cos \phi ,\\[1ex]\eta _{y}&=\operatorname {sn} \chi \operatorname {dn} \psi \sin \phi ,\\[1ex]\eta _{z}&=\operatorname {dn} \chi \operatorname {sn} \psi ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/391a4c91a8ccea0624ed71aa768d70a302bbdda4)
![{\displaystyle {\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \right)\times \mathbf {r} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20af66a19dc9936aa349110ad731be096a79f881)
![{\displaystyle {\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \right)+\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\right)\right]L^{2}\mathbf {\hat {r}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b25780c204c1fbf553309e68374af2e32c721c9)










![{\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)={\frac {d\mathbf {p} }{dt}}\times \mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\right)=f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\right)-r^{2}{\frac {d\mathbf {r} }{dt}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1794709ea896ac78d1edaef3d279f9dab3670758)


![{\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \right)=-mf(r)r^{2}\left[{\frac {1}{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\right]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bfc59bbda2a5d28aff70e34cabe94e5626f2cd56)












![{\displaystyle \delta _{s}x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{is}\left(\mathbf {r} \cdot \mathbf {p} \right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc05a043d35a8057d499c9388942a81fb94c7eee)

![{\displaystyle A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \right)\right]-mk\left({\frac {x_{s}}{r}}\right)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \right)\right]_{s}-mk\left({\frac {x_{s}}{r}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85385129547171f032803166f12ce1d75c812f93)












