동형관계

수학에서 집합 X의 동차 관계(내연관이라고도 함)는 X와 자신 사이의 이항 관계, 즉 데카르트 곱 X $X$ 의 부분 집합입니다.^[1]^[2]^[3]이는 일반적으로 "X 위의 관계"^[4] 또는 "X 위의 (이진) 관계"로 표현됩니다.^[5]^[6]동질적인 관계의 예로는 사람들 사이의 관계가 있는 친족 관계가 있습니다.

일반적인 내접 관계 유형에는 순서, 그래프 및 동등성이 포함됩니다.질서 이론과 그래프 이론에 대한 전문적인 연구는 내인 관계에 대한 이해를 발전시켰습니다.그래프 이론에 대한 특정 용어는 설명에 사용되며, 일반적인 (방향이 없는) 그래프는 대칭 관계에 해당하고, 일반적인 내향 관계는 방향이 지정된 그래프에 해당합니다.내향 관계 R은 0과 1의 논리 행렬에 해당하며, 여기서 식 xRy는 그래프에서 x와 y 사이의 간선에 해당하고 R의 제곱 행렬에서는 1에 해당합니다.그래프 용어에서 인접 행렬이라고 합니다.

특정 동질 관계

(임의 원소 $x 1$ , $x$ 를₂ 갖는) 집합 X에 대한 일부 특정한 동질 관계는 다음과 같습니다.

빈 관계
$E$ $= \emptyset$ ;
즉, $xEx$ 는₁₂ 결코 유지되지 않습니다.
보편적 관계
$U$ $=$ X × $X$ ;
즉, $xUx$ 는₁₂ 항상 유지됩니다.
항등식 관계(항등식 함수 참조)
$I$ $= {(x,$ $x) x$ $\in$ $X$ };
즉, $xX$ 는 $x$ = $x$ 인 경우에만 고정됩니다.

예

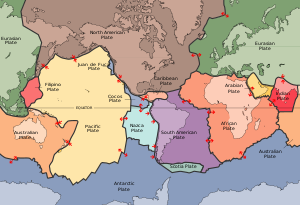
지각의 15개의 큰 지각판들은 서로 균일한 관계로 접촉합니다.관계는 접촉을 나타내는 1과 접촉 없음을 나타내는 0의 논리 행렬로 표현할 수 있습니다.이 예제는 대칭 관계를 나타냅니다.

특성.

집합 $X$ 에 대한 동차 관계 $R$ 이 가질 수 있는 몇 가지 중요한 속성은 다음과 같습니다.

반사적: 모든 $x$ ∈ $X$ , $xRx$ 에 대해.예를 들어, ≥은 반사적 관계이지만 >은(는) 그렇지 않습니다.
무굴절(또는 엄격): $xRx$ 가 아닌 모든 $x$ ∈ $X$ 에 대해.예를 들어 >는 무반향 관계이지만 ≥는 그렇지 않습니다.
코어플렉시블: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $x$ = $y$ .예를 들어, 각 홀수가 자신과 연관된 정수에 대한 관계는 핵심 유연 관계입니다.등식 관계는 반사 관계와 코어 굴곡 관계 모두의 유일한 예이며, 코어 굴곡 관계는 동일성 관계의 부분 집합입니다.
좌측 준반사: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $xRx$ .
우측 준반사: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $yRy$ .
준반사: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $xRx$ 와 $yRy$ .관계는 왼쪽과 오른쪽 모두 준반사인 경우에만 준반사입니다.

이전의 6가지 대안은 완전하지 않습니다. 예를 들어, $y$ = $x$ 로 정의된 이진 관계 $xRy$ 는 ( $0,$ 0 $),$ $(2,$ 4 $)$ 쌍을각각 포함하지만 $(2,$ 2)는 포함하지 않기 때문에 무굴절적이지도 않고 코어플렉시브적이지도 않으며 반사적이지도 않습니다.후자의 두 가지 사실은 또한 (어떤 종류의) 준 반사성을 배제합니다.

대칭적인: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $yRx$ .예를 들어, $x$ 가 y의 혈연이고 $y$ 가 $x$ 의 혈연인 경우에만 x가 $y$ 의 혈연이기 때문에 "is is a blood relative of"는 대칭 관계입니다.
반대칭성: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy$ 와 $yRx$ 라면 $x$ = $y$ .예를 들어, ≥은 반대칭 관계이며 >의 경우에도 마찬가지이지만 모호합니다(정의의 조건은 항상 거짓임).
비대칭: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $xRy이면$ $yRx$ 가 아닙니다.관계가 대칭적이고 비반전적인 경우에만 비대칭적입니다.^[9]예를 들어 >는 비대칭 관계이지만 ≥는 그렇지 않습니다.

$역시$ 이전의 세 가지 대안은 완전하지 않습니다. 자연수에 대한 예로서 x > $2$ 에 의해 정의된 $xRy$ 관계는 비대칭은 말할 것도 없고 대칭도 아닙니다.

트랜지티브: 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $xRy$ 와 $yRz이면$ $xRz$ .전이 관계는 비대칭인 경우에만 비반전적입니다.^[10]예를 들어 "is parent of"는 경과 관계인 반면 "is parent of"는 그렇지 않습니다.
반전이성: 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $xRy$ 와 $yRz$ 라면, $xRz$ 는 절대로 없습니다.
공동 추이성: R의 보어가 추이적인 경우.즉, 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $xRz이면$ , $xRy$ 또는 $yRz$ .이것은 구성 수학에서 의사 차수에 사용됩니다.
준전이성: 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $xRy$ 와 $yRz$ 이지만 $yRx$ 도 $zRy$ 도 아닌 경우, $xRz$ 이지만 $zRx$ 도 아닌 경우.
비교 불가능의 전이성: 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, $만약$ $x$ 와 y가 $R$ 에 대하여 비교할 수 없고 $y$ 와 $z$ 에 대하여 동일한 경우라면, $x$ 와 z $또한$ $R$ 에 대하여 비교할 수 없습니다.이것은 약한 순서로 사용됩니다.

다시 말하지만, 이전의 5가지 대안은 완전하지 않습니다.예를 들어, $xRy$ if ( $y$ = 0 $또는$ $y$ = $x +1$ ) 관계는 이러한 속성 중 어느 것도 만족하지 않습니다.반면에, 빈 관계는 그들 모두를 거의 만족시키지 못합니다.

밀도가 높은: $모든$ x, $y$ 는 $xRy$ 와 같이 $X$ 를 ∈하고, $xRz$ 와 $zRy$ 와 같이 일부 $z$ ∈ $X$ 가 존재합니다.이것은 빽빽한 순서로 사용됩니다.
연결된: 모든 $x,$ $y$ ∈ $X$ 에 대하여, 만약 $x$ ≠ $y이면$ $xRy$ 또는 $yRx$ .이 속성을 "total"이라고 부르기도^{[citation needed]} 하며, 아래에 나와 있는 "left/right-total"의 정의와 구분됩니다.
강하게 연결됨: 모든 $x,$ $y$ ∈ $X$ , $xRy$ 또는 $yRx$ 에 대해.또한 이 속성을 "total"이라고 부르기도^{[citation needed]} 하는데, 이는 아래에 나와 있는 "left/right-total"의 정의와 구별됩니다.
트리코토무스속: 모든 $x,$ $y$ ∈ $X$ 에 대해 $xRy$ , $yRx$ $또는$ x = $y$ 홀드 중 하나만 정확하게 지정합니다.예를 들어 >는 삼차 관계인 반면 자연수에 대한 "분할" 관계는 그렇지 않습니다.^[11]
오른쪽 유클리드 (또는 그냥 유클리드): 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $xRy$ 와 $xRz이면$ $yRz$ .예를 들어, $x$ = $y$ 이고 $x$ = $z이면$ $y$ = $z$ 이기 때문에 =는 유클리드 관계입니다.
좌 유클리드: 모든 $x,$ $y,$ $z$ ∈ $X$ 에 대하여, 만약 $yRx$ 와 $zRx$ 라면 $yRz$ .
근거있는: $X$ 의 비어 있지 않은 모든 부분 집합 $S$ 는 $R$ 에 대한 최소 원소를 포함합니다.근거가 충분하다는 것은 하강 사슬 조건(즉, 무한 사슬이 없음... $xR n ...)$ 을 의미합니다. $RxRxRx$ 가₃₂₁ 존재할 수 있음).종속 선택 공리를 가정하면 두 조건은 동등합니다.^[12]^[13]

또한 일반적으로 이항 관계의 모든 속성은 동질 관계에도 적용될 수 있습니다.

세트같은: 모든 $x$ ∈ $X$ 에 대하여, $yRx$ 가 집합이 되도록 하는 $모든$ 클래스의 클래스. (이것은 적절한 클래스에 대한 관계가 허용되는 경우에만 의미가 있습니다.)
좌고유의: 모든 $x,$ $z$ ∈ $X$ 및 $모든$ ∈ $Y$ 에 대하여, 만약 $xRy$ 및 $zRy이면$ $x$ = $z$ .
무가: 모든 $x$ ∈ $X$ 및 $ally$ 에 $대하여$ , z ∈ $Y$ , 만약 $xRy$ 및 $xRz이면$ $y$ = $z$ .
합계(좌측 합계라고도 함): 모든 $x$ ∈ $X$ 에 대하여 $xRy$ 와 같은 ∈ $Y$ 가 존재합니다.이 속성은 연결된 정의와 다릅니다(일부 저자는 총계라고도 함).^{[citation needed]}
주관적(우합계라고도 함): $모든$ ∈ $Y$ 에 대하여 xRy와 같은 $x$ ∈ $X$ 가 존재합니다.

선주문은 반사적이고 전이적인 관계입니다.선형 전순서(linear preorder) 또는 약한 전순서(weak order)라고도 불리는 총 전순서는 반사적이고 전이적이며 연결된 관계입니다.

부분 순서는 반사적이고 반대칭적이며 전이적인 관계입니다.^{[citation needed]}엄격한 부분 순서(strict partial order)는 ^{[citation needed]}무굴곡적이고 반대칭적이며 전이적인 관계입니다.선형 순서, 단순 순서 또는 사슬이라고도 불리는 총 순서는 반사적이고 반대칭적이며 전이적이고 연결된 관계입니다.^[15]엄격한 선형 순서, 엄격한 단순 순서 또는 엄격한 사슬이라고도 불리는 엄격한 총 순서는 굴절되지 않고 반대칭적이며 전이적이며 연결된 관계입니다.

편등식 관계는 대칭적이고 전이적인 관계입니다.등가 관계는 반사적, 대칭적, 전이적 관계입니다.또한 이러한 특성은 반사성을 의미하기 때문에 대칭, 전이, 총 관계입니다.

동질이진관계의 속성간 함의와 충돌
동질적인 이진 관계의 속성 간의 의미(파란색)와 충돌(빨간색).예를 들어, 모든 비대칭 관계는 무반사("ASym ⇒ Refl")이고, 비어 있지 않은 집합에 대한 어떤 관계도 무반사 및 반사("Irrefl # Refl")일 수 없습니다.빨간색 모서리를 생략하면 Hasse 다이어그램이 생성됩니다.

작전

만약 R이 집합 X에 대한 동차 관계라면, 다음 각각은 X에 대한 동차 관계입니다.

반사⁼ 폐쇄, R: $R$ = ${(x,$ $x) x$ ∈ $X}$ ∪ R $또는$ R을 포함하는 X에 대한 가장 작은 반사 관계로 정의됩니다.이것은 R을 포함하는 모든 반사 관계의 교집합과 동일함을 증명할 수 있습니다.
반사^≠ 감소, R: $R$ = $R$ \ ${(x,$ $x) x$ ∈ $X$ }로 정의되거나 R에 포함된 X에 대한 가장 큰 무반전 관계.
과도⁺ 폐쇄, R: R을 포함하는 X에 대한 가장 작은 전이 관계로 정의됩니다.이것은 R을 포함하는 모든 전이 관계의 교집합과 같다고 볼 수 있습니다.
반사성 전이 폐쇄, R*: $R *$ =( $R$ )로 정의되며 $,$ R을 포함하는 가장 작은 전순서입니다.
반사형^≡ 전이 대칭 폐쇄, R: R을 포함하는 X에 대한 가장 작은 동등성 관계로 정의됩니다.

이항 관계 § 연산에 정의된 모든 연산은 동종 관계에도 적용됩니다.

재산별 동형관계
	반사율	대칭성	전이성	연결성	기호.	예
방향 그래프					→
무방향 그래프		대칭적인
의존	반사적	대칭적인
토너먼트	무굴절	비대칭				서열
선주문	반사적		트랜지티브		≤	선호
총선주문량	반사적		트랜지티브	연결된	≤
부분순서	반사적	반대칭성	트랜지티브		≤	부분 집합
엄밀한부분순서	무굴절	비대칭	트랜지티브		<	엄격 부분 집합
총순서	반사적	반대칭성	트랜지티브	연결된	≤	알파벳순
엄격합계순서	무굴절	비대칭	트랜지티브	연결된	<	엄격한 알파벳 순서
편등식 관계		대칭적인	트랜지티브
동치관계	반사적	대칭적인	트랜지티브		∼, ≡	이퀄리티

열거

집합 X에 대한 ${\mathcal {B}}(X)$ 모든 동차 관계 ${\mathcal {B}}(X)$ ( ${\mathcal {B}}(X)$ ${\displaystyle {\mathcal {B}}(X)$ 의 집합은 그 역관계에 대한 관계의 매핑의 진화로 증강된 부울 대수인 집합 $2$ 입니다^{X × X}. ${\mathcal {B}}(X)$ ( ${\mathcal {B}}(X)$ ${\displaystyle {\mathcal {B}}(X)$ 에 대한 이진 연산으로 관계 구성을 고려하면 ${\mathcal {B}}(X)$ 항등식 요소가 항등식 관계인 모노이드를 형성합니다.^[16]

n-원소 집합에 대한 서로 다른 동형 관계의 수는 $2 n 2$ (OEIS의 수열 A002416)입니다.

서로 다른 유형의 n-요소 이진 관계 수

요소	조금도	트랜지티브	반사적	대칭적인	선주문	부분순서	총선주문량	총순서	동치관계
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
n	2^n²		2ⁿ⁽ⁿ⁻¹⁾	2^n(n+1)/2			∑ⁿkⁿ _k=0!S(n,k)	n!	∑ⁿSⁿ _k=0(n,k)
OEIS	A002416	A006905	A053763	A006125	A000798	A001035	A000670	A000142	A000110

$S (n,$ $k)$ 는 두 번째 종류의 스털링 수를 가리킵니다.

주의:

반사적 관계의 수는 반사적 관계의 수와 같습니다.
엄격한 부분 주문의 수(불굴절 전이 관계)는 부분 주문의 수와 동일합니다.
엄격한 약한 주문의 수는 전체 예약 주문의 수와 같습니다.
총 주문량은 부분 주문량이며, 이 역시 총 예약 주문량입니다.따라서 부분주문도 아니고 전체 예약주문도 아닌 예약주문의 수는 예약주문의 수에서 부분주문의 수를 뺀 수에서 전체 예약주문의 수를 뺀 수를 각각 0, 0, 0, 3, 85.
등가 관계의 수는 파티션의 수이며, 이는 벨 번호입니다.

동차 관계는 쌍(relation, 보)으로 그룹화할 수 있지만, $n$ = $0$ 을 제외하면 관계는 그 자체의 보어입니다.비대칭인 것은 4배(관계, 상보, 역보, 역보)로 그룹화할 수 있습니다.

예

엄격한 주문을 포함한 주문 관계:
- 보다 큼
- 보다 크거나 같음
- 보다 적은
- 작거나 같음
- 나눗셈 (균등)
- 부분 집합
동등성 관계:
- 이퀄리티
- (아핀 공간의 경우)와 평행
- 등심도 또는 "와 사투 중"
- 동형
- 등분극 선분
허용 오차 관계, 반사 및 대칭 관계:
- 종속성 관계, 유한 공차 관계
- 독립성 관계, 어느 정도의 종속성 관계의 보완
친족관계

일반화

일반적으로 이항 관계는 동차일 필요는 없으며, 임의의 집합 X와 Y에 대한 부분 집합 R ⊆ X × Y라고 정의됩니다.
유한 관계는 부분 집합 R ⊆ X × ...× 일부_n 자연수 n과 임의의 집합 X₁, ..., X에_n 대해서는 n-ary 관계라고도 합니다.

참고문헌

^ Michael Winter (2007). Goguen Categories: A Categorical Approach to L-fuzzy Relations. Springer. pp. x–xi. ISBN 978-1-4020-6164-6.
^ M. E. Müller (2012). Relational Knowledge Discovery. Cambridge University Press. p. 22. ISBN 978-0-521-19021-3.
^ Peter J. Pahl; Rudolf Damrath (2001). Mathematical Foundations of Computational Engineering: A Handbook. Springer Science & Business Media. p. 496. ISBN 978-3-540-67995-0.
^ Mordeson, John N.; Nair, Premchand S. (8 November 2012). Fuzzy Mathematics: An Introduction for Engineers and Scientists. Physica. p. 2. ISBN 978-3-7908-1808-6.
^ Tanaev, V.; Gordon, W.; Shafransky, Yakov M. (6 December 2012). Scheduling Theory. Single-Stage Systems. Springer Science & Business Media. p. 41. ISBN 978-94-011-1190-4.
^ Meyer, Bertrand (29 June 2009). Touch of Class: Learning to Program Well with Objects and Contracts. Springer Science & Business Media. p. 509. ISBN 978-3-540-92145-5.
^ 폰세카 데 올리베이라, J.N. & Pereira Cunha Rodrigues, C.D.J. (2004)관계 전환: Maybe Functions에서 Hash Tables로.프로그램 구성 수학(Mathematics of Program Construction)에서 (p. 337).
^ Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, p. 160, ISBN 0-534-39900-2
^ Nievergelt, Yves (2002), Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography, Springer-Verlag, p. 158.
^ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). Transitive Closures of Binary Relations I (PDF). Prague: School of Mathematics – Physics Charles University. p. 1. Archived from the original (PDF) on 2013-11-02. 보조 인자 1.1(iv).이 소스는 비대칭 관계를 "엄격하게 반대칭"이라고 말합니다.
^ 5가 3을 나누지도 않고, 3이 5를 나누지도 않고, 3=5를 나누지도 않기 때문입니다.
^ "Condition for Well-Foundedness". ProofWiki. Archived from the original on 20 February 2019. Retrieved 20 February 2019.
^ Fraisse, R. (15 December 2000). Theory of Relations, Volume 145 - 1st Edition (1st ed.). Elsevier. p. 46. ISBN 9780444505422. Retrieved 20 February 2019.
^ Gunther Schmidt & Thomas Strohlein (2012)[1987] 관계와 그래프, p. 54, Google Books
^ Joseph G. Rosenstein, 선형 순서, Academy Press, 1982, ISBN 0-12-597680-1, 페이지 4
^ Schmidt, Gunther; Ströhlein, Thomas (1993). "Homogeneous Relations". Relations and Graphs: Discrete Mathematics for Computer Scientists. Berlin, Heidelberg: Springer. p. 14. doi:10.1007/978-3-642-77968-8_2. ISBN 978-3-642-77968-8.

[Winter2007-1] Michael Winter (2007). Goguen Categories: A Categorical Approach to L-fuzzy Relations. Springer. pp. x–xi. ISBN 978-1-4020-6164-6.

[Müller2012-2] M. E. Müller (2012). Relational Knowledge Discovery. Cambridge University Press. p. 22. ISBN 978-0-521-19021-3.

[PahlDamrath2001-p496-3] Peter J. Pahl; Rudolf Damrath (2001). Mathematical Foundations of Computational Engineering: A Handbook. Springer Science & Business Media. p. 496. ISBN 978-3-540-67995-0.

[4] Mordeson, John N.; Nair, Premchand S. (8 November 2012). Fuzzy Mathematics: An Introduction for Engineers and Scientists. Physica. p. 2. ISBN 978-3-7908-1808-6.

[5] Tanaev, V.; Gordon, W.; Shafransky, Yakov M. (6 December 2012). Scheduling Theory. Single-Stage Systems. Springer Science & Business Media. p. 41. ISBN 978-94-011-1190-4.

[6] Meyer, Bertrand (29 June 2009). Touch of Class: Learning to Program Well with Objects and Contracts. Springer Science & Business Media. p. 509. ISBN 978-3-540-92145-5.

[7] 폰세카 데 올리베이라, J.N. & Pereira Cunha Rodrigues, C.D.J. (2004)관계 전환: Maybe Functions에서 Hash Tables로.프로그램 구성 수학(Mathematics of Program Construction)에서 (p. 337).

[8] Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, p. 160, ISBN 0-534-39900-2

[9] Nievergelt, Yves (2002), Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography, Springer-Verlag, p. 158.

[10] Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). Transitive Closures of Binary Relations I (PDF). Prague: School of Mathematics – Physics Charles University. p. 1. Archived from the original (PDF) on 2013-11-02. 보조 인자 1.1(iv).이 소스는 비대칭 관계를 "엄격하게 반대칭"이라고 말합니다.

[11] 5가 3을 나누지도 않고, 3이 5를 나누지도 않고, 3=5를 나누지도 않기 때문입니다.

[12] "Condition for Well-Foundedness". ProofWiki. Archived from the original on 20 February 2019. Retrieved 20 February 2019.

[13] Fraisse, R. (15 December 2000). Theory of Relations, Volume 145 - 1st Edition (1st ed.). Elsevier. p. 46. ISBN 9780444505422. Retrieved 20 February 2019.

[14] Gunther Schmidt & Thomas Strohlein (2012)[1987] 관계와 그래프, p. 54, Google Books

[15] Joseph G. Rosenstein, 선형 순서, Academy Press, 1982, ISBN 0-12-597680-1, 페이지 4

[16] Schmidt, Gunther; Ströhlein, Thomas (1993). "Homogeneous Relations". Relations and Graphs: Discrete Mathematics for Computer Scientists. Berlin, Heidelberg: Springer. p. 14. doi:10.1007/978-3-642-77968-8_2. ISBN 978-3-642-77968-8.

[1]

[2]

[3]

[4]

[5]

[6]

[9]

[10]

[11]

[12]

[13]

[15]

[16]

Search

동형관계

네임스페이스

더

목차

특정 동질 관계

예

특성.

작전

열거

예

일반화

참고문헌