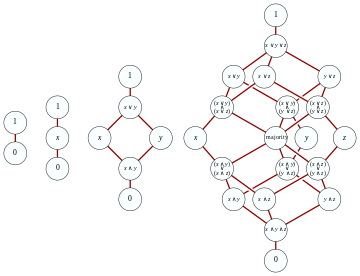
분배 격자

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "분산 격자" – 뉴스 · 신문 · 도서 · 학자 · JSTOR(2011년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

수학에서, 분배 격자는 결합하고 만나는 운영이 서로에 대해 분배되는 격자다. 그러한 구조물의 프로토타입 예는 격자 연산을 세트 유니언과 교차점에 의해 제공할 수 있는 집합이다. 실제로, 이러한 집합의 격자는 풍경을 완전히 묘사한다: 모든 분배 격자는 그러한 집합의 격자로 주어지는 (이형성까지) 이형성에 이른다.

정의

임의 격자의 경우와 마찬가지로, 분배 격자 L을 순서 이론의 구조 또는 보편 대수 구조로 고려할 수 있다. 두 견해와 상호간의 서신은 모두 선반에 관한 기사에서 논의된다. 현 상황에서는 대수적 설명이 더 편리한 것 같다.

격자(L, lartice, l, laughter, laughter)는 L의 모든 x, y, z에 대해 다음과 같은 추가 식별이 유지될 경우 분배된다.

x ∧ (y ∨ z) = (x ∧ y) ∨ (x ∧ z)

래치를 부분적으로 정렬된 집합으로 보면, 이는 만족 연산이 비어 있지 않은 유한 조인트를 보존한다는 것을 의미한다. 위의 조건이 그 이중과 같다는 것은 격자 이론의 기본적인 사실이다.^[1]

x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z) L의 모든 x, y, z에 대한 ∧ (x ∨ z)^[2]

p latq=p를 의미하기 위해 pqq를 평상시와 같이 정의하는 모든 격자에서는 불평등 x y (y ) z) x (x z z) x (x ) z)는 그 이중 불평등 x ) (y z z) ∧ (x ∨ z) ∧ (x ∨ z)을 지탱한다. 반대편 불평등 중 하나가 유지된다면 격자는 분배적인 것이다. 순서 이론의 다른 분배 조건과 이 조건의 관계에 대한 자세한 정보는 분배성에 관한 기사(질서 이론)에서 찾을 수 있다.

형태론

분배 격자의 형태론은 격자에 관한 기사, 즉 두 격자 연산과 양립할 수 있는 함수에서 제시된 격자 동형성에 불과하다. 이러한 격자 형태론은 격자 구조를 보존하기 때문에, 결과적으로 분배성(따라서 분배 격자의 형태론)도 보존할 것이다.

예

분배 격자는 어디에나 있지만 특정한 구조도 있다. 이미 언급한 바와 같이, 분배 격자의 주요 예는 집합의 격자이며, 여기서 결합과 만남은 통상적인 집합-이론적 연산에 의해 주어진다. 그 밖의 예는 다음과 같다.

• 연결과 분리를 지원하는 대부분의 로직의 린덴바움 대수학(Lindenbaum 대수학)은 분배 격자, 즉 "그리고"는 "또는" 위에 분포하고 그 반대도 마찬가지다.
• 모든 부울대수는 분배 격자야.
• 모든 헤이팅 대수학은 분배 격자야. 특히 여기에는 모든 국소 및 위상학적 공간의 모든 열린 집합 격자가 포함된다. 또한 헤잉 알헤브라는 직관적 논리의 린덴바움 알헤브라로 볼 수 있으며, 이것이 첫 번째 사례의 특별한 경우를 만든다는 점에 주목한다.
• 완전히 주문된 모든 세트는 최대 결합과 최소 결합을 가진 분배 격자다.
• 자연수는 가장 큰 공통점을 충족시키고 가장 작은 공통 배수를 결합으로 취함으로써 분배 격자를 형성한다. 또한 이 격자에는 최소 요소, 즉 1이 있어 결합을 위한 ID 요소 역할을 한다.
• 양의 정수 n이 주어지면, n의 모든 양의 구분자 집합은 분배 격자를 형성하며, 다시 최대 공통 구분자 집합은 만나는 것이고 최소 공통 구분자는 결합하는 것이다. n이 제곱이 없는 경우에만 부울 대수다.
• 격자 순서의 벡터 공간은 분배 격자 공간이다.
• 정수 칸막이를 나타내는 영 도표의 포함 순서에 의해 영의 격자는 분배 격자다.
• 분산형 폴리토프(좌표상 최소 및 좌표상 최대 연산에 따라 닫히는 볼록형 폴리토프)의 지점이며, 이 두 연산을 격자의 결합 및 만족 연산으로 한다.^[3]

격자 이론의 발달 초기에는 찰스 S. Peirce는 모든 격자는 분배적, 즉 분배성은 나머지 격자 공리에서 나온다고 믿었다.^[4][5] 그러나 독립 증명서는 슈뢰더, 보이트, ^(de)뤼트로트, 코르셀트, ^[6]데데킨드에 의해 제시되었다.^[4]

특성 특성

상기의 정의에 상당하는 다양한 제형이 존재한다. 예를 들어 L은 L의 모든 원소 x, y, z에 대해 다음이 유지되는 경우에만 분배된다.

(x${\displaystyle \wedge }$y)${\displaystyle \vee }$(y${\displaystyle \wedge }$z)${\displaystyle \vee }$(z${\displaystyle \wedge }$x) = (x${\displaystyle \vee }$y)${\displaystyle \wedge }$(y${\displaystyle \vee }$z)${\displaystyle \wedge }$(z${\displaystyle \vee }$x).

마찬가지로 L은 만약의 경우에 한해서만 분배된다.

x ${\displaystyle }$ ${\displaystyle \wedge}$z = y ${\displaystyle }$ ${\displaystyle \wedge}$ $z$ 및 x ${\displaystyle }$ ${\displaystyle \ve }$ $z$ = y ${\displaystyle }$ ${\displaystyle \ve}$ $z$는 항상 x=y를 의미한다.

• 두 개의 표준형 비분배 래티스의 Hasse 다이어그램
• 

  다이아몬드 격자 M은₃ 비분배적이다: x ∧ (y ∨ z) = x ∧ 1 = x ≠ 0 = 0 ∨ 0 = (x ∧ y) ∨ (x ∧ z)

• 

  펜타곤 격자 N은₅ 비분배적이다: x ∧ (y ∨ z) = x ∧ 1 = x ≠ z = 0 ∨ z = (x ∧ y) ∨ (x ∧ z)

가장 단순한 비분배 격자는 "다이아몬드 격자"인₃ M과 "펜타곤 격자"인₅ N이다. 격자는 그 하위 격자가 M 또는₃ N에₅ 이형성이 없는 경우에만 분배된다. 하위 격자는 원래 격자의 충족 및 결합 운영에 따라 닫히는 하위 집합이다. 이는 원래 순서에 따라 격자(조인 및 미팅 작업이 다를 수 있음)인 부분 집합과 같지 않다는 점에 유의하십시오. 추가 특성화는 다음 절의 표현 이론에서 도출된다.

동일한 사실을 진술하는 다른 방법은 모든 분배 격자는 2개 요소 사슬의 복사본의 하위 직접 제품이거나, 또는 분배 격자 등급의 유일한 하위 분해할 수 없는 구성원은 2개 요소 사슬이라는 것이다. 각 부울 격자에는 이 속성도 있다.^[7]

마지막으로 분배성은 몇 가지 다른 즐거운 성질을 수반한다. 예를 들어, 분배 격자의 요소는 일반적으로 더 약한 특성이지만, 충족 불가한 경우에만 충족 프라임이다. 이중성에 의해, 가입 프라임과 가입 불가 요소도 마찬가지다.^[8] 격자가 분포적인 경우 격자의 피복 관계는 중위수 그래프를 형성한다.^[9]

게다가, 모든 분배 격자 또한 모듈형이다.

표현 이론

도입부는 이미 분배 격자에 대한 가장 중요한 특성화를 시사했다. 격자는 집합의 격자에 이형인 경우에만 분배된다(세트 유니언과 교차점에 따라 폐쇄됨). (후자의 구조를 이 맥락에서 집합의 고리라고 부르기도 한다.) 그 집합적 결합과 교차점은 실제로 위의 의미에서 분배적인 것이다. 다른 방향은 아래에 기술된 표현 이론이 필요하다는 점에서 덜 사소한 것이다. 이러한 특성화의 중요한 통찰력은 모든 분배 격자를 보유하는 정체성(등분)이 상기의 의미에서 모든 집합 격자를 보유하는 정체성(등분)이라는 것이다.

비르코프의 분배 격자에 대한 대표 정리에서는 모든 유한 분배 격자는 그 결합-우량(동등하게: 결합-불가역) 요소의 하위 집합의 격자와 이형성이 있다고 명시하고 있다. 이것은 모든 유한양행의 등급과 모든 유한양행 래트 등급 사이의 편향(이형성에 이르는)을 설정한다. 이러한 편향은 유한분포 래티스의 동형식과 유한양점의 모노톤 함수 사이의 범주의 이중성으로 확장될 수 있다. 그러나 이 결과를 무한대 격자로 일반화하려면 추가적인 구조를 추가해야 한다.

또 하나의 초기 표현 정리는 현재 분배 격자를 위한 스톤의 표현 정리(이름은 처음 그것을 증명했던 마샬 하비 스톤을 기린다)로 알려져 있다. 그것은 특정 위상학적 공간의 콤팩트한 열린 집합의 격자로 분배 격자를 특징짓는다. 이 결과는 스톤이 부울 알헤브라에 대해 유명했던 표현 정리의 일반화와 스톤 이중성의 일반적 설정의 전문화로 볼 수 있다.

힐러리 프리스틀리가 분배 선반들에 대한 그녀의 대표 정리에서 더 중요한 대표성이 확립되었다. 이 공식에서, 분배 격자는 점들에 추가적인 부분적인 순서가 있는 위상학적 공간을 건설하는데 사용되며, 순서가 완전히 분리된 (또는 프리스틀리 공간)을 산출한다. 원래 격자는 이 공간의 클오픈 하부 세트 모음으로 복구된다.

스톤과 프리스틀리의 이론의 결과로, 어떤 분배 격자는 세트 격자와 정말로 이형성이 있다는 것을 쉽게 알 수 있다. 그러나 두 진술의 증명에는 선택의 공리의 약한 형태인 부울 프라임 이상 정리가 필요하다.

자유분배 선반

발전기 G에 대한 자유 분배 격자는 일반 자유 격자보다 훨씬 쉽게 건설될 수 있다. 첫 번째 관찰은 분배성의 법칙을 이용하여 발전기 집합에서$$ 이진 연산 operations${\displaystyle \lor$} 및$$ $\wedge {\displaystyle }$ ${\displaystyle \land }$에 의해 형성된 모든 용어를 다음과 같은 동등한 정상 형태로 변환할 수 있다는 것이다.

${\displaystyle M_{1}\lor M_{2}\lor \cdots \lor M_{n}}$

여기서 $M{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 G의 요소들의 유한한 만남이다$$. 더욱이 만남과 결합은 모두 연관성, 교감성, idempotent이기 때문에 중복과 순서를 무시할 수 있으며, 위의 만남과 같은 모임의 조인을 집합으로 나타낼 수 있다.

${\displaystyle \{{N_{1},N_{2},\ldots,N_{n}\}}$

여기서 ${\displaystyle {Ni}_{}}$ ${\$는 G의 유한 부분 집합이다$$. 그러나 그러한 두 용어가 분배 격자의 동일한 요소를 나타내는 것은 여전히 가능하다. $이$는 N ${\displaystyle j_{}}$ ${\$이(가) $N{\displaystyle {}_{}}$ ${\displaystyle k_{}}$. ${\displaystyle N_{k}$의 하위 집합인$$ 인덱스 j와 k가 있을 때 발생한다.$}}$ 이 경우$$ $N{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$의 만남이 $N{\displaystyle {}_{}}$ ${\displaystyle j_{}}$, ${\displaystyle N_{j}$의 만남보다 아래에 있으므로$$$$ 전체 용어의 해석을 변경하지 않고$$ 중복 집합 $N{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$을 안전하게 제거할 수 있다. 따라서 G의 유한 부분 집합은 그 모든 요소 ${\$이 상호$$ 비교 불가할 때마다, 즉 유한 집합의 반차를 형성할 때, 무한 반복이라고 불릴 것이다.

이제 발전기 G에 대한 자유 분배 격자는 G의 모든 유한 부분 집합의 유한 초과 집합 집합에 정의된다. 두 개의 유한 중복 집합의 결합은 모든 중복 집합을 제거하여 조합으로부터 얻는다. 마찬가지로 두 세트 S와 T의 만남은 $\{{\displaystyle N}$ ${\displaystyle \cup }$ ${\displaystyle M}$ ${\displaystyle \mid }$ ${\displaystyle N\in }$ S, ${\displaystyle M}$ ${\displaystyle \in }$ T ${\displaystyle \}}$의 중복된 버전이다${\displaystyle .}$ ${\displaystyle \{N\cup$M\$mid$N\$in$ S$,M\in$ T$\}}$이 구조가 필요한 보편적 속성의 분배 격자임을 확인하는 것은 일상적인$$ 일이다.

발전기가 n개인 자유분산 격자의 요소 수는 디데킨드 숫자로 주어진다. 이 숫자들은 빠르게 증가하며, 오직 n 8 8로 알려져 있다.

2, 3, 6, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788(OEIS의 후속 A000372).

위의 숫자는 격자 연산이 결합되고 빈 집합을 포함한 유한 요소 집합의 유한한 집합이 충족되는 자유 분배 격자 내 요소 수를 계산한다. 빈 조인과 빈 조인이 허용되지 않는 경우, 결과적인 자유 분배 래티들은 두 개의 요소를 더 적게 가지고 있다; 요소들의 수는 순서를 형성한다.

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 5613043722868575907786(OEIS의 후속 A007153).

참고 항목

• 완전 분배 격자 — 무한 결합을 통해 무한 결합을 분배하는 격자가 만나는 격자
• 분배 격자의 이중성 이론
• 스펙트럼 공간

참조

추가 읽기

• Burris, Stanley N.; Sankappanavar, H.P. (1981). A Course in Universal Algebra. Springer-Verlag. ISBN 3-540-90578-2.
• OEIS 시퀀스 A006982(n 요소가 있는 레이블이 없는 분배 래티 수)