양자 우물

양자 웰.양자 효과를 발생시키는 나노미터 단위의 헤테로 구조 체계.길이가 L인 음영 부분은 일정한(이산) 원자가 ^[1]밴드가 있는 영역을 나타냅니다.

양자 우물은 분리된 에너지 값만 있는 전위 우물이다.

양자 우물 시연에 사용되는 고전적인 모델은 처음에는 3차원으로 자유롭게 움직일 수 있었던 입자를 평면 영역을 차지하도록 강요함으로써 2차원으로 제한하는 것이다.양자 구속의 효과는 양자 우물 두께가 캐리어의 드 브로글리 파장과 비슷해지면서 "에너지 서브밴드"라고 불리는 에너지 수준으로 이어질 때 발생한다. 즉, 캐리어는 별개의 에너지 값만 가질 수 있다.

다양한 전자 양자 우물 장치들이 양자 우물 시스템의 이론에 기초하여 개발되어 왔다.이러한 디바이스는 레이저, 광검출기, 변조기, 스위치 등에서 사용되고 있습니다.기존 장치에 비해 양자 우물 장치는 훨씬 더 빠르고 경제적으로 작동하며 기술 및 통신 산업에 매우 중요한 지점입니다.이러한 양자 우물 장치는 현재 많은 전자 장치의 ^[2]전통적인 전기 부품을 전부는 아니더라도 대체하고 있습니다.

양자 우물의 개념은 1963년 Herbert Kroemer와 Zhores Alferov와 R.F. Kazarinov에 ^[3]^[4]의해 독립적으로 제안되었다.

역사

반도체 양자 유정은 1970년 에사키와 쯔에 의해 개발되었으며, 그는 합성 초격자를 ^[5]발명하기도 했다.그들은 서로 다른 밴드갭을 가진 얇은 반도체 층을 번갈아 가며 구성된 헤테로 구조가 흥미롭고 유용한 ^[6]특성을 보여야 한다고 제안했다.그 이후로 많은 노력과 연구가 양자 우물 시스템의 물리학 연구와 양자 우물 장치 개발에 투입되었다.

양자 우물 소자의 발달은 결정 성장 기술의 발달에 크게 기인한다.양자 우물 소자는 결함이 거의 없고 순도가 높은 구조를 필요로 하기 때문이다.따라서 이러한 헤테로 구조의 성장을 잘 제어함으로써 매우 미세 조정된 ^[5]특성을 가진 반도체 소자를 개발할 수 있습니다.

양자 유정과 반도체 물리학은 물리학 연구에서 뜨거운 주제가 되어 왔다.여러 ^[7]개의 반도체로 구성된 구조를 이용한 반도체 소자 개발로 2000년 조르스 알페로프와 헤르베르트 크로이머가 노벨상을 받았다.

양자 우물 소자를 둘러싼 이론은 발광 다이오드, 예를 들어 트랜지스터와 같은 많은 현대 부품들의 생산과 효율에 있어 상당한 발전을 가져왔다.오늘날, 그러한 장치들은 현대의 휴대전화, 컴퓨터, 그리고 많은 다른 컴퓨터 장치들에 어디에나 존재한다.

제조

양자우물은 비화 갈륨과 같은 물질이 알루미늄 비소와 같이 넓은 밴드갭을 가진 물질의 두 층 사이에 끼임으로써 반도체에서 형성된다. (다른 예: 질화 갈륨의 두 층 사이에 끼임)이러한 구조는 분자 빔 에피택시 또는 단분자층까지 층 두께를 제어하는 화학적 증기 증착에 의해 성장할 수 있습니다.

박막은 양자 우물 상태, 특히 금속 및 반도체 표면에서 성장한 얇은 금속 오버레이도 지원할 수 있습니다.진공-금속 인터페이스는 반도체 기판과의 절대적인 간격 또는 금속 기판과의 투영된 밴드 간격에 의해 전자(또는 구멍)를 한쪽에 구속합니다.

QW 재료 시스템을 성장시키는 방법에는 격자 매칭, 변형 균형 및 ^[8]변형률의 3가지가 있습니다.

격자 매칭 시스템:격자 매칭 시스템에서 웰과 장벽은 기초 기판 재료와 ^[8]유사한 격자 정수를 가진다.이 방법을 사용하면 밴드갭 차이가 최소 전위일 뿐 아니라 흡수 스펙트럼의 이동도 최소화된다.
변형률 균형 시스템:스트레인밸런스 방식에서는 한쪽 층의 격자상수 증가가 기판재료에 비해 다음 층의 격자상수 감소로 보상되도록 웰 및 장벽을 성장시킨다.층의 두께와 구성은 밴드갭 요건과 반송파 전송 제한에 영향을 미칩니다.이 접근방식은 설계의 유연성을 최대한 높여 응력 ^[8]완화를 최소화하면서 많은 수의 정기적인 QW를 제공합니다.
변형된 시스템:변형 시스템은 격자 상수가 유사하지 않은 유정과 장벽으로 성장한다.변형 시스템은 구조 전체를 압축합니다.그 결과, 이 구조는 소수의 양자 ^[8]우물만 수용할 수 있습니다.

반도체 AlGaAs(대밴드갭)와 GaAs(대밴드갭)로 이루어진 양자 우물 구성으로 이루어진 헤테로 구조.길이 d의 중심 GaAs 영역에서는 전도 대역 에너지가 낮고, 원자가 대역 에너지가 높다.따라서 전자와 구멍 모두 GaAs 영역에 갇힐 수 있습니다.

설명 및 개요

가장 간단한 양자 우물 시스템 중 하나는 다른 밴드갭을 가진 다른 두 층 사이에 한 종류의 반도체 재료를 얇은 층으로 삽입함으로써 구축될 수 있다.예를 들어 GaAs의 얇은 층을 둘러싼 큰 밴드갭이 있는 2개의 레이어 AlGaA를 보다 작은 밴드갭으로 생각해 봅시다.재료의 변화가 z 방향을 따라 일어나고 따라서 전위 유정이 z 방향을 따른다고 가정합니다(x-y 평면에 구속되지 않음).함유물질의 밴드갭이 주변 AlGaAs보다 낮기 때문에 GaAs 영역에 양자 우물(Potential Well)이 생성된다.구조 전체에 걸친 대역 에너지의 변화는 캐리어가 느낄 수 있는 잠재력의 변화로 볼 수 있으며, 따라서 낮은 에너지 캐리어가 이러한 ^[7]웰에 갇힐 수 있습니다.

AlGaAs 사이에 있는 GaAs의 양자 우물 내 밴드 구조도.전기전도대역의 전자 또는 원자가대역의 구멍은 전기구조물에 형성된 전위우물에 갇힐 수 있다.웰에서 사용 가능한 상태가 그림에 스케치되어 있습니다.이것들은 「상자내의 입자」상태입니다.

양자 우물 내에는 캐리어가 가질 수 있는 이산 에너지 고유 상태가 있습니다.예를 들어, 전도 대역의 전자는 이 구조의 AlGaAs 영역에서보다 우물 내에서 더 낮은 에너지를 가질 수 있습니다.이것에 의해 에너지가 낮은 전도대역의 전자를 양자 우물 내에 포착할 수 있다.마찬가지로, 원자가 밴드의 구멍도 원자가 밴드에 생성된 전위 웰의 상단에 끼일 수 있습니다.밀폐 캐리어가 될 수 있는 상태는 상자 안의 입자 상태입니다.^[5]

물리

양자 우물 및 양자 우물 소자는 오늘날에도 광범위하게 연구되고 연구되고 있는 고체 물리학의 하위 분야입니다.이러한 시스템을 설명하기 위해 사용되는 이론은 양자 물리학, 통계 물리학, 그리고 전기 역학 분야에서 중요한 결과를 사용한다.

무한 우물 모형

양자 우물 시스템의 가장 단순한 모델은 무한 우물 모델이다.이 모델에서는 잠재적 유정의 벽/장벽이 무한하다고 가정한다.양자 우물에서 생성되는 전위 유정은 일반적으로 수백 밀리 전자볼트 정도로 무한히 높은 전위보다 훨씬 작기 때문에 이 근사치는 다소 비현실적이다.그러나 첫 번째 근사치로서 무한 우물 모델은 양자 ^[5]우물 뒤에 있는 물리학에 대한 통찰력을 제공하는 단순하고 유용한 모델 역할을 합니다.

우물 내 캐리어가 z 방향으로 제한되지만 x-y 평면에서 자유롭게 이동할 수 있도록 z 방향으로 방향을 잘 잡은 무한 양자를 고려합니다.z $z=0$ { $displaystyle$ z $=0}$ 에서 $z=0$ z $z=d$ { $displaystyle$ z $=d$ 까지 실행할 양자 우물을 선택합니다. 반송파가 우물 내에서 잠재력을 경험하지 못하고 장벽 영역의 잠재력이 무한히 높다고 가정합니다.

무한 우물 모델에서 반송파에 대한 슈뢰딩거 방정식은 다음과 같습니다.

- {\frac ^{2}} {2m{_{w}^{*}} {\frac {\frac ^{2}\psi (z)} {\frac z^{2}} = E\psi (z)

여기서 $\hbar$ { $displaystyle \hbar}$ 는 $\hbar$ 플랑크의 상수를 $2\pi$ { $displaystyle$ 2 $\pi}($ 으 $2\pi$ )로 $2\pi$ $m_{w}^{*}$ 이고 $m_{w}^{*}$ w ${\$ { $display m_{w}^*}$ 는 $m_{w}^{*}$ 웰 영역 내 캐리어의 유효 질량이다.반송파의 유효 질량은 전자가 양자 환경에서 느끼는 질량으로, 유효 질량의 값은 밴드의 곡률에 따라 크게 달라지기 때문에 일반적으로 서로 다른 반도체 간에 차이가 있습니다. $m_{w}^{*}$ w ${\$ { $displaystyle m_{w}^{*}}$ 는 $m_{w}^{*}$ $m_{w}^{*}$ 대역의 웰 또는 원자가 대역의 웰에 있는 홀의 유효 전자 질량이 될 수 있습니다.

솔루션 및 에너지 수준

무한 우물 양자 우물 모델의 처음 두 에너지 상태.이 모델의 벽은 무한히 높은 것으로 가정합니다.용액 파동 함수는 정현파이며 우물 경계에서 0으로 이동합니다.

용액의 파동 함수는 무한히 높은 잠재력 때문에 유정의 장벽 영역에는 존재할 수 없습니다.따라서 다음과 같은 경계 조건을 부과함으로써 허용되는 파동 함수를 얻을 수 있다.

\displaystyle \psi (0)=\psi (d)=0.}

솔루션 웨이브 함수는 다음과 같은 형태를 취합니다.

\displaystyle \psi _{n}(z)=snrt {frac {2}{d}}\sin(k_{n}z)\qquad k_{n}=snrc {n\pi}{d}}.}

$첨자$ n $n>0$ $displaystyle$ n $)$ 은 정수 양자수를 $나타내고$ $(\$ $n>0$ 은 $k_{n}$ 각 상태와 관련된 파동 벡터입니다.관련 이산 에너지는 다음과 같이 주어진다.

{\displaystyle E_{n}=frac {hbar ^{2}k_{n}^{*}}=frac {hbar ^{2}{2m_{w}^*}}\frac {n\pi }{d}\right}{2}.

단순한 무한 우물 모델은 양자 우물 시스템의 물리학과 양자 구속의 효과를 분석하기 위한 좋은 출발점을 제공합니다.모형은 우물 안의 에너지가 우물 길이의 제곱에 반비례한다고 올바르게 예측합니다.즉, 반도체 층의 폭, 즉 우물 길이에 대한 정밀 제어를 통해 우물 내 캐리어가 허용하는 에너지 수준을 정밀하게 제어할 수 있습니다.이것은 밴드갭 엔지니어링에 매우 유용한 특성입니다.게다가 이 모델은 에너지 레벨이 유효 질량의 역수에 비례한다는 것을 보여준다.따라서 무거운 구멍과 가벼운 구멍은 우물 안에 갇혔을 때 에너지 상태가 달라집니다.무거운 구멍과 가벼운 구멍은 곡률이 다른 원자가 밴드의 최대값이 일치할 때 발생하며, 결과적으로 두 개의 다른 유효 ^[5]질량이 발생합니다.

무한 우물 모델의 단점은 실제 양자 우물 벽이 유한하기 때문에 존재하는 것보다 더 많은 에너지 상태를 예측한다는 것입니다.이 모델은 또한 실제로는 파동 함수가 우물 경계에서 0으로 가는 것이 아니라 (양자 터널링으로 인해) 벽으로 '블링'되어 0으로 기하급수적으로 붕괴한다는 사실을 무시한다.이 특성은 슈퍼래티스와 다른 새로운 양자 우물 장치의 설계와 생산을 허용하며 유한 우물 모델에 의해 더 잘 설명된다.

유한 우물 모형

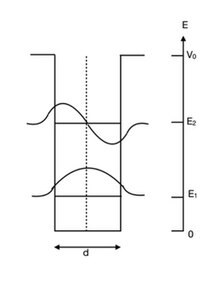
유한 웰 모델은 양자 웰의 보다 현실적인 모델을 제공합니다.여기서 헤테로 구조의 웰 벽은 다른 반도체의 전도 대역 에너지 차이인 유한 $V_{0}$ V $({$ 을 사용하여 모델링됩니다.벽이 유한하고 전자가 장벽 영역으로 터널링할 수 있기 때문입니다.따라서 허용된 파동 기능이 장벽에 ^[6]침투합니다.

유정 내 캐리어가 z 방향으로 제한되지만 x-y 평면에서 자유롭게 이동할 수 있도록 z 방향으로 방향을 잘 잡은 유한한 양자를 고려해보자.z $z=0$ $z=0$ { $displaystyle$ z $=$ $0$ } ~ $z=d$ = d { $d$ 까지의 $z=d$ 유정을 선택합니다. 따라서 캐리어는 장벽 영역에서 V $V_{0}$ { $displaystyle V_{0}$ 의 $V_{0}$ $V_{0}$ 및 잠재력 내에 잠재력이 없다고 가정합니다.

우물 내 반송파에 대한 슈뢰딩거 방정식은 무한 우물 모델과 비교할 때 변경되지 않는다. 단, 벽의 경계 조건은 이제 파동 함수와 그 기울기가 경계에서 연속적일 것을 요구한다.

장벽 영역 내에서, 통신사에 대한 Schrodinger의 방정식은 다음과 같습니다.

- {\frac ^{2}}{2m{_{b}^{*}}{\frac {\frac ^{2}\psi(z)}{\frac z^{2}}+V_{0}\psi(z)=E\psi(z)

$m_{b}^{*}$ 서 m b $∗$ {\ $displaystyle m_{$ b}^{*}}는 $m_{b}^{*}$ 장벽 영역에 있는 캐리어의 유효 질량이며,^[5] 일반적으로 우물 내 유효 질량과 다릅니다.

솔루션 및 에너지 수준

유한 웰 모델의 캐리어를 위한 양자화된 에너지 상태(

E<V_{0}

<

E<V_{0}

0 \

displaystyle

E <

V

_ {

0

} )의 스케치.파동 함수는 정현파형이지만 장벽 영역에서 기하급수적으로 감소합니다.이러한 상태의 에너지는 무한 우물 모델의 에너지보다 작습니다.

관련 경계 조건 및 파동 함수가 우물 가장자리에서 연속되어야 한다는 조건을 사용하여 다음과 같은 초월 방정식을 만족하는 파동 $벡터$ k(\ $displaystyle$ k $)$ 에 $k$ 대한 해법을 구한다.

{{displaystyle\tan\frac {k_{n}d}{2}}\right}=blac {m_{w}{*}\kappa}{m_{b}{k_{n}}}\flac {text{(이븐)}}}}\flac {m_w}}

그리고.

{\displaystyle \tan \frac {k_{n}d}{2}\right}=-{\frac {m_{b}^{*}k_{n}{m_{w}^*}\kappa}}}}}\frac {\text{(홀수)}}},

여기서 $\kappa$ { $displaystyle \kappa}$ 는 $\kappa$ 장벽 영역의 지수 붕괴 상수이며, 장벽 영역의 파동 함수가 0으로 얼마나 빨리 감소하는지를 나타내는 척도입니다.파동 벡터와 양자 번호( $\displaystyle$ n $n$ 에 따라 달라지는 우물 내부의 양자화된 에너지 고유 상태는 다음과 같이 제공됩니다.

({displaystyle E_{n}=blac {hbar ^{2}k_{n}^2}}{2m_{w}^{*}}).}

지수감쇠상수 $\kappa$ \ $kappa)$ 는 $\kappa$ 다음과 같이 구한다.

\kappa = parc frac {2m_{b}^{*}(V_{0}-E_{n})}:{\hbar }

이 값은 결합 $E_{n}$ $E_{n}$ 의 $E_{n}$ 고유 상태(\ $V_{0}$ $E_{n$ 웰 $V_{0}$ 0의 깊이(\ $displaystyle V_{0$ 및 장벽 영역 내 캐리어 유효 질량( $m_{b}^{*}$ b $†\$ 에 따라 달라집니다.

위의 초월 방정식에 대한 해는 숫자 또는 그래픽 방법을 사용하여 쉽게 찾을 수 있습니다.일반적으로 몇 가지 해결책만 있습니다.그러나 최소 하나의 솔루션이 항상 존재하기 때문에 잠재력이 얼마나 작은지에 관계없이 우물 내에 하나의 바인딩 상태가 존재합니다.무한정처럼 우물 안의 파동 함수는 정현파형이지만 우물 장벽에서는 기하급수적으로 붕괴된다.이것은 ^[5]무한정보다 양자정의 결합 에너지 상태를 감소시키는 효과가 있다.

초격자

초격자 구성으로 배열된 AlAs 및 GaAs로 이루어진 헤테로 구조.결과적으로 발생하는 주기적 전위는 재료 간의 밴드갭 차이로 인해 발생합니다.

슈퍼래티스는 서로 다른 밴드갭을 가진 교대로 이루어진 주기적인 헤테로 구조입니다.이러한 주기적 층의 두께는 일반적으로 몇 나노미터 정도 됩니다.이러한 구성에서 발생하는 밴드 구조가 양자 웰의 주기 시리즈입니다.운반선이 여러 유정의 ^[2]장벽 영역을 통과할 수 있을 정도로 이러한 장벽이 충분히 얇아야 한다.초격자의 결정적인 특성은 인접한 유정이 결합할 수 있을 만큼 우물 사이의 장벽이 얇다는 것이다.인접한 파동 기능이 결합하기에는 너무 두꺼운 장벽을 가진 반복된 양자 우물들로 만들어진 주기적 구조는 다중 양자 우물(^[5]MQW) 구조라고 불린다.

반송파가 우물 사이의 장벽 영역을 통해 터널을 뚫을 수 있기 때문에 인접한 유정의 파동 함수는 얇은 장벽을 통해 결합되므로 초격자 상태의 전자적 상태는 비국재적 ^[5]미니밴드를 형성한다.초격자에서 허용되는 에너지 상태에 대한 해법은 구조의 주기성으로 인해 발생하는 경계 조건의 변화가 있는 유한 양자 웰에 대한 해법과 유사하다.전위는 주기적이기 때문에 이 시스템은 1차원 결정 격자와 유사한 방법으로 수학적으로 기술될 수 있다.

적용들

준 2차원적인 성질 때문에, 양자 우물의 전자는 벌크 물질에서 발견되는 매끄러운 제곱근 의존에 비해, 뚜렷한 단계를 가진 에너지의 함수로서 상태의 밀도를 가집니다.또, 원자가 대역의 구멍의 유효 질량을 원자가 대역의 전자와 보다 가깝게 변화시킨다.이 두 가지 요소는 양자 유정의 활성 물질의 감소와 함께 레이저 다이오드와 같은 광학 장치에서의 성능 향상으로 이어집니다.그 결과, 양자 유정은 DVD나 레이저 포인터의 적색 레이저, 광섬유 송신기의 적외선 레이저, 청색 레이저 등 다이오드 레이저에 널리 사용되고 있습니다.그것들은 또한 저소음 전자제품에 사용되는 HEMT(High Electron Mobility Transistors)를 만드는데 사용된다.양자 우물 적외선 광검출기도 양자 우물 기반이며 적외선 이미징에 사용된다.

우물 자체 또는 바람직하게는 양자 우물 장벽 중 하나를 공여 불순물로 도핑함으로써 2차원 전자가스(2DEG)를 형성할 수 있다.이러한 구조는 HEMT의 전도 채널을 만들어 저온에서 흥미로운 특성을 가진다.그러한 특징 중 하나는 높은 자기장에서 볼 수 있는 양자 홀 효과입니다.수용체 도판트는 또한 2차원 홀 가스(2DHG)로 이어질 수 있습니다.

포화 흡수제

양자우물은 그 포화흡수성을 이용하여 포화흡수체로 제작할 수 있다.포화 흡수제는 수동 모드 잠금 레이저에 널리 사용됩니다.반도체 포화 흡수제(SESAM)는 1974년 500ps까지의 펄스를 발생시키는 CO 레이저 모드₂ 잠금에 p형 게르마늄을 사용했을 때 레이저 모드 잠금에 사용되었습니다.최신 SESAM은 III-V 반도체 단일 양자 우물(SQW) 또는 반도체 분산형 브래그 반사체(DBR)에서 성장한 다중 양자 우물(MQW)이다.이들은 처음에는 고속 포화 흡수제로 KLM을 사용한 Ti:sappire 레이저의 시작 메커니즘으로 RPM(Resonance Pulse Modelocking) 체계에서 사용되었습니다.RPM은 또 다른 커플링 캐비티 모드 잠금 기술입니다.펄스 단축을 위해 비공진 Ker형 위상 비선형성을 사용하는 APM 레이저와 달리 RPM은 반도체의 공진 밴드 충전 효과에 의해 제공되는 진폭 비선형성을 사용합니다.SESAM은 이 구조에 내재된 보다 단순성 때문에 곧 내부 포화 흡수 장치로 개발되었습니다.그 후 SESAM을 사용함으로써 초고속 고체 레이저의 펄스 지속 시간, 평균 전력, 펄스 에너지 및 반복 속도를 몇 배 향상할 수 있었습니다.60 W의 평균 전력과 최대 160 GHz의 반복 속도를 얻었습니다.SESAM 지원 KLM을 사용하여 Ti:sappire 발진기에서 직접 sub-6 fs 펄스를 달성했습니다.SESAM이 다른 포화 흡수체 기술에 비해 갖는 주요 장점은 흡수체 매개변수를 광범위한 값에 걸쳐 쉽게 제어할 수 있다는 것입니다.예를 들어 상부 리플렉터의 반사율을 변화시킴으로써 포화 플루언스를 제어하고 흡수체층의 저온 성장 조건을 변화시킴으로써 변조 깊이 및 회복 시간을 조정할 수 있다.이러한 설계의 자유로움은 SESAM을 파이버레이저의 모드 잠금으로 확대하여 자기 기동 및 동작 안정성을 확보하기 위해 비교적 높은 변조 깊이가 필요합니다.최대 1μm 및 1.5μm에서 작동하는 파이버 레이저가 성공적으로 ^[9]시연되었습니다.

열전자학

양자 유정은 열전 소자로써 에너지 수확의 가능성을 보여 왔다.그들은 제작이 더 쉽고 상온에서 작동할 수 있는 가능성을 제공한다고 주장되고 있다.웰은 중앙 캐비티 하나를 두 개의 전자 저장 장치에 연결합니다.중앙 공동은 탱크보다 더 뜨거운 온도로 유지됩니다.유정은 특정 에너지의 전자가 통과할 수 있도록 하는 필터 역할을 합니다.일반적으로 캐비티와 탱크 사이의 온도 차이가 클수록 전자 흐름과 출력 ^[10]^[11]전력이 증가합니다.

실험장치는 1K의 온도차에² 대해 약 0.18W/cm의 출력전력을 공급했는데, 이는 양자 도트 에너지 수확기의 거의 두 배에 해당한다.추가적인 자유도는 더 큰 전류를 허용했다.그 효율은 양자 도트 에너지 하베스터보다 약간 낮다.양자 유정은 특정 수준 이상의 에너지의 전자를 전달하는 반면, 양자 점은 특정 ^[10]에너지의 전자만 통과시킨다.

한 가지 가능한 적용 방법은 컴퓨터 칩의 폐열을 전기 회로로부터 다시 전기로 변환하여 ^[10]칩에 전력을 공급하기 위한 냉각 및 에너지의 필요성을 줄이는 것입니다.

태양 전지

태양 전지의 효율을 높이기 위해 양자 우물이 제안되었다.전통적인 단일 접합 셀의 이론적인 최대 효율은 약 34%인데, 이는 많은 다른 파장의 빛을 포착할 수 없기 때문입니다.직렬로 연결된 여러 밴드갭의 p-n 접합으로 구성된 다중 접합 태양 전지는 흡수된 파장의 범위를 넓힘으로써 이론적인 효율성을 증가시키지만, 그 복잡성과 제조 비용으로 인해 틈새 응용 분야로 사용이 제한된다.한편 고유영역이 하나 이상의 양자웰을 포함하는 p-i-n 접합으로 이루어진 셀은 암전류에 걸쳐 광전류를 증가시켜 기존 p-n ^[12]셀에 비해 순효율이 증가한다.우물 깊이 내의 에너지 광자는 우물에서 흡수되어 전자-공 쌍을 생성한다.실온 조건에서는 이러한 광생성 캐리어는 재결합 ^[13]속도보다 더 빨리 유정을 빠져나갈 수 있는 충분한 열에너지를 가지고 있습니다.정교한 다접합 양자 우물 태양 전지는 분자선 에피택시 또는 화학 증기 증착과 같은 층별 증착 기술을 사용하여 제작될 수 있습니다.또한 세포 위에 첨가된 금속 또는 유전체 나노 입자가 입사광을 다양자 웰 내적층 내에 ^[14]갇힌 횡방향 전파 경로로 산란시킴으로써 광흡수를 더욱 증가시키는 것으로 나타났다.

단결합 태양전지

기존의 단일 접합 광전지에서는 ^[15]다이오드를 가로지르는 광전류와 전압의 산물이다.반도체는 밴드갭보다 높은 에너지를 가진 광자만 흡수하기 때문에 작은 밴드갭 물질은 태양 복사 스펙트럼을 더 많이 흡수하여 더 큰 전류를 발생시킨다.달성 가능한 최고 개방 전압은 ^[15]재료의 내장 밴드갭입니다.반도체의 밴드갭이 전류와 전압을 모두 결정하므로 태양전지 설계는 항상 낮은 밴드갭으로 전류 출력을 최대화하는 것과 높은 ^[16]밴드갭으로 전압 출력을 최대화하는 것의 트레이드오프입니다.기존 태양 전지의 최대 효율 이론 한계는 31%^[15]에 불과하며, 최상의 실리콘 장치는 25%의 최적 한계를 달성합니다.

양자정(QW) 도입으로 단일 접합 변형 QW 실리콘 소자의 효율 한계가 28.3%^[15]로 높아졌다.이러한 증가는 내장 전압을 결정하는 장벽 재료의 밴드갭에 기인합니다.한편, QW의 밴드갭이 흡수 ^[15]한계를 결정합니다.P-i-n 접합 포토다이오드에 대한 실험을 통해, Barnham의 그룹은 QW를 고갈된 영역에 배치하면 ^[17]장치의 효율성이 증가한다는 것을 보여주었다.이에 따라 흡수 스펙트럼에 더 낮은 에너지가 포함되어 새로운 캐리어의 생성과 광전류가 양자 유정에 갇힌 캐리어의 재결합으로 인한 단자 전압의 저하보다 크다는 것이 연구진의 추론이다.추가 연구는 광전류 증가가 흡수 ^[17]스펙트럼의 적색 이동과 직접 관련이 있다는 결론을 내릴 수 있었다.

다접합 태양전지

현재 비QW 태양전지 중 III/V 다접합 태양전지가 가장 효율적이며, 높은 태양광 농도 하에서 최대 46%의 효율을 기록하고 있다.다중 접합 태양 전지는 서로 다른 ^[8]밴드갭의 여러 p-i-n 접합을 쌓음으로써 만들어집니다.태양 전지의 효율은 다른 대역의 QW를 더 많이 도입함으로써 흡수 스펙트럼에 더 많은 태양 복사가 포함됨에 따라 증가한다.밴드갭과 격자상수 사이의 직접적인 관계는 다접합 태양전지의 발전을 방해한다.더 많은 양자 우물(QW)이 함께 성장함에 따라 재료는 다양한 격자 상수로 인해 전위와 함께 성장합니다.전위는 확산 길이와 반송파 ^[8]수명을 감소시킵니다.따라서, QW는 결정 이탈을 최소화하면서 다중 접합 태양 전지에 대한 대체 접근법을 제공한다.

밴드갭 에너지

연구진은 QW를 이용해 결정 이탈을 최소화한 고품질 물질을 배양하고 광흡수와 캐리어 포집 효율을 높여 QW 태양전지를 실현하는 방안을 모색하고 있다.밴드갭 튜너빌리티는 연구자들이 태양전지를 설계하는 데 도움을 준다.QW의 밴드갭 에너지와 입체 변형으로 인한 밴드갭 에너지의 변화로 유효한 밴드갭을 추정할 수 있습니다. 즉, 양자 구속 스타크 효과(QCSE)와 양자 크기 효과(QSE)^[8]입니다.

\displaystyle E_{G, {\text{Eff}}=E_{G}^{\text{well, relaxed}+\delta E_{G}^{\text{G}+\Delta E_{G}^{\text{Q}SE}}+\Delta E_{G}^{\text{Q}CSE}}}

재료의 변형은 밴드갭 에너지에 두 가지 영향을 미칩니다.첫째, 전도 및 원자가 대역의 상대 에너지 변화입니다.이 에너지 변화는 변형률 $\epsilon$ {\ $displaystyle \epsilon$ 탄성강성계수, $C_{11}$ 11 $C_{11}$ {\ $displaystyle C_{11}$ $C_{12}$ C $(\$ 및 정수적 변형 $가능성$ (\ $displaystyle$ a $a$ ^[8]^[18]의 영향을 받습니다.

\displaystyle \Delta E=-2a\left({\frac {C_{11}-C_{12}})\epsilon }

둘째, 이 스트레인에 의해 무거운 구멍과 빛 구멍의 퇴화가 분할된다.중압축재료에서는 중공(hh)이 고에너지 상태로 이동한다.인장재료에서는 광공(lh)이 높은 에너지 상태로 ^[8]^[19]이동한다.전단변형전위 $(\displaystyle$ b $b$ 변형률 $,$ $\epsilon$ (\ $displaystyle \epsilon$ 및 탄성강성계수 $(\$ $(\$ ^[19]로부터 $C_{{11}}$ hh와 lh의 분리에 따른 에너지 차이를 계산할 수 있다.

\displaystyle \Delta E_{h}=b\left({\frac {C_{11}+2C_{12}}{C_{11}\right})\epsilon }

\displaystyle \Delta E_{lh}=-b\left({\frac {C_{11}+2C_{12}}{C_{11}}\right}\epsilon })

양자 구속 스타크 효과는 밴드갭에서 웰 두께 의존적 이동을 유도한다.q $(\displaystyle$ q)가 $q$ 소자 $L_{\text{eff,CB}}$ 인 $경우$ , $L_{\text{eff,CB}}$ (\ $displaystyle L_{\text{eff,$ $CB}}$ $L_{\text{eff,VB}}$ $(\$ L_ ${\text{eff})$ $VB}}$ 는 $L_{\text{eff,VB}}$ 전도 대역과 원자가 대역에서 각각 QW의 유효폭이며 $,$ $F$ ({ $displaystyle$ F $})$ 는 $F$ 압전 편광 및 자연 편광에 의한 유도 전계이며, $δ({$ displaystyle \ $hbar$ 는 플랑크의 감소된 상수이며, 에너지 이동은 다음과 같습니다.^[8]

\displaystyle \Delta E_{G}^{\text{Q}CSE}}=\left({\frac {15-\pi ^{2}}{24\pi ^{2}}\오른쪽)\frac {m_{e}^*}L_{\text{eff},CB}}^{4}+m_{h}^{*}L_{\text{eff,VB}}^{4}{\hbar^{2}}\right)qF^{2}}

양자 크기 효과(QSE)는 전하 캐리어의 Bohr 반경이 우물 크기보다 클 때 제한으로 인해 발생하는 에너지의 이산화입니다.양자 우물 두께가 증가함에 따라 QSE는 감소합니다.QSE의 감소로 인해 n $=$ $n=1$ (\ $displaystyle n=1)$ 상태가 $n=1$ $n=1$ 로 이동하고 유효 밴드갭이 ^[8]감소합니다.크로니그-페니 모델은 양자 ^[20]상태를 계산하기 위해 사용되고 앤더슨의 법칙은 ^[21]에너지에서 전도 대역과 원자가 대역 오프셋을 추정하기 위해 적용된다.

상단: 전하 캐리어의 열전자 누출, 하단:충전 캐리어 터널링

캐리어 캡처 및 라이프 타임

QW에서 캐리어를 효과적으로 사용하면 연구자들은 양자 우물 태양전지(QWSC)의 효율성을 높일 수 있다.p-i-n 태양전지의 고유영역의 QW 내에서 광학적으로 생성된 캐리어는 내장필드에 의해 수집되거나 캐리어 ^[8]재조합에 의해 손실된다.캐리어 재결합은 구멍과 전자가 재결합해 전하를 제거하는 과정이다.전기장에 의한 드리프트를 통해 캐리어를 모을 수 있습니다.얇은 우물이나 열전자 방출로 운반선을 이용할 수도 있고 터널링을 통해 얇은 장벽이나 운반선을 이용할 수도 있다.

탈출용 캐리어 수명은 터널링 및 열전자 방출 수명에 의해 결정된다.터널링 및 열전자 방출 수명은 모두 낮은 유효 장벽 높이에 의존합니다.이것들은 ^[8]^[22]다음 방정식을 통해 표현됩니다.

displaystyle {frac {1} {\text {tun}을(를)}}}}}=pic frac {n\pi \hbar }{2t_{w}^{{w}{*}}e^{\frac {-2}{\hbar}}}\int _{0}^{t_{b}{*}{\pi \harrt {2m_{b}^{*}-E(z}}}}}}}}}}z}}}}}}e^{\frac {2}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

{\frac {1}{\tau _{\text{therm.}}}}={\frac {1}{t_{w}}}{\sqrt {\frac {kT}{2\pi m_{w}^{*}}}}e^{-{\frac {E_{b}}{kT}}}

{\frac {1}{\tau _{\text{therm.}}}}={\frac {1}{t_{w}}}{\sqrt {\frac {kT}{2\pi m_{w}^{*}}}}e^{-{\frac {E_{b}}{kT}}}

}}}}}=black {1}{t_{w}}{\blackrt

T}{2\pi m_{w}^{*}}}}} e^{-{\frac {E_{b}}}{k

T

$m_{b}^{*}$ 서 m b $m_{b}^{*}$ {\({ $displaystyle m_{b}^*})$ $m_{w}^{*}$ $m_{w}^{*}$ w $m_{w}^{*}$ ({ $displaystyle m_{$ w}^*})는 $m_{b}^{*}$ $m_{w}^{*}$ 장벽 $E(z)$ 내의 효과적인 전하 운반체 덩어리이며, $E_{b}$ $E(z)$ displaystyle $E_{b})$ 는 $E_{b}$ 유효 장벽 높이, E $(z)$ 는 전기장입니다.

다음으로 다음과 ^[8]^[22]같이 이스케이프 라이프 타임을 계산할 수 있습니다.

\displaystyle\frac{1}\text\esc.}}}}}=syslogfrac {1}{\syslog_{\text{tun}.}}}}}+{\frac {1}{\flac_{\text{flac}}.}}}}}

소수 캐리어들이 QW에서 탈출할 수 있는 총 확률은 각 유정의 확률의 합이다.

=

P_{i}^{N

^[22]

$P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ 서, $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ 1 $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ . $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ esc $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ + 1 $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ rec $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ $P_{i}=frac {1}{\displaystyle_{\text{esc$ $}}}}{\frac {1}{\frac_{\text{$ $}}}}}+{\frac {1}{\frac_{\text{$ $P_{i}={\frac {\frac {1}{\tau _{\text{esc.}}}}{{\frac {1}{\tau _{\text{esc.}}}}+{\frac {1}{\tau _{\text{rec.}}}}}}$ ^[22] $\tau _{\text{rec.}}$ 서 $\tau _{\text{rec.}}$ 는 rec. $\displaystyle \text{rec.$ $}}$ 은 $\tau _{\text{rec.}}$ (는) 재조합 수명이며 $,$ N(\ $displaystyle$ N $)$ 은 고유 영역의 총 QW 수입니다.

§ $\tau _{\text{esc.}}\ll \tau _{rec.}$ 의 경우. $r$ $}}\ll \ll _{$ $\tau _{\text{esc.}}\ll \tau _{rec.}$ 캐리어 회수가 발생할 가능성이 높습니다 $.$ 이 모델링 방법에서는 각 캐리어가N개의 QW를 $N$ $교차하는$ 반면 실제로는 서로 $다른$ 수의 QW를 교차하는 것으로 가정하고 캐리어 캡처가 100%로 되어 있는 것이 높은 백그라운드 ^[8]도핑 조건에서는 해당되지 않을 수 있습니다.

예를_0.18_0.82 들어, InGaAs ( $\mathrm {\AA}$ {\ \ $displaystyle$ \ $mathrm )$ 를 사용합니다. $AA}$ })/ $\mathrm {\AA}$ GaAsP_0.36_0.64( $\$ $AA}$ 는 고려사항, 터널링, 열전자 방출 수명은 각각 0.89와 1.84이다.재조합 시간을 50ns로 가정해도 단일 양자 우물 및 100 양자 우물 탈출 확률은 0.984와 0.1686으로 효율적인 캐리어 ^[8]포획에는 충분하지 않다.장벽 두께를 20옹스트롬으로 줄이면 $\tau _{\text{tun.}}$ tun이 감소합니다. ${\displaystyle\text{$ $}}~$ 4 $\tau _{\text{tun.}}$ .1276ps로 100QW 이상의 이스케이프 확률이 0.9918로 높아집니다.보다 효율적인 캐리어 ^[8]수집을 위해서는 Thin-Barrier를 사용하는 것이 필수적입니다.

성능에 비추어 벌크 재료 대비 양자 우물 장치의 지속 가능성

Sayed ^[8]등은 1.1~1.3eV 범위에서 Spectrolab에^[23] 의한 Ge 기판상의 변성 InGaAs 벌크 서브셀의 외부 양자효율(EQE)을 100주기_0.30_0.70 InGaAs(3.5nm)/GaAs(2.7nm)/GaAs_0.60_0.40(03)와 비교한다.벌크 머티리얼은 880~900nm 영역의 QW보다 높은EQE 값을 나타내며 QW는 400~600nm 범위의 ^[8]EQE 값을 나타냅니다.이 결과는 변형률 균형 및 반송파 전송 문제로 인해 QW의 흡수 임계값을 더 긴 파장으로 확장하는 데 어려움이 있다는 몇 가지 증거를 제공합니다.그러나 벌크 소재는 변형이 심하여 소수 캐리어 수명이 ^[8]짧습니다.

1.6~1.8 eV 범위에서 Sayed에^[8] 의한 격자 매칭 AlGaAs 및 ^[25]Jain ^[26]등에 의한 InGaAsP와 Sayed에 의한 격자 매칭 InGaAsP/InGaP QW 구조를 비교한다.^[27]1.1~1.3eV 범위와 마찬가지로 벌크 물질의 EQE는 스펙트럼의 긴 파장 영역에서 더 높지만 QW는 스펙트럼의 넓은 영역을 흡수한다는 점에서 유리하다.또, 저온에서 재배할 수 있어 ^[8]열화를 방지할 수 있다.

많은 장치에 양자 유정을 적용하는 것은 그러한 장치의 에너지 효율을 높이기 위한 실행 가능한 해결책이다.레이저를 사용하면 LED와 같은 중요한 결과를 얻을 수 있습니다.QWSC가 태양으로부터 에너지를 수집함에 따라 태양의 방사선을 더 많이 흡수할 수 있고 전하 운반체로부터 그러한 에너지를 더 효율적으로 포착할 수 있게 됨으로써 에너지를 재배하는 더 강력한 방법이 되었습니다.QWSC와 같은 실행 가능한 옵션은 대중들에게 온실 가스 유도 방법에서 더 친환경적인 대안인 태양 에너지로 전환할 수 있는 기회를 제공한다.

「」를 참조해 주세요.

상자 안의 입자
양자선, 운반체들이 2차원에 갇혔어
퀀텀닷, 운반체들이 3차원 모두에 갇혔어
양자 우물 레이저
변조 역반사기

레퍼런스

^ "Quantum Well Infrared Photon Detectors IRnova". www.ir-nova.se. Retrieved 2018-09-04.
^ ^a ^b Odoh, E.O., & Njapba, A.S. (2015년)반도체 양자 우물 소자의 리뷰.어드밴스, 물리 이론이야. 애플, 46, 26-32
^ Kroemer, H. (1963). "A proposed class of hetero-junction injection lasers". Proceedings of the IEEE. Institute of Electrical and Electronics Engineers (IEEE). 51 (12): 1782–1783. doi:10.1109/proc.1963.2706. ISSN 0018-9219.
^ Zh. I. Alferov 및 R.F. Kazarinov, 저자 증명서 28448(US.S.R) 1963.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Fox, Mark; Ispasoiu, Radu (2006), "Quantum Wells, Superlattices, and Band-Gap Engineering", Springer Handbook of Electronic and Photonic Materials, Springer US, pp. 1021–1040, doi:10.1007/978-0-387-29185-7_42, ISBN 978-0-387-26059-4
^ ^a ^b Nag, B. R. (2002). Physics of quantum well devices. Kluwer Academic Publishers. OCLC 754036669.
^ ^a ^b Simon, Steven H. (2017). The Oxford solid state basics. Oxford University Press. ISBN 978-0-19-968077-1. OCLC 1091723162.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v Sayed, Islam; Bedair, S. M. (2 March 2019). "Quantum Well Solar Cells: Principles, Recent Progress, and Potential". IEEE Journal of Photovoltaics. 9 (2): 402–423. doi:10.1109/JPHOTOV.2019.2892079. ISSN 2156-3381. S2CID 67874610.
^ Tang, D.; Zhang, H.; Zhao, L.; Wu, X. (2008). "Observation of High-Order Polarization-Locked Vector Solitons in a Fiber Laser" (PDF). Physical Review Letters. 101 (15): 153904. arXiv:0903.2392. Bibcode:2008PhRvL.101o3904T. doi:10.1103/PhysRevLett.101.153904. PMID 18999601. S2CID 35230072. Archived from the original (PDF) on January 20, 2010.
^ ^a ^b ^c "Scientists propose quantum wells as high-power, easy-to-make energy harvesters". Phys.org. Retrieved 2013-10-24.
^ Sothmann, B. R.; Sánchez, R.; Jordan, A. N.; Büttiker, M. (2013). "Powerful energy harvester based on resonant-tunneling quantum wells". New Journal of Physics. 15 (9): 095021. arXiv:1309.7907. Bibcode:2013NJPh...15i5021S. doi:10.1088/1367-2630/15/9/095021. S2CID 119210320.
^ Barnham, K.; Zachariou, A. (1997). "Quantum well solar cells". Applied Surface Science. 113–114: 722–733. Bibcode:1997ApSS..113..722B. doi:10.1016/S0169-4332(96)00876-8.
^ Ramey, S. M.; Khoie, R. (2003). "Modeling of multiple-quantum-well solar cells including capture, escape, and recombination of photoexcited carriers in quantum wells". IEEE Transactions on Electron Devices. 50 (5): 1179–1188. Bibcode:2003ITED...50.1179R. doi:10.1109/TED.2003.813475.
^ Derkacs, D.; Chen, W. V.; Matheu, P. M.; Lim, S. H.; Yu, P. K. L.; Yu, E. T. (2008). "Nanoparticle-induced light scattering for improved performance of quantum-well solar cells". Applied Physics Letters. 93 (9): 091107. Bibcode:2008ApPhL..93i1107D. doi:10.1063/1.2973988.
^ ^a ^b ^c ^d ^e Fox, Mark; Ispasoiu, Radu (2017), Kasap, Safa; Capper, Peter (eds.), "Quantum Wells, Superlattices, and Band-Gap Engineering", Springer Handbook of Electronic and Photonic Materials, Springer International Publishing, p. 1, doi:10.1007/978-3-319-48933-9_40, ISBN 978-3-319-48931-5
^ Barnham, Keith; Ballard, Ian; Barnes, Jenny; Connolly, James; Griffin, Paul; Kluftinger, Benjamin; Nelson, Jenny; Tsui, Ernest; Zachariou, Alexander (1997-04-01). "Quantum well solar cells". Applied Surface Science. Proceedings of the Eighth International Conference on Solid Films and Surfaces. 113–114: 722–733. Bibcode:1997ApSS..113..722B. doi:10.1016/S0169-4332(96)00876-8. ISSN 0169-4332.
^ ^a ^b Anderson, Neal G. (13 April 1995). "Ideal theory of quantum well solar cells". Journal of Applied Physics. 78 (3): 1850–1861. Bibcode:1995JAP....78.1850A. doi:10.1063/1.360219. ISSN 0021-8979.
^ Asai, Hiromitsu; Oe, Kunishige (1983). "Energy band‐gap shift with elastic strain in GaxIn1−xP epitaxial layers on (001) GaAs substrates". Journal of Applied Physics. 54 (4): 2052–2056. doi:10.1063/1.332252. ISSN 0021-8979.
^ ^a ^b Adachi, Sadao (1982). "Material parameters of In1−xGaxAsyP1−yand related binaries". Journal of Applied Physics. 53 (12): 8775–8792. doi:10.1063/1.330480. ISSN 0021-8979.
^ "Quantum Wires and Dots", Quantum Wells, Wires and Dots, John Wiley & Sons, Ltd, 2006-01-27, pp. 243–270, doi:10.1002/0470010827.ch8, ISBN 978-0-470-01082-2
^ Anderson, R. L. (1960). "Germanium-Gallium Arsenide Heterojunctions [Letter to the Editor]". IBM Journal of Research and Development. 4 (3): 283–287. doi:10.1147/rd.43.0283. ISSN 0018-8646.
^ ^a ^b ^c ^d Nelson, J.; Paxman, M.; Barnham, K.W.J.; Roberts, J.S.; Button, C. (June 1993). "Steady-state carrier escape from single quantum wells". IEEE Journal of Quantum Electronics. 29 (6): 1460–1468. Bibcode:1993IJQE...29.1460N. doi:10.1109/3.234396. ISSN 0018-9197.
^ King, R., Law, D., Fetzer, C., Sherif, R., Edmondson, K., Kurtz, S.... 및 Karam, N. H. (2005년, 6월)40% 효율의 집광기 태양광 발전 경로.제20회 유럽 태양광 발전 태양 에너지 회의 (pp. 10-11).
^ Fujii, Hiromasa; Toprasertpong, Kasidit; Wang, Yunpeng; Watanabe, Kentaroh; Sugiyama, Masakazu; Nakano, Yoshiaki (2014). "100-period, 1.23-eV bandgap InGaAs/GaAsP quantum wells for high-efficiency GaAs solar cells: Toward current-matched Ge-based tandem cells". Progress in Photovoltaics: Research and Applications. 22 (7): 784–795. doi:10.1002/pip.2454.
^ Heckelmann, Stefan; Lackner, David; Karcher, Christian; Dimroth, Frank; Bett, Andreas W. (2015). "Investigations on Al_xGa_1-xAs Solar Cells Grown by MOVPE". IEEE Journal of Photovoltaics. 5 (1): 446–453. doi:10.1109/jphotov.2014.2367869. S2CID 41026351.
^ Jain, Nikhil; Geisz, John F.; France, Ryan M.; Norman, Andrew G.; Steiner, Myles A. (2017). "Enhanced Current Collection in 1.7 eV GaInAsP Solar Cells Grown on GaAs by Metalorganic Vapor Phase Epitaxy". IEEE Journal of Photovoltaics. 7 (3): 927–933. doi:10.1109/jphotov.2017.2655035. OSTI 1360894. S2CID 20841656.
^ Sayed, Islam E. H.; Jain, Nikhil; Steiner, Myles A.; Geisz, John F.; Bedair, S. M. (2017). "100-period InGaAsP/InGaP superlattice solar cell with sub-bandgap quantum efficiency approaching 80%". Applied Physics Letters. 111 (8): 082107. Bibcode:2017ApPhL.111h2107S. doi:10.1063/1.4993888. OSTI 1393377.

추가 정보

토마스 엥겔, 필립 리드 양자 화학 및 분광학.ISBN 0-8053-3843-8.Pearson Education, 2006.73~75페이지.

[1] "Quantum Well Infrared Photon Detectors IRnova". www.ir-nova.se. Retrieved 2018-09-04.

[:3-2] Odoh, E.O., & Njapba, A.S. (2015년)반도체 양자 우물 소자의 리뷰.어드밴스, 물리 이론이야. 애플, 46, 26-32

[kroemer-3] Kroemer, H. (1963). "A proposed class of hetero-junction injection lasers". Proceedings of the IEEE. Institute of Electrical and Electronics Engineers (IEEE). 51 (12): 1782–1783. doi:10.1109/proc.1963.2706. ISSN 0018-9219.

[alferov-4] Zh. I. Alferov 및 R.F. Kazarinov, 저자 증명서 28448(US.S.R) 1963.

[:0-5] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Fox, Mark; Ispasoiu, Radu (2006), "Quantum Wells, Superlattices, and Band-Gap Engineering", Springer Handbook of Electronic and Photonic Materials, Springer US, pp. 1021–1040, doi:10.1007/978-0-387-29185-7_42, ISBN 978-0-387-26059-4

[:2-6] Nag, B. R. (2002). Physics of quantum well devices. Kluwer Academic Publishers. OCLC 754036669.

[:1-7] Simon, Steven H. (2017). The Oxford solid state basics. Oxford University Press. ISBN 978-0-19-968077-1. OCLC 1091723162.

[:4-8] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v Sayed, Islam; Bedair, S. M. (2 March 2019). "Quantum Well Solar Cells: Principles, Recent Progress, and Potential". IEEE Journal of Photovoltaics. 9 (2): 402–423. doi:10.1109/JPHOTOV.2019.2892079. ISSN 2156-3381. S2CID 67874610.

[9] Tang, D.; Zhang, H.; Zhao, L.; Wu, X. (2008). "Observation of High-Order Polarization-Locked Vector Solitons in a Fiber Laser" (PDF). Physical Review Letters. 101 (15): 153904. arXiv:0903.2392. Bibcode:2008PhRvL.101o3904T. doi:10.1103/PhysRevLett.101.153904. PMID 18999601. S2CID 35230072. Archived from the original (PDF) on January 20, 2010.

[phys1013-10] "Scientists propose quantum wells as high-power, easy-to-make energy harvesters". Phys.org. Retrieved 2013-10-24.

[11] Sothmann, B. R.; Sánchez, R.; Jordan, A. N.; Büttiker, M. (2013). "Powerful energy harvester based on resonant-tunneling quantum wells". New Journal of Physics. 15 (9): 095021. arXiv:1309.7907. Bibcode:2013NJPh...15i5021S. doi:10.1088/1367-2630/15/9/095021. S2CID 119210320.

[12] Barnham, K.; Zachariou, A. (1997). "Quantum well solar cells". Applied Surface Science. 113–114: 722–733. Bibcode:1997ApSS..113..722B. doi:10.1016/S0169-4332(96)00876-8.

[13] Ramey, S. M.; Khoie, R. (2003). "Modeling of multiple-quantum-well solar cells including capture, escape, and recombination of photoexcited carriers in quantum wells". IEEE Transactions on Electron Devices. 50 (5): 1179–1188. Bibcode:2003ITED...50.1179R. doi:10.1109/TED.2003.813475.

[14] Derkacs, D.; Chen, W. V.; Matheu, P. M.; Lim, S. H.; Yu, P. K. L.; Yu, E. T. (2008). "Nanoparticle-induced light scattering for improved performance of quantum-well solar cells". Applied Physics Letters. 93 (9): 091107. Bibcode:2008ApPhL..93i1107D. doi:10.1063/1.2973988.

[:5-15] Fox, Mark; Ispasoiu, Radu (2017), Kasap, Safa; Capper, Peter (eds.), "Quantum Wells, Superlattices, and Band-Gap Engineering", Springer Handbook of Electronic and Photonic Materials, Springer International Publishing, p. 1, doi:10.1007/978-3-319-48933-9_40, ISBN 978-3-319-48931-5

[16] Barnham, Keith; Ballard, Ian; Barnes, Jenny; Connolly, James; Griffin, Paul; Kluftinger, Benjamin; Nelson, Jenny; Tsui, Ernest; Zachariou, Alexander (1997-04-01). "Quantum well solar cells". Applied Surface Science. Proceedings of the Eighth International Conference on Solid Films and Surfaces. 113–114: 722–733. Bibcode:1997ApSS..113..722B. doi:10.1016/S0169-4332(96)00876-8. ISSN 0169-4332.

[:6-17] Anderson, Neal G. (13 April 1995). "Ideal theory of quantum well solar cells". Journal of Applied Physics. 78 (3): 1850–1861. Bibcode:1995JAP....78.1850A. doi:10.1063/1.360219. ISSN 0021-8979.

[18] Asai, Hiromitsu; Oe, Kunishige (1983). "Energy band‐gap shift with elastic strain in GaxIn1−xP epitaxial layers on (001) GaAs substrates". Journal of Applied Physics. 54 (4): 2052–2056. doi:10.1063/1.332252. ISSN 0021-8979.

[:7-19] Adachi, Sadao (1982). "Material parameters of In1−xGaxAsyP1−yand related binaries". Journal of Applied Physics. 53 (12): 8775–8792. doi:10.1063/1.330480. ISSN 0021-8979.

[20] "Quantum Wires and Dots", Quantum Wells, Wires and Dots, John Wiley & Sons, Ltd, 2006-01-27, pp. 243–270, doi:10.1002/0470010827.ch8, ISBN 978-0-470-01082-2

[21] Anderson, R. L. (1960). "Germanium-Gallium Arsenide Heterojunctions [Letter to the Editor]". IBM Journal of Research and Development. 4 (3): 283–287. doi:10.1147/rd.43.0283. ISSN 0018-8646.

[:8-22] Nelson, J.; Paxman, M.; Barnham, K.W.J.; Roberts, J.S.; Button, C. (June 1993). "Steady-state carrier escape from single quantum wells". IEEE Journal of Quantum Electronics. 29 (6): 1460–1468. Bibcode:1993IJQE...29.1460N. doi:10.1109/3.234396. ISSN 0018-9197.

[23] King, R., Law, D., Fetzer, C., Sherif, R., Edmondson, K., Kurtz, S.... 및 Karam, N. H. (2005년, 6월)40% 효율의 집광기 태양광 발전 경로.제20회 유럽 태양광 발전 태양 에너지 회의 (pp. 10-11).

[24] Fujii, Hiromasa; Toprasertpong, Kasidit; Wang, Yunpeng; Watanabe, Kentaroh; Sugiyama, Masakazu; Nakano, Yoshiaki (2014). "100-period, 1.23-eV bandgap InGaAs/GaAsP quantum wells for high-efficiency GaAs solar cells: Toward current-matched Ge-based tandem cells". Progress in Photovoltaics: Research and Applications. 22 (7): 784–795. doi:10.1002/pip.2454.

[25] Heckelmann, Stefan; Lackner, David; Karcher, Christian; Dimroth, Frank; Bett, Andreas W. (2015). "Investigations on Al_xGa_1-xAs Solar Cells Grown by MOVPE". IEEE Journal of Photovoltaics. 5 (1): 446–453. doi:10.1109/jphotov.2014.2367869. S2CID 41026351.

[26] Jain, Nikhil; Geisz, John F.; France, Ryan M.; Norman, Andrew G.; Steiner, Myles A. (2017). "Enhanced Current Collection in 1.7 eV GaInAsP Solar Cells Grown on GaAs by Metalorganic Vapor Phase Epitaxy". IEEE Journal of Photovoltaics. 7 (3): 927–933. doi:10.1109/jphotov.2017.2655035. OSTI 1360894. S2CID 20841656.

[27] Sayed, Islam E. H.; Jain, Nikhil; Steiner, Myles A.; Geisz, John F.; Bedair, S. M. (2017). "100-period InGaAsP/InGaP superlattice solar cell with sub-bandgap quantum efficiency approaching 80%". Applied Physics Letters. 111 (8): 082107. Bibcode:2017ApPhL.111h2107S. doi:10.1063/1.4993888. OSTI 1393377.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[25]

[26]

[27]

v t 양자역학
배경	서론 역사 타임라인 고전 역학 구 양자론 용어집
기초	타고난 규칙 브라켓 표기법 상보성 밀도 매트릭스 에너지 레벨 접지 상태 들뜬 상태 퇴화 수준 제로 포인트 에너지 얽힘 해밀턴식 방해다 데코히렌스 측정. 비국소성 양자 상태 중첩 터널링 산란 이론 양자역학에서의 대칭성 불확실성 파동 함수 접다 파동-입자 이중성
제제	제제 하이젠베르크 상호 작용 행렬 역학 슈뢰딩거 경로 적분 공식 위상 공간
방정식	디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석	해석 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션 폰 노이만 위그너
실험	벨 부등식 데이비슨-게르머 선택 지연 양자 지우개 더블 슬릿 프랑크-헤르츠 마하-젠더 간섭계 엘리추르-바이드만 포퍼 양자 지우개 스턴-게라크 Wheeler의 지연
과학	양자생물학 양자 화학 양자 카오스 양자 우주론 양자 미분학 양자역학 양자 기하학 양자 측정 문제 양자 확률 미적분 양자 시공간
테크놀로지	양자 알고리즘 양자 증폭기 양자 버스 양자 세포 오토마타 양자 유한 오토마타 양자 채널 양자 회로 양자 복잡도 이론 양자 컴퓨팅 타임라인 양자암호학 양자 전자 공학 양자 오차 보정 양자 이미징 양자 이미지 처리 양자 정보 양자 키 배포 양자 논리 양자 논리 게이트 양자 기계 양자 기계 학습 양자 메타물질 양자 도량형 양자 네트워크 양자 신경망 양자 광학 양자 프로그래밍 양자 감지 양자 시뮬레이터 양자 순간이동
내선번호	카시미르 효과 양자통계역학 양자장론 역사 양자 중력 상대론적 양자역학
관련된	슈뢰딩거의 고양이 대중문화에서. 양자 신비주의
카테고리 물리 포털 공통

Search

양자 우물

네임스페이스

더

목차

역사

제조

설명 및 개요

물리

무한 우물 모형

솔루션 및 에너지 수준

유한 우물 모형

솔루션 및 에너지 수준

초격자

적용들

포화 흡수제

열전자학

태양 전지

단결합 태양전지

다접합 태양전지

밴드갭 에너지

캐리어 캡처 및 라이프 타임

성능에 비추어 벌크 재료 대비 양자 우물 장치의 지속 가능성

「」를 참조해 주세요.

레퍼런스

추가 정보

Search

양자 우물

역사

제조

설명 및 개요

물리

무한 우물 모형

솔루션 및 에너지 수준

유한 우물 모형

솔루션 및 에너지 수준

초격자

적용들

포화 흡수제

열전자학

태양 전지

단결합 태양전지

다접합 태양전지

밴드갭 에너지

캐리어 캡처 및 라이프 타임

성능에 비추어 벌크 재료 대비 양자 우물 장치의 지속 가능성

「 」를 참조해 주세요.

레퍼런스

추가 정보

「」를 참조해 주세요.