초단파 펄스

광학에서 초고속 이벤트라고도 하는 초단 펄스는 시간 지속 시간이 피코초(10초⁻¹²) 이하인 전자기 펄스입니다.이러한 펄스는 광대역 광학 스펙트럼을 가지며 모드 잠금 발진기에 의해 생성될 수 있습니다.초단파 펄스의 증폭에는 증폭기의 이득 매체의 손상을 방지하기 위해 거의 항상 채프 펄스 증폭 기술이 필요합니다.

일반적으로 공기를 포함한 다양한 재료에서 비선형 상호작용을 일으키는 높은 피크 강도(또는 보다 정확하게는 방사선 강도)가 특징이다.이러한 과정은 비선형 광학 분야에서 연구됩니다.

전문 문헌에서 "초점"은 펨토초(fs) 및 피코초(ps) 범위를 가리키지만, 이러한 펄스는 더 이상 인공적으로 생성된 최단 펄스의 기록을 보유하지 않습니다.실제로 아토초 시간 척도의 지속 시간을 갖는 X선 펄스가 보고되었습니다.

1999년 노벨 화학상은 초단파 펄스를 사용하여 일어나는 시간 단위에서의 화학 반응을 관찰하여 펨토케미스트리 분야를 개방한 공로로 아흐메드 H. 제웨일에게 수여되었습니다.

정의.

시간 영역에 있는 빛의 초단파 펄스가 확실히 차동합니다.

초단파 펄스의 표준 정의는 없습니다.일반적으로 '울트라쇼트' 속성은 수십 펨토초의 지속시간을 갖는 펄스에 적용되지만, 더 큰 의미에서는 몇 피코초 미만으로 지속되는 펄스는 울트라쇼트로 간주될 수 있습니다.펄스가 전파되는 속도는 펄스가 통과하는 매체의 굴절률 함수인 반면, "울트라쇼트"는 펄스 파형 ^[1]패킷의 시간적 폭을 의미하기 때문에 "울트라쇼트"와 "울트라쇼트"의 구별이 필요합니다.

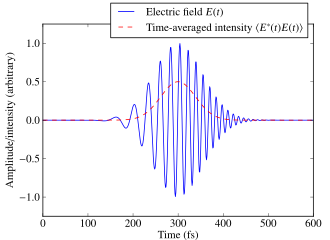
일반적인 예로는 차핑된 가우스 펄스가 있습니다.차핑된 가우스 펄스는 필드 진폭이 가우스 엔벨로프를 따르고 순간 위상이 주파수 스위프를 갖는 파형입니다.

배경

초단펄스에 대응하는 실전계는 펄스의 중심파장에 대응하는 각주파수θ로₀ 진동한다.계산을 용이하게 하기 위해 복잡한 필드 E(t)를 정의한다.형식적으로는 실장에 대응하는 해석 신호로 정의된다.

중심 각도 주파수 θ는₀ 일반적으로 시간 강도 함수 I(t)와 시간 위상 함수 θ(t)로 분리될 수 있는 복합 필드에 명시적으로 작성된다.

E(t)=sqrt {I(t)}} e^{i\obega _{0}t} e^{i\psi(t)}

주파수 영역에서 복잡한 전계의 식은 E(t)의 푸리에 변환에서 얻을 수 있습니다.

E(\mega)=mathcal {F}}(E(t))

$e^{i\omega _{0}t}$ i $e^{i\omega _{0}t}$ $e^{i\omega _{0}t}$ t $e^{i\omega _{0}t}$ { $displaystyle$ e^ { $i$ \ $opega _$ { 0 $}$ t $e^{i\omega _{0}t}$ } 용어가 존재하기 때문에 E(')는₀ ,를 중심으로 하고 있으며, E('-')를₀ E('-')로 표기하는 것이 일반적입니다.이 문서의 뒷부분에서 설명하겠습니다.

시간 영역과 마찬가지로 강도 및 위상 함수를 주파수 영역에서 정의할 수 있습니다.

(\displaystyle E(\obmega)=t{S(\obmega)}} e^{i\phi(\obmega)})}

$S(\omega )$ ( $S(\omega )$ ) { $display S$ ( \ $메가$ )}는 $S(\omega )$ 펄스의 파워 스펙트럼 밀도(또는 단순히 스펙트럼)이며, $\phi (\omega )$ ( $display$ ) { $display$ \phi ( \ $메가$ )는 $\phi (\omega )$ 위상 스펙트럼 밀도(또는 단순히 스펙트럼 위상)입니다.스펙트럼 위상함수의 예로는 $\phi (\omega )$ ( $\phi (\omega )$ $){$ $displaystyle \phi$ ( \ $\phi (\omega )$ 메가 )}가 $\phi (\omega )$ $\phi (\omega )$ 상수인 경우, 또는 $\phi (\omega )$ ( $style$ ){ $displaystyle$ \ $phi$ ( \ $\phi (\omega )$ 메가 )}가 2차 함수인 경우 등이 있으며, 이 경우 펄스는 inst의 존재로 인해 chirped pulse라고 불립니다.자동 주파수 스위프.이러한 진동은 펄스가 물질(유리와 같은 것)을 통해 전파될 때 얻을 수 있으며 그 분산에 기인합니다.맥박이 일시적으로 넓어지는 결과를 낳습니다.

강도 함수( $I(t)$ I $(\displaystyle$ I $($ $S(\omega )$ $))$ 및 $I(t)$ $S(\omega )$ S $S(\omega )$ $))$ { $displaystyle$ S $(\omega)})$ 는 펄스의 시간 지속 시간과 스펙트럼 대역폭을 결정합니다.불확도 원리에 의해 기술된 바와 같이, 그들의 곱(시간대역폭 곱이라고도 함)은 하한을 가진다.이 최소값은 지속 시간 및 펄스의 모양에 따라 달라집니다.주어진 스펙트럼에 대해 최소 시간대역폭 곱, 즉 최단 펄스는 변환제한 펄스에 의해 $\phi (\omega )$ $반면$ 시간대역폭 $곱의 높은$ 값은 보다 복잡한 펄스를 나타낸다 $.$

펄스 형상 제어

빔 익스팬더나 공간 필터와 같은 연속광에도 사용되는 광학 장치를 초단 펄스에 사용할 수 있지만, 일부 광학 장치는 초단 펄스에 맞게 특별히 설계되어 있습니다.그 중 하나는 펄스 압축기로,^[2] 초단파 펄스의 스펙트럼 위상을 제어하는 데 사용할 수 있는 장치입니다.그것은 일련의 프리즘, 즉 격자로 구성되어 있다.적절히 조정하면 입력 펄스의 스펙트럼 위상 δ(θ)를 변경하여 출력 펄스가 가능한 한 짧은 지속시간을 갖는 대역폭 제한 펄스가 되도록 할 수 있습니다.펄스 셰이퍼를 사용하여 초단 펄스의 위상 및 진폭을 보다 복잡하게 변경할 수 있습니다.

펄스를 정확하게 제어하려면 특정 펄스 스펙트럼 위상(변환 제한 등)을 얻기 위해 펄스 스펙트럼 위상의 완전한 특성화가 필요합니다.그런 다음 공간광 변조기를 4f 평면에서 사용하여 펄스를 제어할 수 있습니다.Multihoton IntraPulse Interference Phase Scan(MIPS; 멀티호톤 펄스 내 간섭 위상 스캔)은 이 개념에 기반한 기술입니다.MIPS는 공간 광변조기의 위상 스캔을 통해 초단 펄스를 특성화할 수 있을 뿐만 아니라 목표 지점에서 필요한 펄스 모양(예: 최적화된 피크 전력을 위한 변환 제한 펄스 및 기타 특정 펄스 모양)을 얻도록 조작할 수 있습니다.펄스 셰이퍼가 완전히 보정된 경우 이 기술을 통해 움직이는 부품이 없는 간단한 광학 설정을 사용하여 초단파 펄스의 스펙트럼 위상을 제어할 수 있습니다.단, MIPS의 정확도는 주파수 분해 광학 게이트(FROG)^[3] 등 다른 기술에 대해서는 다소 제한됩니다.

측정 기술

초단파 광펄스를 측정하기 위해 몇 가지 기술을 사용할 수 있습니다.

강도 자기 상관은 특정 펄스 형태를 가정할 때 펄스 폭을 제공합니다.

스펙트럼 간섭계(SI)는 사전 특성화된 기준 펄스를 사용할 수 있을 때 사용할 수 있는 선형 기법이다.그것은 강렬함과 위상을 준다.SI 신호에서 강도와 위상을 추출하는 알고리즘은 직접적입니다.직접 전계 재구성(SPIDER)을 위한 스펙트럼 위상 간섭계는 스펙트럼 전단 간섭계에 기초한 비선형 자기 참조 기술이다.이 방법은 기준 펄스가 스펙트럼으로 이동된 복제품이라는 점을 제외하면 SI와 유사하며, SI와 유사한 직접 FFT 필터링 루틴을 통해 프로브 펄스의 스펙트럼 강도와 위상을 얻을 수 있지만 프로브 펄스 위상을 얻으려면 간섭도에서 추출한 위상을 통합해야 합니다.

FROG(Frequency-Resolved Optical Gating)는 펄스의 강도와 위상을 산출하는 비선형 기술입니다.이것은 스펙트럼적으로 분해된 자기 상관 관계입니다.PROG 트레이스에서 강도 및 위상을 추출하는 알고리즘은 반복적입니다.초고속 입사 레이저광 전자장(GRENOUILE)의 격자 제거 관찰은 FROG의 간략화된 버전입니다(GRENOUILE은 프랑스어로 '개구리'를 의미합니다).

처프 스캔은 2차 스펙트럼 위상의 램프를 적용하고 2차 고조파 스펙트럼을 측정하여 펄스의 스펙트럼 위상을 측정하는 MIPS와 유사한 기법이다.스펙트럼 위상을 측정하기 위해 많은 반복이 필요한 MIPS와 관련하여, 진폭과 ^[4]펄스의 위상을 모두 검색하기 위해 두 번의 차프 스캔만 필요합니다.

멀티호톤 펄스 내 간섭 위상 스캔(MIPS)은 초단파 펄스를 특성화하고 조작하는 방법입니다.

비등방성 미디어에서의 웨이브 패킷 전파

위에서 설명한 내용을 부분적으로 반복하기 위해 중심파 ${\textbf {K}}_{0}$ ${\textbf {K}}_{0}$ 0(\ $displaystyle\textbf$ { $K}}_$ {0})과 ${\textbf {K}}_{0}$ 중심 주파수 $\omega _{0}$ 0 $(\displaystyle\Omega_{0})$ 을 $\omega _{0}$ 갖는 파형의 전계의 느리게 변화하는 포락선 근사(SVEA)는 다음과 같습니다.

\displaystyle {\textbf {E}}({\textbf {x}},t)=txtextbf {A}}({\textbf {x},t})\exp(i\textbf {K}}_{0}-i\textbf {0})

균질 분산형 비등방성 배지에서 전계의 SVEA 전파를 고려한다.펄스가 z축 방향으로 전파된다고 가정하면, 가장 일반적인 사례 중 하나인 2축 결정의 ${\textbf {A}}$ A(\ $displaystyle\textbf$ {A $})$ 가 ${\textbf {A}}$ PDE에 ^[5]의해 제어된다는 것을 알 수 있습니다.

{\frac {textbf {A}} {\frac {textbf {A}} {\frac {i} {\frac {2} {\frac {\textbf {A}} {\frac {\f} {\frac} {\f} {\f} {partial}레이스 {\textbf {A}{\partial y}

~~~~~~~~~~~i\gamma _{tx}{\frac {\partial ^{2}{\textbf {A}}}{\partial x}~+_i\gamma _{ty}{\frac ^{partial ^{2}{\partial {A}}}}}{partial t}}}{\fracial }}y}{\frac {\partial ^{2}{\textbf {A}}{\partial x\partial y}}+\cdots

여기서 계수는 컴퓨터 대수학을 사용하여 분석적으로 결정되고 근접장 및 원거리장에서 유효한 등방성 및 비등방성 매체에 대해 3차 이내로 수치적으로 검증되는 회절 및 분산 효과를 포함한다. $\beta _{1}$ 1 $(\$ _ ${1})$ 은 $\beta _{1}$ 그룹 속도 예측의 역수이다. $\beta _{2}$ 2 $(\$ _ ${2$ })의 $\beta _{2}$ 용어는 그룹 속도 분산(GVD) 또는 2차 분산입니다. 펄스 지속 시간을 늘리고 펄스가 매체를 통해 전파될 때 펄스를 차동합니다. $\beta _{3}$ 3 $({$ _ ${3})$ 의 $\beta _{3}$ 용어는 $\beta _{2}$ 2 $({$ _ ${2})$ 가 $\beta _{2}$ $\beta _{2}$ 펄스 지속 시간을 더욱 늘릴 수 있는 3차 분산 용어입니다.§ $\gamma _{x}$ ( \ $displaystyle$ \ $gamma$ $\gamma _{y}$ _ { $x$ $\gamma _{x}$ } ) $\gamma _{x}~(\gamma _{y})$ $§$ y ( \ $displaystyle$ \ $gamma$ _ { y $\gamma _{y}$ $}$ )의 용어는 펄스의 워크오프를 나타냅니다.계수 $\gamma _{x}~(\gamma _{y})$ x ( \ $displaystyle$ \ $gamma$ _ { $x$ $x~(y)$ } ~\ $gamma$ _ { y $x~(y)$ })는 $\gamma _{x}~(\gamma _{y})$ $x~(y)$ 그룹 $x~(y)$ x ( $y )$ 의 성분 비율입니다.펄스의 전파 보정(z축). $\gamma _{xx}$ $\gamma _{xx}$ \ $gamma _{$ xx $\gamma _{xx}$ }} $\gamma _{yy}$ y ${\displaystyle$ \ $gamma$ _{ $y}}$ 의 $\gamma _{{yy}}$ 용어는 광파 패킷이 전파축에 수직인 방향으로 회절되는 것을 나타냅니다.시공간에서 혼합된 파생물을 포함하는 $\gamma _{ty}$ $\gamma _{tx}$ t $\gamma _{tx}$ \ $displaystyle$ \ $gamma$ _ { $ty$ } 및 $\gamma _{tx}$ $\gamma _{ty}$ t $\gamma _{ty}$ \ $displaystyle$ $\ gamma$ _ { $ty}$ 의 항은 각각 $y축$ 과 $y$ $\$ $displaystyle$ x축에 $x$ 대해 파형 패킷을 회전시켜 파형 패킷의 시간 폭을 증가시킵니다(du 증가).e에서 GVD로)의 $경우$ x $(\displaystyle$ x $)$ $y$ 과 $x$ $y$ (\ $displaystyle$ y) 방향의 $y$ 분산을 각각 증가시키고 chirp(β $\beta _{2}$ (\ $displaystyle \beta$ _ ${2$ 에 의해 chirp를 증가시킵니다(\ $displaystyle \gamma$ _ ${xxxxxxxxxx$ $}$ 및 $\gamma _{yy}$ $}).$ 사라지지 않는다.용어 " $\gamma _{xy}$ y \ $displaystyle \gamma$ _ ${xy}"$ 는 $\gamma _{{xy}}$ $x-y$ $x-y$ - $x-y$ \ $displaystyle x-y$ 평면에서 파형 패킷을 회전시킵니다.이상하게도, 이전에 불완전한 팽창 때문에, 이 펄스의 회전이 1990년대 후반까지 실현되지 않았지만 실험적으로 확인되었다.^[6]세 번째 순서로, 위의 방정식의 RHS에는 단축 결정 ^[7]케이스에 대한 다음과 같은 추가 항이 있습니다.

\cdots ~+~{\frac {1}{3}\gamma _{tx}{\frac {A}}{\partial x^{2}\textbf {A}}}{\partial t}~+{\frac {1}{3}\gamma _{ty}{\fartial ^{\f

첫 번째 항과 두 번째 항은 펄스 전반 전선의 곡률을 담당합니다. $\beta _{3}$ 3 $(\$ _ ${3})$ 의 $\beta _{3}$ 용어를 포함한 이러한 용어는 등방성 매체에 존재하며 점 선원에서 유래한 전파 전선의 구형 표면을 설명한다. $,$ 주파수 $\omega$ \ $displaystyle\gamma_$ ${tx}$ 와 $\gamma _{{txx}}$ $\omega$ 그 도함수로 표현될 수 있으며 $\gamma _{ttx}$ $\gamma _{ttx}$ { $tx}$ 도 펄스를 왜곡하지만 t $\displaystyle\$ $gamma_{ttx$ }의 $\gamma _{ttx}$ $t$ $t$ 을 역전시키는 방식으로 표현된다. $($ 내용은 Trippenbach, Scott 및 Band 참조).지금까지, 여기서의 처리는 선형이지만, 비선형 분산 용어는 자연 어디에나 존재한다. $\gamma _{nl}|A|^{2}A$ 인 비선형 용어 § $\gamma _{nl}|A|^{2}A$ $\gamma _{nl}|A|^{2}A$ $\gamma _{nl}|A|^{2}A$ $\gamma _{nl}|A|^{2}A$ A $(\displaystyle \gamma$ _ ${nl} A ^{2}A)$ 와 $\gamma _{{nl}}|A|^{2}A$ 관련된 연구는 그러한 용어들이 파형 ^[8]패킷의 자기 스티핑(self-stepping)을 포함하여 파형 패킷에 큰 영향을 미친다는 것을 보여주었습니다.비선형 측면은 결국 광학 솔리톤으로 이어집니다.

비교적 일반적이지만 SVEA는 광펄스의 전파를 설명하는 단순한 파동 방정식을 공식화할 필요가 없습니다.실제로 ^[9]에 나타나듯이 전자 2차파 방정식의 매우 일반적인 형태라도 방향성 성분으로 분해할 수 있어 포락선이 아닌 필드 자체에 대한 단일 1차파 방정식에 접근할 수 있다.이는 파장 스케일에서 필드 진화가 느리고 펄스의 대역폭이 전혀 제한되지 않는다는 가정만을 필요로 합니다.^[10]

고조파

비선형 매체에서 고조파 발생을 통해 고에너지 초단펄스를 발생시킬 수 있다.고강도 초단파 펄스는 매체에 고조파 배열을 생성합니다. 그런 다음 특정 관심 고조파를 흑백기로 선택합니다.이 기술은 근적외선 Ti-sapshire 레이저 펄스에서 극자외선 및 연X선 영역에서 초단파 펄스를 생성하는 데 사용되어 왔습니다.

적용들

고급 재료 3D 마이크로/나노 가공

펨토초 레이저가 다양한 응용 분야에서 복잡한 구조와 장치를 효율적으로 제작하는 능력은 지난 10년 동안 광범위하게 연구되어 왔습니다.초단파 광펄스를 가진 최첨단 레이저 가공 기술을 사용하여 서브 마이크로미터 분해능의 재료를 구조화할 수 있습니다.적절한 포토 레지스트 및 기타 투명 매체의 직접 레이저 쓰기(DLW)를 사용하면 복잡한 3차원 포토닉 결정(PhC), 마이크로 광학 컴포넌트, 그레이팅, 조직 엔지니어링(TE) 발판 및 광도파관을 만들 수 있습니다.이러한 구조는 더욱 정교한 미니어처 부품의 제작에 의존하는 통신 및 바이오 엔지니어링의 차세대 애플리케이션을 지원하는 데 잠재적으로 유용합니다.고속 레이저 가공의 정밀도, 제조 속도, 다재다능성을 갖추고 있어 제조에 필수적인 산업용 도구가 됩니다.^[11]

마이크로머신

펨토초 레이저의 응용 중에서 임플란트 표면의 미세 텍스쳐화는 지르코니아 치과 임플란트 주변의 뼈 형성을 강화하기 위해 실험되었다.이 기술은 매우 낮은 열 손상과 표면 오염물질 감소로 정밀함을 입증했습니다.사후 동물 연구는 산소층의 증가와 펨토초 레이저에 의한 미세 텍스처링에 의해 생성된 미세 및 나노 특징의 증가가 뼈 형성 속도를 높이고 골밀도를 높였으며 기계적 ^[12]^[13]^[14]안정성을 향상시켰다는 것을 보여주었다.

「」를 참조해 주세요.

Attosecond 크로노스코프
대역폭 제한 펄스
펨토케미스트리
주파수 빗
의료 이미지:초단파 레이저 펄스는 다광자 형광 현미경에 사용된다.
광통신(울트라쇼트 펄스) 필터링 및 펄스 쉐이핑.
테라헤르츠(T-ray) 생성 및 검출.
초고속 레이저 분광법
웨이브 패킷

레퍼런스

^ Paschotta, Rüdiger. "Encyclopedia of Laser Physics and Technology - ultrashort pulses, femtosecond, laser". www.rp-photonics.com.
^ J. C. Diels, Femtosecond 염료 레이저, 염료 레이저 원칙, F. J. Duarte 및 L. W. Hillman (Eds.) (학술, 뉴욕, 1990) 제3장
^ Comin, Alberto; Rhodes, Michelle; Ciesielski, Richard; Trebino, Rick; Hartschuh, Achim (2015). "Pulse Characterization in Ultrafast Microscopy: a Comparison of FROG, MIIPS and G-MIIPS". Cleo: 2015. pp. SW1H.5. doi:10.1364/CLEO_SI.2015.SW1H.5. ISBN 978-1-55752-968-8. S2CID 23655339.
^ Loriot, Vincent; Gitzinger, Gregory; Forget, Nicolas (2013). "Self-referenced characterization of femtosecond laser pulses by chirp scan". Optics Express. 21 (21): 24879–93. Bibcode:2013OExpr..2124879L. doi:10.1364/OE.21.024879. ISSN 1094-4087. PMID 24150331.
^ Band, Y. B.; Trippenbach, Marek (1996). "Optical Wave-Packet Propagation in Nonisotropic Media". Physical Review Letters. 76 (9): 1457–1460. Bibcode:1996PhRvL..76.1457B. doi:10.1103/PhysRevLett.76.1457. PMID 10061728.
^ Radzewicz, C.; Krasinski, J. S.; La Grone, M. J.; Trippenbach, M.; Band, Y. B. (1997). "Interferometric measurement of femtosecond wave-packet tilting in rutile crystal". Journal of the Optical Society of America B. 14 (2): 420. Bibcode:1997JOSAB..14..420R. doi:10.1364/JOSAB.14.000420.
^ Trippenbach, Marek; Scott, T. C.; Band, Y. B. (1997). "Near-field and far-field propagation of beams and pulses in dispersive media" (PDF). Optics Letters. 22 (9): 579–81. Bibcode:1997OptL...22..579T. doi:10.1364/OL.22.000579. PMID 18185596.
^ Trippenbach, Marek; Band, Y. B. (1997). "Dynamics of short-pulse splitting in dispersive nonlinear media". Physical Review A. 56 (5): 4242–4253. Bibcode:1997PhRvA..56.4242T. doi:10.1103/PhysRevA.56.4242.
^ Kinsler, Paul (2010). "Optical pulse propagation with minimal approximations". Physical Review A. 81 (1): 013819. arXiv:0810.5689. Bibcode:2010PhRvA..81a3819K. doi:10.1103/PhysRevA.81.013819. ISSN 1050-2947.
^ Genty, G.; Kinsler, P.; Kibler, B.; Dudley, J. M. (2007). "Nonlinear envelope equation modeling of sub-cycle dynamics and harmonic generation in nonlinear waveguides". Optics Express. 15 (9): 5382–7. Bibcode:2007OExpr..15.5382G. doi:10.1364/OE.15.005382. ISSN 1094-4087. PMID 19532792.
^ Malinauskas, Mangirdas; Žukauskas, Albertas; Hasegawa, Satoshi; Hayasaki, Yoshio; Mizeikis, Vygantas; Buividas, Ričardas; Juodkazis, Saulius (2016). "Ultrafast laser processing of materials: from science to industry". Light: Science & Applications. 5 (8): e16133. Bibcode:2016LSA.....5E6133M. doi:10.1038/lsa.2016.133. ISSN 2047-7538. PMC 5987357. PMID 30167182.
^ Delgado-Ruíz, R. A.; Calvo-Guirado, J. L.; Moreno, P.; Guardia, J.; Gomez-Moreno, G.; Mate-Sánchez, J. E.; Ramirez-Fernández, P.; Chiva, F. (2011). "Femtosecond laser microstructuring of zirconia dental implants". Journal of Biomedical Materials Research Part B: Applied Biomaterials. 96B (1): 91–100. doi:10.1002/jbm.b.31743. ISSN 1552-4973. PMID 21061361.
^ Calvo Guirado et al, 2013, 2014
^ Delgado-Ruiz et al, 2014)

추가 정보

Hirlimann, C. (2004). "Pulsed Optics". In Rullière, Claude (ed.). Femtosecond Laser Pulses: Principles and Experiments (2nd ed.). New York: Springer. ISBN 0-387-01769-0.
Andrew M. Weiner (2009). Ultrafast Optics. Hoboken, NJ: Wiley. ISBN 978-0-471-41539-8.
J. C. Diels and W. Rudolph (2006). Ultrashort Laser Pulse phenomena. New York, Academic. ISBN 978-0-12-215493-5.

외부 링크

가상 펨토초 실험실 2
랜덤 매체의 단펄스 전파 애니메이션(YouTube)
초고속 레이저:Ti 기능에 대한 애니메이션 가이드:사파이어 레이저와 증폭기.

[1] Paschotta, Rüdiger. "Encyclopedia of Laser Physics and Technology - ultrashort pulses, femtosecond, laser". www.rp-photonics.com.

[2] J. C. Diels, Femtosecond 염료 레이저, 염료 레이저 원칙, F. J. Duarte 및 L. W. Hillman (Eds.) (학술, 뉴욕, 1990) 제3장

[CominRhodes2015-3] Comin, Alberto; Rhodes, Michelle; Ciesielski, Richard; Trebino, Rick; Hartschuh, Achim (2015). "Pulse Characterization in Ultrafast Microscopy: a Comparison of FROG, MIIPS and G-MIIPS". Cleo: 2015. pp. SW1H.5. doi:10.1364/CLEO_SI.2015.SW1H.5. ISBN 978-1-55752-968-8. S2CID 23655339.

[LoriotGitzinger2013-4] Loriot, Vincent; Gitzinger, Gregory; Forget, Nicolas (2013). "Self-referenced characterization of femtosecond laser pulses by chirp scan". Optics Express. 21 (21): 24879–93. Bibcode:2013OExpr..2124879L. doi:10.1364/OE.21.024879. ISSN 1094-4087. PMID 24150331.

[5] Band, Y. B.; Trippenbach, Marek (1996). "Optical Wave-Packet Propagation in Nonisotropic Media". Physical Review Letters. 76 (9): 1457–1460. Bibcode:1996PhRvL..76.1457B. doi:10.1103/PhysRevLett.76.1457. PMID 10061728.

[6] Radzewicz, C.; Krasinski, J. S.; La Grone, M. J.; Trippenbach, M.; Band, Y. B. (1997). "Interferometric measurement of femtosecond wave-packet tilting in rutile crystal". Journal of the Optical Society of America B. 14 (2): 420. Bibcode:1997JOSAB..14..420R. doi:10.1364/JOSAB.14.000420.

[7] Trippenbach, Marek; Scott, T. C.; Band, Y. B. (1997). "Near-field and far-field propagation of beams and pulses in dispersive media" (PDF). Optics Letters. 22 (9): 579–81. Bibcode:1997OptL...22..579T. doi:10.1364/OL.22.000579. PMID 18185596.

[8] Trippenbach, Marek; Band, Y. B. (1997). "Dynamics of short-pulse splitting in dispersive nonlinear media". Physical Review A. 56 (5): 4242–4253. Bibcode:1997PhRvA..56.4242T. doi:10.1103/PhysRevA.56.4242.

[kinsler2010-9] Kinsler, Paul (2010). "Optical pulse propagation with minimal approximations". Physical Review A. 81 (1): 013819. arXiv:0810.5689. Bibcode:2010PhRvA..81a3819K. doi:10.1103/PhysRevA.81.013819. ISSN 1050-2947.

[genty2007-10] Genty, G.; Kinsler, P.; Kibler, B.; Dudley, J. M. (2007). "Nonlinear envelope equation modeling of sub-cycle dynamics and harmonic generation in nonlinear waveguides". Optics Express. 15 (9): 5382–7. Bibcode:2007OExpr..15.5382G. doi:10.1364/OE.15.005382. ISSN 1094-4087. PMID 19532792.

[MalinauskasŽukauskas2016-11] Malinauskas, Mangirdas; Žukauskas, Albertas; Hasegawa, Satoshi; Hayasaki, Yoshio; Mizeikis, Vygantas; Buividas, Ričardas; Juodkazis, Saulius (2016). "Ultrafast laser processing of materials: from science to industry". Light: Science & Applications. 5 (8): e16133. Bibcode:2016LSA.....5E6133M. doi:10.1038/lsa.2016.133. ISSN 2047-7538. PMC 5987357. PMID 30167182.

[Delgado-RuízCalvo-Guirado2011-12] Delgado-Ruíz, R. A.; Calvo-Guirado, J. L.; Moreno, P.; Guardia, J.; Gomez-Moreno, G.; Mate-Sánchez, J. E.; Ramirez-Fernández, P.; Chiva, F. (2011). "Femtosecond laser microstructuring of zirconia dental implants". Journal of Biomedical Materials Research Part B: Applied Biomaterials. 96B (1): 91–100. doi:10.1002/jbm.b.31743. ISSN 1552-4973. PMID 21061361.

[13] Calvo Guirado et al, 2013, 2014

[14] Delgado-Ruiz et al, 2014)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

Search

초단파 펄스

네임스페이스

더

목차

정의.

배경

펄스 형상 제어

측정 기술

비등방성 미디어에서의 웨이브 패킷 전파

고조파

적용들

고급 재료 3D 마이크로/나노 가공

마이크로머신

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

초단파 펄스

정의.

배경

펄스 형상 제어

측정 기술

비등방성 미디어에서의 웨이브 패킷 전파

고조파

적용들

고급 재료 3D 마이크로/나노 가공

마이크로머신

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.