포텐셜 웰

일반적인 전위 에너지 유정.

잠재적 우물은 국소 최소의 잠재적 에너지를 둘러싼 지역이다. 전위 우물에서 포획된 에너지는 전위 유정의 국부적 최소치에서 포획되기 때문에 다른 유형의 에너지(중력 전위 유정의 경우 운동 에너지)로 변환할 수 없다. 따라서 엔트로피로 인해 자연적으로 발생하는 경향이 있기 때문에, 신체는 전지구적 최소의 잠재적 에너지로 진행되지 않을 수 있다.

개요

에너지는 시스템에 충분한 에너지가 추가되어 국부 최대값이 초과될 경우 잠재 우물에서 방출될 수 있다. 양자물리학에서, 잠재적 에너지는 양자 입자의 확률론적 특성 때문에 추가 에너지 없이 잠재적 우물을 탈출할 수 있다. 이러한 경우 입자는 잠재적 우물의 벽을 통해 터널을 뚫는 것을 상상할 수 있다.

2D 전위 에너지 함수의 그래프는 언덕과 계곡의 풍경 속에서 지구 표면으로 상상할 수 있는 잠재적 에너지 표면이다. 그러면 잠재적 우물은 높은 지형을 가진 사방으로 둘러싸인 계곡이 될 것이고, 따라서 물은 다른 최소한도로 흐르지 않고 물로 채워질 수 있다(예: 호수가 될 수 있다).

중력의 경우 질량의 밀도가 너무 낮아 다른 질량의 조석력이 신체 자체의 중력보다 크지 않는 한 질량 주위의 영역은 중력 전위 우물이다.

잠재적 언덕은 잠재된 우물과는 반대편이며, 지역 최대값을 둘러싼 지역이다.

양자 구속

양자 구속은 물질의 광학적, 전자적 특성과 밀접하게 관련되는 현상인 에너지 상태와 대역격차의 증가의 원인이 된다.

물질의 직경이 전자파 함수의 드 브로글리 파장과 동일한 크기일 때 양자 구속을 관찰할 수 있다.^[1] 재료가 이렇게 작을 때, 전자적 및 광학적 특성은 벌크 재료의 특성과 크게 다르다.^[2]

입자는 입자의 파장에 비해 구속되는 치수가 클 때 마치 자유분방한 것처럼 행동한다. 이 상태에서는 연속적인 에너지 상태로 인해 밴드갭이 원래의 에너지를 유지한다. 그러나 일반적으로 나노스케일에서 구속 치수가 감소하고 일정한 한계에 도달하면 에너지 스펙트럼이 분리된다. 그 결과 밴드갭은 규모에 의존하게 된다. 입자의 크기가 줄어들면 전자와 전자구멍이 가까워지고, 이를 활성화하는 데 필요한 에너지가 증가하여 결국 빛 방출에 블루시프트가 발생한다.

구체적으로는 electron Bohr반경이라고 하는 임계 양자 측정에 접근하는 차원으로 전자와 전자구멍이 압착되어 생기는 현상을 그 효과로 설명한다. 현재 적용에서 작은 구체와 같은 양자점은 3차원으로, 양자선은 2차원으로, 양자우물은 1차원으로만 한정된다. 이들은 각각 0, 1차원, 2차원 전위 유정이라고도 한다. 이러한 경우, 제한된 입자가 자유 전달체로 작용할 수 있는 치수의 수를 가리킨다. 생명공학 및 태양전지 기술의 적용 예는 아래 외부 링크를 참조하십시오.

양자역학 보기

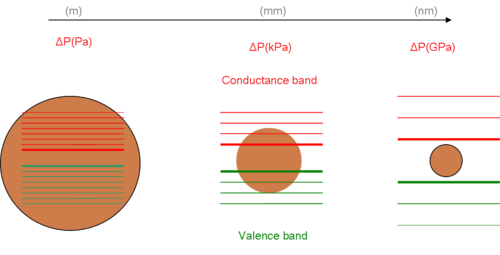
재료의 전자적, 광학적 성질은 크기와 모양에 영향을 받는다. 양자점을 포함한 잘 확립된 기술적 성과는 양자 구속 효과에 대한 이론적 확증 때문에 크기 조작과 조사로부터 도출되었다.^[3] 그 이론의 주요 부분은 익시톤이 원자의 주변 공간이 짧아짐에 따라 원자의 그것과 유사한 행동을 보인다는 것이다. 익시턴의 행동에 대한 꽤 좋은 근사치는 상자 안의 입자의 3-D 모델이다.^[4] 이 문제의 해결책은 에너지 상태와 공간의 차원 사이의 유일한^{[clarification needed]} 수학적 연관성을 제공한다. 사용 가능한 공간의 부피나 치수를 줄이면 주의 에너지가 증가한다. 도표에는 나노물질과 그것의 벌크상태 사이의 전자 에너지 수준과 밴드갭의 변화가 나타나 있다.

다음 방정식은 에너지 수준과 치수 간격 사이의 관계를 보여준다.

\psi _{n_{x},n_{y},n_{z}}={\sqrt {\frac {8}{L_{x}L_{y}L_{z}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\오른쪽)\sin \left({\frac {n_{z}\pi z}{L_{z}}\오른쪽)

E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}+\left({\frac {n_{z}}{L_{z}}}\right)^{2}\right]

연구 결과는^[5] 나노스케일의 성질 변화에 대한 대체적인 설명을 제공한다. 벌크 페이즈에서 표면은 거시적으로 관찰된 특성 중 일부를 제어하는 것처럼 보인다. 그러나 나노입자에서는 표면 분자가 우주에서 예상되는 구성에^[which?] 따르지 않는다. 그 결과 표면 장력은 엄청나게 변화한다.

고전역학관

고전적인 기계공학적 설명은 압력 강하가 규모에서 규모로 어떻게 진전되는지에 대한 증거를 제공하기 위해 영-라플라스 법칙을 채택하고 있다.

Young-Laplace 방정식은 표면 분자에 가해지는 힘의 척도 조사의 배경을 제공할 수 있다.

{\begin{aigned}\Delta P&=\gamma \nabla \cdla \cdla {\n}\&=2\gamma H\\&=\lt;leflt({R_{1}}}}+{R_{2}}}\오른쪽)\end}}}}

구형 형상 $R_{1}=R_{2}=R$ $R_{1}=R_{2}=R$ = $R_{1}=R_{2}=R$ $R_{1}=R_{2}=R$ = R $R_{1}=R_{2}=R$ 을(를) 가정하고 $R_{1}=R_{2}=R$ 새로운 반지름 $R$ ${\displaystyle$ R $}($ nm)에 대한 영-라플라스 방정식을 해결하면 새로운 $\Delta P$ $\Delta P$ ${\delta P}($ GPA $\Delta P$ 를 추정한다. 반지름이 작을수록 압력이 커진다. 나노 크기의 압력 증가는 입자 내부를 향한 강한 힘을 낳는다. 결과적으로, 입자의 분자 구조는 특히 표면에서 벌크 모드와 다른 것으로 보인다. 표면의 이러한 이상들은 원자간 상호작용과 밴드갭의 변화에 책임이 있다.^[6]^[7]

참고 항목

참조

^ M. Cahay (2001). Quantum Confinement VI: Nanostructured Materials and Devices : Proceedings of the International Symposium. The Electrochemical Society. ISBN 978-1-56677-352-2. Retrieved 19 June 2012.
^ Hartmut Haug; Stephan W. Koch (1994). Quantum Theory of the Optical and Electronic Properties of Semiconductors. World Scientific. ISBN 978-981-02-2002-0. Retrieved 19 June 2012.
^ Norris, DJ; Bawendi, MG (1996). "Measurement and assignment of the size-dependent optical spectrum in CdSe quantum dots". Physical Review B. 53 (24): 16338–16346. Bibcode:1996PhRvB..5316338N. doi:10.1103/PhysRevB.53.16338. PMID 9983472.
^ Brus, L. E. (1983). "A simple model for the ionization potential, electron affinity, and aqueous redox potentials of small semiconductor crystallites". The Journal of Chemical Physics. 79 (11): 5566. Bibcode:1983JChPh..79.5566B. doi:10.1063/1.445676.
^ Kunz, A B; Weidman, R S; Collins, T C (1981). "Pressure-induced modifications of the energy band structure of crystalline CdS". Journal of Physics C: Solid State Physics. 14 (20): L581. Bibcode:1981JPhC...14L.581K. doi:10.1088/0022-3719/14/20/004.
^ H. Kurisu; T. Tanaka; T. Karasawa; T. Komatsu (1993). "Pressure induced quantum confined excitons in layered metal triiodide crystals". Jpn. J. Appl. Phys. 32 (Supplement 32–1): 285–287. Bibcode:1993JJAPS..32..285K. doi:10.7567/jjaps.32s1.285.^{[영구적 데드링크]}
^ Lee, Chieh-Ju; Mizel, Ari; Banin, Uri; Cohen, Marvin L.; Alivisatos, A. Paul (2000). "Observation of pressure-induced direct-to-indirect band gap transition in InP nanocrystals". The Journal of Chemical Physics. 113 (5): 2016. Bibcode:2000JChPh.113.2016L. doi:10.1063/1.482008.

외부 링크

Buhro WE, Colvin VL (2003). "Semiconductor nanocrystals: Shape matters". Nat Mater. 2 (3): 138–9. Bibcode:2003NatMa...2..138B. doi:10.1038/nmat844. PMID 12612665.
반도체 기본
고체의 밴드 이론
양자점합성
생물학적 응용

[1] M. Cahay (2001). Quantum Confinement VI: Nanostructured Materials and Devices : Proceedings of the International Symposium. The Electrochemical Society. ISBN 978-1-56677-352-2. Retrieved 19 June 2012.

[2] Hartmut Haug; Stephan W. Koch (1994). Quantum Theory of the Optical and Electronic Properties of Semiconductors. World Scientific. ISBN 978-981-02-2002-0. Retrieved 19 June 2012.

[3] Norris, DJ; Bawendi, MG (1996). "Measurement and assignment of the size-dependent optical spectrum in CdSe quantum dots". Physical Review B. 53 (24): 16338–16346. Bibcode:1996PhRvB..5316338N. doi:10.1103/PhysRevB.53.16338. PMID 9983472.

[4] Brus, L. E. (1983). "A simple model for the ionization potential, electron affinity, and aqueous redox potentials of small semiconductor crystallites". The Journal of Chemical Physics. 79 (11): 5566. Bibcode:1983JChPh..79.5566B. doi:10.1063/1.445676.

[5] Kunz, A B; Weidman, R S; Collins, T C (1981). "Pressure-induced modifications of the energy band structure of crystalline CdS". Journal of Physics C: Solid State Physics. 14 (20): L581. Bibcode:1981JPhC...14L.581K. doi:10.1088/0022-3719/14/20/004.

[6] H. Kurisu; T. Tanaka; T. Karasawa; T. Komatsu (1993). "Pressure induced quantum confined excitons in layered metal triiodide crystals". Jpn. J. Appl. Phys. 32 (Supplement 32–1): 285–287. Bibcode:1993JJAPS..32..285K. doi:10.7567/jjaps.32s1.285.^{[영구적 데드링크]}

[7] Lee, Chieh-Ju; Mizel, Ari; Banin, Uri; Cohen, Marvin L.; Alivisatos, A. Paul (2000). "Observation of pressure-induced direct-to-indirect band gap transition in InP nanocrystals". The Journal of Chemical Physics. 113 (5): 2016. Bibcode:2000JChPh.113.2016L. doi:10.1063/1.482008.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Search